
2306
.pdf
Просадочность грунта при замачивании объясняется рядом причин, основная из которых – потеря неводостойких связей между частицами грунта и разрушение макропористой текстуры. Это сопровождается резкой потерей прочности грунта и быстро развивающимися деформациями уплотнения – просадками.
2.3.4. Определение модуля деформации грунта
Модуль общей деформации учитывает упругие и остаточные деформации грунта и используется для расчета осадок грунтовых оснований. Модуль деформации можно определить по данным компрессионных испытаний и по данным испытания штампом грунта статической нагрузкой в шурфе или скважине.
Определение модуля деформации по данным компрессионных испытаний. Ранее было рассмотрено, что в случае сжатия грунта без возможности бокового расширения (см. рис. 2.4) напряжениеx y z. Относительная вертикальная деформация
|
|
|
|
|
|
|
|
|
|
z |
Si |
h |
m p, |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
||||||
где m – коэффициент относительной сжимаемости, m |
|
; m |
|
– |
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
0 |
|
|
|||
коэффициент сжимаемости (2.9), отсюда |
|
|
|
0 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
m0 p |
. |
|
|
|
(2.12) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 e |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительные вертикальные деформации по закону Гука |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
1 |
|
|
z |
|
|
|
x |
|
y |
, |
(2.13) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где E0– модуль деформации; – коэффициент Пуассона. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Используя формулу |
(2.4) |
|
и |
|
|
учитывая, что z p, получаем |
||||||||||||||||||||||||||
|
|
|
1 |
р |
2р |
|
р |
|
|
|
2 |
2 |
|
|
. |
Если |
обозначить |
|
1 2 |
2 |
|
, |
||||||||||||
|
z |
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
E0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
1 |
E0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
. |
|
|
|
(2.14) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приравнивая правые части (2.10) и (2.12), получим выражение модуля деформации
3
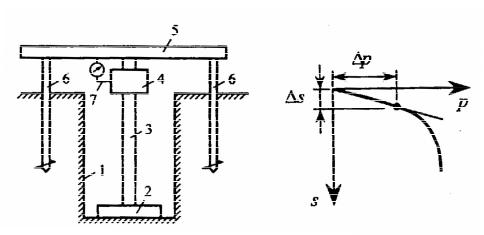
E0 |
1 e |
. |
(2.15) |
m |
|||
|
0 |
|
|
Следует отметить, что модуль деформации, определенный по данным компрессионных испытаний, часто значительно отличается от действительного, т.к. извлечение грунта из глубины для компрессионных испытаний приводит к изменению его напряженного состояния.
Определение модуля деформации по данным испытания грунта статической нагрузкой в полевых условиях. Наиболее точ-
ные значения модуля деформации получают при испытаниях грунтов в условиях их естественного залегания. Испытания проводят с помощью штампа в шурфах или в скважинах под действием статической нагрузки, передаваемой на штамп гидравлическим домкратом. Используют жесткий металлический штамп круглой формы площадью 0,5 ÷ 1 м2 (при испытаниях в шурфе) и 600 см2 (при испытаниях в скважинах). Принципиальная схема испытания грунта штампом в шурфе приведена на рис. 2.11, а.
а) |
б) |
Рис. 2.11. Испытания грунта статической нагрузкой в шурфе: а – схема установки; б – зависимость осадки от нагрузки; 1 – шурф; 2 – штамп; 3 – стойка; 4 – домкрат; 5 – упорная балка; 6 – сваи анкерной балки; 7 – измеритель деформаций
Нагрузка прикладывается ступенями и строится график зависимости осадки грунта от давления р. Модуль общей деформации определяется по формуле
E0 |
|
D p1 |
2 |
|
|
|
|
|
, |
(2.16) |
|
S |
|
||||
|
|
|
|
|
|
3

где – коэффициент, зависящий от формы штампа (для круглого = = 0,8; для квадратного = 0,9); D – диаметр штампа; p – приращение нагрузки; S – приращение осадки штампа при изменении давления на p; – коэффициент Пуассона. Формула применима в пределах линейной зависимости графика.
2.4. Водопроницаемость грунтов
Водопроницаемость – способность дисперсных грунтов пропускать (фильтровать) воду через свои поры. Ее надо учитывать при использовании грунта для возведения насыпей, при устройстве водоотводных и осушительных (дренажных) сооружений, при расчете скорости уплотнения грунта под нагрузкой и др. Движение воды через грунты является ламинарным и подчиняется закону Дарси:
Q KфAJ , |
(2.17) |
|
|
где Q – расход воды, т.е. количество воды, фильтрующейся через поперечное сечение водоносного пласта, м3/сут; Kф – коэффициент фильтрации, м/сут; А – площадь поперечного сечения потока, м2; J –
гидравлический градиент, численно равный H , здесь H – разность l
напоров, м; l – длина пути фильтрации, м.
Разделив обе части выражения (2.17) на А, получим Q KфJ .
A
Отношение Q представляет собой скорость движения воды. Следова-
A
тельно, V KфJ . При гидравлическом градиенте, равном единице,
скорость фильтрации равняется Kф. Отсюда следует, что коэффици-
ент фильтрации представляет собой скорость движения воды через грунт при гидравлическом градиенте, равном единице, и имеет размерность см/с, м/сут. Коэффициент фильтрации грунта зависит от гранулометрического и минералогического составов грунта, а также
от его |
плотности. |
Его значения изменяются для песков |
– |
|
a 10 |
1 a 10 4см/с; |
супесей – a 10 3 a 10 6 см/с; суглинков |
– |
|
a 10 |
5 |
a 10 8см/с; глин – a 10 7 a 10 10см/с, где a может быть |
||
любым |
числом. Экспериментальное определение коэффициентов |
|||
3

фильтрации грунтов проводят в лаборатории и в полевых условиях. Во всех случаях измеряют количество воды, профильтровавшейся через грунт за определенное время. Для определения коэффициента фильтрации песчаных грунтов для дорожного строительства используют фильтрационный прибор Союздорнии. Испытания проводят на образцах нарушенного сложения при максимальной плотности и оптимальной влажности по ГОСТ 22733-77.
Коэффициент фильтрации определяют расчетом по формуле
K |
ф |
Q 864 |
tAJ |
, |
(2.18) |
|
|
|
|
где Q – расход воды, см3; t – продолжительность фильтрации воды, с; 864 – переводной коэффициент из см/с в м/сут; A – площадь поперечного сечения цилиндра, см3; J – гидравлический градиент.
Найденный при испытаниях коэффициент фильтрации Kф (м/сут) приводят к его значению при температуре 10 ºС, вводя поправку
K |
10 |
K |
ф |
0,7 0,03T0 |
, |
(2.19) |
|
ф |
|
ф |
|
|
где Tф0– температура фильтрующейся воды.
2.5. Гидродинамическое давление воды
При движении потока воды в порах грунта между ним и частицами возникают объемные силы взаимодействия. Равнодействующую этих сил в каждой точке можно разложить на две составляющие: направленную вертикально вверх и действующую по направлению движущегося потока. Первая составляющая называется взвешивающей (архимедовой) силой и оказывает взвешивающее воздействие на частицы грунта (взвешивание грунта в воде). Вторая – фильтрационная сила – приводит к гидродинамическому давлению движущейся воды на частицы грунта. Взвешивающие силы обуславливают уменьшение удельного веса грунта ниже уровня подземных вод.
При фильтрации воды через поры грунта вода обтекает отдельные частицы грунта, оказывает на них давление, стремясь их сдвинуть и увлечь с собой. Это давление воды на грунтовые частицы в процессе фильтрации называется гидродинамическим давлением.
3
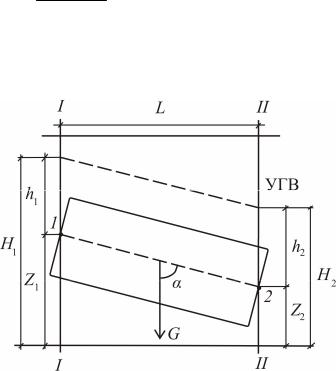
Рассмотрим схему движения воды от точки 1 к точке 2 через «грунтовый цилиндр» длиной l и площадью А (рис. 2.12). Движение воды происходит под действием гидравлического градиента
J H1 H2 . Составим уравнение проекций на ось цилиндра всех l
сил, действующих на движущуюся воду в объеме цилиндра: в точке 1 |
||
основание цилиндра испытывает давление столба воды высотой h1 и |
||
|
|
равное h1A w , где w– плот- |
|
l |
|
|
ность воды; в точке 2 основа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние |
цилиндра |
испытывает |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
давление столба воды высо- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
той h2 |
и равное |
h2A w ; |
G– |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вес |
воды |
в |
цилиндре, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G lA w , |
а проекция его на |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ось |
цилиндра – |
lA w cos . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сопротивление |
фильтрации |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
со стороны грунта равно TАl, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где T – сопротивление, отне- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сенное |
к |
единице объема |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грунта, кН/м3; Аl – объем |
||||||
|
Рис. 2.12. Схема гидродинамического |
|
|
грунтового цилиндра. |
всех |
|||||||||||||||
|
|
|
давления в скелете грунта |
|
|
|
|
|
Сумма |
|
проекций |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сил |
|
на |
|
ось |
цилиндра: |
|
h1A w h2A w Al w cos TAl. Принимая h1 H1 |
Z1; |
|
||||||||||||||||||
h |
H |
2 |
Z |
2 |
;cos |
Z1 Z2 |
, после подстановки в уравнение полу- |
|||||||||||||
|
||||||||||||||||||||
2 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
чим w H1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H2 Tl, откуда |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
H |
1 |
H |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
T |
w |
|
|
|
J w . |
|
|
(2.20) |
||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Гидродинамическое |
давление |
численно |
равно |
сопротивлению |
|||||||||||||||
давлению воды грунта, но направлено в противоположную сторону:
D J w. |
(2.21) |
Под влиянием гидродинамического давления может происходить вынос частиц из слоя водонасыщенного грунта – суффозия, выпор грунта из-под фундамента, разрыхление грунта дна котлована.
3
2.6. Прочность грунтов
Прочность грунтов – это их способность сопротивляться разрушению. В инженерно-геологических целях важно знать механическую прочность грунтов, т.е. способность сопротивляться разрушению под воздействием механических напряжений. Если деформационные характеристики определяются при напряжениях, не приводящих к разрушению (т.е. до критических), то параметры прочности грунтов определяются при нагрузках, приводящих к разрушению грунта (т.е. предельных).
Физическая природа прочности грунтов определяется силами взаимодействия между частицами, т.е. зависит от прочности структурных связей. Чем больше силы взаимодействия между частицами грунта, тем выше его прочность в целом. Установлено, что разрушение грунта происходит при сдвиге одной его части по другой под действием касательных напряжений от внешней нагрузки. Грунт оказывает при этом сопротивление сдвигающим усилиям: в несвязных грунтах это сопротивление внутреннего трения, а для связных грунтов, кроме того, сопротивление сил сцепления.
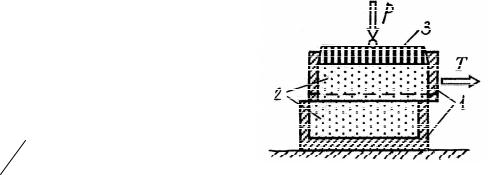
Параметры прочности чаще определяют в лабораторных условиях на одноплоскостных приборах прямого среза и стабилометрах. Схема прибора прямого среза изображена на рис. 2.13. Он представляет собой обойму из двух металлических колец, между которыми оставлен зазор (около 1 мм). Нижнее кольцо укреплено неподвижно, верхнее может смещаться горизон-  тально.
тально.
Испытания проводят на нескольких образцах, предварительно уплотненных разными вертикальными давлениями р. Величина нормального напряжения σ от нагрузки уплотнения со-
ставит p A , где A – площадь об-
разца. Затем ступенями прикладываем горизонтальные нагрузки Т, под действием которых в зоне ожидаемого сдвига развиваются касательные напряже-
ния Т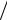 А. При некотором значении наступает предельное равновесие и происходит перемещение верхней части образца по нижней.
А. При некотором значении наступает предельное равновесие и происходит перемещение верхней части образца по нижней.
3
За предельное сопротивление грунта сдвигу принимают касательные напряжения от той ступени загружения, при которой развитие деформаций сдвига не прекращается.
При сдвиге (одноплоскостном срезе) прочность грунта зависит от соотношения нормального сжимающего и касательного сдвигающего напряжений, действующих на одной площадке: чем больше вертикальная сжимающая нагрузка на образец грунта, тем большее сдвигающее напряжение надо приложить к образцу для его среза. Взаимосвязь предельных касательных и нормальных напряженийf описывается линейным уравнением, представляющим собой уравнение предельного равновесия (закон Кулона)
tg + c, |
(2.22) |
|
|
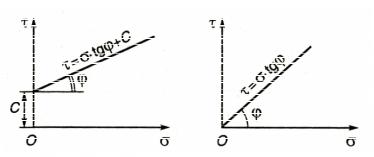
где – угол внутреннего трения, град; tg – коэффициент внутреннего трения; с – сцепление, МПа. Здесь равен углу наклона прямой в координатах f , а величина сцепления с равна отрезку, отсекаемому на оси , т.е. при 0 (рис. 2.14). Для сыпучих грунтов, не обладающих сцеплением (с = 0), закон Кулона упрощается:
tg . |
(2.23) |
|
|
а) |
б) |
Рис. 2.14. Зависимость сопротивления сдвигу связного (а) и несвязного (б) грунтов
Таким образом, и с являются параметрами прочности грунта на сдвиг.
С углом внутреннего трения в некоторых случаях отождествляется угол естественного откоса 0 , определяемый у несвязных
3
грунтов. Углом естественного откоса называется угол наклона поверхности свободно насыпанного грунта к горизонтальной плоскости. Он формируется за счет сил трения частиц.
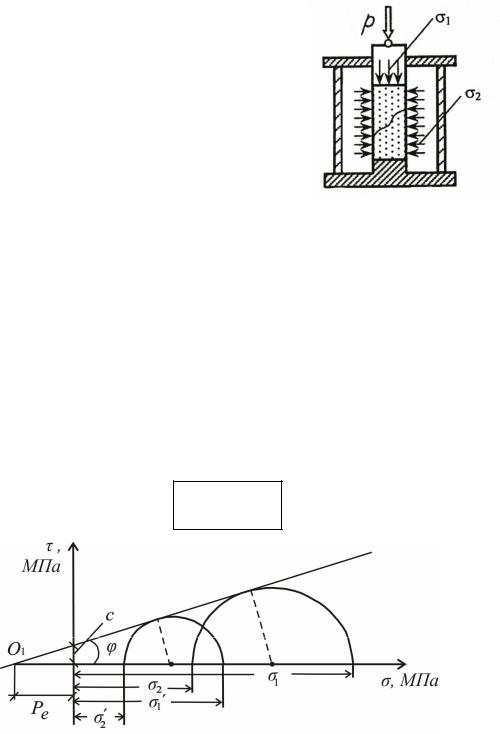
При трехосном сжатии прочность грунта зависит от соотношения главных нормальных напряжений 1 и 2. Испытания производят на приборе стабилометре (рис. 2.15). Образец грунта цилиндрической
формы заключают в водонепроницае- |
|
||
мую резиновую оболочку и вначале |
|
||
подвергают его всестороннему гидрав- |
|
||
лическому давлению, а затем к образцу |
|
||
ступенями прикладывают вертикальное |
|
||
давление, доводя образец до разруше- |
|
||
ния. Напряжения 1 |
и 2 получают из |
|
|
опыта. |
|
|
|
Испытания на |
трехосное |
сжатие |
|
проводят по такой схеме соотношения |
Рис. 2.15. Схема испытания |
||
главных напряжений, когда 1> |
2. В |
грунта в приборе трехосно- |
|
этом случае зависимость f стро- |
го сжатия (стабилометре) |
||
ится с помощью кругов Мора, радиус которых r 1 2 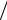 2 (рис. 2.16). Проводя испытания на трехосное сжатие грунта не менее двух образцов и построив с помощью кругов Мора предельную огибающую к ним вида f , согласно теории прочности Кулона-Мора определяют значения и с, которые в условиях трехосного сжатия являются параметрами прочности грунта.
2 (рис. 2.16). Проводя испытания на трехосное сжатие грунта не менее двух образцов и построив с помощью кругов Мора предельную огибающую к ним вида f , согласно теории прочности Кулона-Мора определяют значения и с, которые в условиях трехосного сжатия являются параметрами прочности грунта.
Давление связности (суммарно заменяющее действие сил сцепления и трения) определяется по формуле
Pe c ctg
Рис. 2.16. Круги Мора для глинистого грунта
3

Для главных напряжений условие Кулона-Мора имеет вид
sin |
1 2 |
. |
(2.24) |
|
1 2 2c ctg
2.6.1.Факторы, влияющие на сопротивление грунтов сдвигу
Главной особенностью сопротивления сдвигу несвязных грунтов является отсутствие сцепления. Поэтому сопротивление сдвигу таких грунтов характеризуется углом внутреннего трения или углом естественного откоса 0 , а основными факторами, определяющими прочность несвязных грунтов при сдвиге, будут те, которые влияют на трение между частицами грунта.
Величина сил трения между частицами несвязных грунтов прежде всего зависит от формы частиц и характера их поверхности. Окатанные частицы обусловливают снижение угла внутреннего трения грунтов за счет уменьшения сил трения и зацепления частиц. Угловатые частицы с неровной шероховатой поверхностью увеличивают угол внутреннего трения грунта как за счет зацепления, так и за счет повышения сил трения частиц.
На величину угла внутреннего трения в несвязных грунтах влияет и дисперсность. С увеличением дисперсности таких грунтов снижается за счет уменьшения сил зацепления частиц.
Среди других факторов, влияющих на сопротивление сдвигу несвязных грунтов, отметим плотность их сложения (пористость). В рыхлом сложении пористость больше и угол внутреннего трения будет меньше, чем в том же грунте плотного сложения. Наличие воды в несвязном грунте снижает трение между частицами и угол внутреннего трения. Особенностью сопротивления сдвигу связных грунтов является присутствие у них сцепления, величина которого меняется в широких пределах.
На сопротивление сдвигу связных грунтов оказывают влияние структурно-текстурные особенности (тип структурных связей, дисперсность, пористость), влажность грунтов. Связные грунты с кристаллизационными структурными связями обладают более высокими значениями с и , чем грунты с коагуляционными связями. Влияние текстуры проявляется в анизотропии прочности по разным координа-
3
там (в грунтах с ориентированной текстурой сдвиг вдоль направления ориентации частиц происходит более легко, чем поперек их ориентации).
С ростом влажности связных грунтов сцепление с и угол внутреннего трения закономерно снижаются за счет ослабления структурных связей и смазывающего действия воды на контактах частиц.
2.6.2. Нормативные и расчетные деформационные и прочностные характеристики грунтов
Грунты в основании фундаментов неоднородны. Поэтому определение какой-либо его характеристики по исследованию одного образца дает только частное значение. Для определения нормативных характеристик грунта проводят серию определения каждого показателя. Нормативные значения модуля деформации грунтов определяются как среднеарифметические величины от общего числа определений:
|
1 |
n |
|
|
xn |
|
|
xi , |
(2.25) |
|
||||
|
|
n i 1 |
|
|
где n – число определений; xi– частное значение характеристики. Нормативные значения прочностных характеристик – угла внут-
реннего трения n и сцепления cn – определяются после построения графиков сопротивления грунта сдвигу. Результаты серии опытов на сдвиг аппроксимируют прямой с использованием для обработки экспериментальных данных метода наименьших квадратов. При этом число определений сопртивлений сдвигу при одном уровне нормальных напряжений должно быть не менее шести.
Нормативные значения прямой cn и n находим по формулам
|
1 |
n |
n |
n |
n |
|
|
|
|
2 |
|
|
|
|
|
||
Cn |
|
|
|
; |
(2.26) |
|||
i i |
i i i |
|||||||
|
i 1 |
i 1 |
i 1 |
i 1 |
|
|
|
|
|
1 |
|
n |
n |
|
|
|
|
|
|
|
|
|
||
tg n |
|
|
, |
(2.27) |
|||
n i i i i |
|||||||
|
|
i 1 |
i 1 |
|
|
|
|
где n – число определений сопротивления грунта сдвигу i пряжении i ;
n |
|
n |
2 |
2 |
|
|
|
n i |
i . |
||
i 1 |
|
i 1 |
|
при на-
(2.28)
3
