Глава 6.

Диагностика технических объектов.

§1. Задачи технической диагностики.

Весьма важно иметь методы и средства для оценки технического состояния объекта, т.е. определения степени удалённости оценки от предельного состояния, выявления причин нарушения работоспособности, установления вида и места возникновения повреждения и т.п.

Все эти задачи решаются методами диагностирования, применение которых позволяет получить большой экономический эффект за счёт более полного использования потенциальных возможностей т.о.

Результаты диагностирования могут быть использованы для прогнозирования надёжности объекта и для принятия решения о проведении ремонта.

Диагностические признаки:

1. Контролируются выходные параметры изделия или его узлов.

2. Контролируются повреждения, которые приводят, или могут привести к отказу изделия.

Величины износа, деформации, вакуум являются теми диагностическими признаками, по которым можно сделать вывод о техническом состоянии объекта.

В общем случае должен быть осуществлён поиск неисправностей, например методом последовательных разбиений всего множества элементов на две части.

Неисправную часть снова разбивают на две и продолжают анализ до тех пор, пока не будет обнаружено место повреждения.

3. Контроль работоспособности изделия по косвенным признакам производится в том случае, когда непосредственно измерение выходных параметров затруднено.

Косвенными диагностическими признаками могут служить: изменения температуры, наличие в смазке продуктов износа.

§2.Диагностирование сложных систем.

Для диагностической модели входным параметром X будет значение показателя качества изделия, а входным параметром некоторый диагностический параметр – диагностический сигнал .

В общем случае в векторной форме можно записать

,

где A-оператор, характеризующий те преобразования, которые необходимо осуществить с величиной Х, чтобы получить S.

По совокупности значений множества параметров судят о принадлежности объекта к тому или иному классу:

1 класс: объект работоспособен

2 класс: объект работоспособен, но требует подналадки.

3 класс: объект неработоспособен и требует ремонта.

§3. Структура системы диагностирования.

В общем виде можно представить следующую структурную схему диагностики технических элементов:

Датчики (преобразователи), установленные на объекте диагностирования, передают разнообразные сигналы, которые преобразуются в электрические величины и поступают в блок обработки информации и оценки состояния изделия или характера изменения его параметров.

Для всех сигналов, с которыми необходимо сравнивать поступающие диагностические сигналы, предусматривается массив допустимых эталонных значений.

В некоторых случаях, чтобы оценить техническое состояние объекта, на него подаются специальные тестовые воздействия для оценки реакции объекта диагностики.

Для повышения достоверности получаемых данных осуществляется самоконтроль путем повторного выполнения отдельных операций (повторная диагностика) и сравнение полученных данных.

§4. Диагностика технологических устройств

на основе применения формулы Байеса.

Задача ставится следующим образом: известны состояния системы, включающие нормальные и типовые состояния неисправностей и их вероятностей.

Произведены наблюдения в эксплуатации или испытания, в результате чего зафиксированы некоторые признаки.

Спрашивается, как в связи с этим изменятся (уточняться) вероятности состояния системы?

Признаки:

— нагрев

— увеличение времени разгона

— увеличение погрешности изделий (позиционирования).

Для анализа необходимы статистические сведения о частости наблюдения отдельных признаков при каждом типовом состоянии системы. Эти частости в дальнейшем рассматриваются как вероятности.

Вероятность сложного события возникновения состояния и проявления комплекса признаков, согласно теореме умножения вероятностей:

–априорная (известная) вероятность состояния D_i;

P(k/D_i) – условная вероятность возникновения комплекса признаков k;

P(k) – полная вероятность возникновения комплекса признаков в системе;

P(D_i/k) – условная вероятность состояния D_i при комплексе признаков k;

Отсюда, отбрасывая левую часть, получаем:

Состояние образуют полную группу несовместных событий, т.е. событий, из которых реализуется только одно.

Полная вероятность появления комплекса признаков k в системе равна сумме вероятностей появления этого комплекса признаков при отдельных состояниях.

Подставляя, получим формулу Байеса для вероятности некоторого состоянияD_i при комплексе признаков

Комплекс признаков рассматривается состоящим из признаков, которые полагаются независимыми.

Тогда вероятность рассматривается как вероятность сложного события, равная произведению вероятностей простых событий:

Если некоторые признаки являются зависимыми, то формула трансформируется. Например, если для состояния зависимыми являются признакии, то в формулу вместо произведенияподставляют

.

При использовании формулы, отсутствие какого-либо признака, например, , рассматривается как противоположное событие с вероятностью.

Если существует признак , встречающийся только при одном состоянии системыи не встречающийся при других, то он называетсядетерминированным.

Из предыдущей формулы следует то, что при i= P(D_i/k)=1, а при i P(D_i/k)=0

Пример 1:

Для обследуемого оборудование характерно три состояния:

- состояние D₁ – неисправности узла 1, наблюдаемые у 5% оборудования, т.е. P(D₁)=0,05;

- состояние D₂ – неисправности узла 2, наблюдаемые у 15% оборудования, т.е. P(D₂)=0,15;

- нормальное состояние D3 – наблюдаемое у 80% оборудования, т.е. P(D₃)=0,8.

- Признак 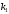наблюдается при состоянииD₁ в 20% случаев. Отсюда следует:

P(k₁/D₁)=0,2; при состоянии D₂ в 40% будет P(k₁/D₂)=0,4 и при нормальном состоянии не наблюдается.

- Признак k₂ наблюдается при состоянии D₁ в 30% случаев, ; при состояниив 50% случаев,; и при нормальном состоянии в 8% случаев,