Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Сибирский государственный автомобильно-дорожный университет (СибАДИ)»
П. А. Самосудов, В. Г. Тютнева
ПРОЕКТИРОВАНИЕ |
||||
|
|
|
|
И |
ПРОСТРАНСТВЕННЫХ |
||||
|
|
|
Д |
|
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ |
||||
|
|
А |
|
|
|
б |
|
|
|
Учебно-методическое пособие |
||||
и |
|
|
|
|
С |
|
|
|
|
Омск ♦ 2017
УДК 624.04 ББК 38.112.5 С17
Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, причиняющей вред их здоровью и развитию» данная продукция маркировке не подлежит.
Рецензенты:
д-р техн. наук, проф. Э.А. Сафронов (СибАДИ); канд. техн. наук, доц. А.Р. Нелепов (ТПО «Омскгражданпроект»)
Работа утверждена редакционно-издательским советом СибАДИ в качестве учебно-методического пособия.
Самосудов, Павел Алексеевич.
С17 Проектирование пространственных строительных конструкций [Электрон-
ный ресурс] : учебно-методическое пособие / П.А. Самосудов, В.Г. Тютнева ; кафедра «Строительные конструкции». –Электрон. дан. − О м с к : С и б АДИ, 2017. – URL: http://bek.sibadi.org/cgi-bin/irbis64r plus/cgiirbis 64 ft.exe. - Режим доступа: для авторизованных пользователей.
материала, а также вСибАДИд пломном проектировании.
ISBN 978-5-93204-885-6.
Содержится теоретическая часть программы курса, приведены примеры расчета,
конструирования пространственных и тонкостенных конструкций. Рассмотрены современные строительные системы куполообразного покрытия, арочного свода, висячих вантовых покрытий прямоугольного и круглого в плане очертания, оболочки положительной гауссовой кривизны, длинной цилиндрической оболочки, гипара.
Имеет интерактивное оглавление в виде закладок. |
||
Предназначено для |
спользован я о учающимися всех форм обучения специаль- |
|
ности «Строительство |
ун кальных зданий и |
сооружений» и направлений |
«Строительство». Может |
быть спользовано |
при самостоятельном изучении |
Текстовое (символьное) издание (4,0 МБ)
Системные требования : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ;
1 ГБ свободного места на жестком диске ; программа для чтения pdf-файлов
Adobe Acrobat Reader ; Google Chrome
Редактор И.Г. Кузнецова
Техническая подготовка − Т.И. Кукина Издание первое. Дата подписания к использованию 21.03.2017
Издательско-полиграфический комплекс СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПК СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1
© ФГБОУ ВО «СибАДИ», 2017
ВВЕДЕНИЕ
В курсовом и дипломном проектировании студентов (архитекторы бакалавриат) находят широкое применение различные интересные конструкции, отвечающие требованиям индустриальности, экологичности, имеющие современные архитектурные формы и получившие широкое применение в строительстве.
К таким конструкциям относятся купола, висячие покрытия, арочные своды, различные типы оболочек, большепролетные тонкостенные пространственные конструкции покрытия – оболочки положительной гауссовой кривизны, длинные сборные цилиндрические оболочки, гипары.
Расчет данных конструкций достаточно сложен и выполняется обычно на ЭВМ. При этом получаемая высокаяИточность результатов
расчета не всегда требуется конструктору. Вследствие этого важное
практические способы расчета
значение приобретают Д пространственных систем. Наряду с точными методами в практике проектирова-
ния оболочек существуют так называемые инженерные методы расчета, которые дают возможность достаточно быстро определить величины усилий для назначения сечений конструктивных элементов, арматуры и т. д.
лее интересных курсовыхбд пломных проектов.
Данное учебно-методическое пособие будет способствовать раз- |
|
и |
|
витию навыков расчета и конструированияА |
пространственных кон- |
струкций студентами стро тельных специальностей, выполнению бо- |
|
С |
|
Выражаем благодарность Леденёву Виктору Васильевичу и Худякову Александру Владимировичу из Государственного образова-
тельного учреждения высшего профессионального образования «Тамбовский государственный технический университет» » (ГОУ ВПО ТГТУ) за помощь в подготовке данного учебно-методического пособия.
3
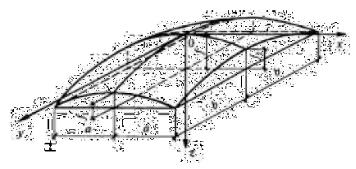
1.ОБОЛОЧКИ ПОЛОЖИТЕЛЬНОЙ ГАУССОВОЙ КРИВИЗНЫ НА ПРЯМОУГОЛЬНОМ ПЛАНЕ
1.1. Основные положения
Пологими считаются оболочки, имеющие небольшой подъём над опорным планом при
f1<a/5 и f2<b/5, |
(1) |
где 2а и 2b – размеры стороны оболочки в плане; f1 и f2 – стрелы подъёма оболочки на контуре (рис. 1).
Тип срединной поверхности характеризует форму оболочки. В качестве срединной рекомендуется принимать поверхность переноса или вращения. Образующими для всех поверхностей в практике проектирования обычно принимаются круговыеИкривые.
сборных элементов, а также условиями возведения оболочек. Члене-
Для сборных оболочек тип поверхности определяется схемой разрезки, возможностями унификацииДи удобством изготовления
ние оболочек на плиты осуществляется системой радиальных секу-
костями внутри оболочки являютсяАравновеликими, что позволяет сократить число типоразмеровис орных плит.
щих плоскостей, проходящих через ось вращения, и системой верти-
кальных плоскостей, перпендикулярных этой оси. При таком членении полосы между равноотстоящимиб радиальными секущими плос-
Оболочки по контуру оп раются на диафрагмы, которые выполняются в видеСарок, ферм ли балок, а также криволинейных брусьев, уложенных на стены ли отдельно стоящие колонны, часто расположенные по периметру здания.
В зависимости от количества и расположения ячеек здания оболочки могут проектироваться отдельно стоящими (одноволновыми) и многоволновыми в одном и двух направлениях. Многоволновые оболочки могут быть разрезными и неразрезными.
Рис. 1. Схема оболочки положительной гауссовой кривизны
4
В оболочках допускаются устройство зенитных или светоаэрационных фонарей, располагаемых в средней зоне, возможность передавать нагрузки от подвесных кранов или тельферов, пути которых крепятся к оболочкам на специальных подвесках.
1.2. Упрощённый расчёт отдельно стоящей оболочки положительной гауссовой кривизны
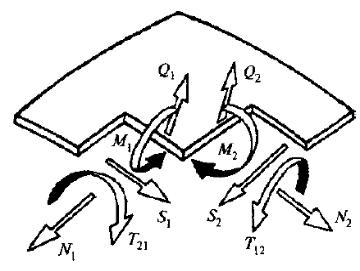
В пологой оболочке возникает система усилий: нормальные N1, N2, сдвигающая S, поперечная Q силы, а также изгибающих М1, М2 и
крутящих Т1,2, Т2,1 моментов (рис. 2).
В зависимости от степени пологости, характера нагрузки и условий опирания по контуру расчёт пологих оболочек принципиально может производиться по безмоментной теории. Безмоментная теория с учётом изгибающих моментов, возникающих в опорной зоне (краевой эффект), может быть использована в предварительных расчётах шарнирно опёртых оболочек при равномерно распределённой нагруз-
ке. |
|
|
|
|
|
И |
|
||||
|
|
|
|
|
|
|
|||||
Усилия в оболочке рекомендуется определять по формулам: |
|
||||||||||
а) нормальные силы N1 |
в направлении оси х и N2 в направлении |
||||||||||
оси у по линии у = 0: |
|
|
|
|
Д |
|
|
|
|||
|
ql |
2 |
|
|
ql |
2 |
|
|
|
(2) |
|
N1 = − |
kN ; |
N2 = − |
kN |
|
; |
||||||
δ |
|
δ |
|
2 |
|
||||||
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
А |
|
|
|
|
|
|||
б) изгибающие моменты в направлении оси х по линии у = 0: |
|
||||||||||
|
бМ = ql2–kM ; |
|
|
|
|
(3) |
|||||
и |
|
|
|
|
|
|
|
|
|||
С |
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. Схема усилий в пологих оболочках
5
в) сдвигающие усилия по граням оболочки: |
(4) |
|||||
S = − |
ql2 |
|
kS ; |
|||
|
δ |
|
|
|||
г) поперечные силы, действующие по граням оболочки: |
(5) |
|||||
Q = qlkQ ; |
||||||
д) главные усилия, действующие в оболочке в направлении диа- |
||||||
гонали и нормально к ней: |
2 |
|
(6) |
|||
N ГЛ = − |
ql |
kГЛ , |
||||
δ |
|
|
|
|||
где kN1, kN2, kМ, kS, kQ, kГЛ – коэффициенты, определяемые по прил. |
||||||
1 – 6; δ – фиктивная толщина оболочки. |
|
|||||
Односторонняя равномерно распределённая нагрузка заменяется
комбинированной из симметричной и обратно симметричной нагру- |
|
зок. |
И |
|
При обратно симметричной нагрузке моменты возникают не |
|
Д |
только на приопорных участках, но и в средней части оболочки у мест перепада нагрузок. Однако они носят условный характер, так как в
действительности резкого перепада нагрузки в средней части оболоч-
принимается, что изги ное состояниеАоболочки имеет характер краевого эффекта и быстро затухает по мере удаления от края оболочки.
ки нет. Вблизи контура оболочки возникает искажение безмоментно-
го напряжённого состояния, так как здесь действуют краевые изги-
бающие моменты и поперечные силы. Для приближённых расчётов
Зона действия изг бающ х моментов распространяется не далее |
||||||
(3...4) S от края, где |
|
б |
|
|||
|
|
|
|
|
(7) |
|
|
|
|
|
|
|
|
|
|
S |
= 0,76 Rδ . |
|||
|
и |
|
|
|
|
|
Нагрузкой на диафрагмы оболочек являются опорное давление, |
||||||
С |
|
|
|
|
|
|
передаваемое по граням в виде сдвигающих сил S, касательных к срединной поверхности оболочки, обратных по направлению и равных по величине сдвигающим усилиям в оболочке, а также поперечные силы.
При расчёте диафрагм, выполняемых в виде ферм, усилия собираются в узлы.
В оболочках с контурными элементами в виде криволинейного бруса, опёртого на колонны, растягивающие усилия воспринимаются контурными брусьями и частично оболочкой, главные усилия к углам уменьшаются, а в местах примыкания к диафрагмам возникают значительные по величине отрицательные изгибающие моменты.
6