

Министерство образования и науки Российской Федерации СибАДИФедеральное государственное бюджетное образовательное учреждение высшего образования
« ибирск й государственный автомобильно-дорожный университет (СибАДИ)»
В. . Червенчук, А. А. Руппель
ЭЛЕКТРОННЫЕ И МИКРОПРОЦЕССОРНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Учебно-методическое пособие
Омск ■ 2018

УДК 621.113.066 |
Согласно 436-ФЗ от 29.12.2010 «О защите детей |
от информации, причиняющей вред их здоровью |
|
СибАДИ |
|
БКК 39.33-04 |
и развитию» данная продукция маркировке |
Ч-45 |
не подлежит. |
Рецензенты:
канд. техн. наук, доц. Б.В. Савельев (СибАДИ); канд. техн. наук, доц. Р.Ю. Сухарев (СибАДИ)
Работа утверждена редакционноздательск м советом Си АДИ в качестве учебно-методического пособия.
Червенчук, Владимир Дм тр ев ч.
Ч-45 Электронные и микропроцессорные с стемы управления [Электронный ресурс] : учебно-методическое пособие / В.Д. Червенчук,
А.А. Руппель. – Электронные дан. – Омск : С бАДИ, 2018. – URL: http://bek.sibadi.org/cgi-bin/irbis64r plus/cgiirbis 64 ft.exe. - Режим доступа: для авторизованных пользователей.
ISBN 978-5-00113-079-6.
Рассмотрены практические вопросы применения цифровых интегральных схем транзисторно-транзисторной логики при проектировании микропроцессорных систем управления, их электронные схемы и принципы работы. Изложены методы отладки электронных схем средствами имитации работы электрических цепей.
Имеет интерактивное оглавление в виде закладок.
Предназначено для проведения практических занятий и лабораторных работ по дисциплинам «Электрические и электронные аппараты», «Проектирование микропроцессорных систем автомобилей», «Основы цифровой техники», «Электронные системы автомобилей», «Источники автономного питания транспортных средств», «Электрооборудование автомобилей и тракторов» с обучающимися всех форм обучения по направлениям бакалавриата «Энергетическое машиностроение», «Технология транспортных процессов», «Наземные транспортно-технологические средства», «Эксплуатация транспортно-технологических машин и комплексов», «Профессиональное обучение» и специалитета по специальности «Наземные транспортно-технологические комплексы».
Подготовлено на кафедре «Тепловые двигатели и автотракторное электрооборудование».
Текстовое (символьное) издание (4 МБ)
Системные требования: Intel, 3.4 GHz; 150 Мб; Windows XP/Vista/7;DVD-ROM;
1 Гб свободного места на жестком диске; программа для чтения pdf-файлов: Adobe Acrobat; Foxit Reader Редактор Н. . Косенкова
Техническая подготовка Н.В. Кенжалинова Издание первое. Дата подписания к использованию 30.05.2018
Издательско-полиграфический комплекс СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПК СибАДИ. 644080, г. Омск, ул. Поселковая, 1
© ФГБОУ ВО СибАДИ, 2018
ВВЕДЕНИЕ
Понятие электронной системы управления является более общим, нежели понятие микропроцессорной системы. Под электронной системой управления понимается система, построенная на интегральных схемах и полупроводниковых приборах. Алгоритм функционирования
такой системы однозначно определяется принципиальной электриче- СибАДИской схемой блока управления. Чтобы изменить этот алгоритм, необходимо менять весь электронный блок управления (ЭБУ) системы. Для
нового алгор тма функционирования потребуется переделка всей системы электронных схем, из которых состоит ЭБУ. Всю совокупность данных схем называют аппаратным обеспечением системы управления.
Однако если дополнить такой ЭБУ микроконтроллером (программно управляемым устройством, аналогичным компьютеру), то алгоритм функц он рования полученной системы управления можно будет менять без зменения ее аппаратных средств. Это уже будет микропроцессорная с стема управления, которая помимо аппаратных средств (hardware) удет иметь еще и программные средства (software). В м кропроцессорной системе алгоритм функционирования можно менять, не изменяя при этом hardware.
В настоящее время микропроцессорные системы имеют очень широкое применение не только в робототехнике, системах управления различными узлами и агрегатами автомобилей, но и в бытовой технике. Интегральные схемы применяются в теле- и радио-аппаратуре, измерительных и бытовых приборах, мобильных телефонах, айфонах, смартфонах, стиральных машинах, холодильниках и т.д. Трудно сегодня найти такой бытовой прибор, где бы ни использовались электронные микросхемы. Поэтому их изучение имеет не только научно-технический, но и практический интерес. Электроника как наука возникла на стыке трех наук – электродинамики, физики твердого тела и математической логики. Электронные микросхемы таят в себе большие возможности для проектирования «умных» устройств, способных рационально управлять сложными техническими системами. будущее именно за такими системами. Следовательно, усвоение азов электроники – требование времени. Целью настоящего пособия является помочь студентам усвоить эти азы. В качестве инструмента для самостоятельной работы студентов предлагается симулятор проектирования и имитации работы электронных схем Electronics Workbench, к которому имеется свободный доступ в Интернете. Методы пользования этим программным продуктом представлены в описании рекомендаций по выполнению лабораторных работ.
3
1.ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
КПРАКТИЧЕСКИМ ЗАНЯТИЯМ
Настоящее учебно-методическое пособие содержит материал к двенадцати практическим занятиям. Практические занятия проводятся аудиторно, наличие вычислительных средств желательно (задания, требующие наличия вычислительной техники, являются дополнительными и могут быть выполнены студентами во внеаудиторное время). Наличие краткого теорет ческого материала, пояснений и примеров позволяет
студенту выполн ть задания к практическим занятиям самостоятельно, |
|
что дает возможность использовать данные методические указания при |
|
заочной форме обучения. Работа рассчитана на 2 часа: час на объясне- |
|
С |
примерно час – на выполнение заданий и ответы на |
ние темы занят |
|
выполненияуспешного х тре уется наличие базовых знаний дисциплин «Электротехн ка» и «Физические основы электроники».
вопросы.
б вым темам курса поАмикропроцессорным системам, а именно к темам:
Данные практ ческие занятия относятся к первому этапу подготовки спец ал стов по электронной и микропроцессорной технике. Для
Практ ческ е занятия по тематике относятся к первым пяти базо-
«Логические функции и элементы», «Комбинационные схемы», «Триггеры и регистры», «Счетчики и сумматоры», «Запоминающие устройства и средства о мена данными между ними». Общей задачей данных занятий является проработка ряда специфических практических вопросов схемотехники логических элементов.
конъюнктивные нормальные формыД, практическое применение этих методов для синтеза логических автоматов без памяти. При этом решение
Задачей первых трёх практических занятий является закрепление
знаний по булевой алгебре и исчислению булевых функций, усвоение
методов и средств их преобразований в совершенные дизъюнктивные и
данной задачи обеспечит понимание языка электронных схем и умение составлять эти схемы по формулам булевой алгебры и таблицам истинности для этих формул.
Задачей последующих занятий являетсяИзакрепление знаний о ключевых элементах микропроцессорных систем (их наименовании, функциональном назначении и логике их работы).
Практические занятия идут по нарастанию сложности и требуют обязательной проработки теоретического лекционного материала по соответствующим темам.
Для успешного выполнения работ необходимо иметь навыки работы со справочной литературой [3, 5], изучить номенклатуру выпускаемых промышленностью изучаемых электронных компонентов в инте-
4

гральном исполнении, при необходимости уметь извлекать необходимую справочную информацию из Интернета. Желательно уметь пользоваться компьютерными средствами схемотехнического моделирования.
|
Практическое занятие №1 |
|
ЛОГИЧЕСКИЕ ОПЕРАЦИИ СОЕДИНЕНИЯ |
|
Цель занят я: усвоение методов моделирования работы комбина- |
ционных устройств логическими операциями соединения. |
|
СКратк е теорет ческие сведения |
|
|
Электрон ка дел тся на аналоговую и цифровую. Цифровую мик- |
росхему можно представить в виде «черного ящика» (мы не знаем, что |
|
там |
) с n входами и m выходами. Входные и выходные сигналы |
внутритакой м кросхемы являются цифровыми величинами, то есть величинами, которые могут меть только два возможных значения – 0 или 1. В математ ке так е вел чины называют булевыми переменными.
Микросхемы, у которых значения выходных сигналов однозначно определяются значениями входных сигналов, называются комбинацион-
ными логическими устройствами (КЛУ).
Рассмотрим простейшее КЛУ с двумя входами и одним выходом
(рис. 1.1). |
|
|
|
|
|
|
бА |
|
|
|
|||
|
x1 |
микросхема |
|
yi |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x2 |
Д |
||||
|
|
|
|
|||
|
|
Рис. 1.1. КЛУ с двумя входами |
|
|
|
|
Здесь выходом будет зависимая булева переменная yi |
f x1, x2 , то |
|||||
есть булева функция от двух булевых переменных x1 |
и |
x2 . Булевы |
||||
|
|
И |
||||
функции от двух булевых переменных называют логическими операциями соединения. Они представляют собой математические модели элементарных микросхем с двумя входами и одним выходом.
Общее число таких микросхем будет равно 222 16. Именно столько подмножеств имеет единичный квадрат, который можно рас-
сматривать как множество 0,1 2 0,0 , 0,1 , 1,0 , 1,1 [1, с. 44]. Полный перечень бинарных булевых функций представлен в таб-
лице (табл. 1.1) [1, с. 45]. В данной таблице в крайнем левом столбце
5

|
указаны булевы переменные (x1 |
и |
|
x2 ) и функции (y1, y2 , …, |
|
|
y16 ) как |
|||||||||||||||||||||||||||||
|
обозначение соответствующих строк таблицы. В строках, помеченных |
|||||||||||||||||||||||||||||||||||
|
символами |
y1,y2 , …, |
y16 , стоят нули и единицы. Единицы указывают, |
|||||||||||||||||||||||||||||||||
|
какие вершины единичного квадрата принадлежат области истинности |
|||||||||||||||||||||||||||||||||||
|
(ОИ) соответствующей функции yi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1. |
||||||||||||||||
|
|
|
Перечень всех булевых функций с числом аргументов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
№ |
0 |
1 |
|
2 |
3 |
|
Название функции |
|
|
|
|
|
|
|
Обозначение |
|
|||||||||||||||||||
|
пары |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x |
0 |
0 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
0 |
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
0 |
|
0 |
0 |
|
Константа «ложь» |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
0 |
0 |
|
0 |
1 |
|
Конъюнкция (логическое И) |
|
x & x |
|
|
|
||||||||||||||||||||||
|
y10 |
|
|
бА |
x1 |
x2 |
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
||
|
y |
3 |
0 |
0 |
|
1 |
0 |
|
Запрет (x запрещает x |
2 |
) |
|
|
|
x |
|
x |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y4 |
|
|
|
|
|
|
Пустая операция над x1 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
||||||||||||
|
y |
5 |
0 |
1 |
|
0 |
0 |
|
Запрет (x |
2 |
запрещает x ) |
|
|
|
x |
2 |
x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
y6 |
0 |
1 |
|
0 |
1 |
|
Пустая операция над x2 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
||||||||||||||
|
y |
7 |
0 |
1 |
|
1 |
0 |
|
Сложение по модулю 2 |
|
|
|
|
|
x x |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
y |
|
0 |
1 |
|
1 |
1 |
|
Дизъюнкция (логическое ИЛИ) |
|
x x |
2 |
|
|||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
y9 |
1 |
0 |
|
0 |
0 |
|
Д |
|
|
x |
|
|
|
|
|||||||||||||||||||||
|
|
|
Стрелка Пирса |
(ИЛИ-НЕ) |
|
|
x |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
0 |
|
0 |
1 |
|
Эквиваленция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y |
|
1 |
0 |
|
1 |
0 |
|
Инверсия x |
2 |
(НЕ x |
2 |
) |
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|||||||
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
1 |
0 |
|
1 |
1 |
|
Импликация (x |
2 |
влечетx ) |
|
|
x |
2 |
x |
|
|||||||||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||||||||||||||||||
|
y |
|
1 |
1 |
|
0 |
0 |
|
Инверсия x (НЕ x ) |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
13 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
y |
|
1 |
1 |
|
0 |
1 |
|
Импликация (x влечетx |
2 |
) |
|
x |
|
x |
2 |
|
|||||||||||||||||||
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
|
1 |
1 |
|
1 |
0 |
|
Штрих Шеффера ( -НЕ) |
|
|
x |
|
|
|
|
x |
|
|
|
|
|
||||||||||||||
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y |
|
1 |
1 |
|
1 |
1 |
|
Константа «истина» |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ связей между логическими операциями соединения
Поскольку строка y1 содержит одни нули, то область истинности данной функции (константы «ложь») – пустое множество. В строке y2
Чарлз Сандерс Пирс (1839 – 1914) – амер. математик и логик. Родоначальник американского прагматизма.
6
только одна единица, соответствующая вершине 1,1 с номером 3 еди-
ничного квадрата 0,1 2 , и, следовательно, областью истинности для конъюнкции будет подмножество 1,1 .
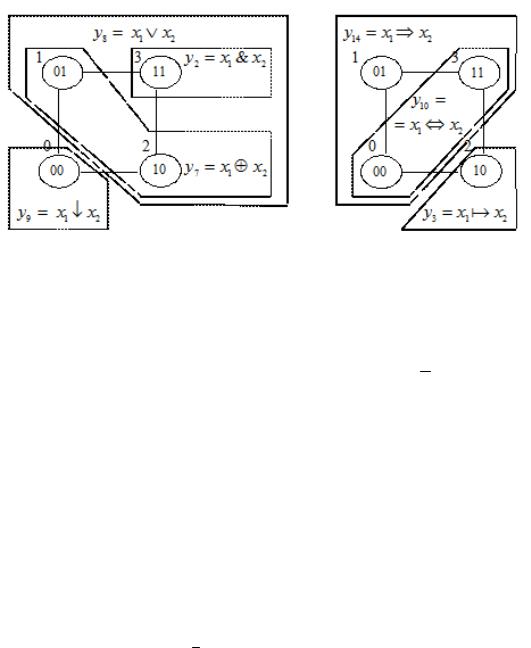
На рис. 1.2 и 1.3 показаны границы областей истинности для конъюнкции, сложения по модулю 2, дизъюнкции, стрелки Пирса, им-
С |
|
|
|
|
|
|
|
пликации x1 x2 , эквиваленции и запрета x1 x2 (сравните выделен- |
|||||||
ные области с соответствующими строками y2 , y7 , y8, y9 , y14 , y10 , y3 |
|||||||
нашей |
табл цы). |
Здесь |
|
единичный |
квадрат |
||
0,1 2 |
0,0 , 0,1, 1,0 , 1,1 в качестве примера разбит семью спо- |
||||||
собами |
|
|
|
|
|
|
|
|
на два подмножества. |
|
|
|
|
|
|
Рис. 1.2. ОИ функций: y2,y7 |
,y8,y9 |
Рис. 1.3. ОИ функций: y3,y10,y14 |
|||||
СобственнобАбинарных функций в табл. 1.1 только десять, т.к. y1 и |
|||||||
y16 логические константы (0 и 1), а y4 , |
y6 , y11 и y13 унарные функции, |
||||||
т.е. функции одной переменной, из которых практический интерес |
|||||||
представляет лишь одна унарная булева функция y |
x |
, называемая ин- |
|||||
версией (отрицанием) переменнойД. |
|
||||||
Итак, в качестве простейших булевых функций мы получили две |
|||||||
логические константы, одну унарную и десять бинарных функций. Ни- |
|||||||
же покажем, что изначальных булевых функций, из которых строятся |
|||||||
все остальные, гораздо меньше. |
|
|
|
|
|
||
Полученные выше логические операцииИсоединения можно выра- |
|||||||
зить через три основные булевы функции: инверсию, конъюнкцию и |
|||||||
дизъюнкцию, т.е. через те |
логические |
операции, которыми |
обычно |
||||
пользуются при составлении сложных условий. Тогда все остальные логические операции соединения выразятся в виде формул с использованием лишь операций инверсии, конъюнкции и дизъюнкции
yi Fi( ,&, ) Fi(НЕ,И,ИЛИ). (1.1)
7
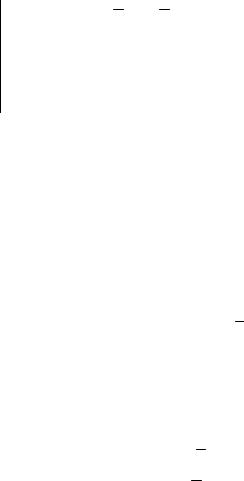
Из табл. 1.1 следуют правила отрицания (инверсии), логического умножения (конъюнкции) и логического сложения (дизъюнкции), которые можно представить отдельной таблицей.
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.2 |
|
|
|
Таблица истинности основных булевых функций |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
|
x1 |
|
|
x |
2 |
|
x1 & x2 |
|
x1 x2 |
|
||
|
|
x1 |
|
|
|
|
|
|
|
||||||
|
|
1 |
|
1 |
0 |
|
0 |
|
1 |
|
1 |
|
|||
|
|
1 |
|
0 |
0 |
|
1 |
|
0 |
|
1 |
|
|||
|
|
0 |
|
1 |
1 |
|
0 |
|
0 |
|
1 |
|
|||
компози |
ц |
ию |
|
1 |
|
0 |
|
0 |
|
||||||
|
|
0 |
|
0 |
1 |
|
|
|
|
||||||
Подставляя в конъюнкции вместо переменной |
x2 ее инверсию |
||||||||||||||
(осуществляя |
|
|
|
|
|
конъюнкции и инверсии), |
получим новую |
||||||||
булеву функц ю x1 & x2 . Согласно табл. 1.2 областью истинности дан- |
|||||||||||||||
ной функц |
удет множество |
1,0 . Только на вершине 1,0 эта |
|||||||||||||
функц я меет значение единицы, а на всех остальных вершинах единичного квадрата она о ращается в нуль. Но ту же область истинности
имеет и запрет x1 x2 , т.е. данные функции одно и то же. Поэтому |
|
y3=x1 x2 =x1 & x2 . |
(1.2) |
Иначе говоря, мы выразили функцию y3 через конъюнкцию и ин-
версию формулой (1.2). налогично можно выразить и другие булевы |
||||
Д |
|
|||
функции, область истинности которых содержит только одну вершину |
||||
единичногобквадрата. ПолучимА |
|
|||
y5=x2 x1= |
x1 & x2 , |
(1.3) |
||
y9 =x1 x2 = |
x1 & x2 . |
|
(1.4) |
|
Основные результаты анализа |
И |
|||
|
|
|||
Замечание 1. Из полученных результатов следует очень простое правило получения формул, использующих операции инверсии и конъюнкции, для аналитического выражения булевых функций с областью истинности из одной вершины единичного квадрата. Формула эта строится по координатам той самой вершины – единица заменяется соответствующей переменной, а нуль ее инверсией, и берется их конъюнкция.
Теперь вычислим дизъюнкцию функций y3 и y5 по правилам логического сложения (см. 1-й, 2-й и последний столбцы табл. 1.2). По этим правилам будут складываться соответствующие элементы строк y3
и y5 табл. 1.1. В результате такого сложения получится строка y7 той же таблицы.
8
Замечание 2. Строка y7 определяет множество вершин, равное объединению множеств, определяемых складываемыми строками y3 и y5. Следовательно, операцию дизъюнкции булевых функций можно заменить операцией объединения их областей истинности.
Таким образом, |
установлено, что y7 y3 y5, а с учетом выраже- |
||||
ний (1.2) и (1.3) |
x1 x2 (x1 & |
x |
|
x1 & x2 ). |
|
y7 |
2 ) ( |
(1.5) |
|||
Замечан е 3. Функция y7 (сложение по модулю 2) имеет область
истинности 1,0 , 0,1 (рис. 1.2), сопоставление которой с формулой |
|||||||||||||||||||
правило |
|
||||||||||||||||||
(1.5) дает следующее правило аналитического выражения булевой |
|||||||||||||||||||
Сфункц , область |
стинности которой содержит более одной вершины. |
||||||||||||||||||
начала находятся формулы для каждой из вершин области истинности |
|||||||||||||||||||
по прав лу, указанному |
|
замечании 1, а затем эти формулы соединяют- |
|||||||||||||||||
бА |
|
||||||||||||||||||
ся знаком д зъюнкц . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя это |
|
|
|
|
, найдем аналитические выражения, по- |
||||||||||||||
строенные на трех логических операциях (инверсии, конъюнкции и |
|||||||||||||||||||
дизъюнкц ), для остальных инарных булевых функций. Получим |
|||||||||||||||||||
y8 x1 x2 |
(x1 & |
x |
2 ) ( |
x1 & x2 ) (x1 & x2 ), |
(1.6) |
||||||||||||||
y10 x1 x2 |
( |
x1 & |
x |
2 ) (x1 & x2 ), |
(1.7) |
||||||||||||||
y12 x2 x1 |
( |
x1 & |
x |
2 ) (x1 & |
x |
2 ) (x1 & x2 ), |
(1.8) |
||||||||||||
y14 x1 x2 |
( |
x1 & |
x |
2 ) (x1 & x2 ) (x1 & x2 ), |
(1.9) |
||||||||||||||
|
|
|
|
|
|
|
Д |
|
|||||||||||
y15 x1 |
x2 |
|
( |
x1 & |
x |
2 ) ( |
x1 & x2 ) (x1 & |
x |
2 ). |
(1.10) |
|||||||||
Равенство (1.6) |
вызывает некоторое удивление, где дизъюнкция |
||||||||||||||||||
представлена формулой (правая часть равенства) с использованием инверсии, конъюнкции и той же дизъюнкции. Видимо существуют какието тождественные преобразования булевыхИформул, позволяющие их упрощать, что и обеспечивает возможность из более сложной формулы, стоящей справа в равенстве (1.6), получить более простую, стоящую слева от знака равно данного равенства. К этому вопросу мы еще вернемся, как только покончим с проблемой отыскания базовых булевых функций – первокирпичиков, из которых выстроен весь мир булевых функций, и, следовательно, из которых можно будет получать всё множество микросхем.
Пока же только установлено, что любая логическая операция соединения является композицией не более трех логических операций (инверсии, конъюнкции и дизъюнкции).
Еще одним важным свойством этих функций является принцип двойственности: i 1,16 j 1,16 (yi yj )&(yj yi) . Иначе гово-
9

ря, для каждой логической операции соединения существует ей противоположная, т.е. такая, у которой область истинности совпадает с областью ложности первой логической операции и, наоборот, область истинности первой логической операции совпадает с областью ложности ей противоположной операции. Это понятие противоположности распространяется на все логические функции.
Тогда противоположные функции в табл. 1.1 будут иметь строки со взаимно противоположными элементами (одна строка переходит в другую при замене в ней всех единиц на нули, а нулей на единицы. На-
пример, |
y |
8 y9, т.е. |
нверсией дизъюнкции является стрелка Пирса, что |
||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
дает еще одну формулу для определения данной функции y9 x1 x2 . |
|||||||||||||||||||
САналог чно y |
y |
|
тогда y |
x |
|
x |
|
|
|
|
|
, т.е. штрих Шеффера |
|||||||
2 |
|
2 |
x & x |
2 |
|
||||||||||||||
|
|
||||||||||||||||||
|
|
|
15 |
|
|
|
15 |
1 |
|
|
1 |
|
|
|
|
||||
выраз лся только через конъюнкцию и инверсию более простой форму- |
|||||||||||||||||||
лой, чем в выражен |
|
(1.10). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Контрольные вопросы и задания |
|||||||||||||||
1.По |
. 1.1 определите области истинности функций y5 и y15. |
||||||||||||||||||
2.Область |
А |
|
|
|
|||||||||||||||
ст нности какой функции равна объединению областей |
|||||||||||||||||||
истинности конъюнкции и сложения по модулю два? |
|||||||||||||||||||
3.Потабл. 1.1 и 1.2 найдите области истинности для функций |
|||||||||||||||||||
x1 x1 |
и x1 x1. Установите, каким булевым функциям они отве- |
||||||||||||||||||
чают. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.Определите все противоположные пары для функций табл. 1.1.
5.Каким логическим операциям соединения соответствуют форму-
лы: (x1 & x2 ) (x1 & x2 ), (x1 & x2 ) (x1 & x2 ), (x1 & x2) (x1 & x2)?
Приведите для них таблицы истинности.Д
Практическое занятиеИ№2
СОВЕШЕННЫЕ ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ. ШЕФФЕРОВЫ ФУНКЦИИ
Цель занятия: усвоение методов моделирования работы комбинационных устройств совершенными дизъюнктивными нормальными формами.
Краткие теоретические сведения
Распространим полученные результаты предыдущего параграфа на n-арные булевы функции. Функция
y f x1, x2,..., xn
10

выделяет на гиперкубе 0,1 n некоторое подмножество вершин – область истинности этой функции.
Если эта область содержит только одну вершину a a1, a2,...,an , то согласно установленному выше правилу (замечание 1.1) формулу данной функции можно построить по координатам данной вершиныa1,a2,...,an . Такая формула будет представлять конъюнкцию n булевых величин вида
f1 x1, x2,..., xn y1 & y2 &...& yn, где yi |
x |
|
при a |
1, |
|
|
|
|
|
i |
i |
(i 1, n) (1.11) |
|||
|
xi |
при ai |
0. |
||||
Эти формулы называют элементарными конъюнкциями длины n. |
||||||||
Определен е 1. Элементарная конъюнкция называется полной, ес- |
||||||||
С |
|
улевой функции (имеющей область ис- |
||||||
она является формулой для |
||||||||
тинности |
з одной только вершины гиперкуба). Длина полной элемен- |
|||||||
тарной конъюнкц |
всегда равна n размерности гиперкуба. Если дли- |
|||||||
на элементарной конъюнкции меньше n, то она называется неполной. |
||||||||
ли |
|
имеет область истинности, которая |
||||||
Пусть функц я |
fk x1, x2,..., xn |
|||||||
состо т |
з k верш н гиперку а 0,1 n . Координаты этих вершин можно |
|||||||
записать в матрице с числом строк n и числом столбцов k . |
||||||||
б1 2 ... k |
||||||||
|
|
1 |
a11 |
a12 |
... |
a1k |
|
|
|
|
2 |
a21 |
a22 |
... |
a2k |
|
|
|
|
... |
... ... ... ... |
|
|
|||
|
А |
|
|
|||||
|
|
n an1 |
an2 |
... |
ank |
|
|
|
Такую матрицу называют булевой. Каждый из ее столбцов опреде-
ляет координаты одной из вершин области истинности булевой функ- |
|||||||||||
Д |
|||||||||||
ции fk x1, x2,..., xn . Тогда, согласно замечанию 3, для данной функции |
|||||||||||
можно построить следующую формулу |
|
|
|
|
|
|
|
|
|||
fk x1, x2,..., xn (y11 & y21 &...& yn1) (y11 |
& y21 |
&...& yn1) ... |
|||||||||
x |
|
при a |
И |
||||||||
|
|
1, |
|
|
|
|
(1.12) |
||||
|
i |
|
ij |
|
|
|
|
|
|
||
(y11 & y21 &...& yn1), где yij |
|
|
при a |
|
|
(i 1, n; j 1, k) |
|||||
x |
i |
ij |
0. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Определение 2. Формула (1.12) называется совершенной дизъюнктивной нормальной формой булевой функции fk x1, x2,..., xn . Она пред-
ставляет собой дизъюнкцию всех полных конъюнкций для всех вершин области истинности этой функции.
11
Очевидно, полная конъюнкция является частным случаем совершенной д.н.ф. (подобно тому, как столбец является частным случаем матрицы). Поэтому можно утверждать, что формулу (1.12) можно по-
строить для любой булевой функции, имеющей непустую область истинности. Иначе говоря, совершенная д.н.ф. существует для любой булевой функции, кроме константы «ложь». Однако эту константу можно определить более простой формулой 0 xi & xi , использующей только две из трех основных (теперь их так уже можно называть с полным правом!) лог ческ х операций.
Сдизъюнкц я. помощью их различных композиций получаются любые друг е булевы функции. Это означает, что система из данных трех ло-
Итак, основу м роздания булевых функций могут составлять всего лишь три простейш е логические операции – инверсия, конъюнкция и
х операц й является функционально полной системой булевых
схем: НЕлюбую, И, ИЛИ, достаточно лишь соединить их выводы соответствующим образом.
функц й [1, с. 62 – 64].
На языке электронных микросхем это означает, что можно по- |
|
гическ |
|
стро ть |
КЛУ с использованием всего лишь трех типов микро- |
Примеры построения совершенных д.н.ф. по заданным облас-
тям истинности |
|
|
|
|
|
|
|
001 |
011 |
|
|||
Пример 1. Построить совершенную |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
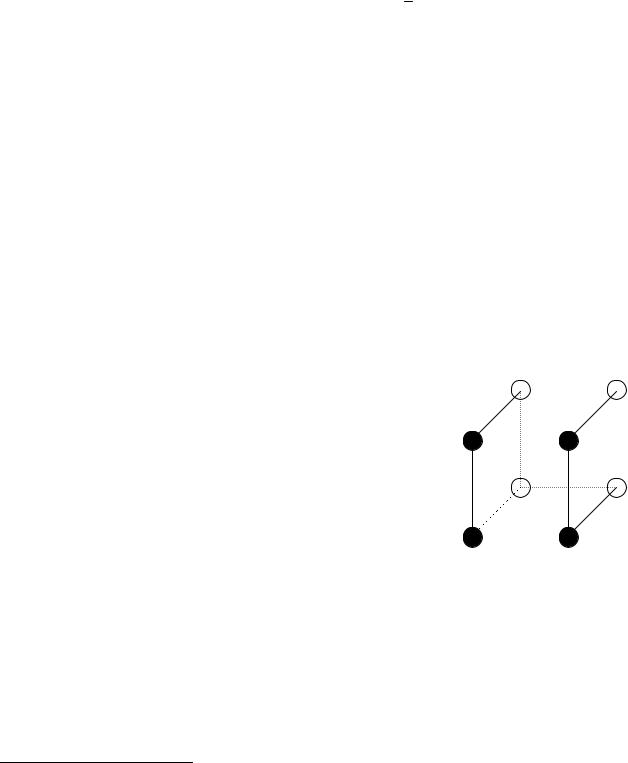
д.н.ф. для булевойАфункции f x , x , x , |
101 |
|
111 |
|
|
||||||||
4 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
||
область истинности которой есть передняя |
|
|
|
|
|
||||||||
грань куба 0,1 3 (рис. 1.4). |
|
|
|
|
|
|
|
|
000 |
|
010 |
|
|
|
|
|
|
|
|
И |
|||||||
Решение. Передняя грань содержит 4 |
|
|
|
|
|
||||||||
вершины, координаты которыхДзапишем в 100 110 |
|||||||||||||
булевой матрице |
|
|
|
|
|
|
|
Рис. 1.4. Единичный куб |
|||||
|
1 |
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
Х |
|
, |
|
|
|
|
|
|
0 |
1 |
1 |
0 |
|
Х |
|
|
|
|
|
|
|
которая, как показано выше, равна троичному вектору 1ХХ, записанному здесь в виде вектор-столбца. Согласно (1.12) получим формулу
Такое сокращение словосочетания дизъюнктивная нормальная форма считается общепринятым, так же как и к.н.ф. – конъюнктивная нормальная форма, определение которой будет дано позже.
12
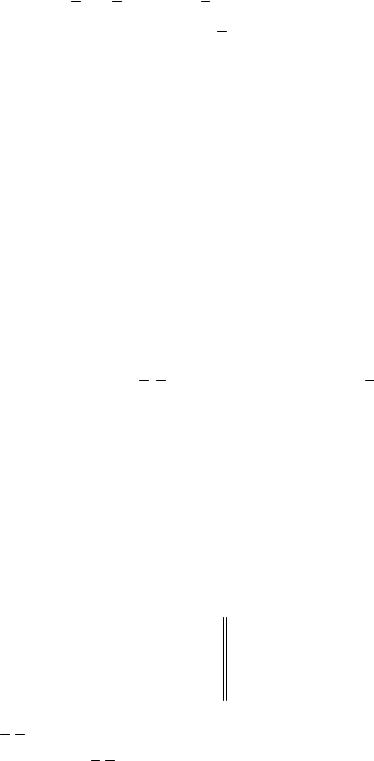
f4 x1, x2, x3 x1 & |
x |
2 & |
x |
3 x1 & |
x |
2 & x3 x1 & x2 |
& x3 |
|
||
|
|
|
x1 & x2 & |
x |
3 , |
|
(1.13) |
|||
|
|
|
|
|
||||||
которая и будет ответом на поставленный вопрос. |
|
|
||||||||
Замечание 1. Для сокращения записи булевых формул допускает- |
||||||||||
Сотсутств скобок, порядок действий определяется согласно их приоритетам. Напр мер, операция умножения имеет больший приоритет и выполняется раньше сложения. Так и конъюнкция (логическое умноже- ) меет больш й приоритет по отношению к дизъюнкции (логиче-
ся опускать символ конъюнкции (подобно тому, как в элементарной алгебре опускается символ операции умножения).
Замечание 2. С помощью круглых скобок в алгебраических формулах задается порядок выполнения арифметических действий, а при
ниеС учетом сделанных замечаний результат решения последнего примера может ыть записан олее компактно, а именно
скому сложен ю). Поэтому в правой части равенства (1.13) круглые скобки можно опуст ть.
стью истинностибкоторойАявляется первый слой куба 0,1 3 (рис. 1.4). Решение. k -м слоем гиперкуба называется множество его вершин,
f4 x1, x2, x3 x1x2x3 x1x2x3 x1x2x3 x1x2x3 .
Будем придерживаться такой, более простой, формы записи буле-
вых формул и дальше.
Пример 2. Найти совершенную д.н.ф. для булевой функции, обла-
сумма координат каждой из которых равна k . Тогда первым слоем куба (рис. 1.4) будет множество вершин {001, 010, 100}. Составим для данной области булеву матрицу
|
|
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
Д |
|||||||||||||||
|
|
0 |
|
1 |
0 . |
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
0 |
0 |
И |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первый столбец данной матрицы задает полную элементарную конъюнкцию – x1x2x3, второй – x1x2x3 и третий – x1x2x3. Тогда искомая д.н.ф. будет f4 x1, x2, x3 x1x2x3 x1x2x3 x1x2x3.
Замечательные свойства стрелки Пирса и штриха Шеффера
Выше доказано, что всего тремя булевыми функциями можно осуществить композицию всех остальных. Однако возможности стрелки Пирса и штриха Шеффера еще более фантастичны. Уникальность этих двух логических операций состоит в том, что каждая из них единолично является «прародительницей» всего мира булевых функций. Иначе го-
13

воря, любая булева функция есть композиция одной изначальной функции – стрелки Пирса (штриха Шафера).
Для доказательства данного утверждения, с учетом уже доказанного тезиса о том, что любая булева функция есть композиция трех логических операций (инверсии, конъюнкции и дизъюнкции), будет достаточным выразить только три эти операции через стрелку Пирса (штрих Шеффера).
Унарную функцию (одноместный предикат) можно получить из бинарной (двуместного предиката) с помощью подстановки вместо од-
ной з переменных (одного из вхождений) постоянной величины либо с |
|||
помощью отождествления двух переменных (слияние двух вхождений в |
|||
одно). Напр мер, |
з бинарной операции стрелка Пирса (штрих Шеффе- |
||
С |
|
x) |
получается логическая функция одной |
|
|||
ра) по формуле x x (или x |
|||
переменной. |
|
|
формулы x x и x x. Пусть |
Теперь |
, как |
||
рассмотримx 0. Тогда на своем входе стрелка Пирса и штрих Шеффера имеют пару 0,0 . Данная вершина принадлежит области истинности данных
Следовательноработают, на выходе получается единица, значение противоположное значению x. Теперь пусть x 1. В этом случае на входе у на-
функц й (см. та л. 1.1, первый элемент строк y9 и y15 соответственно).
ших функций удет пара 1,1 , принадлежащая их области ложности (см. табл. 1.1, четвертый элемент строк y9 и y15 соответственно), т.е. на
выходе будет нуль. Следовательно, формулы |
x x и x |
|
x осуществляют |
||||||||||||||||||||
|
А |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
||||||||||||||||||||||
инверсию (отрицание) величины x. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x x |
x |
и x |
x |
x |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Д |
|
|||||||||||||||
x |
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Рис. 1.5. x x |
x |
|
|
|
|
|
|
|
Рис. 1.6. x |
|
x |
x |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
Эти формулы можно представить в виде логических схем (рис. 1.5 и 1.6). На них операции « » и « » изображены в виде черного ящика с двумя входами и одним выходом. Спаяв два входа в один, мы получили из них устройство, выполняющее функцию инверсии.
14
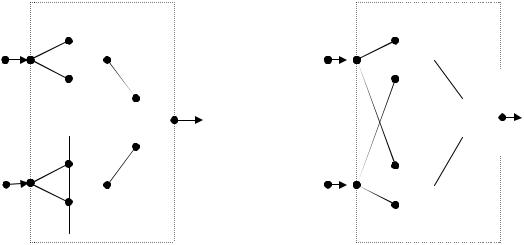
Теперь рассмотрим действие формулы x1 x1 x2 x2 . Ее логическая схема приведена на рис. 1.7.
x1 |
|
|
|
|
& |
|
x1 |
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
|
|
|
y |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сx |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р с. 1.7. x1 |
x1 x2 x2 |
Рис. 1.8. x1 |
x2 x1 |
x2 |
||||||||||||
Пусть |
x1 1 |
|
x2 |
1. |
Тогда |
x1 x1 x2 |
x2 1 1 1 1 |
|||||||||
0 0 1, |
т.е. вершина 1,1 |
лежит в области истинности функции, за- |
||||||||||||||
данной этой формулой. Теперь вычислим, какое значение дает эта фор- |
||||||||||||||||
мула в вершине 0,0 . |
Получим 0 0 0 0 1 1 0. |
В вершине |
||||||||||||||
0,1 получается |
0 0 |
|
Д |
|||||||||||||
1 1 1 0 0 и, наконец, |
в вершине 1,0 |
|||||||||||||||
данная формулабАдаст 1 1 0 0 0 1 0. Полученные результаты |
||||||||||||||||
говорят о том, что данная формула работает как и логическое умноже- |
||||||||||||||||
ние (см. табл. 1.1), т.е. она реализует функцию конъюнкции, и, следова- |
||||||||||||||||
тельно, |
|
|
|
|
|
|
|
И |
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x1 x2 x1 x1 x2 x2 . |
|
|
|
|
|
|||||
Выполним |
|
|
аналогичные |
вычисления |
по |
|
формуле |
|||||||||
x1 x2 x1 x2 , логическая схема которой представлена на рис. 1.8. |
||||||||||||||||
Вершина |
|
|
0,0 |
дает |
x1 x2 x1 x2 0 0 0 0 |
|||||||||||
1 1 0, вершина 0,1 даст 0 1 0 1 0 0 1, пара 1,0 даст |
||||||||||||||||
1 0 1 0 0 0 1, |
а на паре |
1,1 будет 1 1 1 1 0 0 1. |
||||||||||||||
Следовательно, область истинности данной формулы та же, что и у дизъюнкции (см. табл. 1.2), а значит справедливо следующее равенство
x1 x2 x1 x2 x1 x2 .
15
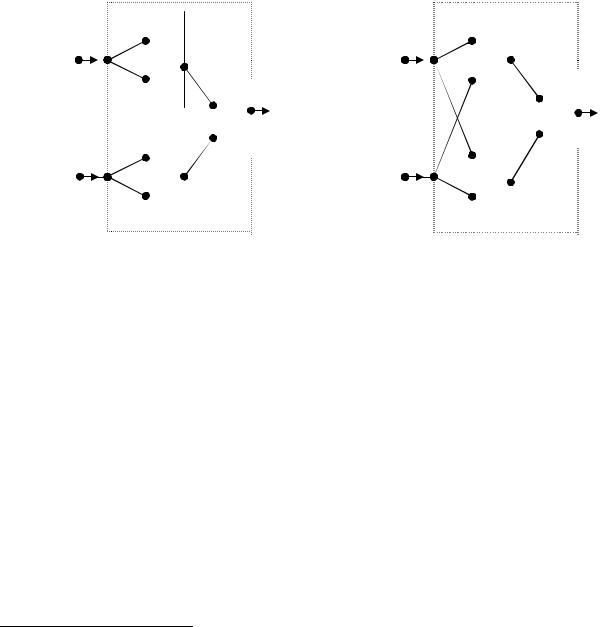
Аналогично |
|
можно |
показать, что |
x1 x2 |
x1 |
|
|
x1 |
|
x2 |
|
x2 и |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
x1 x2 x1 |
|
x2 |
|
|
|
x1 |
|
|
|
x2 . Схемы этих формул приведены на рис. 1.9 и |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
1.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, весь мир булевых функций составлен из «кирпи- |
|||||||||||||||||||||||||||||||||||||||||
чиков» типа « » или |
« |
|
|
|
». |
Каждая из них образует функционально |
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
полную систему (функции подобного рода называют шефферовыми1 |
|||||||||||||||||||||||||||||||||||||||||
[4]). Этот факт используется при создании арифметико-логических уст- |
|||||||||||||||||||||||||||||||||||||||||
ройств м кропроцессоров. |
Используя стандартные электронные схемы |
||||||||||||||||||||||||||||||||||||||||
(элементы), выполняющие функцию « » (или « |
|
»), можно собрать |
|||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
выполнения |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
устройства для |
|
|
|
|
|
|
|
|
|
|
любых арифметико-логических операций. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
бА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 1.9. x1 |
|
x1 |
|
x2 |
|
|
|
x2 |
|
|
|
|
|
|
x1 |
|
|
x2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
Рис. 1.10. |
x1 |
|
|
|
x2 |
|
|
|
|
|||||||||||||||||||||||||||
Однако эти функции плохо сочетаются со спецификой человече- |
|||||||||||||||||||||||||||||||||||||||||
ского мышления. Нам удобнее мыслить, |
используя |
|
более крупные |
||||||||||||||||||||||||||||||||||||||
«кирпичи», контуры которых указаны на рис. 1.5 – 1.10. Поэтому в ма- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||
тематике в качестве базовых (изначальных) булевых функций принимают инверсию, конъюнкцию и дизъюнкцию. Эти операции составляют сигнатуру булевой алгебры.
В цифровой электронике также не ограничиваются только стрелкой Пирса ( микросхема ИЛИ-НЕ) или штрихом Шеффера (микросхема И-НЕ). Электронная промышленность выпускает также микросхемы, реализующие логические операции инверсии, конъюнкции, дизъюнкции, сложения по модулю 2 и эквиваленции.
1 В 1913 г. Г. Шеффер (H.M. Sheffer) показал, что любую логическую операцию можно определить через единственный оператор, названный впоследствии штрихом Шеффера
(прим. автора).
16

Контрольные вопросы и задания
1. Определите совершенные д.н.ф. для двух функций, области истинности которых верхнее переднее и правое переднее ребра куба 0,1 3 (рис. 1.4) соответственно. Затем получите д.н.ф. для функции с областью истинности, равной пересечению указанных выше ребер. Сравните полученные д.н.ф.
2. Чему равна область истинности конъюнкции двух функций – объе-
|
д нен ю |
ли пересечению их областей истинности? |
|
||||||||||||
3. Чему равна область истинности дизъюнкции двух функций – объеди- |
|||||||||||||||
|
нен ю |
пересечению их областей истинности? |
|
||||||||||||
ли |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Что такое функц онально полная система булевых функций? |
|||||||||||||||
С5. уществуют такие улевы функции, которые нельзя выразить че- |
|||||||||||||||
|
рез д зъюнкц ю, конъюнкцию и инверсию? |
|
|||||||||||||
6. |
будет |
x1 |
x2 |
|
x2 и x1 x2 |
|
|||||||||
Докаж те равенства x1 x2 x1 |
|
|
|||||||||||||
7. |
|
|
x1 |
|
|
|
x2 |
|
|
x1 |
|
|
|
x2 . |
|
|
|
|
|
|
|
|
|
|
|||||||
Какую лог ческую операцию |
|
|
выполнять формула |
|
|||||||||||
|
|
|
x1 x1 x1 x1 |
? |
|
||||||||||
|
|
А |
|
||||||||||||
|
|
Практическое занятие №3 |
|
||||||||||||
|
|
ОПТИМИЗ ЦИЯ КЛУ. БУЛЕВА АЛГЕБРА |
|||||||||||||
|
Цель занятия: усвоение методов упрощения дизъюнктивных |
||||||||||||||
нормальных форм с помощью формальных алгебраических преобразо- |
|||||||||||||||
ваний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Краткие сведения о булевой алгебре |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
И |
|||||
|
Данная алгебра, носителем которой является все множество буле- |
||||||||||||||
вых функций, а сигнатурой Д(сигнатура – множество алгебраических |
|||||||||||||||
операций, носитель – множество объектов, на которых эти операции за- |
|||||||||||||||
даны) три логические операции – инверсия, конъюнкция и дизъюнкция, |
|||||||||||||||
– восходят |
к трудам О. Де Моргана и Дж. Буля1. Основные же тожде- |
||||||||||||||
ства этой алгебры непосредственно следуют из табл. 1.1. |
х можно ис- |
||||||||||||||
пользовать при алгебраических преобразованиях сложных булевых формул.
1 Джордж Буль (Boole, 1815 – 1864) – профессор математики в университете г. Корка (Ирландия) – один из основоположников математической логики. Следует отметить, что современная булева алгебра существенно отличается от того, что изложено в его трудах «Математический анализ логики» (1847) и «Исследование законов мысли» (1854). Тем не менее его вклад в современный язык математической логики не может вызывать какихлибо сомнений.
17

Пусть x,y и z произвольные булевы функции. Тогда тождества булевой алгебры будут иметь следующий вид.
войства коммутативности операций и &: |
|
|
|||||||||||||||||||
1а. x y y x, |
1б. x& y y & x. |
|
|
||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
войства ассоциативности операций и &: |
|
|
|||||||||||||||||||
2а. x (y z) (x y) z, |
2б. x&(y & z) (x& y)& z. |
||||||||||||||||||||
войства д стрибутивности операций от & |
и |
& от : |
|||||||||||||||||||
3а. x (y & z) (x y)&(x z), |
|
|
|||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|||||||||||
3б. x&(y z) (x& y) (x& z). |
|
|
|||||||||||||||||||
4а. x |
x |
1 – определение единицы и 4б. x& |
x |
0– |
нуля. |
||||||||||||||||
войства нуля |
единицы: |
|
|
|
|
|
|
|
|
|
|
||||||||||
5а. x 1 1, |
5 . x&1 x, |
6а. x 0 x, |
6б. x&0 0, |
||||||||||||||||||
7а. |
|
|
1, |
7 . |
|
0. |
|
|
|
|
|
|
|
|
|
|
|||||
0 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
Свойства демпотентности операций и &: |
|
|
|||||||||||||||||||
8а. x x x, |
|
|
|
8б. x& x x. |
|
|
|||||||||||||||
Законы поглощения: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
9а. x (x & y) x, |
9б. x&(x y) x. |
|
|||||||||||||||||||
Законы Де Моргана: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
10а. |
|
|
x |
& y, |
10б. x& y |
x |
|
y |
. |
|
|||||||||||
x y |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
||||||||||
Алгебраические преобразования булевых функций |
|||||||||||||||||||||
РассмотримбАнесколько примеров на алгебраические преобразова- |
|||||||||||||||||||||
ния булевых формул. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 1. Упростить выражение (x1 & |
x |
2 ) ( |
x1 & x2 ) (x1 & x2 ). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||
Решение. Используя тождества 1б, 2а и 3б, получим |
|
||||||||||||||||||||
((x1 & x2 ) (x1 & x2 )) (x1 & x2 ) (x1 & x2 x2 ) (x1 & x2 ).
Откуда на основании 1а, 4а, 5б, 3а, 4а, 1б и 5б имеем
(x1 & x2 x2 )& (x1 & x2) (x1 &1) (x1 & x2) x1 (x1 & x2)
x1 x1 & (x1 x2) 1&(x1 x2) (x1 x2)&1 x1 x2 .
Таким образом, (x1 & x2 ) (x1 & x2 ) (x1 & x2 ) x1 x2 . Теперь сравним полученный результат с равенством (1.6). Следовательно, мы нашли те преобразования, о существовании которых говорилось выше.
Пример 2. Упростить совершенную д.н.ф. для импликации. Решение. Согласно (1.9) импликация может быть определена по
формуле x1 x2 (x1 x2 ) (x1 x2 ) (x1 x2 ).
18

Упростим правую часть равенства. Применяя тождества 3б, 1а, 4а, 1б, 5б, 3а, 1а, 4а, 1б и 5б, получим
(x1 x2 ) (x1 x2 ) (x1 x2) (x1 (x2 x2 )) (x1 x2)( x1 (x2 x2 )) (x1 x2) (x1 1) (x1 x2)
x1 (x1 x2) (x1 x1) (x1 x2 ) (x1 x1) (x1 x2 )
С |
|
|
|
|
||
1 ( |
x1 x2) ( |
x1 |
x2) 1 |
x1 x2 . |
|
|
Таким образом, искомая формула будет |
|
|||||
|
|
|
x1 x2 |
x1 x2 . |
(1.14) |
|
Левая часть равенства (1.6) и правая часть равенства (1.14) пред- |
||||||
ставляют д зъюнкц ю неполных конъюнкций. Такие формулы называ- |
||||||
Напримерются сокращенными д.н.ф. В примерах 1 и 2 был осуществлен переход от совершенных д.н.ф. к сокращенным. Сокращенные д.н.ф. можно за-
давать также матр цами, только матрицы эти будут уже не булевыми (как в случае совершенных д.н.ф.), а троичными. Ее столбцы – это троичные векторы, каждый из которых в общем случае может определять грань г перку . , троичные матрицы для сокращенных д.н.ф.,
мерности 1, т.е. ре ро с вершинами 10 и 11. Аналогично второй столбец
Х1={01, 11} и столбцы второй матрицы 0Х={00, 01}, Х1={01, 11}.
полученных в пр мерах 1 и 2, |
удут такими: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x x |
|
: |
x1 |
|
|
|
1 |
Х |
|
|
|
, |
x x |
|
: |
x1 |
|
|
|
0 |
Х |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
2 |
|
x |
2 |
|
|
|
Х |
1 |
|
|
|
|
1 |
2 |
|
x |
2 |
|
|
|
Х |
1 |
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь первый стол ец первой матрицы определяет грань 1Х раз- |
|||||||||||||||||||||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Напомним, что число символов Х в троичном векторе определяет
размерность грани. Например, грань 1ХХ куба 0,1 3 имеет размерность
2 и представляет собой множество {100, 101, 110, 111}, что соответствует четырем столбцам булевой матрицы. Поэтому троичные матрицы
Переход от совершенных д.н.ф. к сокращенным называют минимизацией д.н.ф. Существуют различные алгоритмы минимизации д.н.ф. Они нашли применение в проектировании средств цифровой техники.
по сравнению с булевыми более компактно описывают одну и ту же бу- |
||
леву функцию. |
Д |
|
И |
||
|
||
Наряду с совершенными и сокращенными д.н.ф. в булевой алгебре используются также совершенные и сокращенные конъюнктивные нормальные формы (к.н.ф.), которые также могут задаваться в виде матриц.
Пример 3. Найти совершенную д.н.ф. для инверсии функции.
f x1,x2,x3 x1x2x3 x1x2x3 x1x2x3 x1x2,x3 x1x2x3 . (1.15)
Решение. Функция f x1,x2,x3 имеет область истинности, равную области ложности заданной функции f x1,x2,x3 . Область истинности
19

этой функции согласно (1.15) представлена следующими пятью вершинами {001, 010, 100, 101, 110}. Тогда ее область ложности будет содер-
жать все остальные вершины куба 0,1 3 (рис. 1.4), т.е. множество {000, 011, 111} – ее область ложности и область истинности функции
f x1,x2,x3 . Значит булева матрица функции f x1,x2,x3 имеет вид
x1 0 |
0 |
1 |
|
x1,x2,x3 |
|
|
|
|
|
|
x2 0 |
1 |
1, откуда |
|
x1 |
x |
2 |
x |
3 |
x1x2x3 x1x2x3 . |
|
f |
||||||||||
x3 0 |
1 |
1 |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Пр мер 4. Используя законы Де Моргана (10а, 10б), выразить |
|||||||||||||||||||||||||||||||||||||||||||||||
Сфункц ю з предыдущего примера в виде конъюнкции дизъюнкций. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Решен е. |
Поскольку двойная инверсия пустое преобразование, то |
||||||||||||||||||||||||||||||||||||||||||||||
|
f x1,x2,x3 |
|
f |
x1,x2 ,x3 |
x1 |
x |
2 |
x |
3 |
x1x2 x3 x1x2 x3 |
|
x1 |
x |
2 |
x |
3 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
бА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
x1x2x3 x1x2x3 ( |
x1 |
x |
2 |
x |
3) |
x1 |
x |
2x3 |
x1x2x3 (x1 |
|
x |
2 |
|
|
x |
3) |
||||||||||||||||||||||||||||||
( |
x1 |
|
x2x3 |
)( |
x1 |
|
x2x3 |
) (x1 x2 x3 )(x1 |
|
x |
2 |
x |
3 )( |
x1 |
|
x |
2 |
|
x |
3). (1.16) |
||||||||||||||||||||||||||||
Построение совершенных конъюнктивных нормальных форм
Полученная формула (1.16) для функции (1.15) называется совершенной к.н.ф. Ее можно строить по области ложности функции, следуя такому правилу.
Если область ложности состоит из k вершин, то записывается конъюнкция k одинаковых дизъюнкций из всех переменных (полных элементарных дизъюнкций), от которых зависит функция. Затем ставится знак инверсии над теми переменными, которые соответствуют коор-
динатам вершин, равным единице. |
|
|
|
|
|
И |
|||||||||||||||
Для нашего примера областью ложности было множество {000, |
|||||||||||||||||||||
011, 111}. Поэтому |
|
|
Д |
||||||||||||||||||
|
{(0 |
0 |
0),(0 |
|
1 |
|
1), |
(1 |
|
1 |
|
|
1)} |
. |
|||||||
|
(x x |
2 |
x )(x |
x |
2 |
|
x |
)( |
x |
|
x |
2 |
|
x |
) |
||||||
|
1 |
|
3 |
1 |
|
|
3 |
1 |
|
|
3 |
|
|||||||||
Совершенную к.н.ф. не имеет только одна булева функция – константа «истина», т.к. ее область ложности пустое множество.
Конъюнкции из неполных дизъюнкций образуют сокращенную к.н.ф.
Например, формула (x1 x2 x3)(x2 x3) будет уже сокращенной к.н.ф., т.к. одна из ее дизъюнкций неполная (во второй дизъюнкции отсутствует переменная x1).
20

Сокращенные к.н.ф. нашли применение в алгоритмах исчисления предикатов методом резолюций. На основе данного метода разработан транслятор языка программирования ПРОЛОГ.
Таким образом, микросхемы для выполнения любой логической
функции (логические аппараты без памяти) могут быть собраны на базе |
|||||||||||||||||||||||||||||||||||||||
стрелки Пирса (микросхема ИЛИ-НЕ) либо штриха Шеффера (микро- |
|||||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
схема И-НЕ). Для упрощения этих схем используются алгоритмы ми- |
|||||||||||||||||||||||||||||||||||||||
нимизации д.н.ф., основанные на описанных выше преобразованиях. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы и задания |
|||||||||||||||||||||
выражения |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1. |
Для функц |
f x1,x2 |
,x3 x1x2 |
x2 |
x |
3 найти совершенную д.н.ф. |
|||||||||||||||||||||||||||||||||
2. |
Дайте объяснен е тому, что двойная инверсия – пустая операция. |
||||||||||||||||||||||||||||||||||||||
3. |
Определ те совершенные д.н.ф. и к.н.ф. функции, область истинности |
||||||||||||||||||||||||||||||||||||||
|
которой пересечен |
двух граней 1ХХ0 и Х1Х0. |
|||||||||||||||||||||||||||||||||||||
4. |
Упрост ть |
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
( |
x |
y)( |
y |
|
x)( |
x |
|
y |
)(x y); |
|
|
|
|
|
|
|||||||||||||||||||||||
|
( |
x |
y)( |
y |
|
x) ( |
x |
|
y)(x y); |
|
|
|
|
||||||||||||||||||||||||||
|
( |
x |
y)( |
y |
|
x) ( |
x |
y)(x y); |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
yx ( |
x |
|
y |
)(x y)( |
x |
|
y |
)(x y); |
|||||||||||||||||||||||||||
|
|
x |
y |
||||||||||||||||||||||||||||||||||||
|
( |
x |
y)( |
y |
x)( |
x |
|
y |
)(x y). |
|
|
|
|
||||||||||||||||||||||||||
5. |
Доказать тождества: |
|
|
|
|
|
|
|
Д |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
( |
x |
y)( |
y |
x) ( |
x |
|
y |
)(x y); |
||||||||||||||||||||||||||||||
|
|
xyz xyz |
|
бАxyz xyz xyz xyz xyz xyz |
; |
||||||||||||||||||||||||||||||||||
|
( |
x |
y)( |
y |
x) |
xy |
y x |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||
6. |
Какая функция |
имеет |
|
|
следующую совершенную к.н.ф. |
||||||||||||||||||||||||||||||||||
|
x1 x2 x1 |
x |
2 |
x1 x2 |
x1 x2 ? |
||||||||||||||||||||||||||||||||||
7.Определите совершенные к.н.ф. для логических операций эквиваленции и сложения по модулю 2.
8.Определите совершенные к.н.ф. штриха Шеффера и стрелки Пирса.
9.Какие логические функции не имеют совершенной д.н.ф.?
10.Какие логические функции не имеют совершенной к.н.ф.?
11.Определите совершенные д.н.ф. и к.н.ф. логической функцииИ
fx1,x2,x3 x1 x2x3 x3.
12.Определите совершенные д.н.ф. и к.н.ф. функции, область истинности которой объединение двух граней 1Х10 и Х1Х0.
21
