1.3.Примеры решения тестовых задач [3, 7]

q1+

А

- q2

q2 q. Напряжённость и потенциал в точке

а

а

А равны …

Решение

огласно

пр нц пу

суперпозиции

E E1 E2 ,

1 2

(алгебра ческая сумма). Векторы E1

и E2 показаны на рисунке.

и

А

Е1

- q2

Учитывая, что E1 и E2 направлены в одну

Сq1 +

сторону, то

а

Е2

а

…

бА

E E1 E2

2k

q

,

a2

k

q1

k

q1

k

q

k

( q)

0.

a

a

a

a

Ответ: E 2k

q

, 0.

a2

2. Работа сил электрического поля при перемещении заряда –2 мкКл

Д1 2

из точки поля с потенциалом 20 В в точку с потенциалом 40 В равна

Решение

И

Работа сил поля по перемещению заряда q в электрическом поле

вычисляется по формуле

A q( ), где 1 и 2

–

потенциалы

начальной и конечной точек поля. Тогда

A q(

2

) ( 2 10 6) (20 40) 40 10 6

Дж.

1

Ответ: 40 10-6

Дж.

кинетической энергии

qU

m 2

Отсюда скорость частицы будет

.

2

С

p

m

равна

2qU

.

Следовательно,

отношение скоростей протона и

p

m

электрона

m

e

.

e

mp

точки B, C, D и E

рисунок) з точки A в

Ответ:

e .

e

mp

бА

A

4. В электр ческом поле точечного заряда q (см.

перемещают

заряд

q0.

Для

работы

по

B

+q

E

перемещен ю заряда q0 (q0<0) в поле заряда q

справедливо соотношение …

C

D

Решение

q0

в поле заряда q

Работа сил

поля

по

перемещению заряда

Д

вычисляется по формуле A q0( 1

2 ), где 1

и 2

– потенциалы

начальной и конечной точек поля. Учитывая, что потенциал поля

точечного

заряда

q вычисляется по формуле k

q

и все

точки

r

лежат на

окружности, т.

е. r R, получим,

что

1 = 2.

Тогда

AAB AAC AAD AAE 0.

И

пропорциональна расстоянию до нити:

E

; напряжённость

2 0 r

поля равномерно заряженной бесконечной плоскости не зависит от

расстояния до плоскости: E

.

2 0

Ответ: 1) точечный заряд, E k

q

;

2) равномерно заряженная

r2

длинная

н ть, E

;

3)

равномерно заряженная бесконечная

С2 0 r

плоскость,

E

.

2 0

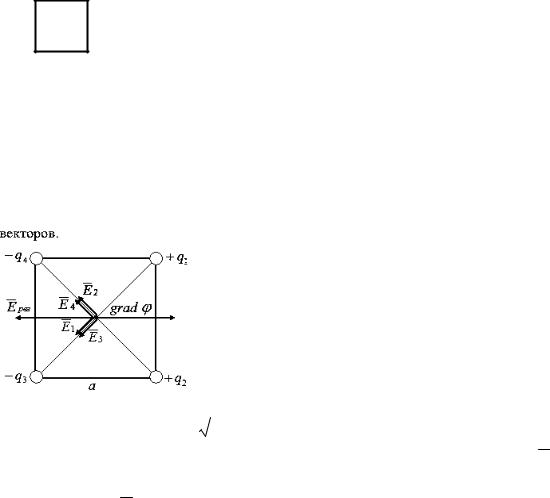
6. Каждый

бА

з четырёх одинаковых по модулю точечных зарядов (см.

- q

+q

р с.),

расположенных

в

вершинах

квадрата,

создаёт в точке пересечения диагоналей

-q

+q

электрическое

поле,

напряжённость

которого

равна E.

Градиент потенциала поля в этой точке

равен ___ и направлен горизонтально …

Решение

Величина напряжённости поля точечного заряда определяется

по формуле E

1

q

,

где

0

– электрическая постоянная, а r –

4 0 r2

расстояние от заряда до точки. Поскольку

все заряды одинаковы по величине и

рассматриваемаяДточка одинаково удалена

от

каждого

заряда, модули

векторов

E1, E2, E3, E4 равны, т. е.

E1 E2

E3 E4,

а

Eрез

образует диагональ квадрата со

стороной 2Е (смИ. рисунок). Модуль

напряженности

результирующего поля в

центре квадрата Eрез.

2

E. Учитывая связь напряженности поля и

2

Работа с л электростатического поля по перемещению заряда q

дляодинаковыйтраектор 2–3,поскольку 2

3 , аq< 0. А> 0 для траектории 4–1.

из точки 1 в точку 2

определяется

по формуле: A12 q( 1 2).

СОтсюда следует, что

А12=0,

если

1 2. Точки, имеющие

потенц ал лежат на одинаковом расстоянии от заряда,

бА

Q

создающего поле k

, поэтому А = 0 для траектории 1–2. А < 0

r

Ответ: 1) А = 0, траектория 1–2; 2)

< 0, траектория 2–3;

3) А > 0, траектория 4–1.

8. Жёсткий электрический диполь находится в однородном

электростатическом

поле. Момент

сил,

E

действующий на диполь, направлен …

Решение

И

Во

внешнем

электрическом поле на электрический диполь

действует

момент

сил M p ДE( p – электрический дипольный

1

5 2y2.

Вектор

напряжённости

A

2

электрического поля в точка А будет иметь

4

3

направление, показанное стрелкой …

0

Решение

Напряжённость поля E grad .

Тогда E

d

4y. Таким

образом вектор E направлен вниз, в направлении 3.

dt

С

Ответ: 3.

вакууме точечного заряда q на расстоянии r от него пропорциональна

и

…

Решение

бА1

определяется по формуле

0E2, где Е – величина напряжён-

2

ности

электрического поля точечного

заряда. В нашем случае

E

q

и, следовательно,

q2

~ r 4.

4

r

2

4

2

0

Д32 r

0

Ответ: ~ r 4.

11. Для электронной поляризации диэлектриков характерно …

Решение

И

возникновен

у молекул индуцированного дипольного момента за

счёт

деформац

электронных орбит под влиянием внешнего

электр ческого поля. Тепловое движение неполярных молекул никак

С

не

на возн кновение у них индуцированных электрических

моментов, которые всегда совпадают по направлению с вектором

напряжённости электр ческого поля (это связано с очень малой

инертностью электронов).

влияет

бесконечно

Ответ: возн кновение у молекул индуцированного дипольного

момента при помещен диэлектрика во внешнее электрическое поле.

12. Если

А

длинный цилиндр радиуса R равномерно заряжен

с объёмной плотностью заряда , то его линейная плотность заряда

равна ...

Д

Решение

Объёмная плотность заряда цилиндра определяется по формуле

q

,

где q – заряд цилиндра, V – его объём. Если учесть, что объём

V

И

цилиндра V R2l,

где l – длина цилиндра, то линейная плотность

заряда

q

выражается через объёмную плотность заряда

l

q

q

следующим образом: R2 .

R2

V

R2l