
2065
.pdf
YРОЛЗ
YРОЗ
gРОЗ 

 L3|2
L3|2 








YРОПЗ
Задатчик
YРОЛ
KД
hШтЛ
Л |
e |
-tгp |
1 |
КШ |
|
|
Трр+1 |
р |
|
П |
e-tгp |
1 |
КШ |
|
|
|
Трр+1 |
р |
|
KД |
Y |
|
hШтП |
|
|
|
|
||
|
|
|
|
|
|
РОЛ |
|
|
|
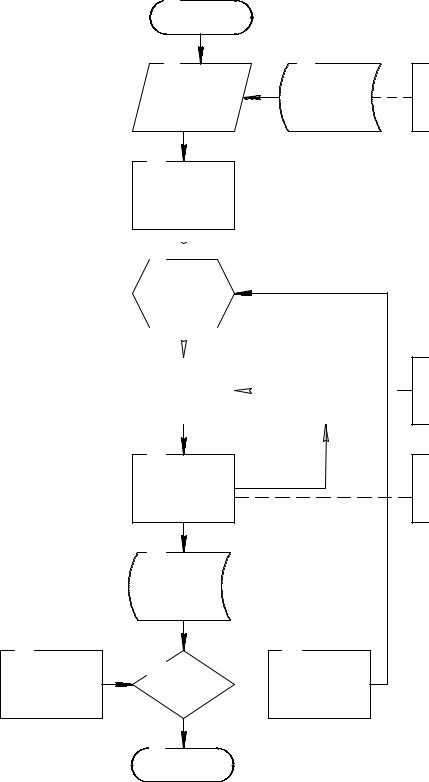
Рис. 2.8. Структурная схема математической модели системы управления рабочим органом автогрейдера
50
H1
Время моделирования
A2
Начало
B2
Ввод исходных данных
B3
Значения параметров
YРОЗ, РОЗ ,L3, г ,
ТР,KШ,с,+iзол,-iзол
C2 |
Расчет
YРОПЗ,YРОЛЗ
D2 
Цикл для t=0 с шагом t
|
|
E2 |
|
|
|
|
|
|
|
|
E3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Расчет |
|
|
Мат.модель |
|
|
|||||||||||
hШтП,hШтЛ,, П, Л |
|
|
|
|
автогрейдера |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2
Расчет
YРО,YРОП,YРОЛ, РО
G2
Запись файла данных
H3
H2Конец Нет
пути? 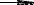 t=t+ t
t=t+ t
Да
I2
Конец
Колея машины,проектные геометрические параметры, параметрыЭГП
Отклонения фактических координатотзаданных, ход штоков
Координатырежущей кромки отвала
Рис 2.9. Блок – схема алгоритма реализации математической модели системы управления рабочим органом автогрейдера
51
2.4. Математическая модель процесса копания грунтов
На точность планировочных работ существенное влияние оказывают микрорельеф обрабатываемой поверхности и реакция разрабатываемого грунта, действующая на РО. Ее необходимо учитывать при составлении математической модели автогрейдера. Для учета силы реакции грунта на РО на рис. 2.10 представлен фрагмент основной расчетной схемы.
Элементы ходового оборудования представлены моделями, содержащими упруго-вязкие элементы (модели Фохта) [102,110].
На схемах введены следующие обозначения: Fx, Fy, Fz - горизонтальная, вертикальная и поперечная составляющие вектора равнодействующей реакции грунта на РО; R1, R2, ..., R6 - силы реакций грунта на элементы ходового оборудования; С1, С2, ..., С6 - коэффициенты жесткости элементов ходового оборудования; b1, b2, ..., b6 - коэффициенты вязкости элементов ходового оборудования.
В дополнение к допущениям, изложенным при составлении математической модели автогрейдера, введены следующие допущения:
наложенные на автогрейдер связи являются голономными
истационарными;
в шарнирных соединениях отсутствуют силы сухого
трения;
элементы ходового оборудования имеют одинаковые упруго-вязкие свойства;
упруго-вязкие свойства гидрооборудования не учитываются;
внешние силы, действующие на автогрейдер рассматриваются как сосредоточенные;
реакция грунта приложена к центру режущей кромки РО;
призма волочения набрана; рассматриваются только вертикальные перемещения РО.
С учетом указанных допущений можно записать:
YF = YРО + YR |
(2.44) |
где YF - вертикальная координата грунта под центром отвала; YРО - вертикальная координата грунта под центром отвала без учета действия сил реакции грунта; YR - изменение вертикальной координаты центра отвала под действием реакции грунта.
52





 b2 C2
b2 C2 



 R2
R2
Z |
|
C6 |
b6 |
V |
|
4 |
R6 |
b |
|
C4 |
|
R4 |
|
Fz 


Fx
Fy




 b1
b1
C1 




 R1
R1
 X
X
Y
C5 |
b5 |
O |
|
3 |
R5 |
b |
|
C3 |
|
R3 |
|
Рис. 2.10. Фрагмент расчетной схемы для определения влияния реакции грунта на позиционирование рабочего органа
53
Используя уравнения для определения YРО можно определитьYR, зная Y1R и YБR - изменение условных вертикальных координат средних точек переднего моста и балансирной тележки автогрейдера под действием силы сопротивления копанию.
Из принятой расчетной схемы можно записать [102]:
|
|
Rпр |
|
|
|
Y |
|
i |
, |
(2.45) |
|
Ciпр |
|||||
iR |
|
|
|
где YR - изменение вертикальной координаты центральной точки режущей кромки отвала автогрейдера; Rпр и Cпр - соответственно приведенные к центральной точке режущей кромки отвала значения вертикальных компонентов изменения вектора силы и жесткости ходового оборудования.
На рис. 2.11 представлена структурная схема, описывающая математическую модель влияния реакции грунта при копании на точность позиционирования РО, а на рис. 2.12 - блок-схема алгоритма реализации этой модели.
Используя принятые допущения, и выводы, сделанные при анализе теорий копания, можно компоненты вектора реакции грунта на РО при выполнении планировочных работ представить случайной функцией состоящей из двух составляющих [102]: тренда Fт , зависящего от толщины срезаемой стружки h, физико-механических свойств грунта, параметров РО и флюктуаций Fф . Численные
значения Fт можно определить по теории К.А.Артемьева, а
численные значения Fф - исходя из корреляционной функции флюктуации.
2.5. Математическая модель микрорельефа обрабатываемой поверхности
Анализ рабочего процесса автогрейдера при планировочных работах показал, что одним из возмущений, действующих на РО через ходовое оборудование и раму машины и в итоге, влияющих на
точность |
обработки |
поверхности, |
является |
микрорельеф |
обрабатываемого |
|
|
грунта. |
|
54

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение FYЛ |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение FФY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
YF |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
FФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Определение YR |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FX |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
YРО |
|
|
|
|
|
|
|
|||||
Определение FФX |
|
|
|
|
|
|
sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение FПР |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение FXЛ |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.11. Структурная схема математической модели копания
55

J1
Время моделирования
A2
Начало
B2


Ввод исходных данных
C2 |
РасчетFУЛ
D2 
РасчетFy
E2
Цикл для t=0 с шагом t
F2
РасчетFФ
G2
РасчетFРО
H2
Расчет YiR
I2
B3
Значения параметров
0 , , 1,B,пр, р,h
D3
Значение параметра
F3
Значения параметров
Ф , Ф , Ф
Запись файла данных
J3
J2Конец Нет
пути?  t=t+ t
t=t+ t
Да
K2
Конец
Свойства грунта и параметрыотвала
Вертикальная составляющая силысопротивления резанию грунта при лобовомкопании
Вертикальная составляющая силысопротивления резанию грунта при косомкопании
Высокочастотная составляющая реакции грунта
Реакция грунта на отвале автогрейдера
Изменение вертикальной координатыi-ой точки автогрейдера
Рис. 2.12. Блок-схема алгоритма реализации модели влияния реакции грунта
56
Таким образом, составление математической модели микрорельефа является важным этапом в разработке обобщенной математической модели автогрейдера, осуществляющего планирование. Это позволит установить основные закономерности движения автогрейдера по опорной поверхности, выявить характер влияния на точность обработки грунта параметров обрабатываемого микрорельефа.
В работе использовались для моделирования микрорельефа корреляционные функции разных типов, определяемые выражениями
(1.18) и (1.19).
Для реализации случайного микрорельефа на ЭВМ используется алгоритм, основанный на преобразовании стационарной последовательности x(n) независимых нормально распределенных случайных чисел (дискретный белый шум) с параметрами: mx = 0 и σx =1 в последовательность y(n), для чего используется рекуррентное уравнение.
Рекуррентное уравнение, определяемое видом корреляционной функции, описывает поведение некоторого дискретного фильтра, который преобразует подаваемый на его вход белый дискретный шум, в случайный процесс с заданной корреляционной характеристикой. Передаточная функция этого фильтра в общем виде имеет вид:
|
|
|
|
|
|
|
l |
|
|
|
a0 |
a1z ... al z |
l |
|
ak zk |
|
|
||
y(z) |
|
|
k 0 |
. |
(2.46) |
||||
|
|
|
m |
||||||
|
1 q1z |
... qm z |
m |
|
|
|
|||
|
|
|
|
1 qk zk |
|
|
|||
k 1
Зная передаточную функцию (2.46) можно сформировать структурную схему дискретного фильтра (рис. 2.13), описываемого рекуррентным уравнением.
Cглаживание микрорельефа шинами за счет пятна контакта моделируется в соответствии с (1.35).
На рис. 2.14 приведены профили микрорельефа, полученные в программном комплексе Matlab-Simulink [106].
На рис. 2.15 представлена структурная схема математической модели микрорельефа обрабатываемой поверхности. На рис. 2.16 представлена блок-схема алгоритма реализации математической модели микрорельефа обрабатываемой поверхности.
57

x(n)
z |
|
z |
z |
z |
a0 |
a1 |
a2 |
al-1 |
al |
z |
z |
z |
z |
q1 |
q2 |
qm-1 |
qm |
y(n)
Рис. 2.13. Структурная схема дискретного фильтра
Y, м |
Несглаж |
|
Сгла |
X0, м
Рис. 2.14. Профили микрорельефа: 1 - по правой колее, 2 - по левой колее
На основе математической модели можно смоделировать микрорельеф грунта с заданными характеристиками [27].
58

x(n),
mx=0, x=1
Дискретный фильтр
a0 |
a1 |
|
|
|
|
z |
|
|
|
|
|
q1 |
q2 |
yП(n) |
Сглаживание шинами |
Y1П |
|
|
X+X0 |
||||
|
|
1 |
|
||
z |
z |
|
y(X)dX |
|
|
|
2X0 |
|
|||
|
|
yЛ(n) |
|
X-X0 |
1Л |
|
|
|
|
||
a0 |
|
|
|
|
Y |
|
|
|
|
|
|
z |
q1 |
Рис. 2.15. Структурная схема математической модели микрорельефа
59
