

е р и я в н у т р и в у з о в с к и х СибАДИм е т о д и ч е с к и х у к а з а н и й С и б А Д И
Министерство науки высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
« ибирский государственный автомо ильно-дорожный университет (СибАДИ)» Кафедра «Автомат зация производственных процессов и электротехника»
И.В. Лазута
МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА СИНТЕЗА СИСТЕМ УПР ВЛЕНИЯ
Методические указания к лабораторным работам
Омск ▪ 2018

УДК 681.5 БКК 32.965
Л17
_____________________________
Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, причиняющей вред их здоровью и развитию» данная продукция маркировке не подлежит.
_____________________________
Рецензенты:
канд. техн. наук, доц. С.Д. Игнатов (СибАДИ)
Работа утверждена редакционно-издательским советом СибАДИ в качестве СибАДИметодических указаний.
Лазута,ИванВас льевич.
Л17 Математ ческие методы анализа и синтеза систем управления [Электрон-
ный ресурс] : метод ческие указания к лабораторным работам /И.В. Лазута. –
Электрон. дан. – Омск : С АДИ, 2018. – URL: http://bek.sibadi.org/cgi-bin/
irbis64r plus/cgiirbis 64 ft.exe. - Режим доступа: для авторизованных пользователей.
Содержат кратк е теоретические сведения, методику и порядок выполнения лабораторных работ по теоретическому исследованию, математическим методам анализа и синтеза л нейных нелинейных систем автоматического управления.
Имеют нтеракт вное оглавление в виде закладок. Содержат ссылки на видеоматериалы обучающего и демонстрационного характера, которые воспроизводятся с помощью проигрывателя Windows Media.
Предназначены для выполнения ла ораторных работ по дисциплине «Математические методы анализа и синтеза систем управления» обучающимися всех форм по направлениям магистратуры «Автоматизация технологических процессов и производств» и «Управление в технических системах».
Подготовлены на кафедре « втоматизация производственных процессов электротехника».
Мультимедийное издание (1,8 МБ)
Системные требования : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ; DVD-ROM ;
1 ГБ свободного места на жестком диске ; программа для чтения pdf-файлов Adobe
Acrobat Reader ; Foxit Reader
Техническая подготовка Н.В. Кенжалинова Издание первое. Дата подписания к использованию 17.08.2018
Редакционно-издательский комплекс СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПК СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1
ФГБОУ ВО «СибАДИ», 2018
|
ОГЛАВЛЕНИЕ |
Введение ........................................................................................................................ |
3 |
Лабораторная работа № 1............................................................................................. |
4 |
Лабораторная работа № 2........................................................................................... |
10 |
Лабораторная работа № 3........................................................................................... |
15 |
Лабораторная работа № 4........................................................................................... |
19 |
СибАДИ |
|
Лабораторная работа № 5........................................................................................... |
24 |
Лабораторная работа № 6........................................................................................... |
30 |
Лабораторная работа № 7........................................................................................... |
42 |
Лабораторная работа № 8........................................................................................... |
51 |
Лабораторная работа № 9........................................................................................... |
60 |
Лабораторная работа № 10......................................................................................... |
67 |
Лабораторная работа № 11......................................................................................... |
74 |
Лабораторная работа № 12......................................................................................... |
80 |
Лабораторная работа № 13......................................................................................... |
86 |
Лабораторная работа № 14......................................................................................... |
98 |
Лабораторная работа № 15....................................................................................... |
104 |
Приложен я............................................................................................................... |
111 |
Библиограф ческ й сп сок ..................................................................................... |
122 |
|
ВВЕДЕНИЕ |
Целью проведения данных лабораторных работ является |
|
получение навыков математического моделирования, теоретического |
|
исследования, использования математических методов анализа и |
|
синтеза линейных нелинейных автоматических систем управления. |
|
3
Лабораторная работа № 1
Структурный анализ линейных систем управления
Цель работы − изучить структурный анализ линейных автома-
тических систем управления методом графов. |
|
|
|
|||||||
СибАДИ |
||||||||||
|
|
|
Общие сведения |
|
|
|
|
|||
|
Графом модели с стемы управления является структурная схема, |
|||||||||
состоящая |
з дуг |
вершин. Дуга соответствует звену и на схеме изо- |
||||||||
бражается отрезком л н и со стрелкой, указывающей направление рас- |
||||||||||
пространен я с гнала. Дуга начинается и кончается в вершине [3, 4]. |
||||||||||
|
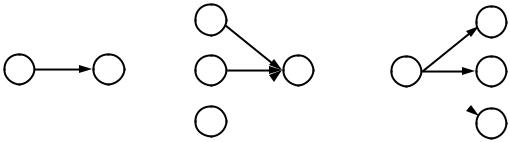
Верш на на графе изо ражается кружком и определяет перемен- |
|||||||||
ную. Если к верш не подходит одна дуга, |
то она только она опреде- |
|||||||||
ляет выходную вел ч ну дуги (рис. 1.1, а), если же в вершину входят |
||||||||||
несколько дуг, то она соответствует сумме выходных переменных |
||||||||||
этих дуг (р |
с. 1.1, |
). |
|
|
|
|
|
|
|
|
|
Начальная вершина |
дуги |
определяет |
её входную переменную |
||||||
(рис. 1.1, в). Вершина графа, имеющая только выходящие из нее д уги, |
||||||||||
определяет внешнее воздействие и называется входной вершиной графа. |
||||||||||
|
|
|
x1 |
W1 |
|
W1 |
y1 |
y1 = W1g |
||
|
W |
|
|
|
|
|
|
|||
x |
y |
x2 |
|
W2 |
y |
g |
W2 y2 y2 = W2g |
|||
|
|
|||||||||
|
|
y = Wx |
|
|
|
y = ∑Wixi |
|
Wn |
|
|
|
|
|
xn |
|
Wn |
|
yn |
yn = Wng |
||
|
|
|
|
|
|
|
|
|||
|
а |
|
|
|
|
|
|
в |
|
|
Рис. 1.1. Представление структуры системы в виде графов:
а – выходная величина; – сумма выходных переменных; в – входная вершина
Последовательность дуг W1, W2, ..., Wn (не обязательно разных), для которых конечная вершина xi, дуги Wi является начальной вершиной дуги Wi+1 (i = 1, 2, ..., n – 1), называется ориентированным маршрутом или ормаршрутом. Ормаршрут называется замкнутым,
если конечная вершина дуги Wn совпадает с начальной вершиной дуги W1, и незамкнутым в противном случае.
4
|
Ормаршрут, в котором все дуги разные, называется путем от |
||||||||||||||||
начальной вершины х0 к конечной вершине хп, если он не замкнут, и |
|||||||||||||||||
контуром, если он замкнут (х0 и хп |
совпадают). Путь и контур на- |
||||||||||||||||
зывают простыми, если все вершины х0, х1, ..., xn различны. Простой |
|||||||||||||||||
путь также называют прямым путем [3, 4]. |
|
|
|
|
|
|
|||||||||||
|
Два контура называются несоприкасающимися, если они не |
||||||||||||||||
имеют общих вершин. Три, четыре |
|
т.д. контура называются несо- |
|||||||||||||||
прикасающимися, если любая пара из этих контуров является несо- |
|||||||||||||||||
прикасающейся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
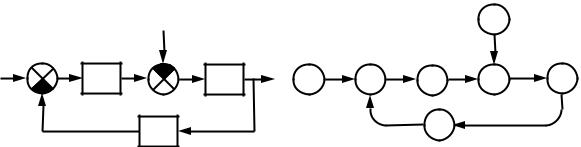
Граф модели с стемы управления можно построить по струк- |
||||||||||||||||
турной схеме её модели (рис. 1.2), выполнив следующие действия: |
|||||||||||||||||
|
1) сумматоры заменить вершинами с соответствующими вы- |
||||||||||||||||
ходными переменными; |
|
|
|
|
|
|
|
|
|
||||||||
|
2) |
звенья с передаточными функциями W заменить дугами W; |
|||||||||||||||
если выходная переменная подается в отрицательный вход суммато- |
|||||||||||||||||
ра, то указанное звено заменить дугой –W; |
|
|
|
|
|
|
|||||||||||
|
3) |
каждой переменной, в том числе переменной, |
соответствую- |
||||||||||||||
щей внешнему воздействию, сопоставить свою вершину. |
|
||||||||||||||||
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
g |
|
ε |
|
x |
1 |
x |
2 |
y |
|
1 |
|
W |
|
1 |
W2 |
|
|
|
|
|
W1 |
|
|
|
W2 |
g |
ε |
1 |
x1 |
x2 |
y |
||||
+ |
–x3 |
+ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
–1 |
|
|
W3 |
|
|||||
|
|
|
|
W3 |
|
|
|
|
|
|
x3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.2. Преобразование структурной схемы модели системы в граф |
|
|||||||||||||||
|
Определителем графа (подграфа) называется передаточная |
||||||||||||||||
функция , характеризующая совокупность всех замкнутых цепей |
|||||||||||||||||
системы, содержащих обратные связи [4]: |
|
|
|
|
|
|
|||||||||||
|
|
|
∆ =1 − ∑W0 j |
+ ∑W0 jW0k |
− ∑ W0 jW0kW0l |
+.... |
(1.1) |
||||||||||
|
|
|
|
|
|
j |
|
|
j,k |
|
j,k,l |
|
|
|
|
|
|
СибАДИ |
|||||||||||||||||
|
Здесь в первой сумме W0j – передаточная функция j-го простого |
||||||||||||||||
контура, равная произведению передаточных функций дуг, входящих |
|||||||||||||||||
в этот контур, и суммирование производится по всем простым конту- |
|||||||||||||||||
рам графа; во второй сумме W0jW0k |
– произведение передаточных |
||||||||||||||||
функций j-гo и k-го простых контуров, не к асающихся ни дугами, ни |
|||||||||||||||||
вершинами, суммирование осуществляется по всем парам не касаю- |
|||||||||||||||||
щихся контуров; |
в третьей сумме W0jW0kW0l – произведение переда- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
точных функций j-го, k-го и l-го простых контуров, не касающихся ни |
||||||||||||||||||||
дугами, ни вершинами, суммирование производится по всем тройкам |
||||||||||||||||||||
не касающихся контуров; и т. д. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Подграфом i-го прямого пути называется подграф, который по- |
|||||||||||||||||||
лучается из исходного графа отбрасыванием всех дуг и вершин i-го |
||||||||||||||||||||
пути, а также всех дуг, начинающихся или кончающихся на вершинах |
||||||||||||||||||||
этого пути. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Правило несоприкасающихся контуров (теорема Мейсона). |
|||||||||||||||||||
|
Передаточная функция системы управления относительно входа |
|||||||||||||||||||
g и выхода y определяется следующим образом [3, 4]: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
W |
|
|
= |
1 n |
|
∆ |
|
|
. |
|
|
|
|
(1.2) |
|
|
|
|
|
|
|
|
∑W |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
yg |
|
∆ i=1 пi |
|
i |
|
|
|
|
|
|
|
||
где |
– определ тель графа системы управления; Wni – передаточная |
|||||||||||||||||||
функц я i-го прямого пути от начальной вершины g |
к конечной вер- |
|||||||||||||||||||
шине y; т – общее ч сло таких прямых путей; |
i – определитель под- |
|||||||||||||||||||
графа i-го прямого пути. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
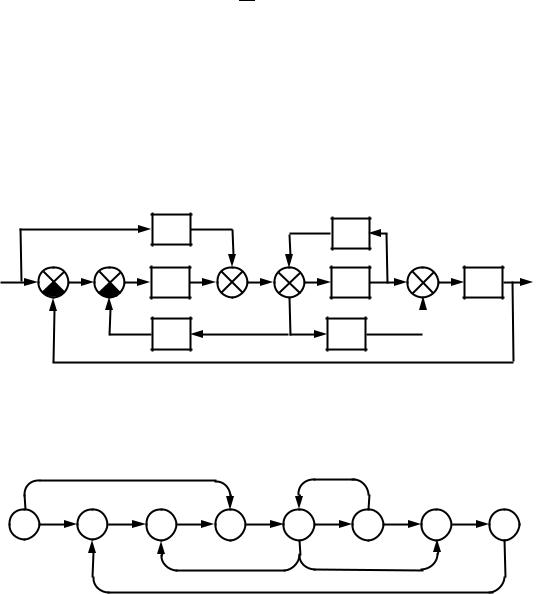
Пр мер. Постро ть граф системы управления по структурной |
|||||||||||||||||||
схеме модели системы (рис. 1.3) по теореме Мейсона определить пе- |
||||||||||||||||||||
редаточную функцию системы Wyg относительно входа g и выхода y. |
||||||||||||||||||||
|
|
|
|
|
W0 |
|
|
|
|
|
|
|
|
|
W5 |
|
|
|
|
|
|
g |
|
ε |
x1 |
W1 |
|
|
|
+ |
x2 + |
|
x3 |
W3 |
|
+ |
x5 |
W6 |
y |
||
|
+ |
–y |
+ |
– |
|
|
+ |
+ |
x3 |
|
|
|
x4 |
+ |
|
|||||
|
|
|
W2 |
|
|
|
|
|
|
|
W4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 1.3. Структурная схема модели системы управления |
|
|||||||||||||||||
|
Граф системы управления представлен на рис. 1.4. |
|
|
|||||||||||||||||
|
|
|
|
W0 |
|
|
|
|
|
|
|
|
|
|
W5 |
|
|
|
|
|
СибАДИ |
||||||||||||||||||||
|
g |
1 |
ε |
1 |
x1 |
W1 |
|
x2 |
1 |
x3 |
|
W3 |
x4 |
1 |
x5 |
W6 |
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
–1 |
|
|
|
–W2 |
|
|
|
|
|
W4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.4. Граф модели системы управления |
|
|
|
|||||||||||||
6

От вершины g до вершины y имеются четыре прямых пути. Передаточные функции этих путей равны:
С |
|
|
Wп1 =W0W3W6 ; |
|
|
|
|
|
(1.3) |
||||||||
|
|
Wп2 =W0W4W6 ; |
|
|
|
|
|
(1.4) |
|||||||||
|
|
Wп3 |
=W1W3W6 ; |
|
|
|
|
|
|
(1.5) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Wп4 =W1W4W6 . |
|
|
|
|
|
(1.6) |
|||||
Подграф 1-го пути состоит из вершин e и d, 2-го пути — из вер- |
|||||||||||||||||
делит |
|
|
|
|
|
|
|
|
|
|
|
||||||
шин , d |
z; подграф 3-го пути есть пустой граф, подграф 4-го пути |
||||||||||||||||
состоит |
з верш ны z. И так как все они не имеют контуров, их опр е- |
||||||||||||||||
|
равны ед н це: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∆1 = ∆2 |
= ∆3 |
= ∆4 =1. |
|
|
|
(1.7) |
|||||
|
б |
|
|
|
|
|
|
|
|||||||||
Граф с стемы управления имеет четыре простых контура. Их |
|||||||||||||||||
передаточные функц |
|
меют вид |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
W01 |
= −W1W2 ; |
|
|
|
|
|
|
(1.8) |
|||
|
|
|
|
|
А |
|
|
||||||||||
|
|
|
|
|
|
W02 =W3W5 ; |
|
|
|
|
|
|
(1.9) |
||||
|
|
|
|
|
|
W03 = −W1W3W6 ; |
|
|
|
|
|
(1.10) |
|||||
|
|
|
|
|
|
W04 = −W1W4W6 . |
|
|
|
|
|
(1.11) |
|||||
|
|
|
|
|
|
|
|
Д |
|
||||||||
Несоприкасающихся пар контуров нет. Поэтому определитель |
|||||||||||||||||
графа имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∆ =1−∑W0 j =1−(W01 +W02 +W03 +W04 ) . |
(1.12) |
|||||||||||||||
|
|
|
|
|
j |
|
|
|
|
|
|
|
И |
||||
Для искомой передаточной функции системы Wyg относительно |
|||||||||||||||||
входа g и выхода y по теореме Мейсона получаем |
|
|
|
|
|||||||||||||
|
W |
yg |
= |
1 |
(W ∆ +W |
∆ |
2 |
+W |
∆ |
3 |
+W |
∆ |
4 |
)= |
|
||
|
|
|
|||||||||||||||
|
|
|
∆ |
п1 1 |
п2 |
|
п3 |
|
п4 |
|
. |
(1.13) |
|||||
|
|
W0W3W6 +W0W4W6 +W1W3W6 +W1W4W6 |
|||||||||||||||
|
|
|
|
||||||||||||||
1+W1W2 −W3W5 +W1W3W6 +W1W4W6
Применение теоремы Мейсона особенно удобно для структурных схем моделей систем управления с перекрёстными связями, т.е. с пресекающимися контурами, так как при этом заметно упрощается вычисление определителя графа системы за счёт отсутствии сумм произведений передаточных функций несоприкасающихся контуров.
7
|
|
Исходные данные для выполнения работы |
|
|
|
|
|||||||||||||||||||
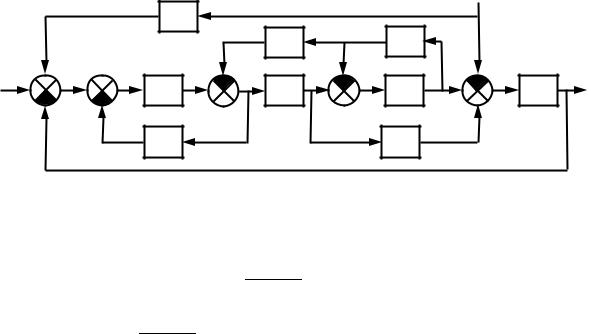
На рис. 1.5 представлена структурная схема модели линейной |
|||||||||||||||||||||||||
системы автоматического управления с входным g, выходным y и |
|||||||||||||||||||||||||
возмущающим f воздействиями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
W9 |
|
|
|
|
|
|
x7 |
|
|
|
|
f |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
W7 |
|
|
|
|
W6 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g |
+ ε |
|
x1 |
|
W1 |
|
|
– x2 |
W3 |
|
x3 |
|
|
– x4 |
W4 |
+ |
|
– x6 |
W8 |
y |
|
||||
+ |
– |
+ |
– |
|
|
|
|
+ |
|
|
+ |
|
|
|
|
x5 |
|
|
|
|
|
||||
Сy |
W2 |
|
|
|
|
|
|
|
|
|
|
|
W5 |
|
|
+ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р с. 1.5. Структурная схема модели линейной системы управления |
|
|
|
||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Передаточные функции системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
W |
= K1 |
; |
W = K |
|
; |
W = |
|
K3 |
; |
W |
|
= |
K4 |
; W = K |
|
; W ( p) = K |
|
; |
|||||||
|
1 |
p |
|
2 |
|
2 |
|
3 |
T3 p +1 |
|
|
4 |
|
p |
5 |
|
5 |
6 |
|
|
6 |
|
|||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
W7 ( p) = K7 ; W8 |
= |
|
K8 |
|
|
; W9 ( p) = K9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
T8 p +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Численные значения параметров передаточных функций: |
|
|
|
|
|||||||||||||||||||||
K1 = K2 = 0,5; K3 |
= 20; T3 |
= 0,2; K4 = K5 |
= 0,1; K6 = K7 = 1; K8 = 10; |
||||||||||||||||||||||
T8 = 2; K9 = 0,2. |
|
|
А |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Порядок выполнения работы |
|
|
|
|
|
|
|
||||||||||||
1. |
По структурной схеме модели линейной системы управления |
||||||||||||||||||||||||
построить граф системы. |
|
Д |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. Получить определитель графа системы. |
|
|
|
|
|
|
|
||||||||||||||||||
3. |
|
Определить все прямые пути графа системы от входа g до |
|||||||||||||||||||||||
выхода y и от возмущающего входа f до выхода y. |
|
|
|
|
|
|
|
||||||||||||||||||
4. |
|
Получить определители подграфов каждогоИпрямого пути от |
|||||||||||||||||||||||
входа g до выхода y и от возмущающего входа f до выхода y. |
|
|
|
|
|||||||||||||||||||||
5. |
|
По теореме Мейсона получить передаточную функцию сис- |
|||||||||||||||||||||||
темы управления Wyg относительно входа g и выхода y. |
|
|
|
|
|
|
|||||||||||||||||||
6. |
|
По теореме Мейсона получить передаточную функцию сис- |
|||||||||||||||||||||||
темы управления Wyf относительно возмущающего входа f и выхода y. |
|||||||||||||||||||||||||
8
7. Подставив численные значения параметров передаточных функций в полученные выражения, произвести упрощение и получить передаточные функции системы управления Wyg и Wyf в виде отношения стандартных полиномов.
8. Произвести моделирование исходной структурной схемы Смодели системы и полученных передаточных функций системы
управления Wyg и Wyf в Simulink [2, 6]. Произвести сравнение исходной и полученной модели по переходным и частотным характеристикам.
делать вывод о проведенных преобразованиях.
функций |
||
|
|
Содержание отчета |
1. |
Назван е цель ра оты. |
|
2. |
труктурная схема модели линейной системы управления. |
|
3. |
Передаточные функции системы и численные значения пара- |
|
метров передаточных |
. |
|
4. |
Граф модели л нейной системы управления. |
|
5. |
Формулы вычисления передаточных функций системы |
|
|
А |
|
управления Wyg и Wyf. |
|
|
6. |
Исходнаябструктурная схема модели линейной системы |
|
управления в обозначениях Simulink. |
||
7. |
Переходные и частотные характеристики исходной структур- |
|
ной схемы модели системы и полученных передаточных функций Д
системы управления Wyg и Wyf. 8. Выводы по работе.
Вопросы и задания для защиты лабораторной работы
1.Дайте определение графа модели системы управления.
2.Что отображает дуга и вершина на графе.
3.Поясните процедуру преобразования структурной схемы модели системы в граф.
4.Что называется прямым путём (контуром) графа модели системы управления?
5.Какие замкнутые контуры называются несоприкасающимися?
6.Что называется подграфом прямого пути?
7.Что такое определитель графа?
8.Как определяется передаточная функция системы управления по теореме Мейсона? И
9
Лабораторная работа № 2
Корневой критерий устойчивости линейной автоматической системы
Цель работы − изучить анализ устойчивости линейных автома-
СУстойч вость с стемы – это свойство системы возвращаться в исходный стац онарный режим при прекращении внешних воздействий на с стему. В автоматической системе управления это происхо-
тических систем управления корневым критерием.
дифференцприального уравнения, описывающего свободную составляющую дв жен я с стемы, заданных начальных условиях [1, 3, 8]
дит за счет зменен я внутренних переменных параметров системы. Оценкасвободнаяустойч вости представляет собой решение однородного
(a |
0 |
pn + a pn−1 +... + a |
)y = 0 при t → ∞. |
(2.1) |
|
1 |
n |
|
|
Если |
|
А |
|
|
|
составляющая выходного параметра системы |
|||
после прекращения внешнего воздействия стремится к нулю, то такая система является устойчивой. Другими словами, устойчивость систе-
мы это есть затухание ее переходных процессов.
Если свободная составляющая системы имеет вид гармонических колебаний с постоянной амплитудой, то система считается нейтральной (находится на границе устойчивости).
В том случае, если свободная составляющая неограниченно возрастает или имеет вид гармонических колебаний с возрастающей ам-
плитудой, то система считается неустойчивой. |
|
|
|
||||||
С целью упрощения анализаДустойчивости систем разработан |
|||||||||
ряд специальных методов, которые получили название |
критерии ус- |
||||||||
тойчивости, позволяющих оценить влияние параметров системы на |
|||||||||
её устойчивость. |
|
|
|
|
|
|
|
|
|
Математическая модель системы управления может быть при- |
|||||||||
ведена к общей передаточной функции [8] |
|
И |
|||||||
W ( p) = |
B( p) |
b pm +b pm−1 |
+b pm−2 |
+... +b |
(2.2) |
||||
A( p) |
= 0 |
1 |
2 |
pn−2 |
+... + a |
m , |
|||
|
a pn + a pn−1 |
+ a |
2 |
n |
|
||||
|
|
0 |
1 |
|
|
|
|
||
где B(p) = b0pm + b1pm-1 + b2pm-2 + … + bm – полином числителя, А(p) = a0pn + a1pn–1 + a2pn–2 + … + an – полином знаменателя.
10
Характеристикой системы, описывающей свободную составляющую движения системы, является характеристический полином, находящийся в знаменателе передаточной функции, а вынужденную составляющую движения системы – полином, находящийся в числи-
теле передаточной функции. |
|
|||
С |
|
|
|
|
Путём приравнивания характеристического полинома А(p) к ну- |
||||
лю можно получить характеристическое уравнение системы [8]: |
|
|||
|
a0pn + a1pn–1 + a2pn–2 + … + an = 0. |
(2.3) |
||
Корни характер |
стического уравнения pi могут быть представ- |
|||
Корни |
|
|||
лены комплексными ч слами вида [8]: |
|
|||
|
|
pi = α ± jβ = Re(pi) ± jIm(pi). |
(2.4) |
|
пол нома числителя B(p) называют нулями, а корни по- |
||||
б |
|
|||
линома знаменателя |
А(p) – полюсами передаточной функции системы. |
|||
Расположен е нулей |
полюсов определяется типом передаточной |
|||
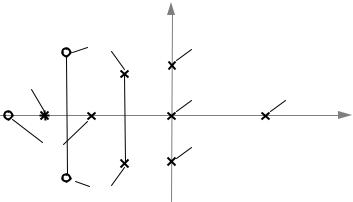
функц с стемы. Полюсы на комплексной плоскости изображают символом «×», а нули – символом «о». Их совместное изображение
|
А |
|
||
называют картой (д аграммой) нулей и полюсов (рис. 2.1). |
||||
|
|
Im |
|
|
|
4 |
5 |
|
|
6 |
|
Д |
||
|
|
3 |
1 |
|
|
2 |
0 |
5 |
Re |
|
|
|
|
|
|
4 |
|
Рис. 2.1. Карта нулей и полюсов системы на комплексной плоскости |
||
Виды корней нулей и полюсов линейной системы управления: |
||
Действительные: |
|
И |
•положительные (1);
•отрицательные (2);
•нулевые (3).
Комплексные:
•комплексные сопряженные (4);
•чисто мнимые (5).
11
По кратности корни бывают:
•одиночные (1, 2, 3);
•сопряженные (4, 5): pi = α ± jβ;
•кратные (6) pi = pi +1 = ….
Корневой критерий определяет необходимое условие устойчи- Свости системы по виду передаточной функции системы или её харак-
теристическому уравнению.
Корневой кр тер й устойчивости. Для устойчивости линейной системы необход мо, чтобы все корни характеристического уравнения (полюса) с стемы лежали в левой полуплоскости комплексной
плоскости, т. е. α < 0. В данном случае система имеет затухающие
колебан я переходного процесса [1, 3, 8]. |
|
|
|
|
|||||||
|
хотя |
ы од н полюс находится на мнимой оси (α = 0), то |
|||||||||
|
б |
|
|
|
|
||||||
говорят, что с стема находится на границе устойчивости, переходный |
|||||||||||
процесс будет незатухающим с постоянной амплитудой. |
|
||||||||||
Еслихотя ы од н полюс находится в правой полуплоскости |
|||||||||||
(α > 0), то с стема является неустойчивой и имеет расходящийся |
|||||||||||
|
|
А |
|
|
|||||||
переходный процесс. |
|
|
|
|
|
|
|
|
|
||
Пример. Передаточная функция линейной системы управления |
|||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( p) = |
|
|
|
3p +4 |
|
. |
|
(2.5) |
|
|
|
p |
3 |
+2 p |
2 |
+2,25 p +1,25 |
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Д |
|
|||||
Характеристическое уравнение числителя передаточной функ- |
|||||||||||
ции 3p + 4 = 0. |
|
|
|
|
|
|
|
|
|
|
|
Характеристическое |
уравнение |
знаменателя |
передаточной |
||||||||
функции: p3 + 2p2 + 2,25p + 1,25 = 0. |
|
И |
|||||||||
Для вычисления нулей и полюсов системы и изображения их |
|||||||||||
карты можно |
применить |
специальный |
инструмент |
Simulink про- |
|||||||
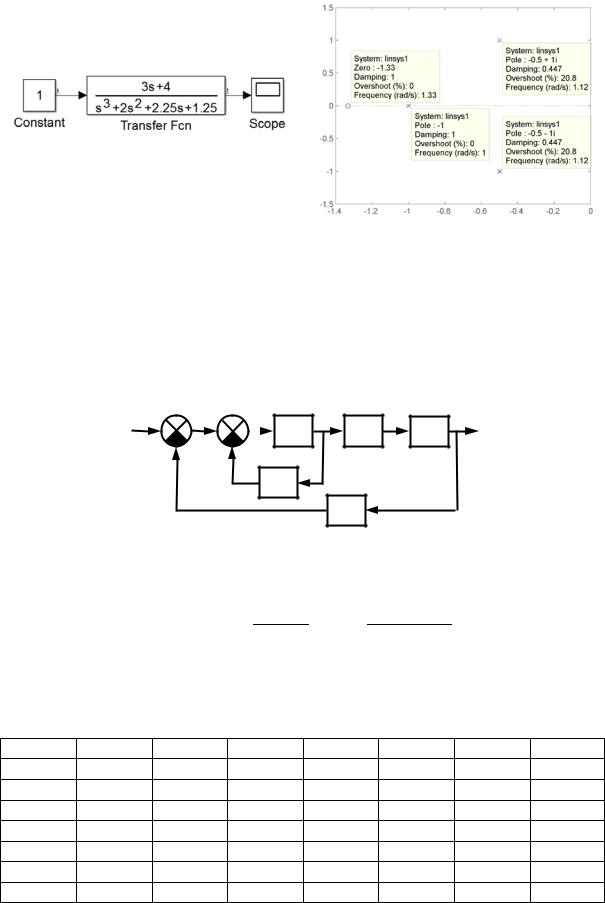
граммного комплекса Matlab [2, 6]. Для получения нулей и полюсов системы необходимо задать точки входа и выхода модели системы для линеаризации: «Input point» и «Output point». Выполнить команду меню модели Simulink: Analysis > Control Design > Linear Analysis,
после выбрать характеристику «New Pole/Zero Map» и запустить процесс линеаризации модели (рис. 2.2).
«Нули» системы: p1 = – 1,33.
«Полюса» системы: p1 = – 1; p2 = – 0,5 + j; p3 = – 0,5 – j.
Все действительные части полюсов отрицательны, следовательно, система устойчива.
12
|
|
а |
|
|
|
б |
|
|
|
|
|
|
Рис. 2.2. Нахожден е корней характеристического уравнения системы в Simulink: |
||||||||||||
Са – структурная схема |
; – карта нулей и полюсов в Simulink |
|||||||||||
|
Исходные данные для выполнения работы |
|
|
|||||||||
На р с. 2.3 представлена структурная схема модели линейной |
||||||||||||
модели |
|
|
|
|
|
|
||||||
системы управлен я. |
|
|
|
|
|
|
|
|
|
|||
|
|
g |
|
|
|
W1 |
W3 |
W4 |
y |
|
|
|
|
|
+ |
|
|
+ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
б– – |
|
|
|
|
|
||||||
|
|
|
|
y |
W2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W5 |
|
|
|
|
|
Рис. 2.3. СтруктурнаяАсхема модели линейной системы управления |
||||||||||||
Передаточные функции системы управления: |
|
|
|
|||||||||
W |
= K1 ; |
W = K |
|
; W = |
K3 |
; W = |
|
K4 |
; W = K |
|
. |
|
1 |
p |
2 |
|
2 |
3 |
T3 p +1 |
4 |
p(T4 p +1) |
5 |
5 |
|
|
|
|
|
|
|
|
Д |
||||||
В табл. 2.1 приведены численные значения параметров переда- |
||||||||||||
точных функций системы управления: |
|
|
Таблица 2.1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
№ вар. |
K1 |
|
K2 |
K3 |
T3 |
|
K4 |
T4 |
|
K5 |
||
1 |
10 |
|
0,5 |
2 |
0,2 |
|
И |
|||||
|
|
0,2 |
2 |
|
0,8 |
|||||||
2 |
12 |
|
0,2 |
0,1 |
0,5 |
|
0,5 |
0,5 |
|
1 |
||
3 |
5 |
|
1 |
|
5 |
0,5 |
|
0,1 |
1 |
|
1,5 |
|
4 |
15 |
|
0,5 |
10 |
1 |
|
0,1 |
1 |
|
1 |
||
5 |
15 |
|
0,1 |
0,2 |
2 |
|
0,2 |
1 |
|
1,5 |
||
6 |
0,1 |
|
0,1 |
5 |
2 |
|
0,1 |
2 |
|
1 |
||
7 |
2 |
|
1 |
|
2 |
2 |
|
0,1 |
2 |
|
0,5 |
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
Порядок выполнения работы |
|
1. |
Составить структурную схему модели линейной системы |
|
управления в Simulink. |
|
|
2. |
помощью инструмента Linear Analysis получить карта ну- |
|
С |
|
|
лей и полюсов системы управления. |
||
3. |
Определить тип корней характеристического уравнения сис- |
|
темы управления. |
|
|
4. |
Пользуясь корневым критерием устойчивости, сделать вывод |
|
об устойч вости с стемы управления. |
||
функции |
||
|
|
Содержание отчета |
1. |
Назван е цель ра оты. |
|
2. |
Структурная схема модели линейной системы управления. |
|
3. |
Передаточные |
системы и численные значения пара- |
метров передаточных функций. |
||
4. |
Структурная схема модели линейной системы управления в |
|
|
А |
|
обозначениях Simulink. |
|
|
5. |
Картабнулей и полюсов системы управления в Simulink. |
|
6. |
Значения нулей и полюсов системы управления. |
|
7. |
Выводы об устойчивости системы управления. |
|
Вопросы и задания для защиты лабораторной работы
1.Определение устойчивости системы и её математическая интерпретация.
2.Что такое передаточная функция системы?
3.Как найти характеристическое уравнение системы?
4.Назовите типы корней характеристического уравнения.
5.Чем определяется количество корней характеристического уравнения?
6.Сформулируйте критерий устойчивости по корням характеристического уравнения.
7.Что является нулями и полюсами системы управления?
8.Что является картой нулей и полюсов системы управления?ДИ
14
Лабораторная работа № 3
Исследование робастной устойчивости линейной автоматической системы
СИсследован устойчивости систем управления при наличии не- в х параметров является весьма важным и актуаль-
Цель работы − изучить анализ робастной устойчивости линей-
ных автоматических систем управления методом Харитонова.
Общие сведения
ным направлен ем научных исследований, так как позволяет, на этапе проект рован я, определить, является ли устойчивой система при
безопасное отвечать устойчивомуАповедению этого объекта, так как они принад-
изменен |
её параметров в процессе эксплуатации. Это позволяет |
обеспеч ть |
функционирование управляемого объекта, не- |
определенности |
|
смотря на то, что в процессе изготовления и эксплуатации его пара- |
|
метры хотя |
могут отл чаться от расчётных, но гарантировано будут |
лежат области ро астной устойчивости.
Робастная устойчивость системы – это динамическая устой-
чивость системы при изменении внутренних переменных параметров
системы в некотором диапазоне [3, 4]. |
|
Д |
|
При анализе робастной устойчивости также применяются при- |
|
кладные математические методы. |
|
Рассмотрим характеристический полином системы управления: |
|
А(p) = a0pn + a1pn–1 + a2pn–2 + … + an = 0. |
(3.1) |
Введем в рассмотрение (п + 1)-мерный векторИ{а} = (a0 a1, ..., ап). Пусть в (п + 1)-мерном пространстве коэффициентов задано множест-
во {А}. Полином А(p) называется робастно устойчивым или робаст-
но устойчивым на множестве {А}, если он является устойчивым (т. е. все его полюса являются левыми) при любых значениях коэффици-
ентов аi (i = 0, 1, ..., п) из множества {А} ({а} {А}). Система называ-
ется робастно устойчивой или робастно устойчивой на множестве
{А}, если её характеристический полином является робастно устойчивым полиномом на множестве {А}.
15
Полиномы Харитонова. Пусть множество {А} является гиперпараллелепипедом [3, 4]:
|
|
|
|
|
|
|
|
|
|
|
|
|
{A}= {a : ai ≤ ai |
≤ |
|
i }, i = 0, 1, ..., п, |
|
|
|
|
|
|
(3.2) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||||||||||||||||||||
где ai и |
|
|
|
i – минимальные и максимальные значения коэффициентов |
||||||||||||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||||||||||
аi (i = 0, 1, ..., п). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Полиномы А1(p), |
А2(p), А3(p), и А4(p), со следующими коэффици- |
||||||||||||||||||||||||||||||||||||||||
ентами (коэффициенты выписаны в порядке убывания индексов) |
|
|||||||||||||||||||||||||||||||||||||||||
A |
(р)= |
a |
n |
+a |
n−1 |
p +a |
n−2 |
p2 |
+ |
a |
n−3 p3 |
+ |
a |
n−4 p4 +a |
n−5 |
p5 |
+a |
n−6 |
p6 |
...; |
(3.3) |
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
номами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
A |
(р) |
= |
a |
n |
+ |
a |
n−1 p +a |
n−2 |
p2 |
+a |
n−3 |
p3 |
+ |
a |
n−4 p4 + |
a |
n−5 p5 +a |
n−6 |
p6 |
...; |
(3.4) |
|||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
(р) |
= a |
n |
+ |
a |
n−1 p + |
a |
n−2 p2 +a |
n−3 |
p3 |
+a |
n−4 |
p4 + |
a |
n−5 p5 |
+ |
a |
n−6 p6 |
...; |
(3.5) |
||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
(р) |
= a |
|
+a |
|
p +an−2 p2 + |
|
n−3 p3 |
+a |
|
p4 +a |
|
p5 |
+ |
|
n−6 p6 |
...; |
(3.6) |
||||||||||||||||||||||||
n |
n−1 |
a |
n−4 |
n−5 |
a |
|||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
называются пол |
|
|
|
Харитонова. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Необход мое условие ро астной устойчивости. Так как при ро- |
|||||||||||||||||||||||||||||||||||||||||
бастной устойч вости в параллелепипеде (3.2) должны быть устойчи- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
||||||||||||||||||||||
выми характеристическиебполиномы при всех значениях коэффициентов из этого параллелепипеда, необходимо, чтобы был устойчивым характеристический полином при минимальных значениях коэффи-
циентов ai (i = 0, 1, ..., п). Поэтому для робастной устойчивости системы управления на множестве { }, согласно критерию А. Стодолы, необходимо, чтобы все минимальныеДзначения коэффициентов аi бы-
ли положительными (ai > 0, i = 0, 1, ..., п) [3, 4].
Теорема Харитонова. Для того чтобы система управления с характеристическим полиномом (p) (3.1) была робастно устойчива на множестве {А} (3.2), необходимо и достаточноИ, чтобы все полиномы Харитонова были устойчивыми [3, 4].
В случае, когда п = 1, 2, 3, 4, 5, нет необходимости проверять устойчивость всех четырёх полиномов Харитонова.
При n = 1 и 2 необходимое условие робастной устойчивости является и достаточным.
В случае выполнения необходимого условия при n = 3, 4 и 5, достаточным условием робастной устойчивости является:
а) при п = 3 – устойчивость полинома А1(p);
б) при п = 4 – устойчивость полиномов А1(p) и А2(p);
в) при п = 5 – устойчивость полиномов А1(p), А2(p) и А3(p).
16
Пример. Исследовать робастную устойчивость системы, ха-
рактеристический полином которой имеет вид |
|
|||||||
А(p) = p4 + 3p3 + a2p2 + a3p + a4. |
(3.7) |
|||||||
При изменении следующих параметров полинома: |
|
|||||||
4 ≤ a2 ≤ 5; 2 ≤ a3 ≤ 3; 1 ≤ a4 ≤ 2. |
|
|
|
|
|
|||
Запишем множество {А} по (3.2): |
|
|
|
|
|
|||
{A}= {a : a0 =1;a1 = 3;4 ≤ a2 ≤ 5;2 ≤ a3 ≤ 3;1 ≤ a4 ≤ 2;}. |
(3.8) |
|||||||
Так как n = 4 выполняется необходимое условие робастной ус- |
||||||||
тойчивости, достаточно рассмотреть полиномы Харитонова А1(p) и А2(p). |
||||||||
матрицы Гурв ца для н х удут иметь размер 4х4. |
|
|||||||
СА1(p) = p4 + 3p3 |
+ 4p2 |
+ 2p + 2; |
(3.9) |
|||||
А2(p) = p4 + 3p3 + 4p2 + 3p + 2. |
(3.10) |
|||||||
б |
|
|
|
|
||||
Устойч вость полиномов Харитонова проверяем по критерию |
||||||||
Гурвица. Поскольку степень полиномов Харитонова n равна 4, то |
||||||||
Матр цы Гурв ца для |
1(p) и |
2(p): |
|
|
|
|
||
А |
|
|||||||
|
|
3 |
2 |
0 |
0 |
|
|
|
|
|
1 |
4 |
2 |
0 |
|
|
(3.11) |
∆ 1 = |
0 |
3 |
2 |
0 |
. |
|||
|
|
|
|
|
||||
|
|
0 |
1 |
4 |
2 |
|
|
|
|
|
|
|
|
||||
|
3 |
3 |
0 |
0 |
|
|
||
|
|
1 |
4 |
2 |
0 |
|
|
|
∆ |
|
|
|
(3.12) |
||||
2 = |
|
|
|
|
. |
|||
|
|
0 |
3 |
3 |
0 |
|
И |
|
|
|
0 |
1 |
4 |
2 |
|
||
|
|
|
|
|
|
|
||
Диагональные миноры матрицыДА1: |
|
|||||||
1 = 3 > 0; 2 = 10 > 0; 3 = 2 > 0; 4 = 4 > 0. |
|
|||||||
Диагональные миноры матрицы |
А2: |
|
|
|
||||
1 = 3 > 0; 2 = 9 > 0; 3 = 9 > 0; 4 = 18 > 0.
Поскольку все определители положительны, то полиномы Харитонова устойчивы, и, соответственно, система управления робастно устойчива в заданном диапазоне параметров.
17
|
|
Исходные данные для выполнения работы |
|||||||
вид |
Передаточная функция разомкнутой системы управления имеет |
||||||||
|
|
|
|
b0 p +b1 |
|
|
|
|
|
|
|
W ( p) = |
|
|
|
|
|
. |
|
|
|
p4 |
+ a p3 + a p2 + a p + a |
||||||
С |
1 |
2 |
3 |
|
4 |
|
|||
|
Исследовать робастную устойчивость замкнутой системы |
||||||||
управлен я при следующих значениях параметров: |
|
|
|||||||
1) |
2 |
≤ a1 ≤ 3; 3 ≤ a2 ≤ 4; 1,5 |
≤ a3 ≤ 2,5; 0,1 ≤ a4 |
≤ 0,2; b0 = 1; b1 = 0,5; |
|||||
и |
|
|
|
|
|
||||
2) |
3 |
≤ a1 ≤ 4; 10 ≤ a2 ≤ 15; 0,5 ≤ a3 |
≤ 1; 1,2 ≤ a4 ≤ 1,4; b0 = 2; b1 = –1; |
||||||
3) |
1 |
≤ a1 ≤ 4; 7 ≤ a2 ≤ 9; 1,5 |
≤ a3 ≤ 2,5; 0,5 ≤ a4 |
≤ 1; b0 = –1; b1 = 0,5; |
|||||
4) |
1 |
≤ a1 ≤ 2; 8 ≤ a2 ≤ 9; 0,5 ≤ a3 ≤ 1; 1,5 ≤ a4 ≤ 2; b0 = 1; b1 = –1; |
|||||||
5) |
2 |
≤ a1 ≤ 3; 6 ≤ a2 ≤ 8; 1 ≤ a3 ≤ 2; 0,1 ≤ a4 ≤ 0,5; b0 = b1 = 0,5; |
|||||||
|
|
б |
|
|
|
|
|||
6) |
0,5 ≤ a1 ≤ 1; 5 ≤ a2 ≤ 6; 1 |
≤ a3 ≤ 3; 0,2 ≤ a4 |
≤ 0,4; b0 = –0,5; b1 = 0,4; |
||||||
7) |
0,6 ≤ a1 ≤ 0,8; 4 ≤ a2 ≤ 5; |
2 ≤ a3 |
≤ 4; 0,3 ≤ a4 |
≤ 0,7; b0 = –1; b1 = 0,2; |
|||||
8) |
0,9 ≤ a1 ≤ 1,5; 3 ≤ a2 ≤ 5; 0,2 ≤ a3 ≤ 0,5; 0,5 ≤ a4 ≤ 1; b0 = b1 = 0,5; |
||||||||
9) |
5 |
≤ a1 ≤ 6; 2,5 ≤ a2 ≤ 3,5; |
3 ≤ a3 |
≤ 4; 2,5 ≤ a4 |
≤ 3; b0 = b1 = –1,5; |
||||
|
|
А |
|||||||
10) |
4 |
≤ a1 ≤ 5; 3,5 ≤ a2 ≤ 4; 2,5 ≤ a3 |
≤ 4,5; 3 ≤ a4 |
≤ 4; b0 = –2; b1 = –2,5. |
|||||
Порядок выполнения работы
1.Записать передаточную функцию и характеристический полином замкнутой системы управления.
2.Записать диапазон изменения параметров в виде множества
{А}.
3.Записать полиномы Харитонова.
4.Пользуясь теоремой Харитонова проанализировать робастную устойчивость системы управления.Д
Содержание отчетаИ
1.Название и цель работы.
2.Передаточная функция и характеристический полином замкнутой системы управления. Диапазоны изменения параметров системы.
3.Полиномы Харитонова
4.Выводы об устойчивости системы управления.
18
Вопросы и задания для защиты лабораторной работы
1. |
Определение робастной устойчивости системы. |
2. |
Что такое передаточная функция системы? |
3. |
Что представляют собой полиномы Харитонова? |
С |
|
4. |
Необходимое условие робастной устойчивости. |
5. |
Расскажите теорему Харитонова. |
6. |
Как проверяется устойчивость полиномов Харитонова? |
и |
|
|
б |
|
А |
|
Д |
|
И |
19
Лабораторная работа № 4
Исследование качества регулирования линейной автоматической системы
СЦель работы − изучить методы анализа качества регулирования
линейных автоматических систем управления по прямым и косвенным показателям качества.
Общие сведения
о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям.
точностиЕсли сследуемая АСР устойчива, то может возникнуть вопрос
В общем случае качество регулирования представляет собой со-
вокупность |
в установившемся режиме и качества переход- |
ных процессов в переходном режиме. |
|
При |
сследован качества переходного процесса принято ис- |
|
А |
пользовать единичное ступенчатое воздействие 1(t). |
|
В результатебоценки качества регулирования точными числен- |
|
ными методами получают применение параметры переходного про-
цесса, называемые показателями качества [1, 3, 7, 8].
Показатели качества могут быть прямыми и косвенными. В свою очередь они могут быть статическими и динамическими. Динамические показатели характеризуют переходной процесс, а статические – установившийся режим.
К основным прямым показателям качества относятся [1, 3, 7, 8]: |
|||
• tP – время регулирования (время переходного процесса); |
|||
• tн – время нарастания; |
Д |
||
|
И |
||
• |
σ – перерегулирование; |
|
|
• |
μ – колебательность; |
|
|
• ψ – степень затухания; |
|
||
• |
СТ – статическая ошибка. |
||
Время регулирования – интервал времени от подачи единичного ступенчатого воздействия x(t) = 1(t) на вход системы до момента, когда отклонение переходной характеристики h(t) от установившегося зна-
чения hУСТ не превышает некоторой заданной величины q. Значение интервала q выбирают обычно равное 2 % или 5 % от величины hУСТ.
20
Колебательность – отношение двух соседних максимальных положительных отклонений переходной характеристики от установившегося hУ Т или заданного hЗАД значения, часто выражается в процентах:
µ = hmax2 − hУСТ |
100 % . |
(4.1) |
|
h |
− h |
|
|
max1 |
УСТ |
|
|
Перерегулирование – это отношение первого максимального положительного отклонения переходной характеристики от установив-
шегося hУ Т |
ли заданного hЗАД |
значения к установившемуся или за- |
|||||
данному значен ю, выраженное в процентах: |
|
||||||
С |
σ = |
hmax1 |
− hУСТ |
100 % . |
(4.2) |
||
|
|
|
|
hУСТ |
|
|
|
тат ческая ош ка – разница между заданным и установив- |
|||||||
значен ем регул руемой величины: |
|
||||||
шимся |
= hЗ Д −hУСТ . |
(4.3) |
|||||
|
|
∆СТ |
|||||
Оценка качества регулирования по корневым показателям ос- |
||||||
нована на анализе значений действительной Re(pi) и мнимой Im(pi) |
||||||
части корнейбpi характеристического уравнения системы. К корневым |
||||||
показателям качества относятся [1, 3, 7, 8]: |
|
|||||
• η – степень устойчивости – критерий длительности переход- |
||||||
ного процесса; |
|
|
|
|
|
|
• m – степень колебательности – критерий колебательности пе- |
||||||
реходного процесса. |
А |
|
||||
|
Д |
|
||||
Степень устойчивости η определяется как граница, правее ко- |
||||||
торой корней нет, или минимальное абсолютное значение действи- |
||||||
|
|
|
|
И |
||
тельной части Re(pi) корней характеристического уравнения системы: |
||||||
|
η = min |
Re( pi ) |
= min |
αi |
. |
(4.4) |
Геометрически η равно расстоянию от оси мнимых значений до ближайшего корня и служит мерой удаления системы от границы устойчивости, которой в комплексной плоскости является мнимая ось.
Степень колебательности m определяется как максимальное абсолютное значение отношения мнимой к действительной части
корней характеристического уравнения системы: |
|
|||||||||
m = max |
|
Im( pi ) |
|
= max |
|
βi |
|
. |
(4.5) |
|
|
|
|
|
|||||||
|
|
Re( p ) |
|
|
|
α |
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
21
Геометрически m равен тангенсу максимального абсолютного |
|||||||||||
значения угла γ между лучом, проведенным из начала координат че- |
|||||||||||
рез корень, и осью действительных значений. |
|
||||||||||
Таким образом, при всех прочих условиях, качество регулиро- |
|||||||||||
вания будет тем лучше, чем больше степень устойчивости η и меньше |
|||||||||||
степень колебательности m. |
|
|
|
|
|
|
|
||||
Длительность отдельных составляющих переходного процесса |
|||||||||||
пропорц ональна |
х постоянным времени затухания, и обратно про- |
||||||||||
порциональна абсолютному значению действительной части Re(pi) |
|||||||||||
определяющ х х корней характеристического уравнения системы. |
|||||||||||
Так м образом, |
длительность всего переходного процесса будет |
||||||||||
С |
|
|
устойчивости [1, 3, 7, 8]: |
|
|||||||
определяться по |
|
|
|
||||||||
|
|
|
|
|
|
tP ≈ |
3 . |
|
|
(4.6) |
|
|
|
|
|
|
|
|
|
η |
|
|
|
Между коле ательностью переходной характеристики μ и кор- |
|||||||||||
степени |
|
|
|
|
|
|
|||||
невым показателем коле ательности m существует связь [1, 3, 7, 8] |
|||||||||||
|
|
|
|
|
|
µ ≈ e |
−2π |
. |
|
(4.7) |
|
|
|
|
|
|
|
m |
|
||||
б |
|
|
|||||||||
Исходные данные для выполнения работы |
|
||||||||||
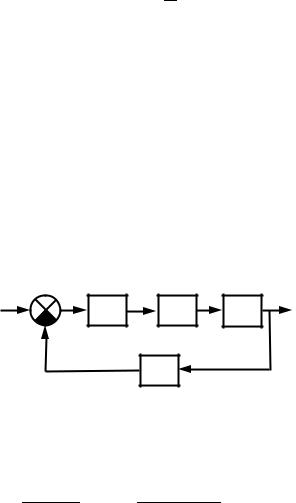
На рис. 4.1 представлена структурная схема модели линейной |
|||||||||||
|
А |
|
|||||||||
системы управления. |
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
W1 |
|
|
W2 |
|
y |
|
|
+ |
|
|
|
|
|
|
W3 |
|
||
|
–y |
|
|
|
|
Д |
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
W4 |
|
|
|
|
Рис. 2.3. Структурная схема модели линейной системы управления |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
И |
|
Передаточные функции системы управления: |
|
||||||||||
W1 = K1 ; W2 = |
|
K2 |
|
; |
W3 |
= |
|
K3 |
; W4 = K4 . |
|
|
T2 p +1 |
p(T3 p +1) |
|
|||||||||
|
|
|
|
|
|
||||||
В табл. 4.1 приведены численные значения параметров переда- |
|||||||||||
точных функции системы управления. |
|
|
|
||||||||
22

|
|
|
|
|
|
|
|
|
Таблица 4.1 |
|
|
|
|
|
|
|
|
|
|
|
№ вар. |
K1 |
K2 |
T2 |
|
K3 |
|
T3 |
K4 |
|
1 |
2 |
0,05 |
0,5 |
|
10 |
|
1 |
0,95 |
|
2 |
5 |
0,02 |
0,2 |
|
10 |
|
2 |
1,5 |
|
3 |
10 |
0,01 |
0,1 |
|
10 |
|
5 |
1 |
С |
0,5 |
0,2 |
|
10 |
|
1 |
1 |
||
4 |
5 |
|
|
||||||
|
5 |
3 |
1 |
0,05 |
|
2 |
|
10 |
0,8 |
|
6 |
1 |
5 |
0,02 |
|
5 |
|
5 |
1 |
|
7 |
2 |
1 |
0,1 |
|
10 |
|
3 |
0,5 |
|
8 |
4 |
2 |
0,2 |
|
6 |
|
2 |
1 |
|
и |
|
|
|
|
|
|
||
9 |
1 |
1 |
0,1 |
|
2 |
|
1 |
2 |
|
|
10 |
0,5 |
0,5 |
0,1 |
|
6 |
|
0,5 |
1 |
|
|
Порядок выполнения работы |
|
|
|||||
|
|
б |
|
|
|
|
|||
|
1. Состав ть структурную схему модели линейной системы |
||||||||
|
управлен я в Simulink [2, 6]. |
|
|
|
|
|
|
||
2. |
С помощью |
нструмента Linear Analysis получить карта ну- |
|||||||
|
|
|
А |
|
|
||||
|
лей и полюсов системы управления. |
|
|
|
|
||||
3. |
Определить по корням характеристического уравнения сис- |
||||||||
темы корневые показатели качества системы управления.
4. Определить длительность переходного процесса и колеба-
тельность системы управления по степени устойчивости и степени |
|
колебательности. |
Д |
|
|
5. Получить с помощью инструмента Linear Analysis время регулирования и колебательность системы управления напрямую с переходной характеристики.
6. Сравнить показатели качества, полученные прямым и кос- |
|
венным способом. Сделать вывод. |
И |
|
|
Содержание отчета
1.Название и цель работы.
2.Структурная схема модели линейной системы управления.
3.Передаточные функции системы и численные значения параметров передаточных функций.
4.Структурная схема модели линейной системы управления в обозначениях Simulink.
5.Карта нулей и полюсов системы управления в Simulink.
6.Значения нулей и полюсов системы управления.
23
7. |
Значения степени устойчивости и степени колебательности |
|
системы управления. |
|
|
8. |
Значения показателей качества регулирования, полученных |
|
прямым и косвенным методом. |
||
9. |
Выводы о соответствии показателей качества, полученных |
|
С |
|
|
прямым и косвенным методом. |
||
Вопросы задания для защиты лабораторной работы |
||
1. |
Что представляет собой качество регулирования? |
|
регулирован |
||
2. |
Как воздействия на АСР применяют при оценке качества |
|
|
я? |
|
3. |
По как м характеристикам определяются прямые и косвен- |
|
ные показатели качества? |
||
4. |
Определен |
времени регулирования системы. |
5. |
Определен |
коле ательности системы. |
6. |
Определен е перерегулирования системы. |
|
7. |
Как е существуют корневые показатели качества и как их |
|
определить? |
А |
|
8. |
Запишитебсвязь между прямыми и косвенными показателями |
|
качества регулирования. |
||
|
|
Д |
|
|
И |
24
Лабораторная работа № 5
Вычисление интегральных показателей качества регулирования линейной системы
Цель работы − изучить методы анализа качества регулирования линейных автоматических систем управления с помощью интеграль-
ной квадрат чной оценки. |
|
||
С |
Общие сведения |
||
|
|||
Как |
звестно, качество регулирования в автоматических систе- |
||
мах управлен я оцен вается совокупностью показателей. Зачастую |
|||
изменен |
параметров системы с целью обеспечения требуемых |
||
характер |
ст |
к переходного процесса одни из показателей улучшают- |
|
при ся, в то времябкак друг е ухудшаются. В такой ситуации, когда задача
выбора опт мальных значений параметров системы оказывается многокритер альной, а потому трудноразрешимой, использование интегральных критериев, оценивающих качество регулирования одним числом, оказывается предпочтительным.
Интегральные оценки дают обобщенную оценку быстроты зату-
хания и величины отклонения регулируемой координаты, в виде еди- |
|||
ного числового значения. Особенность интегральной оценки в том, |
|||
что в отличии от других методов оценки качества, величина интегра- |
|||
А |
|
||
ла представляет число, которое ничего не говорит о характере пере- |
|||
ходного процесса, о конкретных показателях качества, зато, в сравне- |
|||
нии с другими, метод отличается простотой [1, 3, 4]. |
|
||
Простейшей линейной интегральной оценкой может служить ве- |
|||
личина [1, 3, 4]: |
Д |
|
|
|
|
|
|
∞ |
∞ |
[y(∞) − y(t)]dt , |
|
J1 = ∫e(t)dt = ∫ |
(5.1) |
||
0 |
0 |
И |
|
|
|
||
где e(t) = y(∞) – y(t) есть отклонение выходной величины от нового установившегося значения y(∞), которое она будет иметь после завершения переходного процесса.
В устойчивой системе e(t) → 0 при t → ∞ и этот интеграл имеет конечную величину. Геометрическим смыслом линейной интегральной оценки будет площадь под кривой, построенной для отклонения e(t) (рис. 5.1, а).
25
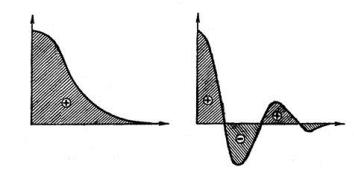
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.
С |
|
|
e |
|
e |
а |
|
б |
|
|
e(t) |
|
|
e(t) |
ческий |
t |
|
t |
|
|
|
|
||
Р с. 5.1. Геометр |
смысл линейной интегральной оценки: |
|||
б |
||||
а – монотонный переходный процесс; |
|
– колебательный переходный процесс |
||
Неудобством л нейной интегральной оценки вида является то, что она год тся только для монотонных процессов, когда не меняется знак отклонен я e(t). Если же имеет место колебательный процесс (рис. 5.1, б), то при Авычислении интеграла (5.1), площади подынтегральной кривой удут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания.
В связи с этим наибольшее распространение при анализе качества регулирования в автоматических системах управления получила
интегральная квадратичная оценка [1, 3, 4]:
∞ |
∞ |
2 |
|
J2 = ∫e2 (t)dt |
= ∫ |
[y(∞) − y(t)] dt , |
(5.2) |
0 |
0 |
И |
|
Величина J2 будет тем меньшеД, чем меньше сумма площадей, |
|||
взятых для квадратов ординат |
подынтегральной кривой, |
т. е. чем |
|
лучше переходный процесс приближается к идеальному скачку управляемой величины вслед за скачком задающего или возмущающего воздействия.
Прямое вычисление переходной характеристики y(t) при входном воздействии на систему g(t) = 1(t) довольно затруднительно, особенно при высоком порядке передаточной функции замкнутой системы W(p). Поэтому пользуются операторным представлением функций.
Тогда единичное ступенчатое воздействие на систему g(t) = 1(t) в операторной форме можно представить выражением:
26

|
|
|
|
G( p) = L[1(t)]= |
1 . |
|
|
|
(5.3) |
||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
Переходная характеристика системы y(t) при входном воздейст- |
|||||||||||||||
вии на систему G(p) = 1/p в операторной форме: |
|
|
|||||||||||||
|
|
|
Y ( p) = L[y(t)]= W ( p) . |
|
|
(5.4) |
|||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
Установ вшееся значение y(∞) выходной величины в оператор- |
|||||||||||||||
ной форме при входном воздействии на систему G(p) = 1/p можно оп- |
|||||||||||||||
ределить как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
1 |
limW ( p). |
|
(5.5) |
||
Y (∞) = L[y(∞)]= y(∞) = |
|
||||||||||||||
|
|
|
|
|
|
|
|
p |
|
p p→0 |
|
|
|||
Отклонен я |
вел |
|
|
|
от установившегося значения e(t) |
при |
|||||||||
входном воздейств |
|
на систему G(p) = 1/p в операторной форме: |
|
||||||||||||
чины |
|
|
|
|
|
|
|
|
|
||||||
E( p) = L[e(t)]= L[y(∞)]− L[y(t)]=Y (∞) −W ( p) . |
(5.6) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
Если E(jω) есть изо ражение Фурье функции времени e(t), то, |
|||||||||||||||
б |
|
|
|
|
|
|
|||||||||
согласно теореме Парсеваля, интегрирование функции по времени в |
|||||||||||||||
пределах от нуля до |
есконечности можно заменить интегрированием |
||||||||||||||
модуля изображения Фурье этой функции по всем частотам ω. |
|
||||||||||||||
∞ |
|
2 |
|
|
|
|
∞ |
|
2 |
|
|
∞ |
2 |
|
|
J2 = ∫e |
А1 1 |
dω; |
(5.7) |
||||||||||||
|
(t)dt = |
2π |
|
∫ |
E( jω) |
dω = |
π |
∫ E( jω) |
|||||||
0 |
|
|
|
|
|
−∞ |
|
|
|
|
0 |
|
|
||
E( jω) = y(∞) |
−W ( jω) |
= y(∞) −W ( jω) . |
(5.8) |
||||||||||||
|
|
|
|
jω |
|
|
jω |
|
|
|
|
jω |
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||
Пример. На рис. 5.2 представлена структурная схема модели ли- |
|||||||||||||||
нейной системы управления. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
g |
|
|
|
|
W1 |
|
W2 |
|
|
y |
|
|
|
|
|
+ |
|
–y |
|
|
|
|
И |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
W3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.2. Структурная схема модели линейной системы управления |
|
||||||||||||||
27

Передаточные функции системы управления: |
|
|
|
|
|
||||||||||||||||||||||||||
W ( p) =10 ; |
W ( p) |
= |
|
|
0,5 |
|
|
|
; W |
|
( p) =1,5. |
|
|
|
|
|
|||||||||||||||
|
(2 p +1)p |
|
|
|
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Требуется вычислить интегральную квадратичную оценку J2. |
|||||||||||||||||||||||||||||||
Передаточная функция замкнутой системы W(p): |
|
|
|
|
|||||||||||||||||||||||||||
|
W ( p) = |
|
|
W1( p)W2 ( p) |
|
|
|
|
|
= |
|
|
5 |
|
. |
|
(5.9) |
||||||||||||||
|
1 +W ( p)W ( p)W ( p) |
2 p2 + p +7,5 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходная характеристика системы y(t) при входном воздейст- |
|||||||||||||||||||||||||||||||
значени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вии на с стему G(p) = 1/p в операторной форме: |
|
|
|
|
|
||||||||||||||||||||||||||
СY ( p) = W ( p) |
= |
|
|
|
|
|
5 |
|
|
|
|
1 |
. |
|
|
|
|
(5.10) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
2 p2 + p +7,5 |
|
|
p |
|
|
|
|
|
||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Установ вшееся |
|
|
|
е y(∞) в операторной форме при вход- |
|||||||||||||||||||||||||||
ном воздейств |
на с стему G(p) = 1/p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Y (∞) = 1 |
limW ( p) |
= |
5 |
|
= |
|
2 |
. |
|
|
|
|
(5.11) |
||||||||||||||
|
|
|
|
|
|
|
|
|
p p→0 |
|
|
|
|
|
|
|
7,5 p |
|
|
3p |
|
|
|
|
|
||||||
|
|
|
|
А |
|
|
|
|
|
||||||||||||||||||||||
Изображение Фурье для отклонения выходной величины e(t): |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
|
|
|
|
|
5 |
|
|
|
|
|
|
|||
|
E( jω) = y(∞) −W ( jω) |
|
= |
3 |
|
2(jω)2 |
|
+ jω+7,5 |
. |
|
(5.12) |
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
jω |
Д |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jω |
|
|
|
|
|
||||||
Интегральная квадратичная оценка через изображение Фурье: |
|||||||||||||||||||||||||||||||
|
1 |
∞ |
|
2 |
|
|
|
∞ |
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
2 |
|
|||
J2 = |
∫ |
|
E( jω) |
|
dω = |
1 ∫ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
jω |
dω; |
(5.13) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2π −∞ |
|
|
|
|
|
|
π 0 |
|
3 |
|
|
|
|
2 |
+ jω+7,5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2(jω) |
|
|
|
|
|
|||||||||||||||||
Для вычисления данного интеграла воспользуемсяИвозможностями программного комплекса Matlab. Функция quad выполняет интегрирование функций, используя квадратурную формулу Симпсона (адаптивный метод Симпсона) с заданной относительной погрешностью 1.0 E-6 [2, 6]. Функция quad('fun',a,b) возвращает численное значение определенного интеграла от заданной функции fun на отрезке [a b]. В случае формулы (5.13) верхний предел интегрирования ∞ необходимо заменить на очень большое число, допустим 1012.
>> J2=(1/pi)*quad('(abs((2/3-5./(2.*(j.*w).^2+j.*w+7.5))./(j.*w))).^2',0,10^12) J2 = 0.474074
Таким образом, интегральная квадратичная оценка J2 = 0, 474074.
28

Исходные данные для выполнения работы
Заданная структурная схема модели линейной системы управле-
|
ния представлена на рис. 5.2. |
|
|
|
|
|
|
||
|
Передаточные функции системы управления: |
|
|
||||||
С |
|
|
K2 |
; W3 ( p) = K3 . |
|||||
|
W1 ( p) = KП + K Д р; W2 ( p) = |
p(T 2 p +T p +1) |
|||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
В табл. 5.1 пр ведены численные значения параметров переда- |
||||||||
|
точных функци |
с стемы управления. |
|
|
|
|
|||
|
и |
|
|
|
|
|
Таблица 5.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ вар. |
KП |
KД |
K2 |
Т12 |
|
T2 |
K3 |
|
|
1 |
5 |
1 |
2 |
1 |
|
4 |
1 |
|
|
2 |
5 |
2 |
1 |
0,5 |
|
2 |
1,25 |
|
|
3 |
5 |
3 |
2 |
0,5 |
|
2 |
1 |
|
|
4 |
2,5 |
4 |
2 |
1 |
|
4 |
0,8 |
|
|
5 |
2,5 |
5 |
2 |
1,25 |
|
5 |
1 |
|
|
6 |
2,4 |
6 |
0,5 |
0,5 |
|
2 |
1,25 |
|
|
7 |
6 |
7 |
0,5 |
0,05 |
|
0,25 |
1 |
|
|
|
б |
|
|
|
|
|||
8 |
8 8 0,25 |
0,05 |
|
0,2 |
0,75 |
||||
|
9 |
4 |
9 |
0,25 |
0,025 |
|
0,1 |
1 |
|
|
|
|
А |
|
|
||||
10 |
9 |
10 0,33 0,05 |
0,2 |
1,5 |
|||||
1.Изобразить заданную структурнуюДсхему модели линейной системы управления и записать её передаточные функции.
2.По заданной структуре и передаточнымИфункциям системы управления получить передаточную функцию замкнутой системы.
3.Получить переходную характеристику системы при входном воздействии на систему G(p) = 1/p в операторной форме.
4.Вычислить установившееся значение выходной величины.
5.Записать изображение Фурье для отклонения выходной ве-
личины.
6.Записать выражение интегральной квадратичной оценки через изображение Фурье.
7.Вычислить с помощью программного комплекса Matlab значение интегральной квадратичной оценки.
29
|
|
Содержание отчета |
1. |
Название и цель работы. |
|
2. |
Передаточная функция замкнутой системы. |
|
3. |
Переходная характеристика системы y(t) при входном воз- |
|
С |
|
|
действии на систему G(p) = 1/p в операторной форме. |
||
4. |
Установившееся значение выходной величины. |
|
5. |
Изображение Фурье для отклонения выходной величины. |
|
6. |
Выражен е нтегральной квадратичной оценки через изо- |
|
бражен е Фурье. |
|
|
задания |
||
7. |
Функц я |
нтегрирования в Matlab. |
8. |
Значен е |
нтегральной квадратичной оценки. |
Вопросы |
для защиты лабораторной работы |
|||
1. |
Что представляют со ой интегральные оценки? |
|||
2. |
В чем недостаток линейной интегральной оценки, и в каких |
|||
случаях её допуст |
мо применять? |
|
||
3. |
Запишите выражение интегральной квадратичной оценки во |
|||
временной |
|
? |
|
|
4. |
|
области |
|
|
Запишите выражение переходной характеристики системы |
||||
при входном воздействии на систему G(p) = 1/p в операторной форме. |
||||
5. |
Запишите выражение изображения Фурье для отклонения |
|||
выходной величины. |
|
|||
6. |
|
|
А |
|
Запишите выражение интегральной квадратичной оценки че- |
||||
рез изображение Фурье. |
|
|||
7. |
В каких пределах интегрируется изображения Фурье для от- |
|||
клонения выходной величины? |
|
|||
8. |
Как реализуется вычислениеДопределенного интеграла в про- |
|||
граммном комплексе Matlab? |
И |
|||
|
|
|
|
|
30
Лабораторная работа № 6
Синтез линейной системы методом логарифмических амплитудных характеристик
С |
изучить синтез последовательных корректи- |
Цель работы − |
рующих звеньев линейных автоматических систем управления методом логар фм ческ х амплитудных характеристик.
Общие сведения
рудован е (промышленные ро оты, станки с числовым программным управлен ем, автомат зированные складские комплексы), содержат большое ч сло автоматических систем управления. К ним предъяв-
ляются высок е тре к качеству регулирования со стороны
ованияЭлектромехан ческие системы, включающие современное обо-
технолог ческого процесса. Поэтому вопросы анализа и синтеза сис-
тем управлен я для различных электромеханических объектов явля- |
|
ются актуальными. |
А |
Синтезбавтоматической системы управления – процесс нахож- |
|
дения математической модели и технической реализации управляющего или корректирующего устройства, обеспечивающего поддержание желаемых законов измененияДрегулируемой величины y(t) в соответствии с заданными показателями качества, режимам работы и т.д. при заданном объекте управления.
Для изменения динамического поведения системы в переходном режиме или повышения/обеспечения её устойчивости можно применять коррекцию динамических свойств в частотнойИобласти.
Одним из наиболее удобных и распространенных графоаналитических методов синтеза является метод логарифмических частотных характеристик (ЛАХ). Так как построение ЛАХ, как правило, может делаться почти без вычислительной работы в случае использования асимптотические ЛАХ [1, 3, 7, 8].
При использовании данного метода синтеза исходная система должна быть минимально-фазовой.
Минимально-фазовая система – система, у которой все корни pi
характеристического уравнения передаточной функции W(p) имеют отрицательные действительные части, т. е. расположены в левой комплексной полуплоскости (являются левыми).
31
У минимально фазовых систем существует однозначная зависимость между частотными характеристиками. То есть, располагая одной частотной характеристикой, можно построить остальные. Другими словами, в любой частотной характеристике заключена вся информация о поведении системы.
Рассмотрим синтез последовательного корректирующего звена
(КЗ) методом логарифмических частотных характеристик. В кото-
ром при построенной ЛАХ нескорректированной системы LН(ω) и сформ рованной желаемой ЛАХ LС(ω), определяются ЛАХ LКЗ(ω),
параметры |
схема реал зации последовательного КЗ [1, 3, 7, 8]. |
|
|
|
нтез КЗ преследует две следующие цели: |
|
|
С |
|
||
1. |
определен е ЛАХ КЗ LКЗ(ω); |
|
|
2. |
определен е передаточной функции КЗ WКЗ(p) и её параметров. |
||
Процесс с нтеза корректирующего звена линейной системы ме- |
|||
тодом логар фм ческ х амплитудных характеристик включает в себя |
|||
следующ е |
[1, 3, 7, 8]: |
|
|
шаги |
|
||
1. |
Построен е сходной Л Х. Под исходной ЛАХ понимается |
||
частотная характер ст ка нескорректированной разомкнутой систе- |
|||
мы управления LН(ω), состоящей из объекта управления, управляю- |
|||
щего устройстваби регулятора ез КЗ. |
|
||
2. |
Построение желаемой Л Х. Построение желаемой ЛАХ |
||
LС(ω) делается на основе тех требований, которые предъявляются к |
|||
проектируемой системе управления. |
|
||
3. |
Определение характеристики корректирующего звена. Пу- |
||
|
|
А |
|
тем графического вычитания частотных характеристик получаем |
|||
ЛАХ КЗ |
|
|
|
|
|
LКЗ(ω) = LC (ω) − LН (ω) . |
(6.1) |
Д Таким образом, при использовании ЛАХИвесьма легко осущест-
вляется синтез последовательных КЗ, так как их ЛАХ получается простым вычитанием ординат исходной ЛАХ из ординат желаемой.
4.Техническая реализация корректирующих средств. По виду ЛАХ, коэффициенту усиления и требуемым частотам сопряжения и среза необходимо подобрать тип, передаточную функцию и параметры КЗ последовательного типа.
5.Проверочный расчёт и построение переходного процесса. В
случае необходимости полученная система управления вместе с корректирующим звеном может быть исследована обычными методами анализа устойчивости и качества управления.
32
Под желаемой понимается такая ЛАХ разомкнутой системы, которая обеспечивает заданные показатели качества регулирования системы в замкнутом состоянии. Желаемую ЛАХ LС(ω) следует построить в виде кусочно-линейного графика, т.е. в виде сопряженных
асимптот, соединяющих участки ЛАХ. Желаемая ЛАХ LС(ω) может быть разбита на три характерных участка: низкочастотный НЧ, сред-
СЧ
нечастотный и высокочастотный ВЧ.
Рекомендуется желаемую ЛАХ LС(ω) максимально приблизить к исходной ЛАХ нескорректированной системы управления LН(ω) для упрощен я т па КЗ.
НЧ участок определяет точность системы в установившемся ре-
жимепоэтому НЧ ас мптота желаемой ЛАХ должна совпадать с НЧ асимптотой ЛАХ нескорректированной системы, если коэффициент усилен я нескоррект рованной системы обеспечивает требуемую точность в стат ческом (для статических систем) или динамическом (для астат ческ х с стем) режимах.. Для статических систем НЧ участок меет в д гор зонтальной линии и отстоит от оси абсцисс на
20lgKРАЗ, где KРАЗ – коэффициент передачи разомкнутой системы. Для |
|
астатических систем первого порядка НЧ участок имеет наклон −20 |
|
дБ/дек с |
перес чением точки (L = 20lgKРАЗ; lgω = 0). |
|
обязательным |
СЧ участок желаемой Л ЧХ определяет качество переходного |
|
процесса и запасы устойчивости системы и строится на основе задан- |
|
ных показателей качества переходного процесса: времени регулиро- |
|
вания tР и величины максимального перерегулирования σ. СЧ участок |
|
РАЗ |
|
располагается по обе стороны от точки пересечения желаемой ЛАХ |
|
Д |
|
LС(ω) оси абсцисс. Точка пересечения соответствует частоте среза ωC. |
|
Среднечастотный участок должен обязательно иметь наклон –20 |
|
дБ/дек и продолжаться от ωC до ординат L1 |
и L2, где LС = (0 – L2) – |
желаемый запас устойчивости по амплитуде. |
И |
|
|
ВЧ участок желаемой ЛАЧХ не оказывает существенного влия- |
|
ния на динамические свойства системы на рабочей частоте. Поэтому |
|
для упрощения КЗ рекомендуется выбирать сопрягающие частоты по |
|
возможности такие же, как в характеристике неизменяемой части сис- |
|
темы LН(ω), а наклон ВЧ асимптоты такой же и или меньший на 20 дБ/дек, чем у ЛАХ нескорректированной системы на этом участке.
СЧ сопрягается с соседними либо непосредственно путем продолжения СЧ участка за счет его расширения и, соответственно, увеличения запасов устойчивости L1 и L2, либо с помощью сопрягающих прямых, имеющих наклон –40 дБ/дек, что конечно, усложнит ЛАХ и реализацию КЗ.
33
Для восстановления передаточной функции минимальнофазового КЗ по полученной ЛАХ LКЗ(ω) используются следующие правила [1, 3, 7, 8]:
1. Находится коэффициент усиления KКЗ, исходя из требуемой точности системы управления в статическом (для статических систем) или динамическом (для астатических систем) режимах.
2. Для точек излома (перегиба) ЛАХ LКЗ(ω) определяются соответствующие им частоты перегиба ω0iкз и вычисляются постоянные
времени передаточной функции КЗ |
|
||||
С Tiкз = |
1 |
[с]. |
(6.2) |
||
ω0iкз |
|||||
3. |
наклоны смежных отрезков в точке перегиба отличаются |
||||
на +20 дБ/дек ( злом вверх), то в числитель передаточной функции |
|||||
КЗ помещается множ тель (Tip +1). Если же наблюдается отличие на |
|||||
–20 дБ/дек ( |
злом вн з), то множитель (Tip +1) помещается в знаме- |
||||
Если |
|
|
|
||
натель передаточной функции КЗ. |
|
||||
4. При разности наклонов в точке перегиба, равной ±40 дБ/дек |
|||||
(излом вверх/вниз) в числитель/знаменатель передаточной функции |
|||||
помещаетсябфорсирующие и апериодические звенья второго порядка |
|||||
(T1i2p +T2ip +1). |
|
|
|
|
|
После построения желаемой характеристики LС(ω) и определе- |
|||||
ния параметров КЗ необходимо построить частотные характеристики |
|||||
и определить запасы устойчивости L и Δφ, которые должны удовле- |
|||||
|
|
А |
|
||
творять требованиям, предъявляемым к системе управления. |
|
||||
|
|
Д |
|
||
К схеме реализации КЗ предъявляется три основных требования: физическая реализуемость, условие грубости (или нечувствительности к малым изменениям параметров) и простотаИреализации.
Схема реализации КЗ выполняется из типовых схем. Если коэффициент усиления КЗ KКЗ ≤ 1 , то в качестве корректирующего устройства рекомендуется применять типовые пассивные четырёхполюсники, состоящие из RLC -цепей. Если корректирующее устройство не удается реализовать одним звеном, то соединяют последовательно несколько звеньев, как правило, через разделительные усилители. При этом ЛАХ отдельных звеньев суммируются.
В случае KКЗ > 1 рекомендуется использовать активное устройство на базе операционного усилителя.
Схемы типовых корректирующих звеньев электромеханических систем приведены в прил. 1.
34
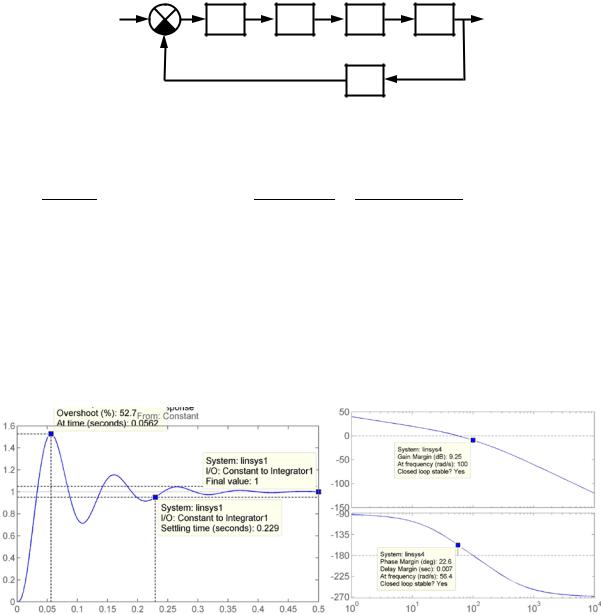
|
|
Пример. Пусть дана исходная линейная астатическая система |
||||||||||||||||
управления (рис. 6.1). Необходимо синтезировать КЗ WКЗ. |
|
|
||||||||||||||||
|
|
|
|
g |
|
WКЗ |
|
W1 |
|
|
W2 |
W3 |
y |
|
|
|||
|
|
|
|
+ |
–y |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W4 |
|
|
|
|
|
|
|
|
Р с. 6.1. Структурная схема модели линейной системы управления |
|
|||||||||||||||
|
|
Передаточные |
|
|
системы управления: W1 = K1 = 5; |
|
||||||||||||
СK 40 |
|
; W = |
|
K |
3 |
|
= |
|
0,5 |
|
; |
W = K |
|
=1. |
||||
W |
= |
2 |
= |
0,004 p +1 |
|
|
+1) |
p(0,025 p |
+1) |
|
||||||||
2 |
|
T p +1 |
|
3 |
|
p(T p |
|
|
4 |
4 |
|
|||||||
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Переходная временная характеристика замкнутой системы и |
||||||||||||||||
частотные характер ст ки разомкнутой системы управления пред- |
||||||||||||||||||
ставлены на р с. 6.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
функции |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Исходная с стема не удовлетворяет требованиям по перерегули- |
||||||||||||||||
рованию σ, так как наклон исходной ЛАХ на частоте среза слишком |
||||||||||||||||||
велик. Кроме того, запасы устойчивости по амплитуде |
Lн = 9,25 дБ и |
|||||||||||||||||
по фазе Δφнб= 22,6° меньше тре уемых L ≥ 10 дБ и Δφ ≥ 30°. |
|
|
||||||||||||||||
|
|
|
|
|
А |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Д |
|
|||||||||
|
|
|
|
а |
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
Рис. 6.2. Характеристики системы управления: |
|
|
|
|||||||||||
|
|
а – переходная временная; б – логарифмические частотные |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||
|
|
Построение исходной ЛАХ. На начальном участке исходной |
||||||||||||||||
ЛАХ (рис. 6.3) имеет наклон –20 дБ/дек, что соответствует интегри- |
||||||||||||||||||
рующей составляющей. Далее наклон асимптот ЛАХ будет увеличи- |
||||||||||||||||||
ваться на –20 дБ/дек после каждой частоты сопряжения системы, обу- |
||||||||||||||||||
славливаемыми постоянными времени звеньев системы. |
|
|
||||||||||||||||
35
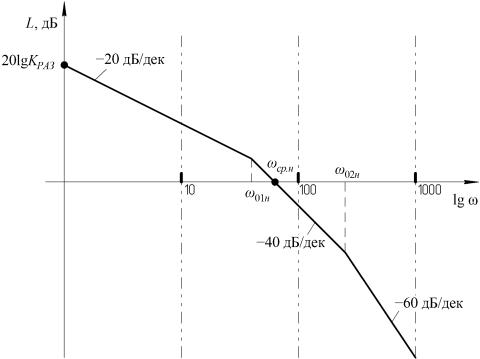
Коэффициент передачи разомкнутой системы KРАЗ = 100.
LРАЗ = 20lgKРАЗ = 40.
С |
|
||||||
и |
|||||||
|
1 |
|
|
1ЛАХ |
|||
|
бРис. 6.3. исходной системы управления |
||||||
Частоты сопряжения: |
|||||||
ω |
= |
1 |
= |
1 |
= 40 рад/с. lgω01н = 1,6 дек. |
||
|
|
0,025 |
|||||
01н |
T |
|
|
|
|||
|
3 |
|
|
|
|
||
ω02н = |
|
|
= |
0,004 = 250 рад/с. lgω02н = 2,4 дек. |
|||
T |
|
||||||
|
2 |
|
|
|
|
||
Построение желаемой Л Х. |
|||||||
|
|
|
|
|
|
|
И |
Низкочастотный участок.Д
На данном участке, отвечающем за отработку медленно меняющихся сигналов, синтезируются точностные свойства системы в статическом (для статических систем) или динамическом (для астатических систем) режимах.
Так как исходная система астатична, то точность в установившемся режиме при единичной обратной связи будет соответствует требуемой, так как статизм системы δg, определяемый передаточной функцией статического режима замкнутой системы W(0) равен 1.
Требования к динамической точности также не сформулированы, поэтому НЧ асимптота желаемой ЛАХ должна совпадать с НЧ асимптотой ЛАХ нескорректированной системы (рис. 6.4).
36
Среднечастотный участок.
В первом приближении время регулирования tP систем может быть оценено по величине частоты среза желаемой ЛАХ разомкнутой
системы ωср.с:
С |
|
2πn |
|
|
|
tP ≈ ω . |
(6.3) |
||||
|
|
|
ср.с |
|
|
где n – ч сло выбросов переходной характеристики за установившее- |
|||||
ся значен |
е регул |
руемой величины в течении переходного процесса. |
|||
логарифмческом масшта е равно lgωср.с = lg31,6 = 1,5 дек (см. рис. 6.4). |
|||||
Отсюда можно примерно определить частоту среза желаемой |
|||||
ЛАХ можно определ ть исходя из допустимого времени регулирования |
|||||
системы, |
сходя |
з апериодического или колебательного характера пе- |
|||
ется, то пр мем частоту среза желаемой ЛАХ ωср.с = 31,6 рад/с., что в
реходной характер ст ки. Посколькублогран чений на время регулирования tP не накладыва-
Тогда пр |
женное время регулирования tP составит в случае |
||||||
|
|
2π 1 |
|
|
2 3,1416 |
|
|
одного выброса: tP ≈ ω |
|
≈ |
31,6 |
≈ 0,2 с, |
|||
|
|
ср.с |
|
|
|
|
|
двух выбросов: tP ≈ |
2π 2 |
≈ |
4 3,1416 |
≈ 0,4 с и т.д. |
|||
ω |
|
31,6 |
|||||
|
|
ср.с |
|
|
|
Д |
|
Наклон СЧ участкаАдолжен обязательно иметь –20 дБ/дек, для отсутствия перерегулирования в системе управления (см. рис. 6.4).
Ширину СЧ участка выбираем слева – из соображений удобства сопряжения с НЧ участком до lgω02с = 1 дек, а справа – до частоты со-
пряжения исходной ЛАХ lgω03с = lgω01н = 1,6 дек (см. рис. 6.4). |
|
Высокочастотный участок. |
И |
|
|
Для упрощения КЗ выбираем наклон ВЧ асимптоты желаемой ЛАХ после частоты сопряжения lgω03с меньшим на 20 дБ/дек, чем у ЛАХ нескорректированной системы LН(ω) на этом участке (см. рис. 6.4).
СЧ сопрягается с ВЧ участком непосредственно за счёт его расширения до частоты сопряжения lgω03с, а с НЧ участком с помощью сопрягающей прямой, имеющей наклон –40 дБ/дек от частоты сопряжения lgω01с = 0,5 дек до частоты сопряжения lgω02с = 1 дек (см. рис. 6.4).
Определение характеристики корректирующего звена. Путем графического вычитания частотных характеристик получаем ЛАХ КЗ
(см. рис. 6.4).
37
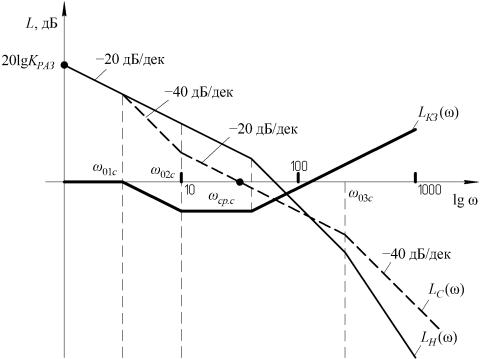
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и |
|
|
|
||||||||||||||||
|
Р с. 6.4. Желаемая Л Х системы управления с ЛАХ КЗ |
|
|||||||||||||||||
По вышеописанным правилам и полученной ЛАХ LКЗ(ω) восста- |
|||||||||||||||||||
навливаем передаточнуюбфункцию минимально-фазового КЗ: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
W |
КЗ |
= |
(T2кз p +1)(T3кз p +1) . |
(6.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T1кз p + |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
Вычисляются постоянныеАвремени передаточной функции КЗ по |
|||||||||||||||||||
соответствующим им частотам сопряжения ЛАХ LКЗ(ω). |
|
||||||||||||||||||
T |
= |
1 |
= |
|
1 |
|
|
|
|
≈ |
0,316 с. |
И |
|||||||
ω01кз |
100,5 |
|
|
||||||||||||||||
1кз |
|
|
|
|
|
|
|
|
|
|
|||||||||
T2кз = |
1 |
|
= |
1 |
|
= 0,1 с. |
|
||||||||||||
|
|
|
|
|
|||||||||||||||
|
ω02кз |
|
|
101 |
|
|
|
|
|||||||||||
T |
= |
|
1 |
|
= |
|
1 |
|
|
|
|
≈ |
0,025 с. |
|
|
||||
|
ω03кз |
|
101,6 |
|
|
|
|
||||||||||||
3кз |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
WКЗ = |
|
(0,1p +1)(0,025 p +1) |
. |
|
|
||||||||||||||
|
(0,316 p +1) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
После определения параметров и передаточной функции КЗ необходимо построить частотные характеристики скорректированной системы и проверить запасы устойчивости L и Δφ, которые должны удовлетворять требованиям к системе управления (рис. 6.5).
38
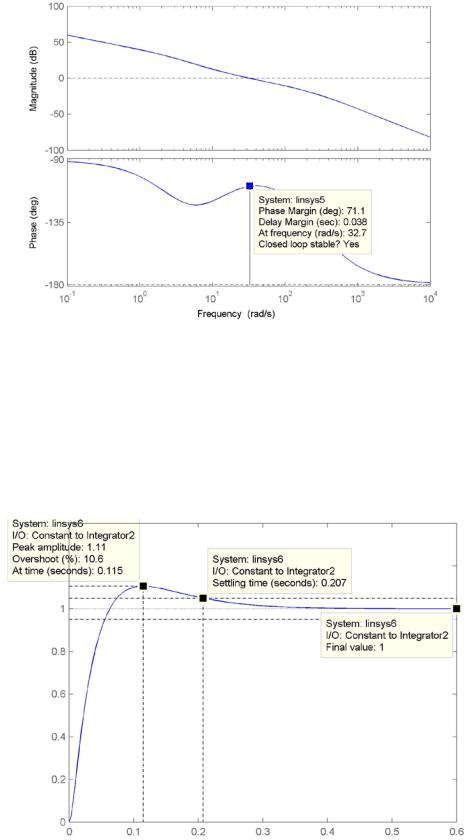
СРис
. 6.5. Логарбфм ческие частотные характеристики скорректированной
системы управления
Как видно из графиковА, что запасы устойчивости по амплитуде LС = ∞ дБ и по фазе ΔφС = 71,1°, что более чем удовлетворительно.
Переходная временная характеристика скорректированной системы управления представлена на рис. 6.6.
Д И
Рис. 6.6. Переходная временная характеристика скорректированной
системы управления
39
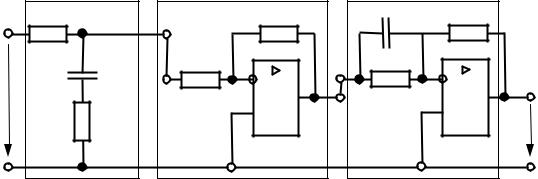
Схема реализации КЗ выполняется из типовых схем пассивных |
||||||||||||
четырёхполюсников, состоящих из RLC-цепей. |
|
|
|
|||||||||
В ряде случаев требуемая ЛАХ и соответствующая передаточная |
||||||||||||
функция КЗ не могут быть реализованы одной элементарной схемой че- |
||||||||||||
тырёхполюсника. В этом случае используют последовательное соеди- |
||||||||||||
нение нескольких корректирующих каскадов. |
|
|
|
|
||||||||
В нашем случае, согласно табл. П.1, выберем последовательное |
||||||||||||
соединение пассивного П и активного А КЗ, соединенных раздели- |
||||||||||||
тельным |
нверт рующ м повторителем напряжения ПН (рис. 6.7). |
|||||||||||
|
R1 |
П ПН |
|
Rоc |
А |
C2 |
R4 |
|
||||
С |
|
Rвх |
|
|
|
|
|
|
|
|
||
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
Uвх |
|
|
|
|
|
|
|
|
|
R3 |
|
|
иR2 |
|
|
|
|
|
|
Uвых |
|||||
|
|
бРис. 6.7. Схема реализации КЗ системы управления |
|
|
||||||||
На НЧ и СЧ участках |
удет действовать пассивное КЗ П с пере- |
|||||||||||
даточной функцией: |
|
|
(T2 |
кз p +1) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(6.5) |
|||
|
|
|
|
АW = |
|
|||||||
|
|
|
|
|
П |
(T |
|
p +1) |
|
|
|
|
|
|
|
|
|
|
1кз |
|
|
|
|
|
|
с постоянными времени: T1кз |
= (R1 + R2 )C1; T2кз |
= R2C1. |
|
|
||||||||
Разделительный инвертирующий повторитель напряжения ПН: |
||||||||||||
|
|
|
|
WПН = −1 |
Дпри Rвх = Rоc; |
(6.6) |
||||||
На СЧ и ВЧ участках будет действовать активное КЗ А с переда- |
||||||||||||
точной функцией: |
|
WА = −K(T3кз p +1); |
|
|
|
(6.7) |
||||||
|
|
|
|
|
|
|
||||||
с параметрами: T3кз |
|
|
|
|
|
|
И |
|||||
= R3C2 ; K = R4/ R3 = 1 при R3 = R4. |
|
|
||||||||||
Для практического исполнения корректирующей цепи выбираем |
||||||||||||
следующие стандартные номинальные значения RC параметров из |
||||||||||||
ряда E48 (прил. 2): R1 = 40,2 кОм; R2 = 18,7 кОм; R3 = R4 = 7,50 кОм; |
||||||||||||
С1 = 5,36 мкФ; С2 = 3,32 мкФ. Данные параметры с достаточной сте- |
||||||||||||
пенью точности обеспечивают требуемые постоянные времени КЗ. |
||||||||||||
40
Исходные данные для выполнения работы
Заданная структурная схема модели линейной системы управле-
ния представлена на рис. 6.1. |
|
|
|
|
|
||||||
Передаточные функции системы управления: |
|
|
|||||||||
С |
|
|
20 |
|
; W3 |
|
|
K3 |
|
; W4 =1. |
|
W1 |
= 2; W2 = |
|
0,004 p +1 |
= |
p(0,025 p +1)(0,1p |
+1) |
|||||
Необход мо с нтезировать КЗ WКЗ |
линейной системы методом |
||||||||||
логарифм ческ х ампл тудных характеристик. |
|
|
|||||||||
систем |
|
|
|
|
|
||||||
|
|
|
Порядок выполнения работы |
|
|
||||||
1. |
|
ть заданную структурную схему модели линейной |
|||||||||
|
Изобраз |
|
|
|
|||||||
ы управлен я |
записать её передаточные функции. |
||||||||||
2. |
Получ ть с помощью инструмента Linear Analysis в Simulink |
||||||||||
переходную временную характеристику замкнутой исходной системы и |
|||||||||||
частотные характер ст ки разомкнутой исходной системы управления. |
|||||||||||
3. |
|
|
|
А |
|
|
|||||
Провести анализ качества регулирования и устойчивости ис- |
|||||||||||
ходной системы по полученным характеристикам. |
|
|
|||||||||
4. |
Произвести построение исходной асимптотической ЛАХ, |
||||||||||
определив частоты сопряжения и наклоны асимптот. |
|
|
|||||||||
5. |
|
|
|
|
|
|
Д |
||||
Произвести построение желаемой асимптотической ЛАХ, |
|||||||||||
придерживаясь вышеописанных правил. |
|
|
|
||||||||
6. |
Путем графического вычитания частотных характеристик |
||||||||||
получить характеристику корректирующего звена. |
|
|
|||||||||
7. |
По вышеописанным правилам и полученной ЛАХ КЗ восста- |
||||||||||
|
|
|
|
|
|
|
|
|
И |
||
новить передаточную функцию корректирующего звена и вычислить |
|||||||||||
его параметры по частотам сопряжения. |
|
|
|
||||||||
8. |
Получить с помощью инструмента Linear Analysis в Simulink |
||||||||||
переходную временную характеристику замкнутой скорректированной |
|||||||||||
системы и частотные характеристики разомкнутой скорректированной |
|||||||||||
системы управления. |
|
|
|
|
|
|
|
|
|||
9. |
Провести анализ качества регулирования и устойчивости |
||||||||||
скорректированной системы управления по полученным характери- |
|||||||||||
стикам. |
|
|
|
|
|
|
|
|
|
|
|
10. |
Спроектировать схемную реализацию корректирующего зве- |
||||||||||
на и подобрать параметры корректирующей цепи из стандартных рядов RC параметров.
41
|
|
Содержание отчета |
1. |
Название и цель работы. |
|
2. |
труктурная схема модели и передаточные функции линей- |
|
ной системы управления. |
||
С |
|
|
3. |
Характеристики исходной системы в Simulink. |
|
4. |
Показатели качества регулирования и запасы устойчивости |
|
исходной системы. |
|
|
5. |
Ас мптот ческ е ЛАХ, полученные в процессе синтеза. |
|
6. |
Передаточная функция и параметры корректирующего звена. |
|
Показатели |
||
7. |
Характер ст ки скорректированной системы в Simulink. |
|
8. |
|
качества регулирования и запасы устойчивости |
скоррект рованной с стемы. |
||
9. |
хемная реал зация корректирующего звена и параметры |
|
|
б |
|
коррект рующей цепи.
Вопросы задания для защиты лабораторной работы
1.Что такое синтез автоматической системы управления?
2.Что такое минимально-фазовая система и в чем её особенность в плане характеристик?
3.В чем суть метода логарифмических частотных характери-
стик?
4.Каковы цели синтеза корректирующего звена?
5.Перечислите основные этапы синтеза корректирующего звена.
6.Как получить характеристику корректирующего звена?
7.Какие рекомендации имеются при построении желаемой асимптотической ЛАХ?
8.Как происходит сопряжение участков желаемой асимптотической ЛАХ?
9.Как восстановить передаточную функцию корректирующего звена по полученной ЛАХ?
10.Как производится схемная реализация корректирующего звена и подбор параметров корректирующей цепи?АИ
42
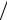
Лабораторная работа № 7
Синтез линейного автоматического ПИ-регулятора для статической линейной системы
СНа более простой корневой метод разработан Т. Н. Соколовым. ущность его свод тся к следующему. С точки зрения скорейшего затухан я переходного процесса важно, чтобы вещественные части
Цель работы − изучить корневой метод синтеза ПИ-закона ре-
гулирования для линейных статических систем управления.
Общие сведения
шимикачества – степень устойчивости [3, 4, 8].
всех корней характер стического уравнения системы были наиболь- , т.е. с стема мела максимально большой корневой показатель
Задача с нтеза с стем управления по корневым показателям качества став тся следующим о разом. Задана структура системы управления и тре уется определить вектор параметров регулятора {k}
из условия [3, 4, 8] |
|
|
|
|
|
|
|
|
б |
|
|
||||||
|
* |
= η({k |
* |
}); |
|
|
||
|
η |
|
. |
(7.1) |
||||
|
|
|
* |
|
|
′ |
||
|
|
|
|
|
|
|
||
|
µ({k |
|
})≤ µ . |
|
|
|||
Здесь η* называется оптимальной степенью устойчивости и {k*} |
||||||||
|
А |
|
||||||
– оптимальным вектором параметров регулятора, μ' – допустимая ко- |
||||||||
|
|
Д |
|
|||||
лебательность системы. Порядок полинома регулятора не должен превышать п – 1 (п – степень характеристического уравнения системы).
Длительность отдельных составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части Re(pi) определяющих их корней характеристического уравнения системы. Колебательность системы оценивается отношением веществен-
ных и мнимых частей корней характеристического уравнения системы. Длительность переходного процесса определяется по корневому
показателю степени устойчивости: |
И |
|
tP ≈3 η. |
||
(7.2) |
Между колебательностью переходной характеристики μ и корневым показателем степенью колебательности m существует связь
µ ≈ e |
− |
2π |
(7.3) |
|
m . |
43
Рассмотрим характеристическое уравнение системы управления
3-го порядка с коэффициентами ai > 0, i = 0, 1, 2, 3: |
|
||||||||||||||||||||||
A(p) = a0p3 |
|
+ a1p2 + a2p + a3 = 0. |
(7.4) |
||||||||||||||||||||
Такое характеристическое уравнение будет иметь три корня вида |
|||||||||||||||||||||||
С |
|
|
|
|
pi = αi ± jβi. |
|
|
|
|
|
(7.5) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
умма абсолютных значений вещественных частей всех корней |
|||||||||||||||||||||||
численно равна первому коэффициенту приведенного характеристи- |
|||||||||||||||||||||||
ческого уравнен я (7.4) [3, 4]: |
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
||||||||
стического |
|
|
|
|
|
|
|
|
|
|
. |
|
(7.6) |
||||||||||
|
|
|
α |
+ |
α |
2 |
|
+ |
α |
3 |
|
= |
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|||||
Как звестно степень устойчивости η и определяется минималь- |
|||||||||||||||||||||||
ным абсолютным значением вещественной части корней характери- |
|||||||||||||||||||||||
уравнен я (см. ф. (4.4)). |
|
|
|
|
|
|
|
|
|
||||||||||||||
б |
|
|
|
|
|
|
|||||||||||||||||
Поэтому при заданной величине этого коэффициента максималь- |
|||||||||||||||||||||||
но возможная степень устойчивости ηmax |
|
устойчивого полинома А(q) |
|||||||||||||||||||||
получаются при равенстве вещественных частей всех корней [3, 4] |
|
||||||||||||||||||||||
А |
|
||||||||||||||||||||||
|
α |
= |
α |
2 |
|
= |
α |
3 |
|
= η |
max |
= |
1 |
a1 |
(7.7) |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 a0 |
|
|||||
Из общего числа корней характеристического уравнения третьего порядка всегда можно выделить один корень, который является действительными и характеризует быстро затухающие составляющие, оказывающие влияние только на начальной стадии переходного процесса. И два сопряженных корня, которые и определяют ход основно-
Поэтому характеристическоеДуравнение системы управления (7.4) можно преобразовать, выделив из него множитель, дающий при
го процесса [3, 4, 8].
решении действительный отрицательный корень p3 = –α3, с макси-
мальной степенью устойчивости ηmax [3, 4, 8]: |
|
A(p) = (p + ηmax)(q0p2 + q1p + q2) = 0. |
(7.8) |
Для того чтобы вещественные части корней второго сомножи- |
|
теля (7.8) были равны |α1| = |α2| = ηmax необходимоИ, чтобы: |
|
a0 = q0; |
(7.9) |
a1 = q0ηmax + q1 = a0ηmax + q1; |
(7.10) |
a2 = q1ηmax + q2; |
(7.11) |
a3 = q2ηmax. |
(7.12) |
44

Откуда определяются коэффициенты полинома (7.8) [3, 4, 8]:
q1 = a1 – a0ηmax; |
(7.13) |
q2 = a2 – q1ηmax = a3/ηmax. |
(7.14) |
Необходимым условием устойчивости, |
согласно критерию |
А. тодолы, является положительные значения коэффициентов qi: |
|
(qi > 0, i = 0, 1, 2). |
(7.15) |
Второй сомнож тель (7.8) будет определять основной характер |
||||||||||||||||||||||||||||||||||||||
переходного процесса. Для уменьшения погрешностей проектируе- |
||||||||||||||||||||||||||||||||||||||
дит1 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
1 |
|
|
|
|
||||||||
мой с стемы важно, |
чтобы коэффициент q2 |
в сомножителе имел как |
||||||||||||||||||||||||||||||||||||
Сможно большую вел ч ну. Однако чрезмерное увеличение q2 |
приво- |
|||||||||||||||||||||||||||||||||||||
к колебательному характеру переходного процесса. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Корни второго сомножителя являются сопряженными α1 = α2, |
||||||||||||||||||||||||||||||||||||||
|β1| = |β2| |
(7.8) определяются выражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
q |
|
|
|
q2 |
|
|
|
q |
|
|
|
|
|
|
|
|
|
q |
|
|
|
q |
|
|
|
q2 |
|
|
|
||||
p1,2 = α1 ± jβ1 = −2q ± |
|
|
|
|
|
|
− |
|
|
|
|
|
|
= − |
|
± j |
|
|
|
|
|
− |
|
. |
|
(7.16) |
||||||||||||
|
|
|
4q2 |
|
q |
|
|
|
|
|
2q |
|
|
q |
|
|
4q2 |
|
||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|||
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Из выражения (7.3) можно получить ограничение по колеба- |
||||||||||||||||||||||||||||||||||||||
тельности, бсвязывающее отношение вещественной α1 |
и мнимой β1 |
|||||||||||||||||||||||||||||||||||||
частей корней второго сомножителя (7.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
m |
≤ lnµ′ |
|
или |
−2π |
|
|
1 |
|
|
≤ lnµ′. |
|
|
|
|
|
|
|
|
|
|
(7.17) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
Д′ |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как вещественные части корней второго сомножителя (7.8) |
||||||||||||||||||||||||||||||||||||||
|α1| = ηmax, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||
|
|
|
|
|
|
|
β |
|
≤ 2πηmax . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.18) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−lnµ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из уравнений (7.16) и ( 7.18) получим ограничение для коэффи- |
||||||||||||||||||||||||||||||||||||||
циента q2 |
по допустимой колебательности системы: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2πηmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
q2 −η2max |
≤ |
; |
|
|
|
|
|
|
|
|
|
|
|
(7.19) |
||||||||||||||||||
|
|
|
|
|
|
q0 |
|
|
|
|
|
|
|
|
−lnµ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
− q |
|
2πη |
2 |
+ q η2 |
|
|
|
≤ q |
≤ q |
2πη |
2 |
+ q η2 . |
|
(7.20) |
|||||||||||||||||||||||
|
|
max |
|
|
|
|
|
max |
|
|||||||||||||||||||||||||||||
|
0 |
|
−ln µ′ |
|
|
0 max |
|
|
2 |
|
|
0 |
−ln µ′ |
|
|
|
0 |
max |
|
|
||||||||||||||||||
Данное ограничение для коэффициента q2 должно соблюдаться совместно с условием устойчивости (7.15).
45
Пример. Передаточная функция исходной разомкнутой системы управления имеет вид
|
|
WРАЗ ( p) = |
|
|
|
|
|
|
|
0,5 |
|
|
|
|
. |
|
|
|
(7.21) |
||||||||
|
|
|
0,025 p2 +0,05 p +1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Требуется синтезировать корневым методом параметры после- |
|||||||||||||||||||||||||||
довательного ПИ-регулятора (корректирующего звена): |
|
|
|
||||||||||||||||||||||||
|
WПИ ( p) = KП + |
KИ |
= |
|
1 |
(KП р+ KИ ). |
|
|
|
(7.22) |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
р |
|
|
|
|
|
|
|
|
|
|
||
При допуст мой колебательности системы μ' = 75%. |
|
|
|
||||||||||||||||||||||||
Передаточная |
я замкнутой системы WЗАМ(p) с ПИ-звеном: |
||||||||||||||||||||||||||
С |
WЗАМ ( p) = |
|
|
|
WРАЗ ( p)WПИ |
( p) |
= |
|
|
|
|
|
|||||||||||||||
|
|
1+WРАЗ ( p)WПИ ( p) |
. |
|
(7.23) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
0,5(KП р+ KИ ) |
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
+(1+ |
0,5KП )р+0,5KИ |
|
|
|
||||||||||||||
функци0,025 p +0,05 p |
|
|
|
|
|||||||||||||||||||||||
Характер ст ческое уравнение системы с ПИ-регулятором: |
|
||||||||||||||||||||||||||
A(p)= 0,025 p3 +0,05 p2 +(1+0,5KП )р+0,5KИ . |
|
(7.24) |
|||||||||||||||||||||||||
|
|
a0 |
|
|
a1 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
||||
б |
2 |
|
|
|
|
3 |
|
|
|
||||||||||||||||||
Система управления |
удет устойчива при: |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
KП > −2; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
K |
И |
> 0. . |
|
|
|
|
|
|
|
|
(7.25) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
А |
|
|
|
|
|
||||||||||||||||||||
Максимально возможная степень устойчивости ηmax из (7.7) |
|
|
|
||||||||||||||||||||||||
|
|
ηmax = |
1 |
a1 |
|
|
= |
1 |
0,05 |
= |
2 |
= 0,666. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||
|
|
|
3 a0 |
|
|
|
|
3 0,025 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Д |
|
- |
|||||||||||||||
Выделим из характеристического |
уравнения системы |
с |
|||||||||||||||||||||||||
|
|
|
|
q0 = a0 = 0,025; |
ПИ |
||||||||||||||||||||||
регулятором множитель, дающий при решении действительный отрицательный корень с максимальной степенью устойчивости p3 = – ηmax:
A(p) = (p + 2/3)(q0p2 + q1p + q2) = 0.
q1 = a1 – a0ηmax = 0,0333;
Коэффициент q2, рассчитываемый по формуле (7.14) содержит неизвестные параметры ПИ-регулятора, поэтому формула (7.14) дает уравнение, связывающее параметры ПИ-регулятора, при которых достигается максимальная степень устойчивости ηmax:
46
q2 = a2 – q1ηmax = a3/ηmax = (1+0,5KП )−0,0222 = 23 0,5KИ . (7.26)
Ограничение для коэффициента q2 по допустимой колебательности системы:
С |
|
2π 0,666 2 |
|
2 |
|
||
q2 |
≤ 0,025 |
|
|
+0,025 0,666 |
|
=5,3. |
|
|
|
|
−ln(0,75) |
|
|
|
|
q2 |
|
2π 0,666 2 |
|
2 |
|
|
≥ −0,025 |
|
|
+0,025 0,666 |
|
= −5,27. |
|
|
|
|||||
нижниеП |
|
|
П |
|||
|
|
−ln(0,75) |
|
|
|
|
Здесь важными являются верхние пределы ограничения, так как пределы параметров диктуются условиями устойчивости
(7.15). огласно зав с мости (7.26) и условию устойчивости (7.15) по- |
|
б |
|
лучим огран чен я по параметрам ПИ-регулятора |
|
0 < (1 +0,5K )−0,0222 ≤ 5,3 или −2 < K ≤ 8,64. |
(7.27) |
0 < 3 KИ ≤ 5,3 или 0 < KИ ≤ 7,06 . |
(7.28) |
ЗАМ |
|
4 |
|
Введение в структуру системы управления ПИ-закона регулирования приводит к появлению полинома, находящегося в числителе
передаточной функции замкнутой системы W |
(p): |
B(p)= 0,5KП р+0,5KИ . |
(7.29) |
Такой полином обеспечивает дополнительные вынужденные колебания в системе. Данный факт при синтезе параметров ПИрегулятора обуславливает появление дополнительного условия по
корню полинома числителя (нулю): |
|
И |
||
|
|
|
||
|
рД≤ 0. |
(7.30) |
||
|
z |
|
|
|
что обеспечивается при |
KП |
≥ 0; |
|
(7.31) |
|
> 0. |
|
||
|
KИ |
|
|
|
Тогда с учетом полученных уравнений и ограничений, связывающих параметры ПИ-регулятора, можно выделить следующие условия оптимальных параметров ПИ-регулятора:
0,5KП +0,9778 = 0,75KИ ; |
|
|
(7.32) |
0 ≤ KП ≤8,64; |
|
|
|
0 < KИ ≤ 7,06. |
|
47
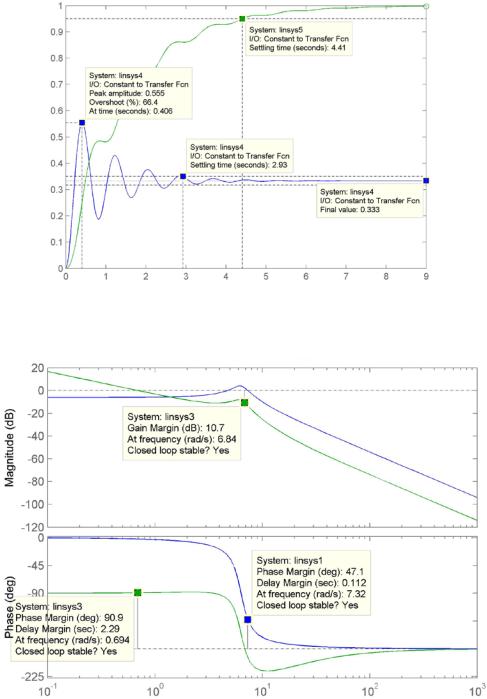
Проанализировав переходные характеристики в указанных диапазонах параметров ПИ-регулятора (7.32), выберем значения пара-
метров ПИ-регулятора, обеспечивающих минимальное значение q2. |
|||
Такими параметрами будут KП = 0,1 и KИ = 1,37. Ниже приведены ха- |
|||
рактеристики системы и карта нулей и полюсов синтезированной сис- |
|||
С |
|
|
|
темы управления. |
|
|
|
|
|
2 |
|
и1 |
|
||
б |
|||
|
|
А |
|
Рис. 7.1. Переходные временные характеристики системы управления: |
|||
1 – исходная система; 2 – синтезированная система |
|||
|
2 |
|
Д |
|
|
|
|
1 |
|
|
|
|
|
|
И |
Рис. 7.2. Частотные характеристики системы управления:
1 – исходная система; 2 – синтезированная система
48
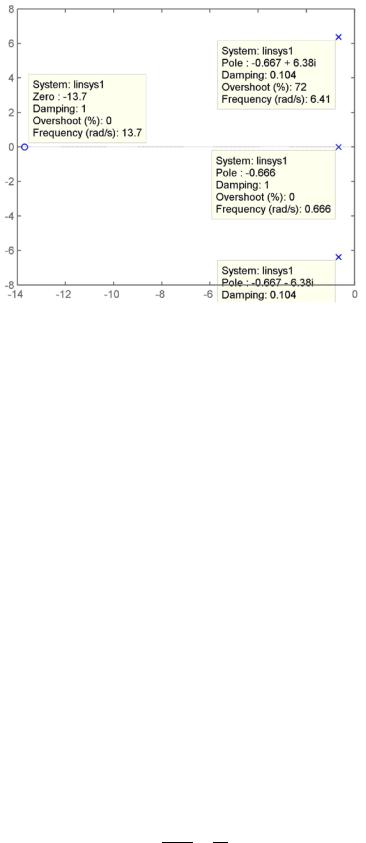
СРис
Выполнен е всех тре ований относительно численных показателей качества переходного процесса заставляет проектировщика искать компромисс в связиАс возникающим противоречием этих требований. Например, при увеличении коэффициента передачи ПИ-
. 7.3.бКарта нулей полюсов системы управления с ПИ-регулятором
регулятора KП увеличивается ыстродействие системы, т. е. уменьшается время переходного процесса tP, но появляется и нарастает колебательность переходного процесса μ. При дальнейшем увеличении коэффициента передачи до его критическогоДзначения по критерию
устойчивости системы значение колебательности возрастает до 100% (граница устойчивости незатухающий переходный процесс). Следо-
вательно, длительность переходного процесса tP → ∞.
Исходные данные для выполнения работы
Передаточная функция исходной разомкнутой системы управле-
ния имеет вид |
|
b0 |
|
И. (7.33) |
|
WРАЗ ( p) = |
|
|
|
||
a |
0 |
p2 +a p +a |
|||
|
|
1 |
2 |
|
|
Требуется синтезировать корневым методом параметры последовательного ПИ-регулятора:
WПИ ( p) = KП + KрИ = 1р(KП р+ KИ ).
При допустимой колебательности системы μ' = 10%.
49
|
Варианты параметров системы: |
|
|||||
1) |
b0 = 4; a0 |
= 2; a1 = 8; a2 = 2; |
2) |
b0 = 5; a0 = 1; a1 = 10; a2 = 1; |
|||
3) |
b0 = 4; a0 |
= 1; a1 = 8; a2 = 2; |
4) |
b0 = 1; a0 = 2; a1 = 10; a2 = 2; |
|||
5) |
b0 = 3; a0 |
= 1,5; a1 = 6; a2 = 0; |
6) |
b0 = 6; a0 = 3; a1 = 12; a2 = 3; |
|||
7) |
b0 |
= 3; a0 |
= 2; a1 = 10; a2 = 2; |
8) |
b0 = 3; a0 = 2; a1 = 6; a2 = 2; |
||
С |
|
10) |
b0 = 5; a0 = 5; a1 = 10; a2 = 2. |
||||
9) |
b0 |
= 4; a0 |
= 2; a1 = 8; a2 = 0; |
||||
|
|
|
|
|
Порядок выполнения работы |
||
|
1. |
Зап сать передаточную функцию и характеристическое урав- |
|||||
при |
|
|
|||||
нение замкнутой с стемы с ПИ-регулятором. |
|||||||
|
2. |
Определ ть максимально возможную степень устойчивости. |
|||||
|
3. |
Преобразовать характеристическое уравнение системы |
|||||
управлен я, выдел в з него множитель с корнем p3 = – ηmax. |
|||||||
|
4. |
|
колеб |
||||
|
Выяв ть уравнение, связывающее параметры ПИ-регулятора, |
||||||
|
которых дост гается максимальная степень устойчивости. |
||||||
|
5. |
Определ ть ограничение для коэффициента системы по до- |
|||||
пустимой |
|
ательности. |
|
|
|||
|
6. |
Определить дополнительного условия по корню полинома |
|||||
числителя. |
|
|
|
|
|||
|
7. |
Записать условияАоптимальных параметров ПИ-регулятора. |
|||||
8.Произвести вы ор оптимальных параметров ПИ-регулятора.
9.Получить в Simulink переходную временную характеристику и карту нулей и полюсов замкнутой исходной и синтезированной системы управления [2, 6].
10.Получить с помощью инструмента Linear Analysis в Simulink логарифмические частотные характеристики разомкнутой исходной и синтезированной системы управления [2, 6].
11.Сделать выводы по результатам синтеза.Д
Содержание отчетаИ
1.Название и цель работы.
2.Передаточная функция и характеристическое уравнение замкнутой системы с ПИ-регулятором.
3.Максимально возможная степень устойчивости ηmax.
4.Уравнения и ограничения полученные в процессе синтеза параметров ПИ-регулятора.
5.Условия оптимальных параметров ПИ-регулятора.
50
6. |
Значения выбранных оптимальных параметров ПИ-регулятора. |
7. |
Переходная временная характеристика и карта нулей и полю- |
сов замкнутой исходной и синтезированной системы управления. |
|
8. |
Логарифмические частотные характеристики разомкнутой ис- |
ходной и синтезированной системы управления. |
|
С |
|
9. |
Выводы по результатам синтеза. |
Вопросы задания для защиты лабораторной работы
1.Что такое с нтез автоматической системы управления?
2.Как е существуют корневые показатели качества и как их определ ть?
3.Зап ш те связь между прямыми и косвенными показателями качества регул рован я.
4.Пр вед те постановку задачи синтеза систем управления по корневым показателям качества.
5.Что называется оптимальной степенью устойчивости?
6.Поясн те основные шаги синтеза параметров системы корневым методом.
7.Как рассчитывается максимально возможная степень устой-
чивости?
8.Как получается ограничение по допустимой колебательности системы?
9.Какие обязательные и дополнительные условия накладываются на синтезируемые параметры системы в процессе синтеза?
10.Как производится схемная реализация корректирующего
звена и подбор параметров ПИ-регулятора в случае электромеханической аналоговой системы? Д
И
51

Лабораторная работа № 8
Построение фазового портрета системы
Цель работы − изучить метод анализа динамических свойств нелинейных автоматических систем управления по фазовому портрету.
Метод |
сследования динамики нелинейных АСУ с помощью |
|||
етсяизображающейточкой М. Процесс изменения состояния систе- |
||||
фазового пространства относится к наиболее ранним точным анали- |
||||
Стическ м методам теор и нелинейных систем. |
|
|||
Фазовое пространство – n-мерное пространство, образованное |
||||
системой коорд нат, состоящей из регулируемой величины x1 и её |
||||
б |
|
|||
производных ( с. 8.1, а) [1, 5, 7]. |
|
|||
Состоян е с стемы в таком фазовом пространстве представля- |
||||
мы представляет со ой некоторое движение изображающей точки M в |
||||
|
|
А |
|
|
фазовом пространстве [x1, x2, |
x3], который описывается фазовой тра- |
|||
екторией движения системы. Фазовая траектория показывает дина- |
||||
мику движения системы при ненулевых начальных условиях. Эти на- |
||||
чальные условия изо ражаются начальной точкой фазовой траекто- |
||||
рии M0 [1, 5, 7]. |
|
Д |
||
|
x3 |
|
||
а |
|
x2 |
б |
|
|
M |
|
|
M0(x10, x20) |
|
|
|
|
|
|
|
|
И |
|
|
|
x2 |
|
x1 |
|
|
M0 |
|
|
x1 |
|
|
|
|
|
|
Рис. 8.1. Фазовое пространство и траектории |
|
|
Фазовая плоскость – это двумерная координатная плоскость, в которой по осям координат откладываются две переменные (фазовые координаты): регулируемая величина x1 и её первая производная x2
(рис. 2.1, б) [1, 5, 7].
Совокупность фазовых траекторий для определенных начальных условий и состояний называется фазовым портретом системы.
52
Параметрические уравнения фазовой траектории для системы второго порядка представляют собой систему дифференциальных уравнений 1-го порядка в нормальной форме Коши [1, 5, 7]:
С |
|
|
x1 = a11 x1 +a12 x2 ; |
|
|
||||
|
|
|
|
|
|
|
|
(8.1) |
|
|
|
|
|
|
|
|
|
||
|
|
x2 = a21 x1 +a22 x2 . |
|
|
|||||
Данные уравнения получаются путём введения в исходное урав- |
|||||||||
нение с стемы новых переменных состояния xi(t) вместо (i – 1) произ- |
|||||||||
водных выходной вел чины y(t) |
|
|
|
|
|
|
|||
циальное |
= y ; |
x2 = y . |
|
(8.2) |
|||||
|
|
x1 = y ; x2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
Можно сключ ть из уравнений (8.1) время, |
разделив второе |
||||||||
уравнен е на первое, тогда получим (непараметрическое) дифферен- |
|||||||||
б |
|
|
|
||||||
уравнен е фазовых траекторий [1, 5, 7]: |
|
||||||||
|
x2 |
|
a21x1 + a22 x2 |
|
|
N(x1; x2 ) |
|
|
|
|
|
= |
|
|
= |
D(x1; x2 ) |
. |
(8.3) |
|
|
x1 |
|
a11x1 + a12 x2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Решен е уравнен я (8.3) x2 = f(x1) изображается на фазовой |
|
плоскости [x1; x2]. По оси а сцисс откладывается сама координата x1, а |
|
по оси ординат откладывается её первая производная x2. Каждой |
|
совокупности начальных условий (x10, x20) соответствуют свое реше- |
|
ние и своя фазовая траектория, которые образует фазовый портрет |
|
системы. |
Д |
Основные свойстваАфазовых траекторий [1, 5, 7]: |
|
1) если x2 = f(x1) определена и непрерывна в некоторой области |
|
и имеет непрерывные частные производные по своим аргументам, то |
|
фазовые траектории при различных начальных условиях не пересе- |
|
каются между собой; |
И |
|
|
2) при x2 > 0 координата x1 должна возрастать, поэтому в верхней фазовой полуплоскости изображающая точка движется слева направо, а в нижней полуплоскости движение происходит справа налево; 3) фазовые траектории пересекают ось абсцисс под прямым углом, за исключением особой точки, где dx2/dx1 = 0/0. Ось ординат фа-
зовые траектории могут пересекать под любым углом; 4) затухающему (устойчивому) переходному процессу соответ-
ствует фазовая траектория, сходящаяся к началу координат или отрезку покоя;
5) неустойчивому процессу соответствует фазовая траектория, удаляющаяся от начала координат.
53
Метод анализа и синтеза системы управления, основанный на построении фазового портрета, называют методом фазовой плоскости. Метод фазовой плоскости используется для исследования нелинейных систем, линейная часть которых описывается дифференциальным уравнением не выше второго порядка, а нелинейный элемент может быть любым.
Оценка устойчивости в методе фазовой плоскости опирается на одну из формулировок устойчивости А.М. Ляпунова.
Формул ровка устойчивости системы по Ляпунову: невозму- |
||
щенное дв жен е называется устойчивым по Ляпунову, если для лю- |
||
бого сколь угодно малого положительного числа ε найдется такое по- |
||
С |
|
расстояние |
ложительное ч сло δ, что в лю ой момент времени t ≥ t0 |
||
от изображающей точки фазовой траектории до начала координат фа- |
||
зовой плоскости х(t) меньше ε, при конечном начальном отклонении, |
||
т.е. при |х0(t0)| < δ [1, 5, 7]. |
|
|
при|х(t)| < ε |
t ≥ t0, если |х0(t0)| < δ. |
(8.4) |
б |
|
|
Невозмущенное движение системы называется асимптотически устойчивым по Ляпунову, если при конечном начальном отклонении |х0(t0)| < δ фазовая траектория стремится к началу координат при
Приведенным определениямАустойчивости можно дать следующую геометрическую интерпретацию. Пусть на фазовой плоскости
стремлении времени к есконечности. |
|
х(t) → 0 при t → ∞, если |х0(t0)| < δ. |
(8.5) |
Д |
|
[x1; x2] M0(x10; x20) – отклонение системы от заданного установившегося значения при t = 0 (рис. 8.1).
Это отклонение находится в пределах прямоугольника со сторонами 2δ1 и 2δ2. На плоскости показаны областиИ, в которых может находиться система, в виде трёх окружностей. Окружность радиуса r → 0 соответствует области асимптотической устойчивости, где отклонение движения х(t) → 0. Окружность радиуса ε соответствует области устойчивости с допустимым отклонением |х(t)| < ε. Окружность радиуса ρ соответствует недопустимому увеличению отклонения движения, при котором система становится неустойчивой. Три фазовых траектории демонстрируют три режима работы систем при определенном начальном отклонении |х0(t0)|. Первая траектория 1 соответствует асимптотически устойчивой системе, траектория 2 – устойчивой с допустимым отклонением и траектория 3 – неустойчивой системе [1, 5, 7].
54
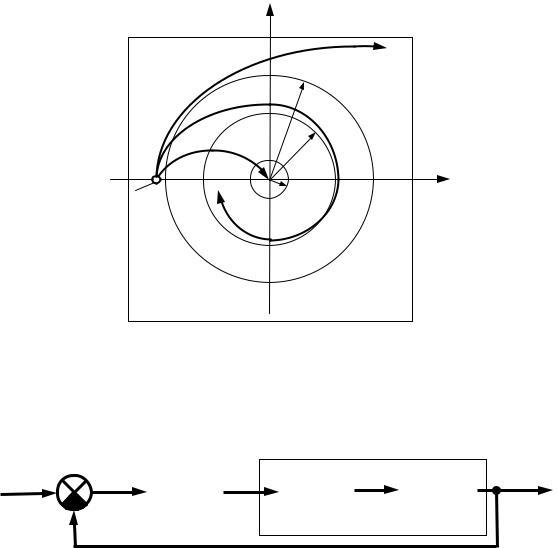
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
δ2 |
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
||
|
1 |
|
|
|
ε |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
M0(х10; х20) |
2 |
|
|
r |
|
|
δ1 |
x1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
траектории |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
б |
|
|
|
|
|
|
||||||||
|
Р с. 8.1. Фазовые |
|
|
|
устойчивых и неустойчивых систем |
|||||||||||
Пр мер. Дана нел нейная система управления (рис. 8.2) |
с релей- |
|||||||||||||||
ной характер ст кой F(x) о щего вида «Трехпозиционное реле с гисте- |
||||||||||||||||
|
|
|
А |
|
|
|
||||||||||
резисом» (см. прил. 3 та л. П.3, п. 9) [1, 5, 7]. |
|
|
|
|
|
|
||||||||||
u |
|
x |
НЭ |
|
|
z |
|
|
|
УУ |
φ |
|
|
ОУ |
|
y |
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
Д |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛЧ |
|
||
|
Рис. 8.2. Структурная схема нелинейной системы управления |
|
||||||||||||||
Уравнение линейной части системы ЛЧ, т.е. объекта управления |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
|||||
ОУ совместно с устройством управления УУ |
в операторной форме |
|||||||||||||||
имеет вид |
|
|
|
|
y(p) |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
WЛЧ ( |
р)= |
|
= |
(0,1р+1)р |
, |
|
|
|
(8.6) |
||||
|
|
|
|
|
|
z(p) |
|
|
|
|
|
|||||
а уравнение релейного регулятора – нелинейного элемента НЭ при входном воздействии u(t) = 0 описывается нелинейной функцией
z = F(x) = –F(y), |
(8.7) |
где x = –y и F(–y) = –F(y), так как нелинейная релейная характеристика нечётно-симметричная.
Уравнение релейного регулятора с характеристикой «Трехпозиционное реле с гистерезисом» приведено в табл. П.3, п. 9.
55
Параметры релейной характеристики: B = 1; b1 = 0,05; b2 = 0,1. Общее нелинейное дифференциальное уравнение свободной со-
ставляющей движения системы
0,1 |
d 2 y |
+ dy |
= −2F(y). |
(8.8) |
|
dt2 |
|||||
|
dt |
|
|
Запишем уравнение (8.8) в виде системы дифференциальных уравнений 1-го порядка, введя новые переменные состояния xi(t):
|
|
|
|
x1 = y , |
|
|
|
|
|
|
|
|
|
|
|
(8.9) |
|||||
|
|
|
|
x2 = y , |
x2 |
= y . |
|
|
|
|
|
||||||||||
Тогда модель с стемы в форме Коши будет иметь вид |
|
||||||||||||||||||||
С |
|
|
= x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
2 |
x2 |
|
2 |
|
|
|
|
|
|
|
|
|
(8.10) |
||
|
|
|
|
|
|
= − |
− |
|
|
F(x1 ). |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x2 |
0,1 |
0,1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
иОтсюда получ м дифференциальное уравнение фазовых траек- |
|||||||||||||||||||||
торий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
= |
−10x2 −20F(x1 ) |
|
|
|
|
= |
|
|
x2 |
|
|
|
(8.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
|
|
или x1 |
−10x |
|
− 20F(x |
) |
x2 . |
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
б1 2 |
|
1 |
|
|
|
|
||||||||||||||
ПроинтегрировавАего с помощью символьного интегрирования в
Matlab, получим уравнение фазовых траекторий
Всвязи с релейной функциейДрегулятора на фазовой плоскости [x1; x2] можно выделить три области: (1) FИ(x1) = –B; (2) F(x1) = 0;
(3)F(x1) = +B. Эти три области разделены и показаны штриховыми линиями переключения на рис. 8.3.
Вобласти (1) F(x1) = –B уравнение (8.12) принимает вид1 10 20
C1 = x10 +0,2ln[x20 −2]+0,1x20 . |
(8.14) |
В области (2) F(x1) = 0 уравнение (8.12) принимает вид |
|
x1 = −0,1x2 +C2 , |
(8.15) |
где C2 – коэффициент, зависящий от начальных условий x10 и x20.
56
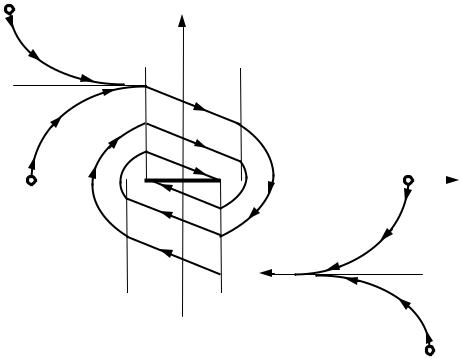
|
|
C2 = x10 +0,1x20 . |
(8.16) |
В области (3) F(x1) = +B уравнение (8.12) принимает вид |
|||
|
|
x1 = 0,2ln[x2 +2]−0,1x2 +C3 , |
(8.17) |
где C3 |
– коэффициент, зависящий от начальных условий x10 |
и x20. |
|
С |
C3 = x10 −0,2ln[x20 +2]+0,1x20 . |
(8.18) |
|
|
|
||
Фазовые траектор и в области (1) имеют асимптоту x2 = 2, к ко- |
||
торой они стремятся при увеличении x1. В области (3) фазовые траек- |
||
чины |
|
|
тории меют ас мптоту x2 = –2, к которой они стремятся при умень- |
||
шении x1. Данные ас мптот |
|
определяет максимальную скорость из- |
менен я выходной вел |
x1 при свободном движении системы. |
|
M03 |
б |
|
||||
|
|
|
|
|
||
|
|
|
|
x2 = y |
|
|
|
|
|
|
–0,05 |
+0,1 |
|
x2 |
= 2 |
|
|
(2) |
|
|
|
|
|
|
А |
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
M01 |
|
|
|
M02 |
|
(3) |
x1 = y |
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
x2 = –2 |
|
|
|
|
–0,1 |
+0,05 |
|
|
|
|
|
|
И |
|
|
|
|
|
|
ДM04 |
|
Рис. 8.3. Фазовый портрет нелинейной системы управления
В целом фазовые траектории принимают спиралевидную форму. Это соответствует затухающим колебательным процессам. Однако колебательный процесс не всегда затухает до нуля, а иногда до некоторого произвольного значения в интервале –0,05 ≤ x1 ≤ 0,05, x2 = 0, т.е. внутри зоны нечувствительности реле. Таким образом, вместо особой точки здесь получается особый отрезок равновесных состояний (отрезок покоя), показанный утолщенной линией на рис. 8.3.
57
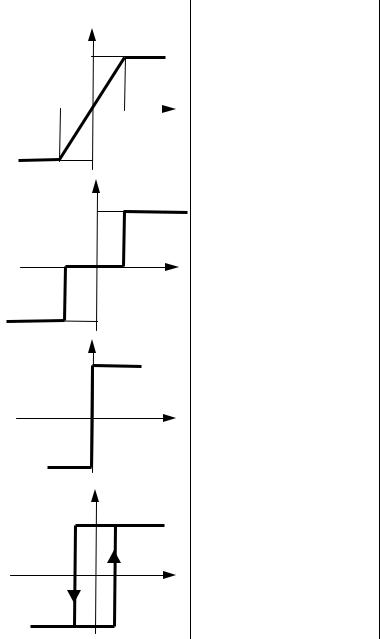
Исходные данные для выполнения работы
Заданная структурная схема модели нелинейной системы управ-
|
ления представлена на рис. 8.2. В табл. 8.1 представлены характери- |
||||||||||||||
|
стики, уравнения и параметры линейной и нелинейной частей нели- |
||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
нейной системы управления. Требуется построить фазовые портреты |
||||||||||||||
|
нелинейной системы управления и проанализировать её динамиче- |
||||||||||||||
|
ские свойства. |
|
|
|
|
|
|
|
|
|
|
|
Таблица 8.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Параметры л нейной и нелинейной частей системы |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
№ вар. |
Нел нейная часть |
Линейная часть |
Начальные условия |
|
||||||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бZ |
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
М0(0,5; 0); |
|
|
|
иW |
|
( |
р)= |
2 |
|
|
М0(1; 2); |
|
|||||
|
1 |
–0,5 |
|
|
|
ЛЧ |
|
|
|
|
р2 |
М0(2; 0); |
|
||
|
|
0 |
0,5 |
X |
|
|
|
|
|
|
|
|
|
М0(4; 4) |
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
М0(1; 0); |
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
||
|
2 |
–0,5 |
|
|
WЛЧ |
( |
р)= |
|
|
М0(0; 1); |
|
||||
|
|
|
|
|
Д5 |
|
|||||||||
|
|
0 |
0,5 |
X |
|
|
|
|
|
|
р2 |
М0(1; 1); |
|
||
|
|
|
А |
М0(–2; –2) |
|
||||||||||
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
И |
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
М0(0; 0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
WЛЧ ( |
р)= |
|
|
|
|
М0(1; 0); |
|
|||
|
|
|
|
|
р2 |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
М0(–2; 0); |
|
|||
|
|
|
X |
|
|
|
|
|
|
|
|
|
М0(4; –4) |
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
М0(0; 0); |
|
|
|
4 |
–0,5 |
|
|
WЛЧ (р)= |
|
|
|
|
М0(1; 0); |
|
||||
|
0,5 |
|
|
(0,2 р+1)р |
|
М0(2; 0); |
|
||||||||
|
|
0 |
X |
|
|
|
|
|
|
|
|
|
М0(–4; 4) |
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58

|
№ вар. |
Нелинейная часть |
Линейная часть |
Начальные условия |
|||||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
|
|
|
М0(0; 0); |
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
|
|
WЛЧ (р)= |
|
|
|
|
М0(1; 0); |
|||
|
|
|
|
(2 р +1)р |
|||||||||
С |
0 |
|
|
|
|
М0(2; 2); |
|||||||
|
X |
|
|
|
|
|
|
|
М0(–3; 3) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
3 |
|
|
|
М0(1; 0); |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
–0,5 |
|
|
|
WЛЧ (р)= |
|
|
|
|
|
М0(0; 1); |
||
|
|
|
(0,2 |
р +1)р |
|||||||||
|
|
|
0 |
0,5 |
X |
|
М0(1; 1); |
||||||
|
|
|
|
|
|
|
|
|
|
М0(–2; –2) |
|||
|
|
б |
|
|
|
|
|
|
|
||||
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
М0(2; 0); |
7 |
–0,5 |
|
|
|
WЛЧ (р)= |
|
|
3 |
|
|
|
М0(0; 2); |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
А |
М0(2; 2); |
||||||||
|
|
|
0 |
0,5 |
X |
|
(0,2 |
р +1)р |
|||||
|
|
|
|
|
|
|
|
|
|
М0(–2; –2) |
|||
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
Д |
|||||||
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
М0(1; 0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
–0,5 |
|
|
|
WЛЧ (р)= |
|
|
|
М0(1; –3); |
||||
|
|
|
р2 |
||||||||||
|
|
|
0,5 |
|
|
|
|
М0(–3; 0); |
|||||
|
|
0 |
|
X |
|
|
|
|
|
|
|
М0(3; 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Согласно математическому описаниюИ(табл. 8.1) и структурной схеме системы (см. рис. 8.2) получить параметрическое и дифференциальное уравнения фазовых траекторий системы.
2.Найти решения дифференциального уравнения фазовых тра-
екторий x2 = f(x1) для различных областей фазовой плоскости с учетом начальных условий.
3.Построить фазовый портрет системы с заданными начальными условиями.
59
|
Содержание отчета |
1. |
Название и цель работы. |
2. |
труктурная схема модели, передаточная функция линейной |
части и нелинейная характеристика нелинейной части системы. |
|
С |
|
3. |
Расчётные формулы, параметрическое и дифференциальное |
уравнения фазовых траекторий системы. |
|
4. |
Рассчитанные значения координат изображающей точки сис- |
темы управлен я с заданными начальными условиями М0(x10; x20). |
|
5. |
Фазовый портрет системы с заданными начальными усло- |
задания |
|
виями М0(x10; x20). |
|
6. |
Выводы о д намических свойствах нелинейной системы по |
фазовому портрету. |
|
Вопросы |
для защиты лабораторной работы |
||
1. |
Назов те в д типовых нелинейностей, представленных в |
||
табл. 8.1. |
А |
||
2. |
Что такое фазовая траектория и фазовый портрет? |
||
3. |
Перечислитебосновные свойства фазовых траекторий. |
||
4. |
Поясните процесс получения параметрического и дифферен- |
||
циального уравнений фазовых траекторий системы. |
|||
5. |
Какие особые точки соответствуют построенным фазовым |
||
траекториям? |
|
|
|
6. |
Что такое отрезок равновесных состояний? |
||
7. |
Какой вид фазовой траектории соответствует автоколеба- |
||
тельному режиму работы нелинейной системы управления? |
|||
8. |
|
|
И |
Как оценивают устойчивость в методе фазовой плоскости по |
|||
А.М. Ляпунову? |
|
Д |
|
9. |
Из каких соображений фазовую плоскость разбивают на не- |
||
сколько различных областей? |
|
||
60
Лабораторная работа № 9
Анализ устойчивости нелинейной системы прямым методом Ляпунова
СПрямой метод А.М. Ляпунова основан на построении специальных функц й (функц й Ляпунова) по исходным нелинейным диффеуравнен ям, описывающим поведение системы. Данные
Цель работы − изучить анализ устойчивости нелинейных авто-
матических систем управления прямым методом Ляпунова.
Общие сведения
скалярные функц , характеризуют динамические свойства нелинейной системы позволяют сделать вывод о её устойчивости [1, 5, 7].
В общем случае сво одное движение нелинейной динамической |
||||
ренциальным |
|
|
||
системы оп сывается системой дифференциальных уравнений со- |
||||
стояния 1-го порядка в форме Коши: |
|
|
||
|
|
= f1 (x1; x2 ;...xn ); |
|
|
x1 |
|
|
||
б |
|
|
||
|
|
= f2 (x1; x2 ;...xn ); |
|
|
x2 |
|
(9.1) |
||
|
|
|
|
|
... |
|
|
|
|
|
|
= fn (x1; x2 ;...xn ), |
|
|
|
xn |
|
|
|
А |
|
|||
|
|
Д |
|
|
где fi – нелинейные функции координат состояния, совокупность ко- |
||||
торых определяет направление движения изображающей точки M в |
||||
фазовом пространстве, т.е. вектор фазовой скорости f{x} = {f1; f2;…fn}. |
||||
|
|
|
И |
|
При этом fi определены и непрерывны в области |xi(t)| ≤ |
H, где |
|||
H – некоторая положительная постоянная, и обращаются в начале ко- |
||||
ординат в нуль [1, 5, 7]: |
|
|
|
|
|
|
fi (0;0;...0)= 0. |
|
(9.2) |
Функцией Ляпунова называется некоторая скалярная функция координат состояния V(x1; x2;…xn), которая принимает вещественные значения и удовлетворяет следующим свойствам [1, 5, 7]:
1)функция однозначная;
2)обращается в нуль при нулевых координатах V{0} = 0;
3)непрерывная вместе со своими частными производными в области |xi(t)| ≤ H, где H –некоторая положительная постоянная.
61
Функция Ляпунова V{x} называется знакоопределенной (опреде- ленно-положительной или определенно-отрицательной), если в области |xi(t)| ≤ H она принимает значение только одного знака и обращается в нуль только в начале координат. Например,
• |
определенно-положительная функция V = x2 |
+ x2 |
+ x2 ; |
||
|
|
|
1 |
2 |
3 |
• |
определенно-отрицательная функция V = −(x12 + x22 + x32 ). |
||||
Данные функции равны нулю только при x1 = x2 |
= x3= 0. |
||||
Функц я Ляпунова V{x} называется знакопостоянной (положи- |
|||||
тельной |
ли отр |
цательной), если в области |xi(t)| ≤ H она принимает |
|||
области |
|
|
|||
значен я только одного знака и обращается в нуль в конечном числе |
|||||
Сточек заданной |
фазового пространства. Например: |
||||
• |
V = (x − x |
)2 , V{x} = 0 при x1 = x2, в том числе и при x1 = x2= 0; |
|||
|
1 |
2 |
|
|
|
• |
V = (x − x |
)2 + x2 . V{x} = 0 при x1 = x2 и при x3= 0. |
|
||
|
1 |
2 |
3 |
|
|
Функц я Ляпунова V{x} называется знакопеременной, если в области |xi(t)| ≤ H она пр нимает значения разного знака и обращается в нуль в конечном ч сле точек заданной области фазового пространства. Например:
|
|
2 |
|
и при x3= 0. |
|
• V =бx + x + x . V{x} = 0 при x1 = –x2 |
|
||||
1 |
2 |
3 |
|
|
|
Такая функция для определения устойчивости системы по пря- |
|||||
мому методу Ляпунова не используется. |
|
|
|||
|
|
Д |
|
||
Наибольшее распространение для анализа широкого класса ли- |
|||||
нейных и нелинейныхАсистем получила функция Ляпунова в виде |
|||||
квадратичной формы (квадратичная функция) [1, 5, 7] |
|
||||
|
|
n |
n |
|
|
|
|
V {x}= ∑∑Pij xi xj , |
|
(9.3) |
|
|
|
i=1 |
j=1 |
И |
|
|
|
|
|
||
где Pij – постоянные коэффициенты.
Также квадратичную функцию Ляпунова можно представить в векторно-матричном виде [1, 5, 7]
(9.4)
P1n
. (9.5)
Pnn
Квадратичная форма функции Ляпунова (9.4) по критерию Сильвестра будет определенно-положительной, если каждый из е ё главных диагональных миноров будет положительным [1, 5, 7]:
∆ = P > 0; ∆ |
2 |
= |
|
P11 |
P12 |
|
> 0 и т.д. |
(9.7) |
||
|
|
|||||||||
С |
1 |
11 |
|
|
P21 |
P22 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Для систем, имеющих однозначную, непрерывную, нечётно- |
||||||||||
симметр чную нел нейность F(x), А.И. Лурье и В.М. Постниковым бы- |
||||||||||
ла предложена функц я Ляпунова как квадратичная форма от коорди-
нат состоян я л нейной части системы плюс интеграл от нелинейности: |
|||
функции |
|
x |
|
V {x}= x |
T |
Px + ∫F (x)dx . |
(9.8) |
0
Для анал т ческого решения задачи установления устойчивости
состав м про зводную |
|
Ляпунова по времени [1, 5, 7] |
|
||||||||||
dV = |
∂V dx1 + |
|
∂V dx2 |
+... + |
∂V |
|
dxn |
. |
(9.9) |
||||
|
∂x |
|
|
|
|||||||||
dt |
∂x dt |
|
∂x |
dt |
|
|
dt |
|
|||||
|
|
1 |
|
2 |
|
|
n |
|
|||||
|
А |
|
|||||||||||
Используя равенства (8.1), можно записать полную производную |
|||||||||||||
функции Ляпуновабпо времени, являющуюся общей функцией для сис- |
|||||||||||||
темы и функции Ляпунова V{x} [1, 5, 7]: |
|
|
|
|
|
||||||||
dV |
|
∂V |
|
|
∂V |
|
|
|
∂V |
|
|||
dt |
=W {x}= ∂x |
|
f1 + |
∂x |
f2 +... + |
|
|
fn . |
(9.10) |
||||
|
|
∂x |
|||||||||||
|
|
|
|
Д |
|
||||||||
|
|
1 |
|
2 |
|
|
|
|
n |
|
|||
Очевидно, что совокупность частных производных функции Ляпунова составляет градиент функции V{x}, т.е. вектор, определяемый
проекциями ∂V/∂xi на оси координат фазового пространства |
|
||||
|
∂V |
|
∂V |
И |
|
V = ∂V ; |
∂x2 |
;... |
|
. |
(9.11) |
∂x1 |
|
∂xn |
|
||
Тогда в результате произведения градиента функции Ляпунова
V{x} и вектора фазовой скоростиf{x} = {f1; f2…fn} получается тоже некоторая скалярная функция координат состояния системы [1, 5, 7]
dV |
=W {x}= V {x} f {x}, |
(9.12) |
dt |
|
|
где x – вектор координат состояния системы x = (x1; x2…xn).
Вектор V{x} перпендикулярен к поверхности V = const в каждой её точке x = (x1; x2…xn) и направлен в сторону возрастания значения функции Ляпунова V{x} (рис. 9.1).
63
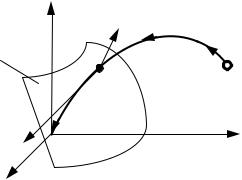
|
|
x3 |
V{x} |
|
|
|
|
|
|
x12 + x22 + x32 = С |
|
M |
M0 |
|
|
|
|
||
|
f{x} |
|
|
x2 |
|
|
|
|
|
|
|
x1 |
|
|
Р с. 9.1. Граф ческое представление градиента функции Ляпунова |
||||
полная про зводная функции Ляпунова W{x} > 0, то, со- |
||||
С |
|
|
|
|
Если |
|
|
|
|
гласно формуле (9.12), вектор фазовой скорости f{x} составляет с век-
тором V{x} острый угол, фазовая траектория пересекает поверхность V{x} = const в сторону увеличения значений V{x}. Если же W{x} < 0, то
уменьшен бя значен й V{x}. Уменьшение значений функции Ляпунова V{x} при пересечен её фазовой траекторией означает приближение последней к началу координатА, в случае знакоопределенной V{x}, или к некоему стационарному состоянию, в случае знакопостоянной V{x}, т.е. стремление устойчивой системы к состоянию равновесия.
угол между f{x} V{x} тупой и фазовая траектория идет в сторону
На основании вышеприведенных аналитических и графических заключений А.М. Ляпуновым ыли сформулированы следующие теоремы об устойчивости и неустойчивости нелинейных систем [1, 5, 7].
Теорема Ляпунова об устойчивости: если для системы, свобод-
ное движение которой описывается уравнениями (9.1), существует знакоопределенная функция V{x}, полная производная которой W{x} является знакопостоянной функцией противоположного знака, то
(9.1), существует знакоопределенная функция V{x}, полная производная которой W{x} является тоже знакоопределенной функцией противоположного знака, то система устойчива асимптотически.
система устойчива. |
Д |
|
|
Теорема Ляпунова об асимптотической устойчивости: если для |
|
системы, свободное движение которой описывается уравнениями |
|
|
И |
Теорема Ляпунова о неустойчивости: если для системы, сво-
бодное движение которой описывается уравнениями (9.1), существует какая-нибудь функция V{x}, полная производная которой W{x} является тоже знакоопределенной функцией и в любой сколь угодно малой области вокруг начала координат имеет знак, совпадающий со знаком V{x}, то система неустойчива.
64
Пример. Дана нелинейная система управления (см. рис. 8.2 лаб. работы № 8), имеющая однозначную нечётно-симметричную нелинейность с релейной характеристикой F(x1) общего вида «Идеальное трехпозиционное реле» (см. табл. П.3, п. 7). Параметры релейной характеристики: B = 1; b = 0,1. Необходимо провести анализ устойчиво-
сти прямым методом Ляпунова. |
|
|
||
С |
|
|
|
|
вободное движение нелинейной системы, заданное системой |
||||
дифференциальных уравнений состояния 1-го порядка в форме Коши: |
||||
|
x1 = x2; |
|
|
|
|
|
|
|
(9.13) |
|
|
x1 |
||
линейной x2 |
|
|||
|
x2 = −10x2 |
−20F(x1 ). |
|
|
где x1, x2 – фазовые координаты состояния системы.
По рекомендац ям А.И. Лурье и В.М. Постникова возьмем
функц ю Ляпунова как квадратичную форму от координат состояния |
||||
б |
1 |
2 |
||
части с стемы плюс интеграл от нелинейности: |
||||
V{x}= − |
2 |
− ∫F(x1 )dx1 . |
|
(9.14) |
40 |
0 |
|
|
|
Данная функция V{x} является определенно-отрицательной, так как она отрицательна c лю ыми значениями x и x (интеграл будет всегда положителен, так как функция F(x1) нечётно-симметричная) и обращается в нуль в начале координат.
Находим производную от функции Ляпунова по времени: |
|||||||||||||||||||
dV |
|
|
|
|
Дx |
||||||||||||||
|
|
|
|
|
|
dx |
|
x |
|
dx |
|
|
|
||||||
А1 2 2 |
|
||||||||||||||||||
dt = −F(x1 ) |
|
dt |
− |
20 |
|
dt |
. |
|
|
(9.15) |
|||||||||
Используя равенства (9.13), можно записать полную производ- |
|||||||||||||||||||
ную функции Ляпунова по времени: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
W{x}= −F(x |
)x |
|
− |
2 |
(−10x |
|
−20F(x |
))= |
|||||||||||
|
|
|
|||||||||||||||||
1 |
|
|
2 |
20 |
|
|
|
2 |
|
|
|
|
|
1 |
(9.16) |
||||
= −F(x )x |
|
|
|
x22 |
|
+ F(x |
)x |
|
|
|
x22 |
|
|||||||
2 |
+ |
|
2 |
= |
. |
|
|||||||||||||
|
|
|
|
||||||||||||||||
1 |
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
||||||
Так как полная производная W{x} являетсяИзнакоопределенной функцией противоположного V{x} знака, то система асимптотически
устойчива.
Таким образом, проведенный анализ системы методом Ляпунова позволяет оценивать влияние коэффициентов системы на её устойчивость и выявлять допустимые диапазоны значений коэффициентов для обеспечения устойчивости на этапе синтеза системы.
65
Исходные данные для выполнения работы
Исследовать прямым методом Ляпунова устойчивость положения равновесия систем управления, заданных системами дифференциальных уравнений состояния 1-го порядка в форме Коши:
1) |
|
|
|
= |
0,5x1 |
− |
x2 |
+ |
2x2 |
− |
3 |
2) |
x |
|
= −x + 2x3 ; |
|
|
|
|
|
|||||||
x1 |
|
|
|
|
x1 ; |
|
1 |
1 |
|
|
|
2 |
|
. |
|
|
|||||||||||
|
|
x = −2x − x . |
|
|
|
|
x = −2x − x − x |
|
|
||||||||||||||||||
|
|
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3) |
x1 |
= 2x2 − x1 |
|
|
|
|
4) |
x1 |
= 2x2 − x1 ; |
|
|
|
|
|
|||||||||||||
|
|
|
= −2x |
|
|
3 |
. |
|
|
|
|
|
|
= −x |
3 |
+ x . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
− x |
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
1 |
|
|
|
|
|
|
|
С |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
5) |
x1 |
= −x2 +0,5x1x2 ; |
|
|
6) |
x1 |
= −x2 +0,5x1x2 ; |
|
|
|
|||||||||||||||||
|
|
|
= −x − x |
2 |
x . |
|
|
|
|
|
|
= −x |
|
− x |
2 |
x |
|
3 |
. |
||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
− x |
|
||||||||||||||
|
|
|
2 |
|
1 |
1 2 |
|
|
|
|
|
|
2 |
1 |
1 2 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
; |
|
|
|
|
|
7) |
x1 |
= −x2 − x1 |
x2 ; |
|
|
|
8) |
x1 |
= −x2 − x2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= −x |
|
− x |
x |
− x |
. |
||||||||
иx = −x − x x . |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
1 |
|
1 2 |
|
|
|
|
|
|
2 |
1 |
|
1 2 |
|
2 |
|
|||||||
|
|
б |
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
; |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
||
|
x1 = −2x2 − x1 |
x2 |
|
|
|
x1 = −x1 − x2 |
|
|
|
|
|
||||||||||||||||
9) |
|
|
|
|
|
|
|
|
|
|
|
10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Выбрать квадратичную форму функции Ляпунова от коор- |
||||||||||||||||||||||||||
динат состояния системы управления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
||||||||||||
Найти производную от функции Ляпунова по времени. |
|||||||||||||||||||||||||||
3. |
Найти полную производную функции Ляпунова по времени. |
||
4. |
Исследовать полученную полную производную функции Ля- |
||
пунова по времени на знакопостоянство и знакоопределенность. |
|||
5. |
Сделать вывод об устойчивостиДсистемы управления. |
||
1. |
Название и цель работы. |
И |
|
2. |
Модель системы в форме Коши. |
||
|
|||
3. |
Расчётные формулы, квадратичная форма функции Ляпунова, |
||
производная от функции Ляпунова по времени, полная производная |
|||
функции Ляпунова по времени. |
|
||
4. |
Вычисления знакопостоянства и знакоопределенности пол- |
||
ной производной функции Ляпунова по времени. Выводы.
66
Вопросы и задания для защиты лабораторной работы
1. |
В какой форме представляется математическое описание |
|
системы для применения прямого метода Ляпунова? |
||
2. |
Что является функцией Ляпунова? |
|
3. |
Какие рекомендации по выбору функции Ляпунова сущест- |
|
вуют для линейных и нелинейных систем? |
||
4. |
Что значит знакоопределенность, знакопостоянство и знако- |
|
переменность функц |
Ляпунова? |
|
5. |
Как провер ть знакоопределенность функции Ляпунова в |
|
тической |
||
виде квадрат чной формы? |
||
С6. Что такое полная производная функции Ляпунова по времени? |
||
7. |
формул руйте теоремы Ляпунова об устойчивости, асимпто- |
|
|
устойч вости |
неустойчивости. |
8. |
б |
|
Что представляет со ой градиент функции Ляпунова? |
||
9. |
Что представляет со ой вектор фазовой скорости системы? |
|
10. |
Поясн те порядок расчета при оценке устойчивости нелиней- |
|
ной системы прямым методом Ляпунова.
А Д И
67
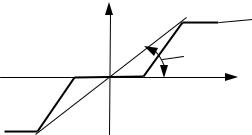
Лабораторная работа № 10
Анализ абсолютной устойчивости нелинейной системы частотным методом Попова
СнелинейностиЧастотный метод В.М. Попова применяется без линеаризации , поэтому является точным. При использовании метода
Цель работы − изучить анализ абсолютной устойчивости нелинейных автоматических систем управления частотным методом Попова.
Общие сведения
определяется абсолютная устойчивость системы с одной однозначной нечётно-с мметр чной нелинейностью.
Абсолютнаябустойчивость – это устойчивость в целом (при любых начальных условиях) нелинейной системы при нелинейной
характер ст ке, пр надлежащей к определенному классу [1, 5, 7].
Пусть в с стеме управления имеется лишь одна однозначная не- чётно-симметричная нелинейность, при этом конкретная форма её статической характеристики может ыть любая, в том числе нестабильная
с изменяющимися параметрами, но заданная в пределах угла от 0 до αf |
||
(рис. 10.1). При этом характеристическое уравнение линейной части |
||
системы А(p) = 0 имеет все корни с отрицательными вещественными |
||
|
Д |
|
частями или же кроме них имеется еще не более двух нулевых корней, |
||
что является условиемАприменимости критерия Попова [1, 5, 7]. |
||
Z |
|
Нелинейная |
|
характеристика |
|
|
|
И |
|
|
αf = arctg(kf) |
|
0 |
X |
Рис. 10.1. Однозначная характеристика нелинейного элемента
В методе Попова используется параметр kf – тангенс угла наклона линии, ограничивающей угол αf, к оси абсцисс.
Формулировка теоремы Попова: для установления абсолютной устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором при всех значениях частоты входного сигнала ω ≥ 0 будет справедливо неравенство [1, 5, 7]
68
Re(1+ jωh)W |
|
|
( jω) |
+ |
1 |
> 0 при 0 ≤ F (x) |
< k |
f |
x . |
(10.1) |
||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
ЛЧ |
|
|
|
|
k f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При наличии одного нулевого корня pi = 0 или an = 0 требуется |
||||||||||||||||||||||||
еще выполнение условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ImWЛЧ ( jω)→ −∞ при ω → 0 , |
|
|
|
|
|
|
(10.2) |
|||||||||||||||
а при двух нулевых корнях pi = pi+1 = 0 или an = an-1 = 0 |
|
|
|
|
|
|
||||||||||||||||||
С |
ReW |
ЛЧ |
( jω)→ −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
при |
ω→ 0 . |
|
|
|
|
|
|
(10.3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ImWЛЧ ( jω)< 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразовав левую часть неравенства (2.146), получим |
|
|||||||||||||||||||||||
Re(1+ jωh)W |
( jω) + |
1 |
=U |
ЛЧ |
(ω)−ωhV |
ЛЧ |
(ω)+ |
1 |
, |
(10.4) |
||||||||||||||
|
|
|||||||||||||||||||||||
|
|
ЛЧ |
|
|
|
|
k f |
|
|
|
|
|
|
|
|
k f |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где UЛЧ(ω) |
VЛЧ(ω) – действительная и мнимая части WЛЧ(jω). |
|
||||||||||||||||||||||
Пр равняв правую часть выражения (2.150) к нулю, получим |
||||||||||||||||||||||||
уравнен е прямой, проходящей через точку (–1/kf; j0) с наклоном 1/h, |
||||||||||||||||||||||||
называемой линией Попова [1, 5, 7]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б |
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
U |
ЛЧ |
(ω)−ωhV |
|
(ω)+ |
|
= 0. |
|
|
|
|
|
|
(10.5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ЛЧ |
|
|
|
k f |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из выражения (2.151) можно выделить модифицированную час- |
||||||||||||||||||||||||
тотную характеристикуАлинейной части системы W*ЛЧ(jω) путем ум- |
||||||||||||||||||||||||
ножения мнимой части исходной частотной передаточной функции |
||||||||||||||||||||||||
WЛЧ(jω) на частоту ω [1, 5, 7]: |
|
Д |
|
|||||||||||||||||||||
1.Если в исходной частотной передаточнойИфункции WЛЧ(jω) порядок полинома числителя не выше порядка полинома знаменате-
ля, то W*ЛЧ(jω) будет всегда лежать в конечной части плоскости. Это означает, что при ω → ∞ UЛЧ(ω) и ωVЛЧ(ω) стремятся либо к нулю, либо к конечному пределу.
2.Мнимая часть модифицированной частотной характеристики
ωVЛЧ(ω) в отличие от исходной VЛЧ(ω) является чётной функцией, следовательно, модифицированная частотная характеристика W*ЛЧ(jω) не будет симметричной относительно вещественной оси.(ω)+ jωV (ω)W * ( jω)=U (10.6)
69
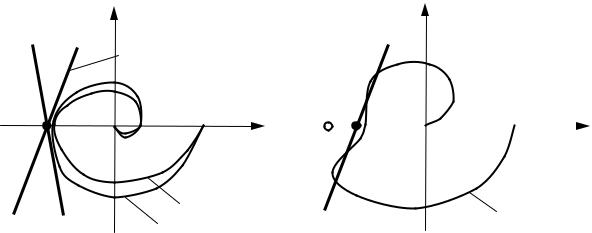
Графическая интерпретация теоремы Попова: для абсолют-
ной устойчивости нелинейной системы достаточно подобрать на комплексной плоскости [+1; j] такую прямую, проходящую через точку (– 1/kf; j0), где kf – угловой коэффициент нелинейной характеристики, чтобы вся кривая модифицированной частотной характеристики ли-
нейной части системы W*ЛЧ(jω) лежала справа от этой прямой [1, 5, 7]. |
|
С |
а показаны модифицированный годограф Найкви- |
На рис. 10.2, |
|
ста и линия Попова абсолютно устойчивой системы. Там же пунктирной лин ей показан немодифицированный годограф Найквиста. Эти годографы меют од наковые действительные части и, следовательно, пересекают действ тельную ось в одних и тех же точках. Мнимая часть эт х годографов разная, и модифицированный годограф пересекает мн мую ось при ольшем значении частоты, поэтому при мень-
шем абсолютном значении. |
|
|
|
||||
На |
с. 10.2, показан случай, когда условия абсолютной ус- |
||||||
тойчивости В.М. Попова не выполняется. Через точку (–1/kf; j0) нель- |
|||||||
зя |
л н ю Попова так, |
она не пересекала модифици- |
|||||
провести |
|
|
|
||||
рованный годограф Найквиста. Однако через точку (–1/kf*; j0) можно |
|||||||
провести нужную прямую Попова (пунктирная линия). Система с та- |
|||||||
кой нелинейной характеристикой, ограниченной углом αf* = arctg(kf*), |
|||||||
будет устойчивой. |
|
|
|
|
|
||
|
чтобы |
|
|
||||
|
jV(ω) |
|
а |
|
jV(ω) |
б |
|
|
|
Линия Попова |
|
|
|
||
|
|
|
|
А |
|
|
|
–1/kf |
|
|
|
ω = 0 |
–1/kf* |
ω = 0 |
|
|
|
|
|
U(ω) |
–1/kf |
|
U(ω) |
|
|
|
|
W*ЛЧ(jω) |
Д |
|
|
|
|
|
|
|
W*ЛЧ(jω) |
||
|
|
|
|
WЛЧ(jω) |
|
|
|
|
Рис. 10.2. Графическая интерпретация теоремы Попова |
|
|||||
Сравним условие абсолютной устойчивостиИВ.М. Попова с ус- |
|||||||
ловием устойчивости линейной системы по критерию Найквиста. Ес- |
|||||||
ли для нелинейности, лежащей в секторе (0; αf) произведем линеаризацию в виде y = hx, то введя такое звено в частотную характеристику Попова, получим точный аналог критерия Найквиста. Только критической точкой, которую не должна охватывать частотная характеристика Попова, будет точка с координатами (–1/kf; j0) [1, 5, 7].
70
Пример. Дана нелинейная система управления (см. рис. 8.2 лаб. работы № 8), имеющая однозначную нечётно-симметричную нелинейность «Идеальное трехпозиционное реле» (см. табл. П.3, п. 7). Выходная величина реле B = 0,33, порог срабатывания b = 1.
|
|
Линейная часть описывается передаточной функцией |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
( p) = |
|
|
|
|
6 |
|
|
|
|
|
1 |
e−0,5 p . |
|
|
|
|
|
(10.7) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛЧ |
|
|
|
|
(0,5 p +1) p |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Зап шем частотную характеристику линейной части системы |
|||||||||||||||||||||||||||||||||||||||||||
характеристики |
6 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
С |
|
W |
|
( jω) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
e−0,5 jω . |
|
|
|
(10.8) |
|||||||||||||||||||||||
|
|
(0,5 jω + |
|
1) jω |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
ЛЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Выдел м действ тельную UЛЧ(ω) и мнимую VЛЧ(ω) части ис- |
|||||||||||||||||||||||||||||||||||||||||||
ходной частотной |
|
|
|
|
|
|
|
|
|
|
|
|
|
WЛЧ(jω). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
W |
|
|
( jω) = |
|
|
|
|
6 |
|
|
|
1 |
|
e−0,5 jω = |
|
|
6(0,5 jω−1) |
|
− j e−0,5 jω = |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
ЛЧ |
|
|
|
(0,5 jω+1) jω |
|
|
|
|
|
|
((0,5 jω) |
|
−12 ) ω |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
6 |
( |
0,5 jω−1 |
) |
j |
|
А |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
− ω− |
6 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
e−0,5 jω = |
|
|
|
|
3 |
|
|
|
|
|
(cos(0,5ω)− jsin (0,5ω))= |
|
||||||||||||||||||||
|
( |
|
|
|
|
|
б) ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
0,25ω +1 |
|
ω |
|
|
|
|
|
|
0,25ω +1 ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
−3ωcos(0,5ω)− j6cos(0,5ω)+ j3ωsin (0,5ω)−6sin (0,5ω) |
= |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25ω2 +1 ω |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||||||||||||||||
|
|
= − |
3ωcos(0,5ω)+6sin (0,5ω) |
+ j |
3ωsin |
(0,5ω)−6cos(0,5ω) |
. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
||
|
|
Так как характеристическое уравнение линейной части системы |
|||||||||||||||||||||||||||||||||||||||||||
имеет один нулевой корень, то требуется выполнение условия (10.2): |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||
|
|
|
|
|
|
ImW |
(0) |
= |
3 0 sin (0,5 0)−6cos(0,5 |
0) |
= |
−6 → −∞. |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ЛЧ |
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25 02 +1 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Модифицированная частотная характеристика линейной части |
|||||||||||||||||||||||||||||||||||||||||||
системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
WЛЧ* |
( |
jω)= − |
3ωcos(0,5ω)+6sin (0,5ω) |
|
+ j |
3ωsin (0,5ω)−6cos( |
0,5ω) |
. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
( |
0,25ω2 |
+1 |
) |
ω |
|
|
|
|
|
|
|
|
|
( |
0,25ω2 +1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
||||||
Определим параметр kf – тангенс угла наклона линии, ограничивающей нелинейную характеристику, kf = 0,33/1 = 0,33 (рис. 10.3).
71

|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
0,33 |
|
|
|
|
αf = arctg(kf) |
||
|
|
|
|
–1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
X |
||
|
|
|
|
|
–0,33 |
|
|
|
|
|
|
|
Рис. 10.3. Определение углового коэффициента нелинейной характеристики |
||||||||||||
и |
|
|
4,0 |
|
|
jV(ω) |
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
С |
Л н я Попова |
|
|
|
|
|
|
|||||
|
–1/kf |
|
|
2,0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
U(ω) |
|
||||||
-6,0 |
|
-4,0 |
-2,0 |
0,0 |
|
|
||||||
|
|
|
|
|
W*ЛЧ(jω) |
-2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
-4,0 |
|
|
|
|
|
||
|
|
|
WЛЧ(jω) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
-6,0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
ω |
ω |
А |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.4. Графическое решение метода Попова |
||||||||||
|
|
|
|
|
Д |
|||||||
После определения всех необходимых параметров и характери- |
||||||||||||
стик можно построить на комплексной плоскости [+1; j] исходную и |
||||||||||||
модифицированную частотные характеристики линейной части сис- |
||||||||||||
темы WЛЧ(jω) и W*ЛЧ(jω), а также линию Попова, проходящую через |
||||||||||||
точку (–3; j0) |
(рис. 10.4), что определяет абсолютную устойчивость |
|||||||||||
нелинейной системы. |
|
|
И |
|||||||||
|
|
|
|
|
|
|
|
|||||
Исходные данные для выполнения работы
Заданная структурная схема модели нелинейной системы управления представлена на рис. 8.2 лаб. работы № 8. В табл. 10.1 пре д- ставлены характеристики и уравнения с параметрами линейной и нелинейной частей нелинейной системы управления. Согласно сектору, определяющему границы однозначной нечётно-симметричной нелинейной характеристики, и математическому описанию линейной части системы провести анализ абсолютной устойчивости частотным методом Попова.
72
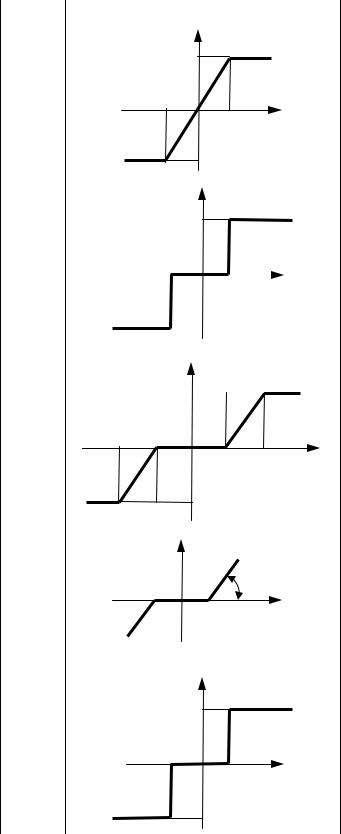
Таблица 10.1
Параметры линейной и нелинейной частей системы
|
№ вар. |
Нелинейная часть |
|
|
|
|
|
Линейная часть |
|
|||||||||||||||
С |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,5 |
|
|
|
|
WЛЧ |
(р)= |
|
|
|
|
1 |
|
|
e−0,5 p |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
–0,25 |
|
|
|
|
|
(0,1 |
р+1)р |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 0,25 |
|
|
|
WЛЧ |
(р)= |
|
|
|
|
1,2 |
|
|
e−0,6 p |
|
|||||||||
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
(0,2 |
р+1)р |
|
|||||||||||||||
|
|
|
|
|
–0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
(р)= 0,5(2 p +1) |
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
W |
|
|
|||||||||||
|
|
б |
|
|
|
|
ЛЧ |
|
|
|
|
(0,5 p +1)2 |
|
|||||||||||
2 |
–0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1(1p +1) |
|
||||||||
|
и0,1 |
X |
|
|
|
|
W |
(р)= |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
ЛЧ |
|
|
|
|
(0,5 p +1)2 |
|
|||||||
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
WЛЧ (р)= |
|
|
|
0,5 |
|
|
e−0,25 p |
|
||||||||
3 |
–0,25 –0,05 |
|
|
|
|
(0,5 р+1) |
р |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
W |
|
(р)= |
|
|
|
|
0,5 |
|
|
e−0,5 p |
|
|||||||||
|
|
|
|
0 |
0,05 0,25 |
X |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ЛЧ |
|
|
|
|
р+1)р |
|
|||||||||||||
|
|
|
|
А(0,1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Z |
Z |
|
|
|
|
|
И |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
W |
|
|
(р)= |
|
|
|
|
10 |
|
|
e−0,2 p |
|
|||
|
|
|
|
|
arctg0,5Д |
|
||||||||||||||||||
4 |
–0,5 |
|
|
|
|
|
|
|
ЛЧ |
|
|
(0,2 |
р+1)р |
|
|
|
|
|||||||
|
|
|
0 |
|
0,5 |
X |
|
|
WЛЧ |
(р)= |
|
|
|
|
15 |
|
|
e−0,5 p |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0,2 |
р+1)р |
|
|
|
|
|||||
|
|
|
|
20 |
|
|
|
|
WЛЧ |
(р)= |
|
|
|
0,05 |
|
|
e−0,5 p |
|
||||||
5 |
–0,5 |
|
|
|
|
|
(0,1р+1)р |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
WЛЧ ( |
р)= |
|
0,075 |
|
|
|
e−1 p |
|
||||||||||||
|
|
|
|
|
0 0,5 |
X |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
(0,1р+1)р |
|
||||||||||||||||
|
|
|
|
|
–20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73
|
Порядок выполнения работы |
|
1. |
Согласно исходным данным (табл. 10.1) определить тангенс |
|
угла наклона линии, ограничивающей сектор нелинейной характери- |
||
стики, к оси абсцисс. |
|
|
С |
|
|
2. |
При наличии нулевого корня характеристического уравнения |
|
линейной части системы проверить выполнение условия (10.2). |
||
3. |
Выделить действительную и мнимую части исходной час- |
|
тотной характер ст ки линейной части системы и записать модифи- |
||
|
частотную характеристику линейной части системы. |
|
цированную |
||
4. |
Постро ть на комплексной плоскости исходную и модифи- |
|
|
частотные характеристики линейной части системы. |
|
5. |
Провести на той же комплексной плоскости линию Попова. |
|
6. |
делать вывод |
а солютной устойчивости системы управ- |
ления. |
об |
|
|
|
|
Содержание отчета
части и нелинейная характеристикаАнелинейной части системы.
1. Название и цель ра оты.
2. Структурная схема модели, передаточные функции линейной
3.Расчётные формулы и производимые по работе вычисления.
4.Графики исходной и модифицированной частотной характеристики линейной части системы и линии Попова.
5.Выводы об абсолютной устойчивости системы управления.
Вопросы и задания для защитыДлабораторной работы
1.Какие виды нелинейных характеристик позволяют использовать частотный метод Попова?
2.Что такое абсолютная устойчивость системы?
3.Сформулируйте теорему Попова.
4.Что называется линией Попова?
5.Что в плане линейной части системы является условиемИ
применимости критерия Попова?
6.Как получить модифицированную частотную характеристику линейной части системы?
7.Какова графическая интерпретация теоремы Попова?
8.Как определяется угловой коэффициент нелинейной характеристики?
74
Лабораторная работа № 11
Анализ автоколебаний нелинейной системы
Цель работы − изучить алгебраический метод анализа автоко- С
лебаний в нелинейных автоматических систем управления.
Общие сведения
Алгебра ческ й метод определения автоколебаний в нелинейлениеных с стемах предлож л советский ученый Е.П. Попов. Данный метод пр меняется для с стем высокого порядка (выше 2-го). Опреде-
с мметр чных автоколе аний алгебраическим методом основано на гармон ческой линеаризации нелинейности и определении границ устойч вости л неаризованной системы [5, 7].
Пусть автомат ческая система (см. рис. 8.2 лаб. работы № 8 ) с одной нел нейностью F(x) имеет передаточную функцию линейной
части, обладающую свойством фильтра низких частот: |
|
|||||||||
|
А |
|
||||||||
бW (p)= |
R(p) |
. |
|
|
(11.1) |
|||||
|
|
|
|
|
||||||
Q(p) |
|
|||||||||
|
|
ЛЧ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Уравнения линейной части системы и нелинейного звена при |
||||||||||
|
|
Д |
|
|||||||
входном воздействии u(t) = 0 в операторной форме: |
|
|||||||||
|
Q(p)y = R(p)z; |
|
(11.2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
z = F(x) = −F(y). |
|
|
|||||||
Тогда уравнение замкнутой |
системы в операторной форме |
|||||||||
примет вид |
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(p)y = −R(p)F(y). |
(11.3) |
||||||||
Возможные автоколебания выходной величины с частотой ω' и |
||||||||||
амплитудой А' запишем как периодическое решение |
|
|||||||||
|
|
′ |
|
′ |
|
|
|
|
|
(11.4) |
|
|
y = А sin ω t . |
|
|
|
|||||
После гармонической линеаризации нелинейного элемента его |
||||||||||
уравнение в операторной форме имеет вид |
|
|
||||||||
|
|
|
|
′ |
p |
|
|
|||
|
|
|
|
|
|
|
y , |
(11.5) |
||
|
z = − q(A) +q (A) |
|
|
|
||||||
|
|
|
|
|
ω |
|
|
|||
75
где коэффициенты гармонической линеаризации q(A) и q'(A) для различных типов нелинейностей представлены в табл. П.4 прил. 4.
Тогда уравнение замкнутой системы (11.3) с учетом уравнения (11.5) в операторной форме примет вид [5, 7]
|
|
′ |
p |
|
|
С |
|
|
у = 0. |
(11.6) |
|
Q(p)+R(p) q(A) +q (A) |
|
||||
|
|
|
ω |
|
|
Поскольку в скомом решении уравнения А' = const и ω' = const, |
|||||
то гармон чески |
л неаризованное |
уравнение замкнутой |
системы |
||
(11.6) можно рассматр вать как обыкновенное линейное уравнение с постоянными коэфф ц ентами. Специфика его состоит лишь в том, что не звестные постоянные коэффициенты, зависящие от искомого решен , что и позволит нам получить решение со специфическ ми свойствами, присущими нелинейной системе.
Периодическое решение уравнения (11.6) соответствует паре чисто мнимых корней p1,2 = ± jω характеристического уравнения (11.8) [5, 7]. Поэтому для отыскания этого решения перейдем в час-
Зап шем характеристическое уравнение гармонически линеари- |
||||
зованнойимеютсяс стемы [5, 7] |
p |
|
||
|
|
|||
Q(p)+R(p) q(A) +q′(A) |
|
|
= 0 . |
(11.7) |
ω |
||||
|
|
|
|
|
Заметимб, что решение задачи упрощается в случае однозначной |
||||
нелинейности, когда мнимый коэффициент гармонической линеари- |
||||
зации q' (A) = 0. Тогда, согласно (11.7) имеем |
|
|
||
Q(p)+ R(p)q(A) = 0 . |
|
(11.8) |
||
А |
|
|||
Д |
|
|||
|
И |
|
тотную область, заменив оператор p = jω. Получим |
|
|
|
Q(jω)+R(jω)q(A) = 0 . |
(11.8) |
Выделим в этом выражении вещественную и мнимую части в |
||
виде [5, 7] |
U (A,ω)+ jV (A,ω)= 0 . |
(11.9) |
|
||
В результате получим два алгебраических уравнения, из которых и определяются искомые амплитуда А' и частота ω' периодического решения [5, 7].
U (A,ω)= 0; |
(11.10) |
V (A,ω)= 0. |
|
|
|
76
Сначала из второго уравнения определяется частота ω' периодического решения, а затем, если найдено вещественное значение ω', из первого уравнения определяется амплитуда А'. Видно, что частота автоколебаний зависит только от параметров линейной части системы и не зависит от формы однозначной нелинейности [5, 7].
Пример. Дана нелинейная система управления (см. рис. 8.2 лаб. работы № 8), имеющая однозначную нечётно-симметричную нелинейность «Идеальное трехпозиционное реле» (см. табл. П.3, п. 7). Па-
раметры релейной характеристики: B = 2; b1 |
= 0,05. |
|
|||||||||||
Уравнен е л нейной части системы управления в операторной |
|||||||||||||
нелинейной |
|
|
|
|
|
|
|
|
|
|
|
|
|
форме |
меет в д |
|
|
|
|
|
|
|
|
|
|
|
|
СWЛЧ (р)= |
y(p) |
= |
|
|
|
|
2 |
|
|
, |
(11.11) |
||
|
|
z(p) |
(0,1р +1)2 р |
|
|
||||||||
а |
функци |
|
|
|
|
|
|
|
|
|
|
|
|
|
z = F(x) = –F(y), |
|
|
|
(11.12) |
||||||||
где x = –y F(–y) = –F(y), так как нелинейная релейная характеристи- |
|||||||||||||
ка нечётно-с мметр чная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|||||||||||
Уравнение сво одной составляющей замкнутой системы в опе- |
|||||||||||||
раторной формебпри u(t) = 0 удет иметь вид |
|
|
|
||||||||||
|
(0,1р+1)2 рy(p)= 2z(p). |
|
|
(11.13) |
|||||||||
|
|
Д |
|||||||||||
После гармонической линеаризации нелинейного элемента его |
|||||||||||||
уравнение в операторной форме имеет вид |
|
|
|
|
|||||||||
|
|
|
8 |
|
|
|
2 |
|
|
2 |
|
|
|
|
z = −q(A)y = − |
πA2 |
|
A |
|
−0,05 |
|
y . |
(11.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
И |
|||
Тогда уравнение замкнутой гармонически линеаризованной сис- |
|||||||||||||
темы (11.16) с учетом уравнения (11.17) примет вид |
|
||||||||||||
|
0,01р3 y +0,2 р2 y + рy + 2q(A)y = 0 . |
(11.15) |
|||||||||||
Запишем характеристическое уравнение гармонически линеари- |
|||||||||||||
зованной системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01р3 +0,2 р2 + р+2q(A)= 0. |
(11.16) |
|||||||||||
Перейдем в частотную область, заменив оператор p = jω |
|
||||||||||||
|
0,01(jω)3 +0,2(jω)2 + jω+2q(A)=. |
(11.17) |
|||||||||||
|
−0,01 jω3 −0,2ω2 + jω+2q(A)= 0 |
|
|||||||||||
77
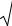
Система уравнений, дающая искомое периодическое решение:
|
2 |
+ 2q(A)= 0; |
|
− 0,2ω |
|
(11.18) |
|
|
|
3 |
|
|
|
|
|
− 0,01ω + ω = 0. |
|
||
Из второго уравнения (11.18) определяем частоту периодического решения ω' = 10 рад/с, а из первого уравнения определяется амплитуда А':
|
|
|
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
2 |
|
|
|
2 |
(11.19) |
||||
|
|
− 0,2 |
10 |
|
− 2 |
|
|
|
|
− |
0,05 |
|
= 0 . |
|||
|
|
|
πA2 |
|
|
|||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4 |
|
2 |
|
|
|
2 |
|
|
|
|
||||
15,42A − A +0,05 |
|
= 0 . |
|
(11.19) |
||||||||||||
|
|
|
|
|
||||||||||||
Решен ем данного |
|
иквадратного уравнения является пара со- |
||||||||||||||
пряженных вещественных корней А1,2 = ±0,051 и А3,4 = ±0,2495. |
|
|||||||||||||||
Так |
|
, в исследуемой нелинейной системе управления |
||||||||||||||
имеютсякак н мум два автоколебательных режима с частотой |
||||||||||||||||
ω' = 10 рад/с |
ампл тудами 1' = 0,051 и |
|
2' = 0,2495, зависящими от |
|||||||||||||
начальных услов й переменных состояния системы. |
|
|||||||||||||||
|
образом |
|
|
|
|
|
|
|||||||||
|
Исходные данные для выполнения работы |
|
||||||||||||||
Заданная структурнаяАсхема модели нелинейной системы управления представлена на рис. 8.2 лабД. работы № 8. В табл. 11.1 пре д- ставлены характеристики и уравнения с параметрами линейной и нелинейной частей нелинейной системы управления.
Требуется определить наличие в нелинейной системе управле-
1.Согласно исходным данным составитьИуравнение свободной составляющей замкнутой системы в операторной форме.
2.Записать характеристическое уравнение гармонически линеаризованной замкнутой системы управления.
3.Записать характеристическое уравнение системы управления
вчастотной форме.
4.Выделить вещественную и мнимую части характеристиче- ского уравнения системы управления в частотной форме.ния симметричных автоколебаний алгебраическим методом и пара-
78

5.Составить систему уравнений для определения частоты и амплитуды периодического решения.
6.Вычислить параметры А' и ω' имеющихся автоколебательных режимов.
С |
|
|
|
|
|
|
|
|
|
|
Таблица 11.1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Параметры линейной и нелинейной частей системы |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
№ п/п |
Нел нейная часть |
|
|
|
Линейная часть |
|
|||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Z |
|
|
|
|
|
WЛЧ (р) |
|
|
|
5 |
|
|
|
|
|
|
1 |
+2 |
|
|
|
|
|
= |
(0,1p +1)( p +1) p |
|
||||||||
|
|
|
|
0 |
|
X |
|
WЛЧ (р)= |
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
(0,1p +1)(0,1p +1) p |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
+2 |
|
|
|
|
|
|
WЛЧ (р) |
= |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(0,1p +1)( p +1) p |
|
|||||||||
|
2 |
–0,1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 0,1 |
X |
|
|
WЛЧ ( |
р)= |
5 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(0,1p +1)2 p |
|
|||||||||||
|
|
б |
|
|
|
|
|
|
||||||||||
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Д |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
WЛЧ ( |
р)= |
(0,1p +1)2 p |
|
|||||||
|
3 |
–0,5 |
А |
2 |
|
|
|
|
|
|||||||||
|
|
|
|
0 |
0,5 |
X |
|
WЛЧ (р)= |
|
(0,25 p2 +0,5 p +1) p |
|
|||||||
|
|
|
|
–1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
И |
|
||||||||
|
|
+1 |
|
|
|
|
|
|
WЛЧ ( |
р)= |
5 |
|
|
|
|
|
||
|
4 |
–0,5 |
|
|
|
|
|
|
|
|
|
|
(0,1p +1)2 p |
|
||||
|
|
|
|
0 0,5 |
X |
|
WЛЧ (р)= |
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
(0,25 p2 +0,5 p +1) p |
|
|||||||||||
|
|
|
|
–1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
WЛЧ (р)= |
|
|
2 |
|
|
|
|
|
||
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(0,1p2 +0,5 p +1) p |
|
|||||||||||
|
5 |
–1 |
|
|
|
|
|
|
|
|
||||||||
|
0 |
1 |
|
|
|
WЛЧ (р) |
= |
|
30 |
|
|
|
|
|
||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
(0,1p +1)( p +1) p |
|
|||||||||||
|
|
|
|
–0,5 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79
|
|
Содержание отчета |
1. |
Название и цель работы. |
|
2. |
труктурная схема модели, передаточные функции линейной |
|
части и нелинейная характеристика нелинейной части системы. |
||
3. |
Расчётные формулы и производимые по работе вычисления, |
|
в том числе система уравнений, дающая искомое периодическое |
||
решение. |
|
|
4. |
Ч сленные значения параметров А' и ω' имеющихся автоко- |
|
лебательных реж мов. |
|
|
5. |
Выводы по анализу автоколебаний в нелинейных системах. |
|
С |
|
|
Вопросы задания для защиты лабораторной работы |
||
1. |
В чем суть гармонической линеаризации? |
|
2. |
Чему равен |
коэффициент гармонической линеари- |
мнимыйб зации в случае однозначной нелинейности?
3.В чем суть алге раического метода определения автоколебаний в нелинейной системе?
4.В каком случае можно применить алгебраический метод определения автоколебаний в нелинейной системе?
5.Какой тип корней характеристического уравнения системы позволяет определить автоколебания?
6.Как получить гармонически линеаризованное уравнениеА
замкнутой системы? |
Д |
7. От чего зависит частота автоколебаний в случае однозначной |
|
нелинейности? |
И |
|
|
80
Лабораторная работа № 12
Определение границ абсолютной устойчивости нелинейной системы
Цель работы − изучить методику определения границ абсолютной устойчивости нелинейных автоматических систем управления.
Общие сведения
симметр |
||
В нел нейной с стеме управления может существовать такая |
||
Собласть параметров л нейной части, которая обеспечивает абсолют- |
||
ную устойч вость в независимости от конкретной формы нелинейной |
||
характер |
ст ки. |
|
Для |
обладает |
|
нел нейных систем с одной однозначной нечётно- |
||
|
чной нел нейностью, у которых передаточная функция ли- |
|
нейной части |
свойством фильтра низких частот, можно опре- |
|
делять устойч |
вость как свойство затухания переходных процессов. |
|
|
|
А |
Граница устойчивости может ыть определена как граница области существования периодических со ственных колебаний в системе, т.е. как граница появления пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы [1, 5, 7].
Пусть автоматическая система (см. рис. 8.2 лаб. работы № 8 ) с |
||||
Д |
|
|||
одной однозначной нечётно-симметричной нелинейностью F(x) имеет |
||||
передаточную функцию линейной части |
|
|
||
WЛЧ (p)= |
R(p) |
. |
|
(12.1) |
|
Q(p) |
И |
||
Заметим, что характеристическое уравнение системы при гар- |
||||
монической линеаризации нелинейной зависимости, в случае одно- |
||||
значной нелинейности F(x) (q' (A) = 0), имеет вид |
|
|||
Q(p)+ R(p)q(A) = 0. |
(12.2) |
|||
Наличие пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы можно определить по критерию Гурвица. При их наличии последний определитель
Гурвица n−1 = 0, а остальные определители положительные при любых возможных значениях q(A) (для систем третьего и четвертого порядка это означает просто положительность коэффициентов характеристического уравнения) [1, 5, 7].
81
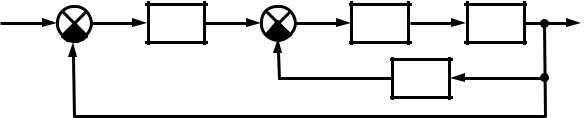
Таким образом, условие абсолютной устойчивости гармонически линеаризованной системы [1, 5, 7]:
∆n−1(q) > 0, при 0 ≤ q(A)≤ ∞ |
(12.3) |
где q(A) – коэффициент гармонической линеаризации нелинейного элемента.
Граница этой области устойчивости определяется как совокупность параметров л нейной части системы, при которой в нуль обра-
щается значен е определителя |
n−1(q), а его наименьшее значение име- |
|||||||
ет характер м н мума |
|
[1, 5, 7]. В результате получаем: |
||||||
функции |
|
|
|
|
|
|||
С |
∆n−1(q) = 0; |
|
||||||
|
|
|
|
|
|
(q) |
|
(12.4) |
|
|
|
∂∆ |
n−1 |
= 0. |
|||
|
|
|
|
|
|
|
||
|
|
|
|
∂q |
|
|
||
|
|
|
|
|
|
|
||
|
области |
|
||||||
Исключ в |
з эт х двух уравнений величину q(A), можно найти |
|||||||
границу |
|
солютной устойчивости, |
которая будет зависеть |
|||||
только от параметров |
нейной части системы [1, 5, 7]. |
|||||||
Пример. Дана структурная схема системы (рис. 12.1). Определим взаимосвязь параметров линейной части системы, обеспечивающую абсолютную устойчивость системы с нелинейным элементом F(x), обладающим однозначной нечётно-симметричной нелинейностью.
u(t) |
|
x |
z |
ЛЧ2 |
y(t) |
|
ЛЧА1 НЭ |
|
|||
– |
– |
|
|
|
|
|
|
|
ОС |
|
|
|
|
Д |
|
||
Рис. 12.1. Структурная схема нелинейной системы управления
Модель системы задана передаточными функциями:
WЛЧ1 |
= |
K1 |
|
; |
|
И(12.5) |
|||
(T1 p +1) |
|
||||||||
|
|
|
|
|
|
|
|||
WЛЧ 2 |
= |
|
K2 |
|
; |
(12.6) |
|||
(T2 p +1) p |
|||||||||
|
|
|
|
|
|||||
WОС ( p) = KOC . |
|
|
(12.7) |
||||||
82
Определим передаточную функцию части системы, замкнутой местной отрицательной обратной связью с коэффициентом KOC:
|
|
|
|
|
|
|
|
|
|
K2 |
|
F (x) |
|
|
|
|
|
|
|
|
K2 F (x) |
|
|
|
|
||||||||||||
|
W |
(р)= |
|
|
|
|
(T p +1) p |
|
|
|
|
|
|
|
|
|
|
. |
(12.8) |
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
K2 KOC |
|
|
|
|
|
|
|
|
(T p +1) p + K K F (x) |
|||||||||||||||||||||
МОС WЗАМ (p)= |
F |
|
(x) |
|
|
|
2 |
|
|
|
|
|
|
|
= |
OC |
|
|
|
||||||||||||||||||
|
|
|
|
1 |
+ |
(T p +1) p |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определ м передаточную функцию всей замкнутой системы: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K1 |
|
WМОС |
(p) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T p +1) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
K1 |
|
WМОС (p) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T p +1) |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
K1K2 F |
(x) |
|
|
|
|
|
|
|
F (x) |
. |
|
(12.9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
K |
|
|
F(x) |
|
+ K K |
|
|
|
|
||||||||
и(T p +1) T p + p + K |
2 |
ОС |
) |
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
( 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
Зап шем характеристическое уравнение гармонически линеари- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|||||||||||||||||||||||
зованной системы, т.е. при |
F(x) = q(A)x |
|
|
|
(A)(KОС + K1 )= 0 . |
(12.10) |
|||||||||||||||||||||||||||||||
T1T2 p |
3 |
+(T1 |
+T2 ) p |
2 |
+(1+ q(A)T1K2 KОС )р+ K2q |
||||||||||||||||||||||||||||||||
|
На границе устойчивости согласно формуле (12.4), имеем |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||||
|
|
|
∆n−1(q) =T1 +T2 +q(A)T1K2 |
(T1KОС |
−T2 K1 )= 0; |
|
|||||||||||||||||||||||||||||||
|
|
|
∂∆n−1(q) =T K |
2 |
(T K |
ОС |
−T K )= 0. |
|
|
|
|
|
. |
|
(12.11) |
||||||||||||||||||||||
|
|
|
|
∂q |
|
1 |
|
1 |
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Параметр, характеризующий нелинейную зависимость q(A), не |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||
вошёл в последнее уравнение. Границу абсолютной устойчивости оп- |
|||||||||||||||||||||||||||||||||||||
ределяем по параметрам линейной части системы (рис. 12.2) |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1KОС =T2 K1 . |
|
|
|
|
|
|
|
|
|
(12.12) |
|||||||||||||
|
Дополнительно необходимо проверить положительность ос- |
||||||||||||||||||||||||||||||||||||
тальных определителей Гурвица. Для системы третьего порядка по- |
|||||||||||||||||||||||||||||||||||||
ложительность остальных определителей (∆1 |
и ∆2) сводится к поло- |
||||||||||||||||||||||||||||||||||||
жительности коэффициентов характеристического уравнения. |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T +T > 0; |
|
|
|
|
|
|
|
|
|
|
(12.13) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KOC > −K1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
83
Таким образом, нелинейная АСУ с одной однозначной нечётносимметричной будет абсолютно устойчивой при следующем соотношении параметров линейной части системы:
С |
|
|
T K |
1 ; |
|
|
|
|
|
||
KОС |
> 2 |
|
|
|
|
(12.14) |
|||||
|
|
T1 |
|
|
|
|
|
|
|||
K |
OC |
> −K . |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
сти |
|
KОС |
K1 |
|
|||||||
|
0 |
|
|
|
|||||||
Область |
|
|
|
|
|
|
|
|
|
|
|
устойч во |
|
|
|
|
|
|
|
|
|
|
|
K = −K |
|
|
|
|
KОС = |
T2K1 |
|
|
|
||
|
|
|
|
T1 |
|
|
|||||
абсо |
|
|
|
|
|||||||
|
ОС |
1 |
|
|
|
|
|
|
|
|
|
Р с. 12.2. Граница и о ласть |
|
лютной устойчивости |
|
||||||||
|
|
А |
|
||||||||
Исходные данные для выполнения работы |
|
||||||||||
Заданная структурная схема модели нелинейной системы управления представлена на рис. 8.2 лабД. работы № 8. В табл. 12.1 пре д- ставлены характеристики и уравнения линейной и нелинейной частей нелинейной системы управления.
Требуется определить границы абсолютной устойчивости, кото-
1.Заменить нелинейную характеристикуИнелинейности F(x) коэффициентом гармонической линеаризации q(A).
2.Согласно исходным данным записать передаточную функцию гармонически линеаризованной замкнутой системы.
3.Определить характеристическое уравнение гармонически линеаризованной системы.
4.Вывести условия абсолютной устойчивости системы (12.4).
5.Записать и построить границы абсолютной устойчивости, за- висящие от параметров линейной части системы.рые будут зависеть от параметров линейной части системы.
84
Таблица 12.1
Параметры линейной и нелинейной частей системы
№ п/п |
Нелинейная часть |
Линейная часть |
С |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
–b |
|
|
|
WЛЧ (р)= |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
||||
0 |
b |
X |
|
(T1 p +1)(T2 p +1) p |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
||||
2 |
–b |
|
|
|
WЛЧ (р)= |
(T1 p +1)(T2 p +1) p + KKОС |
|||||||||||||||||
|
и0 b |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
А |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
K |
1 |
|
|
|
|||||
3 |
–b |
|
|
|
WЛЧ ( p) = |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
b |
|
|
(T12 p2 |
+T2 p +1) |
p |
|||||||||||||||||
|
|
|
0 |
|
ДK |
||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
И |
||||||||||||||||
|
|
B |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
–b |
|
|
|
|
WЛЧ ( |
р)= |
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
b |
X |
|
|
(Tp +1)2 p |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
–b |
|
|
|
|
WЛЧ ( |
р)= |
|
K(T1 p +1) |
|
|||||||||||||
|
|
|
|
(T p + |
1)2 p |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
0 |
b |
X |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85
|
|
Содержание отчета |
1. |
Название и цель работы. |
|
2. |
труктурная схема модели, передаточная функция линейной |
|
части и нелинейная характеристика нелинейной части системы. |
||
С |
|
|
3. |
Расчётные формулы и производимые по работе вычисления, |
|
в том числе система условия абсолютной устойчивости системы. |
||
4. |
Выражения и графики границы абсолютной устойчивости |
|
системы управлен я. |
|
|
5. |
Выводы по работе. |
|
задания |
||
Вопросы |
для защиты лабораторной работы |
|
1. |
Определен е устойчивости системы и её математическая ин- |
|
терпретац я. |
|
|
2. |
Что такое передаточная функция системы? |
|
3. |
Какбнайти характеристическое уравнение системы? |
|
4.Назов те т пы корней характеристического уравнения.
5.Как по критерию Гурвица можно определить наличие пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы?
6.Поясните методику определения границ абсолютной устойчивости системы.
7.Как по характеристическому уравнению гармонически линеаризованной системы составить матрицу Гурвица?
8.Назовите два условия определения границ абсолютной устойчивости системы. Д
И
86
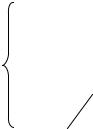
Лабораторная работа № 13
Анализ качества регулирования одноконтурной нелинейной системы по диаграммам качества
Цель работы − изучить метод анализа качества регулирования нелинейных автоматических систем управления с помощью диаграмм
качества. |
|
|
Общие сведения |
Эти |
|
СКолебательные переходные процессы нелинейных системах в |
|
первом пр бл жен |
могут ыть описаны затухающей или расходя- |
щейся с нусо дой с показателем затухания ζ и частотой колебаний ω. |
|
б |
|
процессы могут |
ыть затухающими до нуля или до амплитуды ав- |
токолебан й расходящимися изнутри до амплитуды автоколебаний |
|
или же расходящ м ся неограниченно в случае неустойчивости системы. Пр чем в отл ч е от линейных систем, показатель затухания колебаний ζ и частота ω системы во время переходного процесса не являются постоянными величинами, а меняются с течением времени [1, 5, 7].
Поэтому выражение для амплитуды колебаний А(t) следует определять в виде дифференциальной зависимости [1, 5, 7]
t |
|
|
|
|
∫ζdt |
|
dA |
|
|
A(t)= A e0 |
или |
= Aζ, |
(13.1) |
|
А0 |
|
|||
|
|
dt |
|
|
где A0 – начальное значение амплитуды колебаний, определяемое начальными условиями.
Текущее значение частоты колебаний ω в переходном режиме |
||
для нелинейных систем имеет видД |
|
|
ω = dϕ |
t |
|
или ϕ(t)= ∫ωdt +ϕ0 . |
(13.2) |
|
dt |
0 |
|
Таким образом, симметричный колебательный переходный про- |
|
цесс в нелинейных автоматических системах Инаходим в виде [1, 5, 7] |
|
y = Аsin ϕ; |
|
dA = Aζ; |
(13.3) |
dt |
|
ω = dϕ |
. |
dt |
|
87
Искомыми неизвестными здесь являются показатель затухания ζ, амплитуда А и частота колебаний ω. Причем при положительном значении показателя затухания ζ колебания расходятся до амплитуды автоколебаний или бесконечности, а при ζ < 0 колебания сходятся до нуля или до амплитуды автоколебаний.
В связи с этим формулы гармонической линеаризации при исследовании переходных процессов имеют некоторую особенность по сравнению с формулами для исследования автоколебаний. Выраже-
ние сигнала на входе нелинейной функции z = F(x) [1, 5, 7] |
|
||||||
и |
|
|
|
′ |
|
||
|
′ |
p −ζ |
|
′ |
ζ |
q (A) |
|
z = q(A)x |
+q (A) |
ω |
x = q(A) −q (A) |
x + |
ω |
px . (13.4) |
|
С |
|
|
|
ω |
|
||
В данном случае коэффициенты гармонической линеаризации |
||||||
q(A) q'(A) сохраняют свой вид для конкретной симметричной нели- |
||||||
б |
|
|
|
|
||
нейности могут ыть определены по табл. П.4. |
|
|
||||
Гармон ческая передаточная функция (ГПФ) |
нелинейного эле- |
|||||
мента в данном случае удет [1, 5, 7] |
|
|
|
|
||
А |
|
|
||||
WНЭ ( p) = |
z( p) |
= q(A) |
′ |
p −ζ |
. |
(13.5) |
|
x( p) |
|
|
ω |
|
|
В случае автоматической системы (см. рис. 8.2 лаб. работы № 8) с одной нелинейностью F(x) и передаточной функцией линейной час-
ти, обладающей свойством фильтра низких частот, |
|
WЛЧ (p)= R(p). |
(13.6) |
Q(p) |
|
Уравнения свободного движения замкнутой системы при вход- |
|
ном воздействии u(t) = 0 в операторной форме: |
|
Д |
|
Q(p)y = R(p)z; |
(13.7) |
|
|
z = F(x) = −F( y), |
|
или И
Q(p)y = −R(p)F(y). (13.8)
После гармонической линеаризации нелинейного элемента, согласно формуле (13.4), его уравнение в операторной форме имеет вид
|
′ |
p −ζ |
|
|
|
|
y . |
(13.9) |
|
z = − q(A) +q (A) |
ω |
|||
|
|
|
|
|
88
Тогда уравнение замкнутой системы (13.8) с учетом выражения (13.9) в операторной форме примет вид
|
|
′ |
p −ζ |
у = 0. |
(13.10) |
|
|
|
|
|
|||
Q (p)+ R(p) q(A) +q (A) |
ω |
|||||
|
|
|
|
|
|
|
Запишем характеристическое уравнение гармонически линеари-
зованной системы |
|
|
|
|
|
|
|
Q (p)+ R(p) |
|
′ |
|
p −ζ |
|
||
|
|
|
|
= 0 . |
(13.11) |
||
q(A) +q (A) |
ω |
|
|||||
|
|
|
|
|
|
|
|
Затухающ й ли расходящийся |
колебательный |
переходный |
|||||
С |
|
|
|
|
|
|
|
процесс (13.3) в нел нейной системе, описываемой уравнением |
|||||||
(13.10), соответствует паре комплексных корней p1,2 = ζ ± jω характе- |
|||||||
б |
|
|
|
|
|
||
ристического уравнен я (13.11). Поэтому для отыскания этого реше- |
|||||||
ния перейдем в частотную о ласть, заменив оператор p = ζ + jω. По- |
|||||||
лучимхарактер ст ческое уравнение в частотной форме [1, 5, 7] |
|||||||
Q (ζ+ jω)+ R(ζ+ jω)(q(A) + jq (A))= 0. |
(13.12) |
||||||
|
|
|
|
|
′ |
|
|
В комплексном уравнении (13.12) содержатся три неизвестных: ζ, ω и A, последняя из которых входит в коэффициенты гармонической линеаризации q(A) и q'(A).
Для отыскания решения уравнения (13.12) при высокой степени |
||||||||||||||||||
полинома подстановку p = ζ + jω целесообразно осуществлять путем |
||||||||||||||||||
разложения в ряд по Астепеням jω [1, 5, 7]. |
n d nQ |
|
||||||||||||||||
dQ |
|
1 |
|
|
2 |
d 2Q |
|
1 |
|
|
|
|||||||
Q(ζ+ jω)=Q(ζ)+ jω |
|
|
+ |
|
|
( jω) |
|
|
|
2 |
... + |
|
|
( jω) |
|
|
n |
,(13.13) |
dp |
2! |
|
dp |
n! |
dp |
|||||||||||||
|
ζ |
|
|
|
|
|
ζ |
|
|
|
ζ |
|||||||
где индекс «ζ» означает, что в выраженияДпроизводных надо подста- |
||||||||||||||||||
вить показатель затухания ζ вместо оператора Лапласа р. По такой же |
||||||||||||||||||
формуле разлагается в ряд и многочлен R(ζ + jω). |
|
|
|
|
|
|||||||||||||
Подставив полученный разложением в ряд многочлен в харак- |
||||||||||||||||||
теристическое уравнение (3.43), можно выделить его вещественную и |
||||||||||||||||||
мнимую части, что дает два уравнения [1, 5, 7]:И |
||||||||||||||||||
|
|
|
U (ζ, A,ω)= 0; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13.14) |
|
|
|
V (ζ, A,ω)= 0. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данная система позволяет найти две неизвестные переменные как функцию третьей – ζ(A) и ω(A) или ω(ζ) [1, 5, 7].
89

При анализе колебательного переходного процесса исследование может проводиться с точки зрения оценки влияния какого-либо параметра, например, KЛЧ – общего коэффициента усиления линейной части системы, на показатель затухания ζ и частоту колебаний ω. Это достигается построением так называемых диаграмм качества затухания
Ссимметричных нелинейных колебаний [1, 5, 7].
Диаграмма качества представляет собой семейства линий равного затухания ζ = const и линий равного значения частоты колебаний ω = const (р с. 13.1) показывает, как изменяются быстрота затухания пе-
реходного процесса частота колебаний системы при изменении ам- лебанийплитуды колебан й. Одной из координат всегда является амплитуда ко- А, другой – параметр системы, например, KЛЧ, подбирая кото-
рый можно получ ть нео ходимое качество переходного процесса.
А |
ζ < 0 |
ζ > 0 |
А |
ω = const |
|
|
ζ = 0 |
|
ω = 0 |
|
б |
|||
|
|
|||
А |
KЛЧ |
|
KГР KЛЧ |
|
|
|
Д |
|
Рис. 13.1. Диаграммы качества затухания симметричных нелинейных колебаний
В нелинейных системах, в отличии от линейных, линии равного затухания ζ = const искривляются или просто наклоняются в зависимости от формы нелинейности и общей структурыИсистемы. Это вы-
ражает собой изменение показателя затухания ζ и частоты ω нелинейных колебательных переходных процессов с изменением величины амплитуды колебаний А [1, 5, 7].
Особое значение имеют две линии: ζ = 0 и ω = 0. ζ = 0 соответс т- вует периодическому решению, а по линии ω = 0 можно ориентировочно оценивать границу между монотонными и колебательными переходными процессами в области устойчивости нелинейной системы.
Если линии ζ > 0 расположены ниже, чем ζ = 0, а ζ < 0 – выше, то периодическое решение устойчиво, т. е. оно соответствует автоколебаниям. Тогда линия ζ = 0 непосредственно дает нам зависимость амплитуды автоколебаний А от параметра KЛЧ. Кроме того, с помо-
90
щью линии ζ = 0 в этом случае опреде ляется колебательная граница устойчивости KГР нелинейной системы по параметру KЛЧ.
Левее значения KГР на рис. 13.1 будет область абсолютной устойчивости, так как переходные процессы затухают (ζ < 0) при любом начальном отклонении, причем дается количественная оценка быст-
СПравее значен я KГР лежит область неустойчивых колебаний, т.е. все колебательные процессы сходятся (если начальная точка на прямой KЛЧ(А) леж т выше линии ζ = 0) или расходятся (если начальная точка на прямой KЛЧ(А) лежит ниже линии ζ = 0), стремясь к усавтоколе ательному режиму. В первом случае амплитуда колебан й А уменьшается, а во втором – увеличивается (см. рис. 13.1). Если же н ζ > 0 расположены выше, чем ζ = 0, а ζ < 0 – ни-
роты затухания (величина ζ). По величине ω можно оценить при этом и число колебаний за время затухания переходного процесса от заданной начальной до заданной конечной амплитуды.
тельныйколебательнойпроцесс может перейти к другому устойчивому колебатель- а перерегулировани характеризуется средним значением переходного
же, то пер од ческое решение неустойчиво. |
|
тойчивому |
|
В |
нелинейной системе один устойчивый колеба- |
ному процессу. Тогда время регулирования отмеряет интервал времени между двумя соседними устойчивыми колебательными режимами,
колебательного процесса, которое определяется средним значением
амплитуды и частоты во время t = 0,5tP. |
|
|||||||
|
|
|
Д |
|||||
Длительность переходного процесса может определяться по |
||||||||
среднему значению ζАср на всем интервале изменения амплитуды коле- |
||||||||
баний (от А0 до А1) [1, 5, 7]. Тогда |
|
|
|
|
|
|||
t |
Р |
= |
1 |
ln |
A1 |
. |
(13.15) |
|
ζ |
|
|
||||||
|
|
ср |
|
A |
|
|||
|
|
|
|
0 |
|
|
||
Величину перерегулирования δ при начальной амплитуде коле-
баний А0 |
и среднем их значении в переходном режиме Аср можно оп- |
||||||
ределить, используя средние значения частоты ωсp и показателя зату- |
|||||||
хания колебаний ζср во время t = 0,5tP [1, 5, 7]: |
|
||||||
|
|
A |
π |
ζср |
И |
||
|
|
ω |
|||||
|
δ = |
ср |
100% |
= e |
ср 100% . |
(13.16) |
|
|
|
||||||
|
|
A |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Таким образом, используя вышеприведенные показатели качества, можно с достаточной степенью точности количественно оценить качество регулирования нелинейной автоматической системы в переходном режиме.
91
Рассмотрим анализ качества регулирования одноконтурной нелинейной системы (см. рис. 8.2 лаб. работы № 8) с типовой нелинейной характеристикой F(x) «Идеальное трехпозиционное реле» (см. табл. П.3, п. 7). Коэффициент усиления линейной части системы KЛЧ подлежит исследованию.
Уравнения свободного движения замкнутой системы при вход- |
|||
С |
|
|
|
ном воздействии u(t) = 0 в операторной форме |
|
||
|
(T1 p +1)(T2 p +1) py = KЛЧ z ; |
(13.17) |
|
|
z = F(x) = F(−y) = −F( y) ; |
(13.18) |
|
гдегармоническойкоэфф ц ент |
линеаризации q(A) определяется со- |
||
или |
(T1 p +1)(T2 p +1) py = −KЛЧ F (y). |
(13.19) |
|
После |
ческой линеаризации нелинейного |
элемента |
|
«Идеальное трехпоз ц онное реле» имеем |
|
||
б |
(13.20) |
||
|
z = −q(A)y , |
||
гласно табл. П.4, а коэффициент q'(A) = 0.
Зап шем характеристическое уравнение гармонически линеари- |
||||||||||||||||||||||||||||||
зованной системы |
А |
|
|
|
|
|
||||||||||||||||||||||||
|
T1T2 p |
3 |
+ |
(T1 |
+T2 ) p |
2 |
+ p + KЛЧ q(A)= 0 . |
|
|
(13.21) |
||||||||||||||||||||
Перейдем в частотную о ласть, заменив оператор p = ζ + jω: |
||||||||||||||||||||||||||||||
T T |
(ζ+ jω)3 +(T +T ) |
(ζ+ jω)2 +(ζ+ jω)+ K |
ЛЧ |
q(A)= 0. |
(13.22) |
|||||||||||||||||||||||||
1 2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Осуществим, согласно (13.13), разложение характеристического |
||||||||||||||||||||||||||||||
полинома D(ζ + jω) в ряд по степеням jω. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
dD |
|
1 |
|
|
|
|
2 d 2 D |
|
|
1 |
|
|
|
|
3 d3D |
|
||||||||||||
D(ζ+ jω)= D(ζ)+ jω |
|
|
|
|
+ |
|
|
( |
jω) |
|
|
|
|
2 |
|
+ |
|
И |
||||||||||||
dp |
2! |
|
dp |
|
3! |
( |
jω) |
|
dp |
3 ; |
(13.23) |
|||||||||||||||||||
|
|
|
ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Дζ ζ |
|||||||||||||||||||||
|
D(ζ)=T T ζ3 +(T +T )ζ2 +ζ+ K |
ЛЧ |
q(A); |
|
|
(13.24) |
||||||||||||||||||||||||
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dD |
|
= 3T T |
ζ2 + |
2(T |
|
+T )ζ+1; |
|
|
|
|
(13.25) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 d 2 D |
= |
3T T ζ+ |
(T |
+T ); |
|
|
|
|
|
(13.26) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2! dp2 |
ζ |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 d3D |
|
=T T . |
|
|
|
|
|
|
|
|
|
|
(13.27) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3! dp3 |
ζ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
92
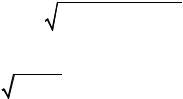
Выделим действительную часть характеристического полинома U(ζ, A, ω) и мнимую часть V(ζ, A, ω):
|
|
ζ |
3 |
+(T1 |
+T2 )ζ |
2 |
+ζ+ KЛЧ q(A)−(3T1T2ζ+(T1 |
2 |
|
||||||
T1T2 |
|
|
+T2 ))ω = 0; |
(13.28) |
|||||||||||
|
|
|
|
|
2(T +T )ζω+ω−T T ω3 = 0. |
|
|
||||||||
3T T ζ2ω+ |
|
|
|
||||||||||||
С |
|
|
2 |
|
1 |
2 |
|
|
|
|
|||||
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|||
|
Выделим величину ω из уравнения мнимой части V(ζ, A, ω). |
||||||||||||||
|
|
|
|
|
|
|
|
2 |
3T T ζ2 |
+2(T +T )ζ+1 |
|
|
|
||
|
|
|
|
|
|
ω = |
1 2 |
|
1 2 |
|
. |
|
(13.29) |
||
|
|
|
|
|
|
|
|
T1T2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
от коэфф ц ента ус ления линейной части системы KЛЧ, а зависит только от показателя затухания колебаний ζ и постоянных времени
частиКак в дно з формулы (13.29), частота колебаний ω не зависит
линейной |
|
|
с стемы T1 и T2. |
|
|
|
|
|
|
|
Полученное выражение (13.29) для ω2 подставляем в уравнение |
||||||||||
вещественной |
U(ζ, A, ω) и из него уравнения выделяем коэффи- |
|||||||||
циент ус лен я л нейной части системы |
|
|
|
|||||||
K |
|
= |
(3T1T2ζ+(T1 +T2 ))(3T1T2ζ2 |
+2(T1 +T2 )ζ+1) |
− |
|||||
|
|
|
|
|
|
|
|
|||
|
бq(A)T T |
|
|
|
||||||
|
ЛЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
(13.30) |
|
|
|
T T ζ3 + |
(T |
+T )ζ2 |
+ζ |
|
|||
|
|
|
. |
|
||||||
|
|
|
− 1 2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
q(A) |
|
|
|
|
|
|
Пусть параметрыАсистемы имеют следующие численные значе- |
||||||||||
ния: выходная величина реле B = 100; порог срабатывания реле b = 1; постоянные времени T1 = 0,05; T2 = 0,2.
С учетом этого выражения (13.29) и (13.30) приобретают вид |
|||||||||
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
2 |
|
|
|
ω(ζ)= 3ζД+50ζ+100 ; (13.31) |
||||||||
KЛЧ (A,ζ)= |
|
π |
A2 |
|
|
|
(0,021ζ3 |
+2ζ2 +15,25ζ+25). (13.32) |
|
|
|
|
|
|
|
||||
2 |
−1 |
||||||||
400 |
|
A |
|
|
|
||||
Уравнение (13.31) будет иметь решения при нахождении показателя затухания колебаний в областях –14,3426 ≥ ζ ≥ –2,3241. При ζ = 0 величина ω = 10 рад/с, в этой точке наблюдаются автоколебания, к которым стремится выходная величина системы.
Согласно зависимости KЛЧ(А, ζ) (13.32), рассчитаем значения коэффициента усиления линейной части системы KЛЧ для значений показателя затухания колебаний –14,3426 ≥ ζ ≥ –2,3241 (табл. 13.1).
93
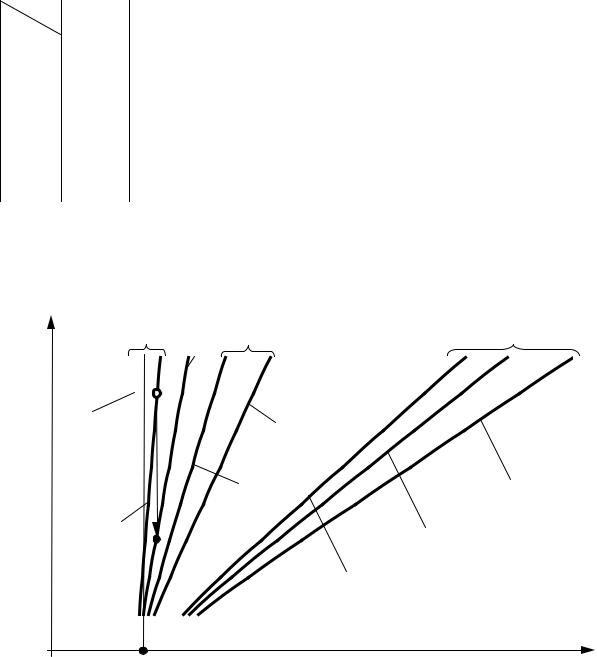
Таблица 13.1
Значения коэффициента усиления линейной части системы
|
A |
ζ |
–16,0 |
|
|
–15,0 |
–14,343 |
|
–2,324 |
|
–1,0 |
|
0,0 |
|
1,0 |
2,0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2,0 |
|
|
3,754 |
|
3,181 |
2,825 |
|
0,002 |
|
0,213 |
|
|
0,453 |
|
0,767 |
1,155 |
|
||||||||
|
4,0 |
|
|
6,716 |
|
5,690 |
5,053 |
|
0,003 |
|
0,381 |
|
|
0,811 |
|
1,372 |
2,066 |
|
||||||||
|
6,0 |
|
|
9,892 |
|
8,382 |
7,443 |
|
0,005 |
|
0,561 |
|
|
1,195 |
|
2,020 |
3,043 |
|
||||||||
|
8,0 |
|
|
13,108 |
|
11,106 |
9,863 |
|
0,006 |
|
0,743 |
|
|
1,583 |
|
2,677 |
4,032 |
|
||||||||
|
10,0 |
|
|
16,338 |
|
13,843 |
12,293 |
|
0,008 |
|
0,926 |
|
|
1,973 |
|
3,337 |
5,026 |
|
||||||||
|
значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
12,0 |
|
|
19,576 |
16,586 |
14,729 |
|
0,009 |
|
1,109 |
|
|
2,364 |
|
3,998 |
6,022 |
|
|||||||||
|
14,0 |
|
|
22,817 |
19,333 |
17,168 |
|
0,011 |
|
1,293 |
|
|
2,756 |
|
4,660 |
7,019 |
|
|||||||||
|
16,0 |
|
|
26,061 |
22,081 |
19,609 |
|
0,012 |
|
1,477 |
|
|
3,148 |
|
5,322 |
8,016 |
|
|||||||||
|
|
На д аграмме качества системы управления (рис. 13.2) отобра- |
||||||||||||||||||||||||
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
жены л н равных значений показателя затухания ζ, которым соот- |
|||||||||||||||||||||||||
|
ветствуют равные |
|
|
|
частоты колебаний ω. |
|
|
|
|
|
|
|||||||||||||||
|
А |
|
|
|
|
|
|
|
ζ = 0; |
ζ > 0 |
|
|
|
|
|
|
|
|
ζ < 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
ζ < 0 ω = 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16,0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
14,56=ω2;= |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
=ω–2,324;= |
|
|
|
|
|
|
|
12,37 |
|
|
|
|
|
|
|
|
|
|
|
|||
14,0 |
|
|
|
|
|
0 |
А |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
12,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
10,0 |
|
|
ζ = 7,28 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8,0 |
|
|
|
|
|
|
|
|
1; ω = |
ζ |
|
|
|
ζ = –16; ω = 8,24 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ω |
|
|
1 |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6,0 |
|
|
|
–1; |
|
|
|
|
ζ |
|
|
|
ζ = –15; ω = 5 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||
4,0 |
|
|
|
ζ= |
|
|
|
|
|
|
|
|
Д |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζ = –14,343; ω = 0 |
|
|
|
|
|
|
|
|||||
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0,0 KГР |
|
|
|
|
|
|
|
|
|
|
|
|
|
25,0KЛЧ |
||||||||
-5,0 |
|
|
5,0 |
|
|
10,0 |
|
15,0 |
|
20,0 |
||||||||||||||||
Рис. 13.2. Диаграммы качества колебательных переходных процессов одноконтурной нелинейной системы
Так как нелинейная характеристика системы однозначная, то линии KЛЧ(А, ζ) и KЛЧ(А, ω) будут совпадать.
94
На основании расчетов и построенной диаграммы качества можно сделать следующие выводы о динамических свойствах системы:
1) |
частота колебаний ω в переходном режиме для каждого зна- |
чения ζ постоянна и не зависит от коэффициента KЛЧ и амплитуды А; |
|
2) |
при заданных параметрах реле и постоянных времени линей- |
С |
|
ной части система имеет один устойчивый автоколебательный режим |
|
работы (линия ζ = 0) с частотой колебания ω = 10 рад/с; |
|
3) |
по линии ζ = 0 на диаграмме определяется колебательная |
граница устойч вости нелинейной системы по параметру KЛЧ. Левее |
||
значен я KГР = 0,453 на рис. 13.2 будет область абсолютной устойчи- |
||
при |
||
вости (устойч вость «в целом»), так как переходные процессы зату- |
||
хают (ζ < 0) |
лю ом начальном отклонении; |
|
4) |
правее значен я KГР = 0,453 лежит область автоколебаний, |
|
т.е. все |
|
процессы сходятся или расходятся, стремясь к |
|
колебательные |
|
устойч вому автоколе ательному режиму (к линии ζ = 0); |
||
5) |
л |
с показателем затухания ζ ≤ –14,3426 лежат ниже ли- |
нии ζ = 0; это означает, что периодическое решение (линия ζ = 0) для данных значен й показателя затухания ζ и соответствующих им значений коэффициента KЛЧ удет неустойчиво;
6) левее линии ζ = –2,324 и ω = 0 на диаграмме качества лежит область монотонных переходных процессов, т.е. переходные процессы будут не коле ательными, а апериодическими.
Оценим качество регулирования нелинейной автоматической
системы в переходном режиме. |
|
|
|
||||
А |
|||||||
Приближенно длительность переходного процесса tP можно оп- |
|||||||
ределить по ср еднему значению ζср на всем интервале изменения ам- |
|||||||
плитуды колебаний (от А0 |
до |
1) (13.15). Например, начальная точка 0 |
|||||
имеет амплитуду А0 = 14 и ζ0 = –1, а конечная точка на линии ζ = 0 |
|||||||
– точка 1 – имеет амплитуду А0 =Д6 и ζ0 = 0 (см. рис. 13.2), тогда |
|||||||
ζср = (–1 + 0)/2 = –0,5; |
|||||||
t |
Р |
= |
|
1 |
ln |
6 |
=1,69 с. |
−0,5 |
|
||||||
|
|
14 |
|
||||
Величину перерегулирования можно определить по формуле |
|||||||
|
|
|
|
|
|
|
И |
(13.16), используя средние значения частоты ωсp и показателя затухания колебаний ζср во время t = 0,5tP.
ζср = –0,5;
ω0 = 7,28 рад/с; ω1 = 10 рад/с; ωсp = (7,28 + 10)/2 = 8,64 рад/с;
δ = eπ8,64−0,5 100% = 83,3% .
95
Исходные данные для выполнения работы
Заданная структурная схема модели нелинейной системы управления представлена на рис. 8.2 лаб. работы № 8. В табл. 13.2 пре д- ставлены характеристики и уравнения с параметрами линейной и не-
С |
|
|
|
линейной частей нелинейной системы управления. |
|||
Требуется проанализировать динамические свойства нелинейной |
|||
системы управления в зависимости от значений коэффициента усиле- |
|||
ния линейной части с стемы KЛЧ. |
|
||
движен |
|
||
|
|
Порядок выполнения работы |
|
1. |
огласно сходным данным составить уравнение свободного |
||
|
я замкнутой с стемы в операторной форме. |
||
2. |
б |
|
|
Зап сать характеристическое уравнение гармонически ли- |
|||
неаризованной замкнутой системы управления. |
|||
3. |
Зап сать характеристическое уравнение системы управления |
||
в частотной форме с учетом показателя затухания колебаний ζ. |
|||
4. |
|
А |
|
Выделить вещественную и мнимую части характеристиче- |
|||
ского уравнения системы управления в частотной форме. |
|||
5. |
Выявить зависимости ω(ζ) и KЛЧ( |
, ζ). |
|
6. |
Определить о ласть существования решений полученных урав- |
||
нений для значений показателя затухания ζ и амплитуды колебаний А. |
|||
|
|
Д |
|
7. |
Рассчитать значения границы устойчивости KГР нелинейной |
||
системы по параметру KЛЧ при ζ = 0 и минимальному значению ам- |
|||
плитуды колебаний А из условий гармонической линеаризации. |
|||
8. |
Вычислить частоту колебаний ω устойчивых автоколеба- |
||
тельных режимов работы при ζ = 0. |
И |
||
9. |
Рассчитать значения KЛЧ для нескольких значений показате- |
||
ля затухания колебаний ζ и амплитуды колебаний А, из диапазонов, |
|||
определенных в п. 6. |
|
||
10. Построить диаграмму качества системы управления. |
|||
11. |
Проанализировать расположение |
линий равного затухания |
|
ζ = const на диаграмме и выявить область абсолютной устойчивости (устойчивость «в целом»), область автоколебаний, область значений коэффициента KЛЧ, соответствующих неустойчивости системы, область монотонных переходных процессов.
12. Оценить качество регулирования нелинейной автоматической системы в переходном режиме по длительности переходного процесса и величине перерегулирования.
96

Таблица 13.2
Параметры линейной и нелинейной частей системы
№ п/п |
Нелинейная часть |
Линейная часть |
С |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+2 |
|
|
|
|
WЛЧ (р)= |
|
|
|
K |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ЛЧ |
|
||||||
|
|
0 |
|
X |
|
(0,2 p +1)(2 p +1) p |
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бZ |
|
|
|
K |
|
|
|
|
|
||||||
2 |
–0,1 |
|
|
|
|
|
WЛЧ (р)= |
|
(0,2 p +1)2 p |
||||||||
|
и0,1 |
X |
|
|
|
||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
А |
|
|
K |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
–0,5 |
|
|
|
|
WЛЧ (р)= |
|
|
ЛЧ |
|
|||||||
|
|
|
|
|
(0,2 p +1)2 p |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
0,5 |
X |
|
ДK |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
И |
|||||||||
|
|
+10 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
–1 |
|
|
|
|
|
WЛЧ (р) |
= |
|
ЛЧ |
|
||||||
|
0 |
1 |
|
X |
( p +1)2 p |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
5 |
–1 |
|
|
|
|
WЛЧ (р)= |
|
|
|
ЛЧ |
|||||||
0 |
1 |
|
|
(0,2 p +1)(2 p +1) p |
|||||||||||||
|
|
|
|
X |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
–0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
97
|
Содержание отчета |
1. |
Название и цель работы. |
2. |
труктурная схема модели, передаточная функция линейной |
части и нелинейная характеристика нелинейной части системы. |
|
С |
|
3. |
Расчётные формулы и производимые по работе вычисления, |
в том числе зависимости ω(ζ) и KЛЧ(А, ζ). |
|
4. |
Области нахождения показателя затухания колебаний и ам- |
плитуды колебан й. |
|
5. |
Значен я гран цы устойчивости KГР. |
Показатели |
|
6. |
Частоты устойчивых автоколебательных режимов. |
7. |
Табл ца рассч танных значений KЛЧ для нескольких значе- |
ний показателя затухан я коле аний ζ и амплитуды колебаний А. |
|
8. |
Д аграмм качества системы управления. |
9. |
б |
Анал з расположения линий равного затухания. |
|
10. |
качества регулирования. |
11. Выводы по анализу качества регулирования.
Вопросы и задания для защиты лабораторной работы
1.Перечислите основные показатели качества регулирования нелинейной автоматической системы.
2.Как определяется качество колебательных переходных процессов в нелинейных системах?
3.В чем особенность колебательных переходных процессов в нелинейных системах?
4.В каком виде ищется симметричный колебательный переходный процесс в нелинейных автоматических системах?
5.На что влияет показатель затухания колебаний ζ ?
6.Что такое диаграмма качества затухания симметричных нелинейных колебаний и как её построить?
7.Что определяется по линиям ζ = 0 и ω = 0 на диаграммах ка-
чества?
8.Как по диаграмме качества определяется колебательная граница устойчивости нелинейной системы?
9.Как по диаграмме качества определяется устойчивое и неустойчивое периодические решения?
10.Как определяется величина перерегулирования нелинейной автоматической системы при начальной амплитуде колебаний А0?АИ
98
Лабораторная работа № 14
Моделирование и синтез типовых нелинейных звеньев
Цель работы − изучить метод синтеза нелинейных характеристик для нелинейных автоматических систем управления.
Нел нейные характеристики можно классифицировать по опре- |
||||
симметр |
|
|||
деленности значен й выходной величины z в статическом стационар- |
||||
Сном реж ме [1, 5, 7]: |
|
|
||
• |
однозначные; |
|
||
• неоднозначные (многозначные). |
||||
|
б |
|||
Нел нейные характеристики могут иметь различные типы |
||||
|
[1, 5, 7]: |
|
|
|
• |
чётно-с мметричная характеристика; |
|||
• |
нечётно-с мметричная характеристика; |
|||
|
|
А |
||
• |
несимметричная характеристика. |
|||
По характеру зависимости выходной величины z от входной ве- |
||||
личины x нелинейные характеристики разделяются на [1, 5, 7]: |
||||
• |
гладкие; |
|
Д |
|
• |
ломаные; |
|
||
• |
кусочно-линейные. |
|||
|
||||
В ряде случаев для упрощения расчёта гладкую характеристику приближенно заменяют кусочно-линейной [1, 5, 7].
В табл. П.3 представлены статические характеристики и уравне- |
|
ния типовых нелинейностей, аппроксимированных кусочно-линейной |
|
или гладкой зависимостью. |
И |
|
|
Статическая характеристика нелинейной системы строится по статическим характеристикам составляющих её звеньев, исходя из их соединения, определяемого структурной схемой. Вначале по характеристикам отдельных звеньев строят характеристики групп последовательно и параллельно соединенных звеньев, а также звеньев, охваченных местными обратными связями [5].
Для последовательного соединения звеньев задаются рядом дискретных значений входной величины X. Для каждого из этих значений определяется соответствующее значение выходной величины каждого звена, являющегося входной величиной для следующего звена, и так до получения значения выходной величины всей цепочки Y.
99
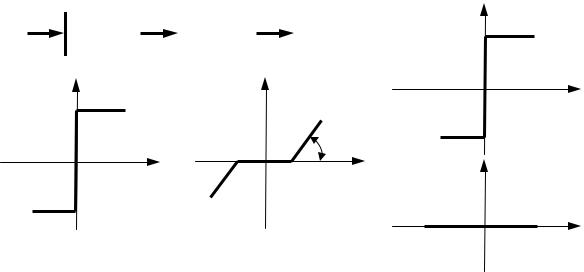
Рассмотрим пример последовательного соединения двух нелинейных элементов «Идеальное двухпозиционное реле» и «Зона нечувствительности», статические характеристики которых представлены в табл. П.3. В данном случае результирующая статическая характеристика Z2(X) может иметь два вида в зависимости от того, будет ли выходной сигнал первого нелинейного элемента – уровень срабатывания реле B больше порога зоны нечувствительности b (рис. 14.1).
x |
|
|
|
|
z1 |
|
|
|
z2 |
|
|
Z2 |
|
|
|
НЭ1 |
|
|
НЭ2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
k(B – b) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
С |
|
|
|
|
|
|
|
= |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
Z2 |
|
|
|
0 |
|
|||
|
|
|
|
|
|
при |B| > |b| |
|
X |
||||||
|
B |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
∙ |
–b |
|
arctg(k) |
|
–k(B – b) |
|
||
|
0 |
|
|
|
0 b |
|
Z1 |
Z2 |
|
|
||||
и |
|
|
|
|
|
|||||||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
–B |
|
|
|
|
|
|
|
= |
|
Z2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
X |
|
|
|
|
|
|
|
|
|
|
|
при |B| ≤ |b| |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
б |
|
|
|
|
|||||||
Рис. 14.1. Построение статической характеристики последовательного |
|
|||||||||||||
|
|
|
|
|
|
соединения нелинейных звеньев |
|
|
||||||
|
|
|
|
|
|
А |
|
|
||||||
|
При параллельном соединении звеньев ордината искомой зави- |
|||||||||||||
симости Y определяются как сумма ординат статических характери- |
||||||||||||||
стик отдельных звеньев [5]. |
|
|
|
|
|
|
||||||||
|
Рассмотрим пример параллельного соединения двух НЭ « де- |
|||||||||||||
альное двухпозиционное реле» и «Зона нечувствительности», стати- |
||||||||||||||
|
|
|
|
|
|
|
|
|
Д |
|
||||
ческие характеристики звеньев те же, что и в примере на рис. 14.1. В |
||||||||||||||
данном случае результирующая статическая характеристика Y(X) на- |
||||||||||||||
ходится путем сложения ординат звеньев НЭ1 и НЭ2 при ряде дис- |
||||||||||||||
кретных значений входной величины X (рис. 14.2). |
|
|
||||||||||||
|
Для коррекции статических характеристикИнелинейных звеньев |
|||||||||||||
иногда необходимо составить соединение со сложной смешанной |
||||||||||||||
структурой, содержащей и последовательное, и параллельное соедине- |
||||||||||||||
ния звеньев. Составление сложных соединений линейных и нелиней- |
||||||||||||||
ных характеристик может использоваться на этапе синтеза нелинейных АСУ для разработки модели нелинейного регулятора, управляющего технологическим объектом с нелинейной внутренней характеристикой.
100
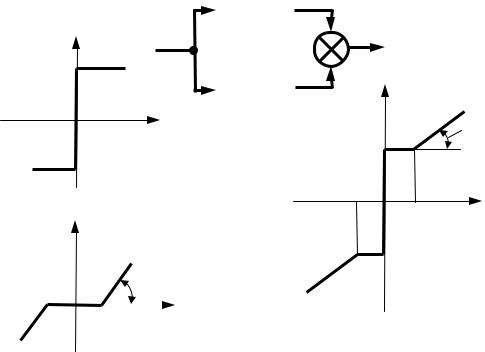
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
НЭ1 |
+ y |
|
|
|
|
|
|
|
|
|
|
|
||
Z1 |
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
B |
|
|
|
|
z2 |
+ |
|
|
|
|
|
|
НЭ2 |
|
|
|||
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
X |
|
|
B |
|
arctg(k) |
|
|
|
|
|
|
|
|
|||
|
|
–B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
= |
|
–b |
b |
|
|
|
|
|
|
0 |
X |
||||
Z2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
С |
|
|
|
|
–B |
|
|
||
|
|
|
|
|
|
|
|
|
|
–b |
|
|
arctg(k) |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
0 |
X |
|
|
|
|
|
||
и |
|
|
|
|
|
||||
Рис. 14.2. Построен |
е статической характеристики параллельного соединения |
||||||||
|
|
|
нелинейных звеньев |
|
|
||||
|
б |
|
|
|
|||||
|
|
|
А |
|
|
||||
Если в нелинейной системе имеются неизбежные, вредные для управления нелинейности (люфт, гистерезис, зона нечувствительности), то путем введения специальной нелинейной коррекции можно ослабить вредное влияние имеющихсяДв системе нелинейностей [5].
Пример. Естественная нелинейность в виде зоны нечувствительности (см. табл. П.3, п. 1) вносит дополнительные статические и динамические ошибки в работу системы. Поэтому необходимо компенсировать влияние такой нелинейности. Пусть нелинейное усилительное звено с функцией F1(x) имеет зонуИнечувствительности 2b. Для компенсации её влияния параллельно с заданным нелинейным звеном включают нелинейное звено с функцией F2(x) с таким же к о- эффициентом усиления в пределах от –b до +b без зоны нечувствительности, но с зоной насыщения после значения |b| (рис. 14.3).
Выходной сигнал y будет складываться из двух параллельных сигналов. В пределах зоны нечувствительности 2b входной сигнал будет проходить через нелинейное звено с функцией F2(x). После зоны нечувствительности характеристика F2(x) не изменяется (она в зоне насыщения), и сигнал будет проходить через звено F1(x). Таким образом, с помощью параллельных нелинейных характеристик получена одна общая линейная характеристика.
101
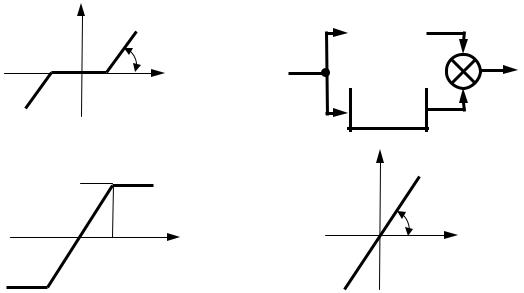
Z1 |
|
|
|
|
|
z1 |
|
|
|
|
F1(x) |
|
|||
|
|
arctg(k) |
|
+ |
|
||
–b |
b |
x |
|
y |
|||
|
|||||||
|
|
|
|
||||
0 |
X |
|
|
|
z2 + |
|
|
|
|
|
F2(x) |
|
|
||
|
|
|
|
|
|
|
|
+
Z2
B
–b |
|
|
|
arctg(k) |
С0 b |
X |
= |
0 |
X |
–B |
|
|
|
|
. 14.3. Компенсац |
я нелинейности в виде зоны нечувствительности |
|||
Рис |
|
|
|
|
б |
|
|
||
Главная трудность такой коррекции нелинейного звена F1(x) состоит в подборе второго нелинейного звена F2(x), у которого зона насыщен я коэфф цАент усиления совпадали бы с зоной нечувствительности и коэффициентом усиления функции F1(x).
Исходные данные для выполнения работы
В табл. 14.1 представленыДстатические характеристики нелинейностей, имеющихся в нелинейной системе управления.
Необходимо провести структурную коррекцию заданного нелинейного звена согласно требованиям к системе и смоделировать статические и динамические характеристики исходных и скорректиро-
1.Провести структурную коррекциюИзаданного нелинейного звена путем последовательного и/или параллельного сложения заданной нелинейной характеристики с типовыми характеристиками других типовых нелинейных звеньев.
2.Моделирование характеристик нелинейностей проводить в Simulink программного комплекса Matlab согласно схеме, представленной на рис. 14.4. Задание сигналов для получения характеристик производится с помощью блока Signal Builder (рис. 14.5).
102
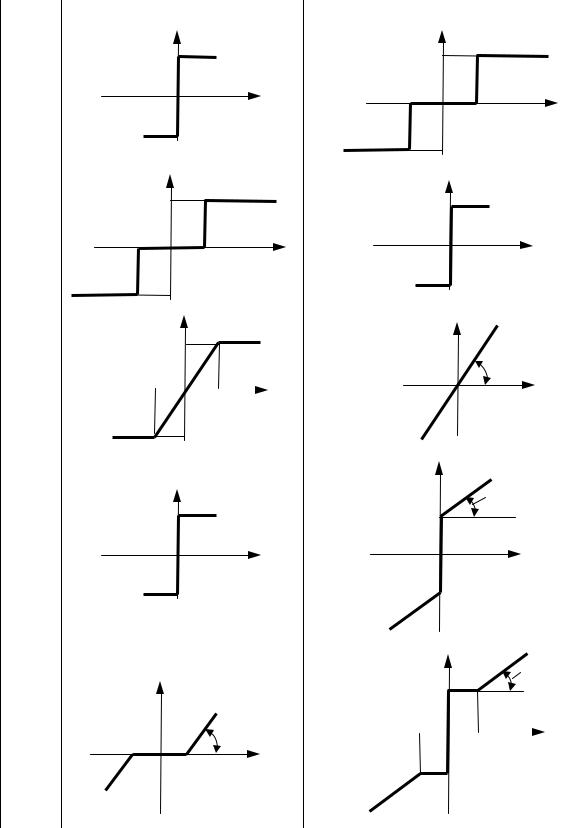
Таблица 14.1
Параметры нелинейностей нелинейной системы управления
|
№ п/п |
Заданная нелинейность |
|
Требуемая нелинейность |
|
||||||||||
|
|
Z |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
СZ |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
||
|
|
+2 |
|
|
|
|
|
+0,5 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
–0,01 |
|
|
|
|
|
|
|
||
|
|
|
|
–2 |
X |
|
|
0 |
0,01 |
|
X |
|
|||
|
и |
|
|
|
–3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
–0,5 |
|
|
|
|
|
||
|
|
+2 |
|
|
|
|
|
+3 |
|
|
|
|
|
|
|
2 |
–0,1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
0 |
0,1 |
|
|
|
X |
|
||||||||
|
|
|
X |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
А |
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
3 |
б–0,5 |
|
0 |
|
arctg2 |
|
|||||||||
|
|
|
|
0 |
0,5 X |
|
|
|
|
X |
|
||||
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Д |
||||||||
|
|
Z |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
+2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
4 |
Z |
0 |
|
|
|
И2 |
|
||||||||
|
|
|
X |
|
|
0 |
|
|
X |
|
|||||
|
|
|
|
|
|
|
–1 |
|
|||||||
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
–0,1 |
|
|
arctg3 |
|
–0,5 |
|
|
|
|
|
|
|
||
|
|
|
0 |
0,5 |
|
X |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 0,1 |
X |
|
|
|
|
|
|
||||||
|
|
|
|
–2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103
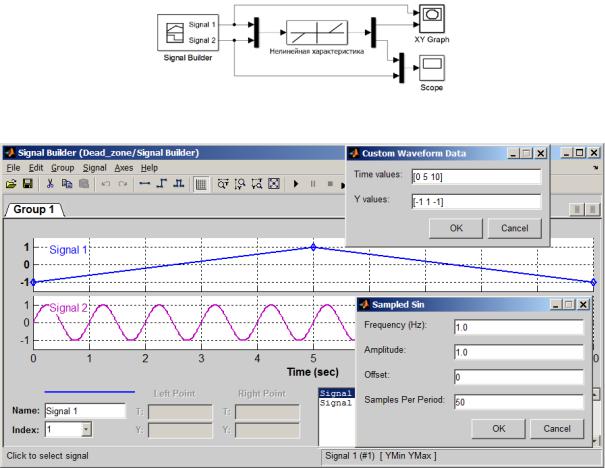
Рис. 14.4. Схема для исследования нелинейных характеристик Си б
Рис. 14.5. ВнешнийАвид настроек построителя сигналов «Signal Builder»
1.Название и цель работы.Д
2.Заданная нелинейная и скорректированная характеристики
системы, структурная схема с добавочными типовыми характеристиками типовых нелинейных звеньев. И
3.Статические и динамические характеристики исходных и скорректированных нелинейностей, полученные в XY Graph и Scope.
1.Приведите классификацию нелинейных характеристик.
2.В чем суть структурной коррекции нелинейных звеньев?
3.По указанию преподавателя нарисовать статическую характеристику и уравнение типового нелинейного звена.
4.Поясните методику расчета результирующей характеристики последовательного и параллельного соединения нелинейных звеньев.
104
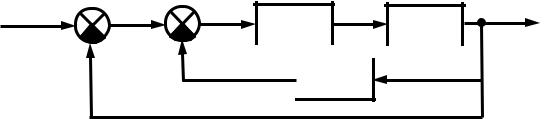
Лабораторная работа № 15
Исследование скользящего режима работы одноконтурной релейной системы управления
Цель работы − изучить метод синтеза и исследования скользящего режима работы нелинейных автоматических систем управления.
Общие сведения
жиме |
|
В релейной автоматической системе управления при отсутствии |
|
Сзоны нечувств тельности реле фазовый портрет будет иметь устойчи- |
|
вый фокус с предельным циклом установившихся колебаний. Для |
|
уменьшен я ампл туды установившихся колебаний, а в идеале для |
|
полной л кв дац |
коле ательного процесса в установившемся ре- |
дополн тельно в о ратную связь включают дифференцирующее |
|
звено для создан я г |
кой отрицательной обратной связи (ГОС). То- |
гда в такой нел нейной |
системе может возникнуть особый |
скользящий режим ра оты [1, 5, 7]. |
|
Для иллюстрациибра оты нелинейной автоматической системы |
|
управления в скользящем режиме рассмотрим структурную схему, |
|
представленную на рис. 15.1 |
при входном воздействии u(t) = 0. |
u(t) = 0 |
x |
z |
ЛЧ |
y |
|
АНЭ |
|
||
– |
y |
– |
y'KOC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ГОС |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Д |
||||||||
|
|
|
|
|
||||||||||
Рис. 15.1. Структурная схема нелинейной системы со скользящим режимом |
||||||||||||||
Уравнение линейной части ЛЧ системы имеет вид |
|
|||||||||||||
|
|
|
p2 y = Kz , |
|
|
|
|
|
(15.1) |
|||||
|
|
|
|
|
|
|
|
|
И |
|||||
а уравнение нелинейного элемента НЭ с характеристикой « |
деальное |
|||||||||||||
двухпозиционное реле» (см. табл. П.3, п. 6) описывается нелинейной |
||||||||||||||
функцией |
|
|
|
B при x1 > 0; |
|
|||||||||
|
|
z = F(x) = |
(15.2) |
|||||||||||
|
|
|
< 0. |
|
|
|
||||||||
|
|
|
|
−B при x1 |
|
|
|
|
||||||
105
Местная гибкая отрицательная обратная связь описывается передаточной функцией [1, 5, 7]
|
|
WГОС ( p) = KОС p . |
|
|
|
|
(15.3) |
|||||||||
Общее дифференциальное уравнение свободного движения сис- |
||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
темы в операторной форме при u(t) = 0 будет иметь вид [1, 5, 7] |
|
|||||||||||||||
|
p2 y = −KF(y + pyKOC ) . |
|
|
|
(15.4) |
|||||||||||
Введем новые переменные состояния xi(t) вместо (i–1) произ- |
||||||||||||||||
водных выходной вел чины y(t): |
|
|
|
|
|
|
|
|
|
|
|
|||||
системы |
= y ; |
x2 = y . |
|
|
|
|
|
(15.5) |
||||||||
|
|
|
x1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получ м д фференциальное уравнение фазовых траекторий |
||||||||||||||||
[1, 5, 7] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
= − |
|
F(x + x K |
OC |
). |
|
|
|
(15.6) |
||||||
|
|
|
|
x2 |
1 |
|
|
2 |
|
|
|
|
|
|||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Л н я переключения на фазовой плоскости [x1; x2] |
на рис. 15.2 |
|||||||||||||||
|
А |
|
|
|||||||||||||
описывается уравнен ем [1, 5, 7] |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x1 + x2KОС = 0. |
|
|
|
|
|
(15.7) |
|||||||
В связи с релейной функцией НЭ на фазовой плоскости [x1; x2] |
||||||||||||||||
можно выделить две области: (1) |
где F(x1 |
+ x2KОС) = +B и (2) где |
||||||||||||||
F(x1 + x2KОС) = –B. |
|
|
|
|
Д |
|
||||||||||
Справа от линии переключения при (x1 + x2KОС) > 0 функция |
||||||||||||||||
F(x1 + x2KОС) = +B и уравнение фазовых траекторий имеет вид |
|
|||||||||||||||
|
x2 = −2KBx + x2 |
+2KBx . |
|
(15.8) |
||||||||||||
|
2 |
|
|
1 |
20 |
|
|
|
|
10 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
Слева от линии переключения при (x1 |
+ x2KОС) < 0 функция |
|||||||||||||||
F(x1 + x2KОС) = –B и уравнение фазовых траекторий имеет вид |
|
|||||||||||||||
|
x2 = 2KBx + x2 |
|
−2KBx . |
|
|
(15.9) |
||||||||||
|
2 |
|
|
1 |
20 |
|
|
|
|
10 |
|
|
|
|
||
Найдем закон движения в скользящем процессе. На линии пере- |
||||||||||||||||
ключения имеет место уравнение [1, 5, 7] |
|
|
|
|
|
|
||||||||||
|
x + x K |
OC |
= 0 или y + dy K |
OC |
= 0 . |
(15.10) |
||||||||||
|
1 2 |
|
|
|
|
|
|
|
dt |
|
|
|
|
|||
Решением данного уравнения является выражение [1, 5, 7] |
|
|||||||||||||||
|
|
|
y(t) = y e |
− |
t |
|
|
|
|
|
|
|
|
|||
|
|
|
Koc , |
|
|
|
|
(15.11) |
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
106
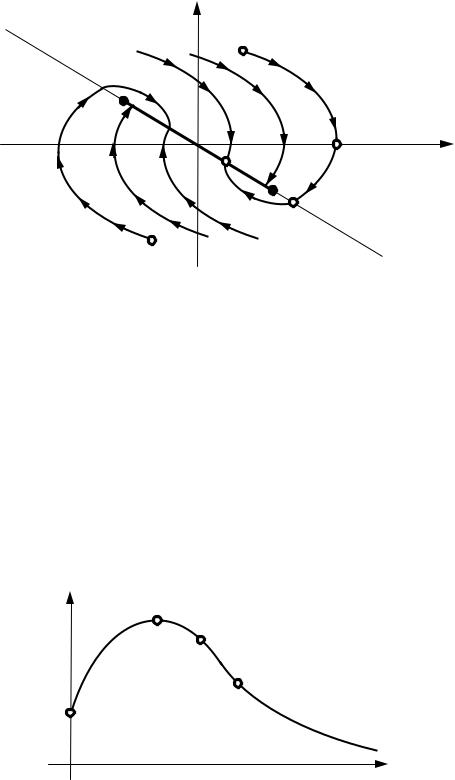
где значения t = 0 и y = y0 считаются в момент попадания изображающей точки на линию скользящего процесса. Итак, скользящий процесс происходит по экспоненциальному закону [1, 5, 7].
С |
x2 |
= y |
|
|
|
|
|
|
M01 |
|
|
||
|
|
|
|
|||
|
|
|
|
B |
(1) |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
и |
|
|
|
M11 |
||
0 |
M31 |
|
|
x1 = y |
||
|
|
|
|
|||
(2) |
|
|
|
|
M21 |
|
б |
|
x1 + x2 KOC = 0 |
||||
|
|
|||||
|
|
|
||||
|
M02 |
|
|
|
|
|
Р с. 15.2. Фазовый портрет нелинейной |
СУ в скользящем режиме |
|||||
А |
|
|||||
Нелинейная система второго порядка на участке скользящего |
||||||
процесса AB вырождается в линейную систему первого порядка, т.е. |
||||||
вначале был коле ательный процесс (до точки М31 |
рис. 15.2), а затем |
|||||
движение по линии переключения заканчивается практически апе- |
||||||
риодическим процессом. При этом |
закон движения в скользящем |
|||||
|
|
Д |
||||
процессе не зависит от параметров прямой цепи системы и определя- |
||||||
ется только коэффициентом обратной связи. Например, при началь- |
||||||
ном положении М01 |
(см. рис. 15.2) получим фазовую траекторию |
|||||
М01М11М21М31, переходящую в скольжение в точке М31. Такой фазовой |
||||||
траектории соответствует процесс во времени y(t), изображенный на |
||||||
|
|
|
|
|
И |
|
рис. 15.3, где отмечены характерные точки [1, 5, 7]. |
|
|||||
y |
|
M11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M21 |
M31 |
|
|
|
|
|
|
|
|
||
M01 |
|
|
|
|
|
|
0 |
|
|
|
|
|
t |
Рис. 4.13. Переходный процесс системы на линии переключения
107
Найдем положение концов отрезка скользящего процесса А и В на фазовой плоскости (см. рис. 15.2). Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие согласно формуле (15.6) можно записать в виде [1, 5, 7]
|
|
|
|
|
|
|
А |
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
x2 |
= − |
|
, |
|
|
(15.12) |
|||||||
|
|
|
|
|
|
|
А |
|
|
|
|
|
|||||||
|
|
|
|
|
|
x1 |
|
|
|
KOC |
|
|
|
||||||
тогда из уравнения фазовых траекторий (15.6), подставив условие |
|||||||||||||||||||
(15.8), получ м для точек А и В выражение [1, 5, 7] |
|
||||||||||||||||||
− |
1 |
= − |
K |
F(x |
|
+ K |
OC |
x |
) = − KB ; |
(15.13) |
|||||||||
|
|
|
|
||||||||||||||||
С |
KOC |
|
|
x2 А |
|
1А |
|
|
|
2 А |
x2 А |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2 А = KBKOC и |
x1А = −x2 АKOC ; |
(15.14) |
|||||||||||||||||
|
|
||||||||||||||||||
− |
|
1 |
= − |
K |
F(x |
+ K |
|
|
x |
) = + KB . |
(15.15) |
||||||||
|
KOC |
|
|
|
|||||||||||||||
|
|
|
|
x2B |
|
1B |
|
|
|
OC |
2B |
x2B |
|
||||||
и |
|
|
|
|
|
|
|
|
|
(15.16) |
|||||||||
|
|
x2B = −KBKOC и x1B = −x2B KOC . |
|||||||||||||||||
Следовательноб, отрезок скользящего процесса АВ тем больше, чем больше коэффициентыАусиления прямой цепи и обратной связи.
Скользящий режим в системе с дифференцирующим звеном в цепи обратной связи возникает не при любом значении KОС. Для его возникновения наклон фазовой траектории после переключения реле должен быть больше, чем наклон линии переключения. Но возможен случай, когда скользящий режим возникнет не сразу, а на втором или на третьем, или на n-ном витке устойчивого фокуса [1, 5, 7].
Для установления апериодического процесса изменения выходной координаты нелинейной системы управления на первом же витке
фазовой траектории необходимо, |
чтобы |
изображающая |
точка при |
|
|
|
|
И |
|
первом же переключении реле попалаДна отрезок скользящего про- |
||||
цесса АВ, т.е. |
|
|
|
|
для области (1) и точки B: |
x1 ≤ x1B |
при x2 = x2B . |
(15.17) |
|
и области (2) и точки А: |
x1 ≥ x1A |
при x2 |
= x2 A . |
(15.18) |
При симметричной характеристике реле достаточно выполнения любого из условий. Тогда после линии переключения фазовая траектория остается на линии переключения.
Найдем, согласно (15.17) и уравнению фазовых траекторий (15.8), ограничение для коэффициента усиления ГОС из требования наискорейшего установления апериодического процесса на первом же витке фазовой траектории.
108
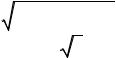
|
x |
|
x2 |
− x2 |
−2KBx |
|
||||||||||||
Из (15.8) выразим |
= |
2 |
|
|
|
|
20 |
|
|
|
|
10 |
|
; |
(15.19) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
−2KB |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
из (15.16) и (15.17) получим x2 = x2B = −KBKOC |
(15.20) |
|||||||||||||||||
x |
= −x |
|
|
K |
OC |
= KBK 2 . |
(15.21) |
|||||||||||
|
1B |
|
|
2B |
|
|
|
|
|
ОС |
|
|||||||
В итоге неравенство (15.17) представляем в виде |
|
|||||||||||||||||
KBKОС2 |
≥ |
(−KBK |
OC |
)2 − x2 |
−2KBx |
(15.22) |
||||||||||||
|
|
|
|
|
|
|
20 |
10 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
−2KB |
|
|
|
|
|
|||
После преобразований и выделения коэффициента усиления |
||||||||||||||||||
ГОСполуч м огран чение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x2 |
|
+2KBx |
|
|||||||||
|
KOC ≥ |
|
|
|
|
20 |
|
|
|
|
10 |
. |
(15.23) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
KB 3 |
|||||||||||||
Привыполнен этого условия изображающая точка фазовой |
||||||||||||||||||
траектори при первом же переключении реле попадает на отрезок |
||||||||||||||||||
скользящего процесса |
остается на нем. Как видно из формулы зна- |
|||||||||||||||||
чение коэффициента усиления ГОС зависит не только от параметров |
||||||||||||||||||
б |
|
|
|
|
|
|||||||||||||
системы, но и от начальных отклонений переменных состояния сис- |
||||||||||||||||||
темы (положения начальнойАточки фазовой траектории M0.)
Однако при чрезмерном увеличении коэффициента усиления ГОС увеличивается перерегулированиеДи длительность переходного процесса системы управления.
Учитывая вышеизложенное, можно синтезировать скользящий режим работы релейной системы управления.
Исходные данные для выполненияИработы
Заданная структурная схема модели нелинейной системы управления представлена на рис. 15.1. В табл. 15.1 представлены характеристики и уравнения с параметрами линейной и нелинейной частей нелинейной системы управления, а также максимально возможные начальные отклонения переменных состояния системы в виде положения начальной точки фазовой траектории M0.
Требуется синтезировать скользящий режим работы релейной системы управления, исходя из требований наискорейшего установления апериодического процесса, минимального перерегулирования и длительности переходного процесса системы управления.
109
Таблица 15.1
Параметры линейной и нелинейной частей системы
№ вар. |
Нелинейная часть |
Линейная часть |
Начальные условия |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(р)= 1,5 |
М0_мах(2; 2); |
||||||||
|
|
|
|
|
|
W |
|
|||||||||||
1 |
|
|
|
|
|
|
ЛЧ |
|
|
|
|
р2 |
М0_мах(4; 0); |
|||||
|
|
|
0 |
X |
|
|
|
|
|
|
|
|
М0_мах(4; 4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
5 |
|
|
М0_мах(1; 1); |
||||||||||
2 |
|
|
|
W |
|
(р)= |
(2 |
р +1)р |
М |
(5; 0); |
|
|||||||
|
и |
|
ЛЧ |
|
|
|
М00__махмах(5; 5) |
|||||||||||
|
|
|
0 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
А |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
М0_мах(3; 3); |
||
|
|
|
|
|
|
WЛЧ (р)= |
2 |
|
|
|||||||||
3 |
–0,5 |
|
|
|
|
|
М |
(5; 0); |
|
|||||||||
|
|
|
р2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0_мах |
|||||
|
|
0 |
0,5 |
X |
Д2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
М0 мах(5; 5) |
|||||
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
И |
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
WЛЧ (р)= |
|
|
|
|
|
|
М0 мах(1; 1); |
||||||
4 |
|
|
|
(1 |
р+1)р |
М0 мах(5; 0); |
||||||||||||
|
|
|
0 |
X |
|
|
|
|
|
|
|
|
|
|
|
М0 мах(6; 1) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
М0_мах(3; 3); |
||
|
|
|
|
|
WЛЧ (р)= |
|
|
3 |
|
|
||||||||
5 |
–0,5 |
|
|
|
|
|
|
|
|
М0_мах(5; 0); |
||||||||
|
|
(3 |
р+1)р |
|||||||||||||||
|
|
0,5 |
X |
|
|
|
|
|
М0_мах(5; 5) |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
110
Порядок выполнения работы
1. Согласно математическому описанию (табл. 15.1) и струк-
турной схеме системы (см. рис. 15.1) получить дифференциальное |
|
уравнение фазовых траекторий системы в скользящем режиме. |
|
С |
|
2. |
Найти уравнение линии переключения |
3. |
Найти решения дифференциального уравнения фазовых тра- |
екторий x2 = f(x1) для различных областей фазовой плоскости с учетом начальных условий.
4. Найти огран чение для коэффициента усиления гибкой оттеристрицательной обратной связи с учётом максимально возможных начальных отклонен й переменных состояния системы.
5. Получ ть фазовый портрет и переходные временные харакки с стемы в скользящем режиме с заданными начальными
условиями.б
Содержание отчета
1.Название и цель ра оты.
2.Структурная схема модели, передаточная функция линейной части и нелинейная характеристика нелинейной части системы.
3.Расчётные формулы, дифференциальное уравнения фазовых траекторий системы, ограничение для коэффициента усиления ГОС.
4.Значения коэффициента усиления гибкой отрицательной обратной связи при различных начальных отклонениях системы.
5.Фазовый портрет и переходные временные характеристики системы в скользящем режиме с заданными начальными условиями.АД
Вопросы и задания для защиты лабораторной работы
1.Что такое фазовая траектория и фазовый портрет?
2.Поясните процесс получения параметрического и дифференциального уравнений фазовых траекторий системы.
3.Как реализуется скользящий режим работы в нелинейных автоматических системах?
4.Что называется скользящим процессом в нелинейных автоматических системах?
5.Как меняется линия переключения реле на фазовой плоскости в скользящем режиме?
6.От каких параметров зависит отрезок скользящего процесса?И
111
