
- •Введение
- •1.1. Теоретическая часть работы
- •1.2. Экспериментальная часть работы
- •1.3. Порядок выполнения экспериментальной части лабораторной работы
- •1.4. Порядок выполнения экспериментальной части работы на автоматизированной установке
- •Контрольные вопросы и задания
- •2.1. Анализ исходной задачи испытания
- •2.2. Постановка задачи. Выбор критерия сбора данных
- •2.3. Физический эксперимент
- •2.4. Последовательность выполнения работы
- •2.5. Обработка результатов испытаний
- •2.7. Численный эксперимент
- •2.8. Анализ результатов
- •Контрольные вопросы
- •3.1. Краткие теоретические сведения
- •3.3. Порядок проведения работы и обработка результатов испытаний
- •3.4. Оценка результатов работы
- •Контрольные вопросы
- •4.1.Краткие теоретические сведения
- •4.2. Экспериментальное определение динамических характеристик колебаний балки с распределенной массой
- •4.3. Порядок проведения работы и обработка результатов испытаний
- •4.4. Оценка результатов работы
- •Контрольные вопросы
- •Библиографический список
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный автомобильно-дорожный университет (СибАДИ)»
СИБАДИИЗМЕРЕНИЕ УПРУГИХ И РЕЛАКСАЦИОННЫХ СВОЙСТВ МАТЕРИАЛОВ СТРОИТЕЛЬНЫХ КОНСТРУКЦ Й
ДИНАМИЧЕСКИМ МЕТОДОМ
Методические указания к лабораторным работам
Составители: П. . Самосудов, В.Г. Тютнева
Омск - 2017

УДК 69.058 (075.8) ББК 38.74
И37
Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, причиняющей вред их здоровью и развитию» данная продукция маркировке не подлежит.
Рецензент
канд.техн.наук, доц. А.Р. Нелепов (ООО ТПИ «Омскгражданпроект»)
СИБАДИРабота утверждена редакционно-издательским советом СибАДИ в качестве методических указаний.
Измерение упругих и релаксационных свойств материалов строительных И37 конструкций динамическим методом : методические указания к лаборатор-
ным работам [Электронный ресурс] / сост : П.А. Самосудов, В.Г. Тютнева. –
Электрон.дан. – Омск : СибАДИ, 2017. - URL: http://bek.sibadi.org/cgi-bin/
irbis64r plus/cgiirbis 64 ft.exe. - Режим доступа: для авторизованных пользователей.
Предназначены для проведения лабораторных работ и самостоятельной подготовки одного из сложнейших разделов строительных конструкций « инамика и устойчивость зданий и сооружений». В основе лабораторных работ лежит наиболее распространенный в инженерной практике метод экспериментального определения основных динамических характеристик элементов конструкций по собственной частоте основного тона колебаний. Данные указания освещают основные аспекты лабораторного практикума: теоретическое обоснование, используемые установки и приборы, методики проведения работы и обработки экспериментальных данных, вопросы для самоконтроля.
Адресованы обучающимся по направлениям подготовки: 08.05.01 «Строительство уникальных зданий и сооружений», 08.04.01 «Теория и проектирование зданий и сооружений» и при дипломном проектировании.
Работа подготовлена на кафедре «Строительные конструкции».
Текстовое (символьное) издание ( 5 МБ)
Системные требования: Intel, 3,4 GHz; 150 МБ; Windows XP/Vista/7; DVD-ROM; 1 ГБ свободного места на жестком диске; программа для чтения pdf-файлов: Adobe Acrobat Reader; Foxit Reader
Редактор И.Г. Кузнецова Техническая подготовка Н.В. Кенжалинова
Издание первое. Дата подписания к использованию 02.10.17
Издательско-полиграфический комплекс СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПК СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1
ФГБОУ ВО «СибАДИ», 2017
Введение
В методических указаниях даны описание испытательных стендов, моделей конструкций и порядок проведения лабораторных работ по измерению упругих и релаксационных свойств материалов строительных конструкций динамическим методом.
Активный физический эксперимент предусматривает последова- СИБАДИтельное или поэтапное совершенствование модели конструкций с целью достижения желаемого НДС. Для этого в модели заранее выбираются регулируемые параметры, задаются или определяются области их измене-
ний (ограничений) и ставятся цели, которые необходимо достигнуть. Выделяются два направления в проведении активного эксперимента,
которые укладываются в методику поэтапного изменения модели: последовательное преобразование различных элементов в виде постановки связей и т. п. и последовательное их ослабление.
Поиск новых оригинальных эффективных способов регулирования динамических характеристик и способов обеспечения устойчивости строительных систем составляет суть инженерного искусства. Инженерное осмысление результатов физического эксперимента может подтолкнуть к новым конструктивным решениям, особенно при активной форме эксперимента.
3
Лабораторная работа №1
ЗАКОНОМЕРНОСТИ УПРУГОГО ПОВЕДЕНИЯ МАТЕРИАЛОВ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ, ПОДВЕРЖЕННЫХ ДИНАМИЧЕСКИМ НАГРУЗКАМ
Цель работы: ознакомиться с особенностями упругих свойств мате- СИБАДИриалов и экспериментальными методами определения физикомеханических характеристик свойств материалов динамическим методом.
Приборы и оборудование: компьютерные осциллограф, частотомер, задающий генератор, испытательные стенды, образцы материалов строительных конструкций.
1.1. Теоретическая часть работы
Строительные конструкции уникальных зданий и сооружений из металлов и композитов в процессе эксплуатации в условиях внешних нагрузок и напряжений сохраняют свои размеры и форму, т.е. обладают достаточной жесткостью. Это обусловлено упругими свойствами металлов и сплавов. Следовательно, упругие свойства материалов в значительной степени определяют эксплуатационную надежность и работоспособность зданий и сооружений и широко используются в практике инженерных расчетов на прочность и устойчивость.
Упругость – это свойство тел изменять форму и размеры под воздействием внешних нагрузок и самопроизвольно восстанавливать исходную конфигурацию при прекращении внешнего воздействия. Для большинства металлов и сплавов упругость проявляется в области малых деформаций ~ 1%. Взаимосвязь между величиной упругой деформации и величиной внешних напряжений определяется характеристиками (модулями) упругости, которые являются физическими константами материала и зависят от его природы.
Физическая природа упругих свойств обусловлена силами взаимодействия атомов в кристаллической решетке металлов и сплавов. В исходном состоянии, когда внешние усилия отсутствуют, атомы занимают равновесные положения в узлах кристаллической решетки. В этом состоянии сумма всех сил, действующих на каждый атом со стороны окружающих, равна нулю, а потенциальная энергия атома – минимальная. Под воздействием внешних сил (напряжений) атомы смещаются из равновесных положений, при этом величина смещения определяется силами межатомных связей. После снятия внешних нагрузок конфигурация и размеры упругого тела восстанавливаются. Причиной этого является самопроизвольное (за
4
счет внутренних сил межатомного взаимодействия) возвращение атомов из неравновесного, неустойчивого положения в исходное, равновесное.
Закономерности упругого поведения металлов были впервые изучены Гуком в 1678 г. Он установил, что при одноосном растяжении взаимосвязь между напряжением δ и величиной упругой деформации ε имеет линейный характер:
Е . |
(1.1) |
СИБАДИ |
|
Коэффициент пропорциональности |
Е называется модулем нормаль- |
ной упругости или модулем Юнга и определяется углом наклона прямой 0 – 1 к горизонтальной оси на начальном участке диаграммы растяжения (рис. 1.1). Модуль нормальной упругости не зависит от знака деформации, его величина при растяжении и сжатии одинакова.
В случае действия касательных напряжений τ, вызывающих сдвиго-
вую упругую деформацию εсд, закон Гука имеет вид |
|
G сд , |
(1.2) |
где G – модуль сдвига или модуль упругости при сдвиге. |
|
Отношение модуля сдвига G к модулю Юнга Е для металлов с различными типами кристаллической решётки является величиной постоянной и составляет G/E ≈ 0,375.
При всестороннем (гидростатическом) сжатии или растяжении, когда исходный (начальный) объём V0 тела изменяется на величину V, закон Гука выражается линейной пропорциональностью между гидростати-
ческим давлением Р и относительным изменением объёма χ = |
V/V0: |
Р k , |
(1.3) |
где k – модуль объёмной упругости.
Соотношения (1.1), (1.2), (1.3) представляют собой элементарный закон Гука, когда напряжения и деформации действуют в одном и том же направлении.
При растяжении цилиндрического образца увеличение его длины – относительное удлинение δ = l/l – должно сопровождаться соответственным уменьшением его диаметра – относительным сужением ψ = α/α.
ледовательно, одноосное напряженное состояние приводит к возникновению трёхосной всесторонней деформации (см.рис. 1.1).
Отношение изменения размеров образца в поперечном направлении (диаметра) к изменению размеров в продольном направлении (длины) на-
зывается коэффициентом Пуассона ν: |
|
|
|
d / d . |
(1.4) |
|
l / l |
|
5

Рис. 1.1. Диаграмма деформации при растяжении:(0 – 1) – участок упругой деформации (Закон Гука); (1 – 2) – участок пластической деформации упрочнения
(образование «шейки»); (2 – 3) – участок пластической деформации разупрочнения; ε1 = εу – упругая обратимая деформация; ε2 – пластическая деформация, соответствующая пределу прочности σВ; ε3 – пластическая деформация, соответствующая моменту разрушения; ε = (ε3 + εу) – полная величина деформации разрушения;
Е = tgα – модуль упругости Юнга; D = tgβ – модуль пластичности
Величина коэффициента Пуассона ν одинакова при растяжении и сжатии. Для большинства металлов и сплавов ν находится в пределах
0,25…0,35.
Соотношения между рассмотренными константами упругости изотропных кристаллических материалов (металлов и сплавов) приведены в табл. 1.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
||||
|
|
Соотношения между модулями упругости изотропных тел |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
звестные ве- |
|
|
|
|
Определяемые величины |
|
|
|
|
|||||||||
|
личины |
|
E |
|
|
|
G |
|
|
k |
|
ν |
|
|
|
||||
|
k, G |
|
9kG |
|
|
|
|
|
|
|
|
|
|
|
4,5k |
|
|
1 |
|
|
|
(3k G) |
|
|
|
|
|
|
|
|
|
|
(3k G) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k, ν |
3k(1 2 ) |
3 |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k, E |
|
|
|
|
|
3kE |
|
|
|
1 |
|
E |
|
|||||
|
|
|
|
|
(9k E) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
6k |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
E |
|
|
E |
|
|
|
|
|
|||
|
E, ν |
СИБАДИ |
|
|
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2(1 ) |
3(1 |
2 ) |
|
|
|
|
|
|||||
6
E, G |
|
|
|
|
|
|
E |
|
|
E |
1 |
|
|
|
|
|
3(3G E) |
|
|
2G |
|||||
|
|
|
|
|
|
|
|
|
|
|||
G, ν |
4,5G(1 |
) |
|
3 |
|
1 |
|
|
|
|||
|
|
|
G |
|
|
|
|
|
||||
|
2 |
1 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
С кристаллографической точки зрения упругие свойства материалов
описываются компонентами матриц [коэффициентов упругости Cij или упругих податливостей Sij (i,j – направления кристаллографических осей)].
СИБАДИгде Cmn = Cijkl. Tm Cmn n , (1.6)
Для монокристаллических материалов взаимосвязь между напряжением и деформацией имеет ярко выраженный анизатропный характер, т. е. зависит от кристаллографического направления осей кристаллической решетки. Закон Гука для монокристаллов в обобщенном виде можно
представить следующей формулой:
Тij Cijkl kl . |
(1.5) |
Уравнение (1.5) означает, что деформация кристалла зависит не только от приложенного напряжения, но и от направления и вида приложенного напряжения. Напряженно-деформированное состояние монокри-
сталлов характеризуется тензором напряжений Tij и тензором. Взаимо-
связь между этими характеристиками определяется коэффициентами упругости Cijkl, которые по физическому смыслу являются модулями упругости по различным кристаллографическим осям. При этом если в поликристаллическом изотропном материале растягивающее напряжение вызывает только деформацию растяжения вдоль той же оси и поперечное сужение, то в монокристалле (анизотропном материале) это напряжение может вызвать растяжение, сжатие, сдвиг в любых направлениях в зависимости от того, какова кристаллографическая симметрия монокристалла.
Для трехосной системы каждая из компонент тензора kl связана с каждой компонентой тензора Tij соотношением
11 = C1111 T11 + S1112 T12 + S1113 T13 + S1121 T21+ S1122 T22 +
+ S1123 T23 + S1131 T31 + S1132 T32 + S1133 T33.
Всего имеется 9 таких уравнений, в каждое из них входит 9 коэффи-
циентов Sijkl, т. е. имеется 81 независимый компонент матрицы Sijkl.
В силу симметричности тензоров Tij и kl количество независимых
компонентов сокращается до 36. Вследствие симметрии кристаллов, т. е. симметричности ij и kl, уравнение (1.5) можно записать в виде
7
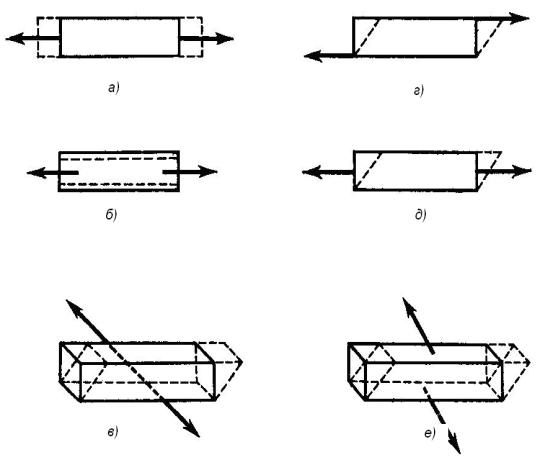
Таким образом, матрицу Cijkl можно представить в виде аналогичной ей матрице с двухиндексным обозначением Cmn, каждая из компонент тензора Cmn характеризует связь между определенными компонентами напряжений и деформаций. Физический смысл компонент коэффициентов упругости Cmn определяется характером взаимосвязи между действующим напряжением и деформацией. Это схематически дано на рис. 1.2, где
стрелками показано направление приложенного напряжения, а пунктиром СИБАДИ– вызванные ими деформации.
Компоненты С11, С22, С33 связывают нормальные (растягивающие или сжимающие) напряжения с параллельными им деформациями продольного удлинения по трем возможным направлениям (рис. 1.2, а).
Компоненты С12, С13, С23, С21, С31, С32 характеризуют связь между нормальным напряжением и деформацией поперечного сжатия (рис.1.2, б).
Рис. 1.2. Взаимосвязь коэффициентов упругости Сijkl со схемой напряженного состояния
Компоненты С44, С55, С66 связывают напряжения сдвига (касательные) с деформацией сдвига параллельно приложенному напряжению (рис. 1.2, в).
8
Компоненты С24, С26, С34, С35, С15, С16 связывают нормальные растягивающие напряжения с деформациями сдвига в плоскости, параллельной напряжению (рис. 1.2, г).
Компоненты С14, С25, С36, С41 связывают нормальные напряжения с
деформациями сдвига в плоскостях, параллельных приложенному напряжению, при этом направление сдвига перпендикулярно направлению напряжения (рис.1.2, д).
СИБАДИДля различных напряженно-деформированных состояний коэффициенты упругости лейкосапфира имеют следующие значения:
Компоненты С45, С46, С56, С54, С64 связывают напряжения сдвига с
деформациями сдвига в перпендикулярном направлении (рис. 1.2, е).
Матрица коэффициентов упругости гексагональной решетки (т. е.
сапфира) имеет следующую форму:
С11 |
С12 |
С13 |
С14 |
С15 |
С16 |
С21 |
С22 |
С23 |
С24 |
С25 |
С26 |
С31 |
С32 |
С33 |
С34 |
С35 |
С36 |
С41 |
С42 |
С43 |
С44 |
С45 |
С46 |
С51 |
С52 |
С53 |
С54 |
С55 |
С56 |
С61 |
С62 |
С63 |
С64 |
С65 |
С66 |
С11 = С22 = 496; С12 = 164; С13 = С23 = 115; С3 = 498; С44 = С55 = 148.
В инженерных расчетах используют модуль нормальной упругости (модуль Юнга) Е, модуль сдвига G, модуль объемной упругости k , а также коэффициент Пуассона ν. Эти характеристики имеют простой физический смысл, легко поддаются экспериментальному определению, взаимосвязь между ними представлена в табл. 1.1.
Экспериментальные методы определения модулей упругости можно разделить на две группы – статические и динамические. В первом случае модуль упругости определяют путем измерения упругой деформации, возникающей в образце при приложении известного постоянного напряжения. Прикладывая растягивающую нагрузку и измеряя удлинение, находят модуль нормальной упругости I рода или модуль Юнга. Для получения достаточно точных значений модуля упругости статическими методами необходимо проводить измерения деформаций в максимально широком интервале нагрузок. Это повышает вероятность выхода из области упругого поведения материалов. Недостатком статических методов является то, что для проведения испытаний требуются специальные об-
9
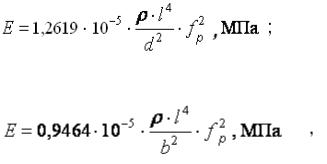
разцы, форма и размеры которых регламентируются ГОСТ 1497 – 73. Особые требования предъявляются к чистоте поверхности рабочей части образца.
Динамические методы определения упругих свойств позволяют производить измерения при малых деформациях и отличаются более высокой чувствительностью. Возможность применения динамических методов для измерения модулей упругости определяется высокой скоростью распро-
СИБАДИстранения упругой деформации в материалах.
Для динамического определения упругих свойств материалов разработано несколько методов. Наибольшее распространение получили:
- метод изгибных колебаний образца на резонансной и собственной частоте;
- метод крутильных колебаний; - импульсный метод по измерению скорости распространения упру-
гих волн.
Для определения модуля нормальной упругости Е по измерению частоты резонансных изгибных колебаний свободно подвешенного образца используются следующие формулы:
- для образца с круглым поперечным сечением
(1.7)
- для образца с квадратным, прямоугольным сечением
(1.8)
где ρ = m/V – плотность материала, кг/м3; l – длина образца, м; d – диаметр цилиндрического образца, м; b – размер квадратного сечения, м; fр – резонансная частота изгибных колебаний, Гц.
Оценка достоверности результатов измерений модулей нормальной упругости материалов динамическим методом может быть выполнена по ГО Ту [1].
Методика определения упругих свойств материала по измерению резонансной частоты свободно подвешенного образца позволяет одновременно определить релаксационные свойства материала, т. е. характеристики внутреннего трения.
Внутреннее трение – свойство металлов и сплавов необратимо рассеивать энергию механических колебаний. Рассеяние энергии колебаний обусловлено релаксационными процессами тепловой, атомной или магнитной перестройки в структуре материала, которые вызывают дополни-
10
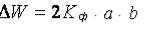
тельную деформацию упругого последействия. В зависимости от метода измерения внутреннее трение характеризуется различными показателями.
1. Относительное рассеяние энергии за цикл
W /W , |
(1.9) |
где W – потеря энергии за цикл; W – упругая энергия системы. |
|
СИБАДИфаз: |
|
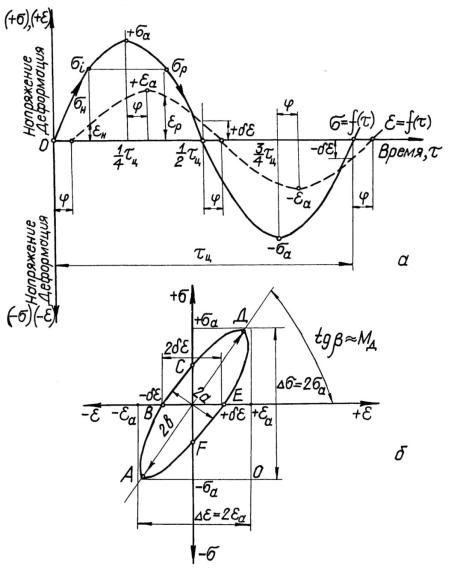
Анализ петли гистерезиса (рис.1.3,а) |
показывает, что энергия де- |
формации при нагружении Wн, соответствующая площади под кривой ABCD, больше энергии деформации при разгружении ; Wp – площадь под кривой DEFA. Таким образом, потеря энергии за один цикл составляет
W = Wн – Wр = Пл(ABCDOA) – Пл(DEFAOD)
и равна площади петли гистерезиса.
На практике при непосредственном построении (записи) петли гистерезиса в координатах σ – ε потеря энергии W рассчитывается по сле-
дующему выражению: |
|
|
(1.10) |
где Kф – коэффициент формы петли гистерезиса, Kф = 1,33…1,57; |
a, b – |
большая и малая полуоси петли гистерезиса. |
|
Полная упругая энергия за один цикл равна |
|
W a a , |
(1.11) |
где a – амплитуда напряжений; a – амплитуда деформаций. |
|
Принимая форму петли гистерезиса в виде эллипса, получаем сле-
дующие выражения для полуосей (рис. 1.3, б): |
|
||
a sin ; |
(1.12) |
||
2 |
|
|
|
b |
a |
. |
(1.13) |
|
|||
|
sin |
|
|
Учитывая синусоидальный характер изменения величины |
дефор- |
||
мации |
|
||
2 a sin , |
(1.14) |
||
после соответствующих подстановок и преобразований получаем соотношение между относительным рассеянием энергии за цикл и углом сдвига
2 sin . |
(1.15) |
11
Вследствие малости угла φ принимаем sinφ = tgφ, тогда
tg / 2 |
W |
. |
(1.16) |
|
|||
|
2W |
|
|
Рис. 1.3. зменение напряжения и деформации при циклическом нагружении упругопластичного тела:
а –диаграмма σ = f(τ); ε = f(τ); б – гистерезисная петля σ – ε
2. Внутреннее трение Q-1 по физическому смыслу обратно пропорционально механической добротности колебательной системы. Внутреннее трение с относительным рассеянием энергии взаимосвязано следующим образом:
Q 1 tg / 2 |
W |
. (1.17) |
|
||
|
2W |
|
СИБАДИ |
||
12
