1. Работа с двухмерными объектами

Итак, от простого к сложному. Для начала рассмотрим задачи, решаемые ПГП при построении двухмерных объектов. Общая концепция обработки информации представлена на рисунке 7.1.

Рис 1-1 Общая концепция обработки информации

Рассмотрим данную схему более подробно.

1. Примитивы вывода в мировых коорднатах

Ранее говорилось, что все изображения строятся на основе геометрических примитивов, описывающих реальный объект в м.к. (координатах пользователя). При выводе этих примитивов на экраносуществляется видовая операция.

2. Видовая операция

Под видовой операцией понимается процесс отображения окна в поле вывода в нормированных координатах. Видовая операция представляет собой совокупность операций отсечения по окну и отображения по окну в поле экрана в н.к.

Отсечение по окну

• Данная операция подразделяется на следующие этапы:

• отсечение точек;

• отчение отрезков.

Рассмотрим эти операции более подробно.тсечение точек

Данная операция довольно проста. Для того, чтобы отсечь какую-либо точку необходимо проверить её видимость. Для этого достаточно проверить следующие условия:

Xmin<=X<=Xmax, где X,Y- координаты точки;

Ymin<=Y<=Ymax.

Остальные значения - границы окна.

1. Отсечение отрезков

Далее необходимо отсечь отрезки.

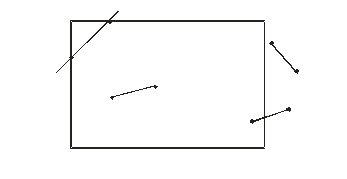
Рис. 1-2

Как видно из рисунка, все отрезки можно разделить на следующие группы:

• полностью лежащие внутри окна (a,b);

• не попадающие в окно (i. j);

• пересекающие границы окна.

Так как сложные изображения состоят из большого числа графических примитивов, то очевидно, что необходим алгоритм быстрого вычисления или сортировки отрезков по полной и неполной принадлежности к окну.

Сортировка

Для этого можно воспользоваться простым алгоритмом определения видимости. Для каждого отрезка: если одна из координат находится вне окна, то отрезок не полностью виден.

if Xa<Xл or Xa>Xп then go 1

if Xa<Xл or Xa>Xп then go 1

if Yа<Yн or Ya>Yв then go 1

if Yв<Yн or Yв>Yв then go 1

Отрезок полностью виден: вывод - go 3.

1. Проверка полной невидимости;

ifXa<XлandXв <Xлthen go2

ifXa<XпandXв >Xпthen go2

ifYa<YвandY >Yвthen go2

ifYa<YнandYв <Yвthen go2

Отрезок частично виден или пересекает продолжение границы оставаясь невидимым (i,j) : определить пересечение с окном.

2. Отрезок невиден;

3.Переход к следующему отрезку.

Формализация данного алгоритма для аппаратной реализации была осуществлена Коэном и Сазерлендом. Суть алгоритма заключается в том, что каждому концу отрезка приписывается код по следующей схеме.

Рис. 1-3

Таким образом, если коды обоих концов равны нулю, то отрезок виден полностью. Воспользовавшись логическим умножением имеем:

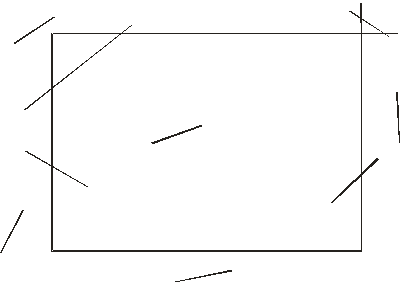
Рис. 1-4

П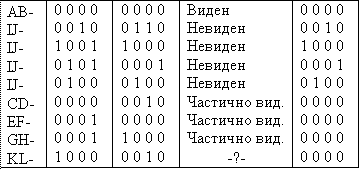

КL- пересечение с границами.

Пересечение отрезков с окном

Существуют два способа вычисления координат точек пересечения отрезков с окном:

• параметрический;

• непараметрический

Параметрический способ

Уравнение прямой, проходящей через точки (X1 Y1) и (X2Y2) имеет вид:

Y=M(X-X1)+Y1 или Y=M(X-X2)+Y2, где M=(Y2-Y1)/(X2-X1);

Точки пересечения определяются следующим образом:

Xл Y= M(Xл-X1)+Y1 , M

Xп Y= M(Xп-X1)+Y1 , M

Yв X= X1+(1/M)(Yв-Y1) , M0

Yн X= X1+(1/M)(Yн-Y1) , M0

На основе логических сравнений найденных координат можно осуществить разбиение отрезка на 2 или 3 и рассматривать их отдельно.

Рис. 1-4

Непараметрический способ

Непараметрический способ представляет собой алгоритм разбиения средней точкой (поисковый метод).

Рис. 1-5

Разбиение отрезка на 2 аппаратным способом- быстрая операция эквивалентная сдвигу битов вправо.

Пример:

6110 (двоичное).

Сдвиг вправо 1 1 0 0 1 1 3 (десятичное).

Суть алгоритма заключается в проверке каждой половины принадлежности окну и отбрасывании невидимой части.

Рис. 1-6