Параметрические кубические кривые

Для начала определим метод описания пространственных кривых.

Наиболее приемлем способ, при котором кривая описывается многочленом 3-й степени:

x(t)=axt+bxt+cxt+dx

y(t)=ayt+byt+cyt+dy

z(t)=azt+bzt+czt+dz

0<t<1 (переход от точки i к i+1 точке)

Кубические уравнения выбраны потому, что для сегментов произвольной кривой:

-не существует представление более низкого порядка, которая обеспечивает сопряжение на границах связи

-при более высоком порядке, появляются осцилляции и волнистость.

Из ряда способов описания бикубических кривых (метод Эрмита, метод Безье и т.п.) наиболее применяем метод В-сплайнов, для которого характерно несовпадение кривой с аппроксимируемыми точками что, однако гарантирует равенство 1-й и 2-й производных при стыковке сегментов.

Форма В-сплайнов наиболее гладкая. Терминсплайнпроисходит от названия длинных металлических линеечек, с помощью которых чертежники размечали поверхности кораблей, самолетов.

В-сплайн описывается следующей формулой:

x(t)=TMsGsx– обобщенная форма описания кривой для всех методов

Где: T=[t³,t²,t,1] – параметр, определяющий переход от точки Piк Pi +1

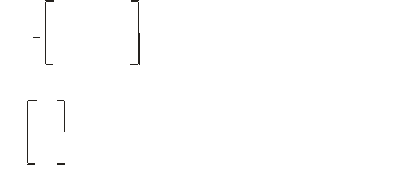
Геометрическая матрица для перехода от точки Piк Pi+1

Pi-1, Pi, Pi+1, Pi+2 – управляющие точки.

Для трехмерных поверхностейопределяется два параметра (непрерывных) S и t, изменение которых дают координатулюбой точкина поверхности.

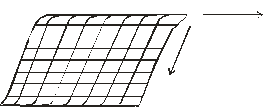
Фиксация одной переменной позволяют перейти к построению кривой на поверхности. Общая форма записи (для направления x):

x(S,t)=SCxT^T

где: Cx – коэффициенты кубического многочлена (для определения коэффициентов x, y соответственно Cy,Cz)

Для В-сплайна:

X(S,t)=SMsPxMs^TT^T

Y(S,t)=SMsPyMs^TT^T

Z(S,t)=SMsPzMs^TT^T

P – управляющие точки (16 точек)

(4 по S и 4 по t)

Матричное представление трехмерных преобразований.

Аналогично тому, как двумерные преобразования описываются матрицами размером 3х3, трехмерные преобразования могут быть представлены в виде матриц размером 4х4. И тогда трехмерная точка (x, y,z) записывается в однородных координатах как (Wx,Wy,Wz,W), гдеW0. ЕслиW1, для получения трехмерных декартовых координат точки (x,y,z) первые три однородные координаты делятся наW. Отсюда, в частности, следует , что две точкиH1 иH2 в пространстве однородных координат описывают одну и ту жеточку трехмерного пространства в том и только в том случае, когдаH1=сH2 для любой константы с, не равной нулю.

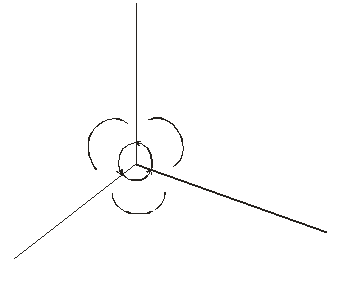
Трехмерная система координат является правосторонней. Примем соглашение, в соответствии с которым положительными будем считать такие повороты, при которых (если смотреть с конца положительной полуоси в направлении начала координат) поворот на 90против часовой стрелки будет переводить одну положительную полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:

Есть ось вращения	Положительным будет направление поворота
X Y Z	От YкZ От ZкX От XкY

Эти положительные направления отмечены также на рисунке.

Здесь применяется правосторонняя система координат, поскольку она хорошо знакома большинству людей, хотя в трехмерной графике чаще более удобна левосторонняя система, так как ее легче представить наложенной на поверхность экрана дисплея.

Это позволяет естественно интерпритировать тот факт, что точки с большими значениями zнаходятся дальше от наблюдателя. Отметим, что в левосторонней системе положительными будут повороты, выполняемые почасовой стрелке, если смотреть с конца положительной полуоси в направлении начала координат.

Трехмерный перенос является простым расширением двумерного

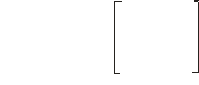
Т.е. [xyz1]*T(Dx, Dy, Dz) = [x+Dx y+Dy z+Dz 1]

Масштабирование расширяется аналогичным образом :

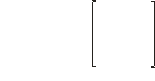
В трехмерном пространстве поорот вокруг оси zописывается выражением

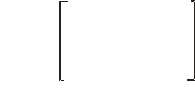
Результатом произвольной последовательности поворотов вокруг осей x,y,zявляется матрица А , имеющая вид

Подматрицу поворота размером 3х3 называют ортогональной, поскольку ее столбцы являются взаимно ортогональными единичными векторами. При повороте, задаваемом матрицей, эти единичные векторы совмещаются с осямиx,y,z. Иногда возникает необходимость определить матрицу поворота, соответствующую таким направлениям. Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и переноса не сохраняют.

Можно перемножить произвольное число матриц поворота, масштабирования и переноса. Результат всегда будет иметь вид:

Удаление невидимых линий и поверхностей

Задача удаления невидимых линий и поверхностей является одной из наиболее сложных задач в машинной графике. Алгоритмы удаления невидимых линий и поверхностей служат для определения линий ребер, находящегося в заданной точке пространства.

Все алгоритмы удаления невидимых линий (поверхностей) включают в себя сортировку координат объектов. Главная сортировка ведется по геометрическому расстоянию от тела, поверхности ребра или точки до точки наблюдения. Основная идея сортировки по расстоянию заключается в том, что чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заполнен одним из объектов, более близких к точке наблюдения. После определения расстояний или приоритетов по глубине остается провести сортировку по горизонтали и по вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения. Эффективность любого алгоритма удаления невидимых линий и поверхностей зависит от эффективности процесса сортировки.

Для повышения эффективности сортировки также когерентность сцены, т.е. тенденция неизменяемости характеристик схемы в малом.

Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают:

1. Алгоритмы, работающие в объектномпространстве, имеют дело с физической системой координат, в которой описаны эти объекты.

2. Алгоритмы, работающие в пространствеизображения, имеют дело с системой координат того экрана, на котором объекты визуализируются.

Первый способ более трудоемок, т.к. рассматриваются координаты объекта в МК, но преимущество состоит в том, что в ИМГ работая с объектом, возможна операция приближения, удаления части объекта (поворот) или всего объекта (трансфокация). При этом получается более реалистичное изображение (высокая точность). Объем вычислений для любого алгоритма, работающего в объектном пространстве, и сравнивающего каждый объект сцены, растет теоретически как квадрат числа объектов (n²).

Второй способ имеет точность вычислений ограниченную разрешающей способностью экрана, возможны искажения изображения (несовпадение концов отрезков, сопрягаемых поверхностей и т.п.), но при этом обладает высокой эффективностью. Объем вычислений алгоритма работающего в пространстве изображений и сравнивающего каждый объект сцены с позициями всех пикселов в системе координат экрана, растет теоретически, как nN(где,n– количество объектов,N– число пикселов).

Трудоемкость: То.п. < Тп.и. при n<N