1584

Метод «дерево целей» используется для прогнозирования сложных экономических процессов, систем, в которых возможно выделение многих структурных или иерархических уровней.

Процедура построения «дерева целей» представляет собой формулировку генеральной цели прогноза с последующим разбиением ее на ряд подцелей 1-го уровня, который является результатом реализации подцелей 2-го уровня, и т.д. При этом разбиение генеральной цели происходит как бы из будущего в настоящее с установлением промежуточных событий и фиксацией причинно-следственных связей между ними.

«Дерево целей» формируется с помощью экспертов, причем при переходе от уровня к уровню состав экспертов меняется. При приближении к более высокому уровню остаются более крупные эксперты в конкретных областях. В обязанности экспертов входят: а) формулировка системы целей (подцелей); б) присвоение коэффициентов относительной важности или весов элементам различных уровней «дерева целей». Построение «дерева целей» заканчивается, когда мы доходим до конкретных практических мероприятий, которые нельзя представить как результат реализации других мероприятий.

Этапы построения «Дерева целей»:

1)формулировка генеральной цели прогноза;

2)формулировка перечня подцелей различных уровней;

3)непосредственно построение «дерева целей»;

4)установление коэффициентов относительной важности различных узловых моментов «дерева целей» (с помощью экспертов);

5)разработка конкретных мероприятий по реализации поставленных целей прогноза;

6)выбор наиболее оптимальных мероприятий;

7)определение состава и объема ресурсов, необходимых для реализации выбранных мероприятий.

Раздел 3. Прогнозирование на основе корреляционнорегрессионных зависимостей

Тема 3.1. Использование статистических пакетов для регрессионного анализа

Основные вопросы темы: Формирование моделей. Вид полученных моделей. Исследование моделей, формулирование

полученных результатов.

Рекомендуемая литература: 1, 5.

Перечень дополнительных ресурсов: 2, 3, 4.

Наименование вида самостоятельной работы: Изучение литературы; оформление отчета о лабораторной работе; подготовка к тестированию.

Оценка параметров конкретного уравнения является лишь отдельным этапом длительного и сложного процесса построения эконометрической модели. Первое же оцененное уравнение очень редко является удовлетворительным во всех отношениях. Обычно приходится постепенно подбирать формулу связи и состав объясняющих переменных, анализируя на каждом этапе качество оцененной зависимости. Этот анализ качества включает статистическую и содержательную составляющую. Проверка статистического качества оцененного уравнения состоит из следующих элементов:

•проверка статистической значимости каждого коэффициента уравнения регрессии;

•проверка общего качества уравнения регрессии;

•проверка свойств данных, выполнение которых предполагалось

при оценивании уравнения.

Под содержательной составляющей анализа качества понимается рассмотрение экономического смысла оцененного уравнения регрессии: действительно ли значимыми оказались объясняющие факторы, важные с точки зрения теории; положительны или отрицательны коэффициенты, показывающие направление воздействия этих факторов; попали ли оценки коэффициентов регрессии в предполагаемые из теоретических соображений интервалы.

Методика проверки статистической значимости каждого отдельного коэффициента уравнения линейной регрессии была рассмотрена в предыдущей главе. Перейдем теперь к другим этапам проверки качества уравнения.

Проверка общего качества уравнения регрессии. Коэффициент детерминации r2

Для анализа общего качества оцененной линейной регрессии используют обычно коэффициент детерминации R2. Для случая

парной регрессии — это квадрат коэффициента корреляции переменных х и y. Коэффициент детерминации рассчитывается по формуле

.

Коэффициент детерминации характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. В качестве меры разброса зависимой переменной обычно используется ее дисперсия, а остаточная вариация может быть измерена как дисперсия отклонений вокруг линии регрессии. Если числитель и знаменатель вычитаемой из единицы дроби разделить на число наблюдений п, то получим, соответственно, выборочные оценки остаточной дисперсии и дисперсии зависимой переменной у. Отношение остаточной и общей дисперсий представляет собой долю необъясненной дисперсии. Если же эту долю вычесть из единицы, то получим долю дисперсии зависимой переменной, объясненной с помощью регрессии. Иногда при расчете коэффициента детерминации для получения несмещенных оценок дисперсии в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы; тогда

.

или, для парной регрессии, где число независимых переменных травно 1,

В числителе дроби, которая вычитается из единицы, стоит сумма квадратов отклонений наблюдений у iот линии регрессии, в знаменателе - от среднего значения переменной у. Таким образом, дробь эта мала (а коэффициент R2, очевидно, близок к единице), если разброс точек вокруг линии регрессии значительно меньше, чем вокруг среднего значения. МНК позволяет найти прямую, для ко-

знаменателе, - иначе выбираемой по МНК линией регрессии была бы прямая. Таким образом, коэффициент детерминацииR2является мерой, позволяющей определить, в какой степени найденная регрессионная прямая дает лучший результат для объяснения поведения зависимой переменной у, чем просто горизонтальная прямая.

Смысл коэффициента детерминации может быть пояснен и

ki=- отклонение i й точки на линии регрессии от.В данной формуле величина в левой части может интерпретироваться как мера общего разброса (вариации) переменной у, первое слагаемое в правой

части- как мера разброса, объясненного с помощью регрессии, и

второе слагаемое -как мера остаточного, необъясненного разброса (разброса точек вокруг линии регрессии). Если разделить эту формулу на ее левую часть и перегруппировать члены, то

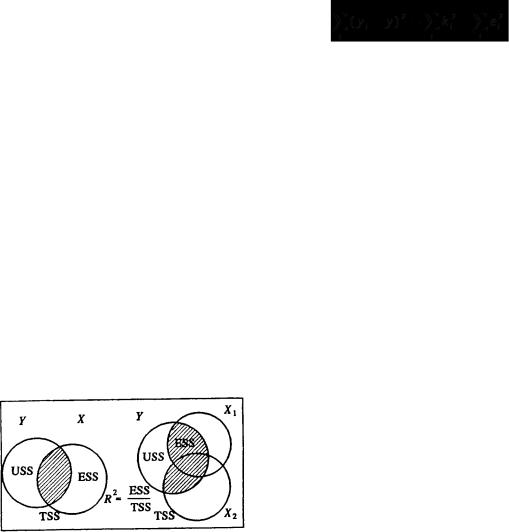
, то есть коэффициент детерминацииR2есть доля объясненной части разброса зависимой переменной (или доля объясненной дисперсии, если разделить числитель и знаменатель на n илип-1). Часто коэффициент детерминации R2иллюстрируют рис. 4.2

Рис. 4.2.

Здесь TSS (Total Sum of Squares) -общий разброс переменной у, ЕSS (Explained Sum of Squares) -разброс, объясненный с помощью регрессии, USS (Unexplained Sum of Squares)-разброс, необъясненный с помощью регрессии. Из рисунка видно, что с увеличением объясненной доли разброса коэффициентR2-приближается к единице. Кроме того, из рисунка видно, что с добавлением еще одной переменной R2 обычно увеличивается, однако если объясняющие переменныех1их2сильно коррелируют между собой, то они объясняют

существенно сужается: рассматриваются не все возможные прямые или гиперплоскости, а только проходящие через начало координат. ВеличинаR2получится отрицательной в том случае, если разброс значений зависимой переменной вокруг прямой (гиперплоскости) меньше, чем вокруг даже наилучшей прямой (гиперплоскости) из проходящих через начало координат. Отрицательная величинаR2 в

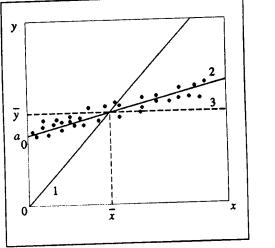
уравнении говорит о целесообразности введения в него свободного члена. Эта ситуация проиллюстрирована на рис. 4.3.

Линия 1 на нем - график уравнения регрессии без свободного члена (он проходит через начало координат), линия 2 - со свободным членом (он равен а0), линия 3 -.Горизонтальная линия 3 дает гораздо меньшую сумму квадратов отклонений еi, чем линия 1, и поэтому для последней коэффициент детерминацииR2будет отрицательным.

Рис. 4.3. Линии уравнений линейной регрессии у=f(х) без свободного члена (1) и со свободным членом (2)

Поправка на число степеней свободы всегда уменьшает значение R2, поскольку(п-1)>(п-т-1). В результате величинаR2также может стать отрицательной. Но это означает, что она была близкой к нулю до такой поправки, и объясненная с помощью уравнения регрессии доля дисперсии зависимой переменной очень мала.

Тема 3.2. Прогнозирование на основе классического регрессионного анализа. Выбор структуры модели

Основные вопросы темы: Формирование модели. Вид полученной модели. Исследование модели, формулирование полученных результатов.

Рекомендуемая литература: 1, 5.

Перечень дополнительных ресурсов: 2, 3, 4.

Наименование вида самостоятельной работы: Изучение литературы; оформление отчета о лабораторной работе; подготовка к тестированию.

Краткое содержание лекции, основные термины, понятия и определения темы

Регрессионные модели представляют собой определенные математические соотношения между показателями работы объекта или характеристиками наблюдаемого явления y1, y2,...,ye и теми вычислениями, которые их определяют x1, x2, xm.

Величины y1, y2, ye называют зависимыми переменными или откликами объекта, а величины x1, x2, xm – входными переменными, независимыми характеристиками или факторами.

Основные этапы построения регрессивной модели:

I. Получение экспериментальных данных.

Вначале необходимо упорядочить полученные экспериментальные данные.

х – опыты у – отклики

n – число опытов m – число факторов

Содержание предварительной обработки данных в основном состоит в отсеивании грубых погрешностей измерения или погрешностей возникающих при переписывании и вводе в ЭВМ полученных данных.

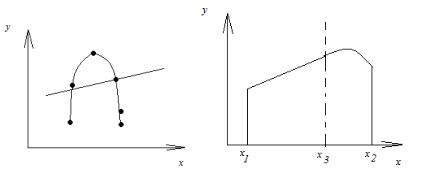
II. Выбор структуры модели.

Под структурой понимается вид модели, выбранные факторы, наиболее значимо влияющие на отклик, оптимальное количество факторов, определяемое имеющимися данными в наблюдениях.

Тема 3.3. Матричная форма МНК, оценка значимости регрессионных коэффициентов. Коэффициент детерминации. Анализ адекватности модели. Использование статистических пакетов для регрессионного анализа

Основные вопросы темы: Формирование модели. Вид полученной модели. Исследование модели, формулирование полученных результатов.

Рекомендуемая литература: 1, 5.

Перечень дополнительных ресурсов: 2, 3, 4.

Наименование вида самостоятельной работы: Изучение литературы; оформление отчета о лабораторной работе; подготовка к тестированию.

Краткое содержание лекции, основные термины, понятия и

полученное из опыта. Суть метода состоит в том что все остатки минимизировать с помощью метода наименьших квадратов.

n – количество опытов.

Регрессионные коэффициенты оцениваются исходя из минимизации Q. МНК оценки обладают рядом свойств, не зависящих от ряда распределения отклика и фактора. А именно эти оценки не смещены, эффективны и состоятельны.

yi*f1j в правую часть, так как они являются константами.