
- •Введение
- •1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР
- •1.1. Предмет теории игр
- •1.2. Формальное описание игры
- •1.3. Классификация игр
- •2.1. Платёжная матрица. Принцип минимаксной и максиминной стратегий
- •2.2. Решение игр в смешанных стратегиях
- •2.5. Решение игры в доминирующих стратегиях
- •2.6. Сведение матричной игры к задаче линейного программмирования
- •3. ИГРЫ С ПРИРОДОЙ
- •Критерии оптимальности
- •Контрольная работа
Выделяя |
в |
«дополнительном» столбце |
(строке) |
наибольшее |
(наименьшее) число, находим нижнюю цену 1 и верхнюю цену |
||||
игры 1. |
В |
данном случае получаем |
равенство |
1. |
Максиминной стратегией будет A2 , а минимаксными – две стратегии
B1 и B3.
Пример 3. Определить нижнюю и верхнюю цены игры, заданной платёжной матрицей
С |
0,5 |
0,6 0,8 |
|
||
|
0,7 |
0,8 |
|
||
P 0,9 |
. |
||||
|
0,6 |
0,6 |
|
||
|
|
0,7 |
|
||
Имеет |
гра седловую точку? |
|
|
||
Решен е. Для удо ства проведём все расчёты в табл. 2, в |
||||||||||
ли |
|
|
|
|
|
|
||||
которой введём платёжную матрицу, столбец i , состоящий из |
||||||||||
минимальных элементов строк, и строку |
j, |
составленную из |
||||||||
максимальных элементов стол цов. |
|
|
|
|
|
Таблица 2 |
||||
Из табл. 2 |
найдём, |
что нижняя и |
|
|
|
|
||||
|
|
|
|
|
||||||
|
B1 |
B2 |
B3 |
αi |
||||||
верхняя цены |
игры |
соответственно |
|
|||||||
A1 |
0,5 |
0,6 |
0,8 |
0,5 |
||||||
равны |
|
|
|
|
||||||
|
|
|
|
A2 |
0,9 |
0,7 |
0,8 |
0,7 |
||
max i max(0,5;0,7;0,6) 0,7; |
|
|
|
|
|
|
||||
|
A3 |
0,7 |
0,6 |
0,6 |
0,6 |
|||||
|
бА |
|
|
|
|
|
||||
|
βj |
0,9 |
0,7 |
0,8 |
0,7 |
|||||
min j min(0,9;0,7;0/8) 0,7. |
|
|||||||||
Значения 0,7 достигаются |
|
|
|
|
|
|||||
|
|
|
|
|
||||||
на одной и той же паре стратегий (A2,B2). Следовательно, игра имеет |
||||||||||
седловую точку (A2,B2)и цена игры |
0,7. |
|
|
|
|
|||||
|
|
|
Д |
|||||||
2.2. Решение игр в смешанных стратегиях |
|
|
|
|||||||
Если игра не имеет седловой точки, тоИоптимальное решение игры нельзя найти в чистых стратегиях. В этом случае можно получить оптимальное решение, случайным образом применяя чистые стратегии.
Смешанной стратегией SA игрока A называется применение чистых стратегий A1,A2,...,Am с вероятностями p1, p2,..., pm , причём
17
m
сумма вероятностей равна единице: pi 1. Смешанные стратегии
i 1
SA игрока A записываются в виде матрицы
|
A ...A...A |
|
|
|
SA |
1 |
i m |
|
|
p ...p ....p |
|
|
||
|
1 |
i |
m |
|
или в в де строки SA (p1, p2,..., pm). |
|
|
|
|
||
Аналог чно смешанные стратегии SB игрока B записываются в |
||||||
виде матр цы |
|
|
|
|
|
|
С |
|
B ...B |
...B |
|
||
S |
|
1 |
j |
|
n |
|
|
B |
q ...q ....q |
n |
|
||
|
|
1 |
i |
|
|
|
в в де строки SB (q1,q2,...,qn), где |
n |
|
|
|||
qj |
1. |
|||||
или |
|
|
|
j 1 |
|
|
Из определен я смешанной стратегии следует, что любая чистая |
||||||
стратег я грока является смешанной, в которой все стратегии, кроме |
||||||
бА |
||||||
одной, имеют нулевые вероятности. |
|
|
|
|
||
На основании принципа минимакса оптимальное решение игры |
||||||
– это пара оптимальных смешанных стратегий (S A;S B), обладающих свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры. Цена игры удовлетворяет условию , где
и – нижняя и верхняя цены игры. |
|
|
|
И |
|
Теорема Неймана. Каждая конечная игра имеет одно |
||
оптимальное решение, возможно,Дсреди смешанных стратегий. |
||
Пусть S A (p 1, p |
2,..., p m) и S B (q 1,q |
2,...,q n) – пара |
оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.
Теорема об активных стратегиях. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры , если второй игрок не выходит за пределы своих активных стратегий.
Пусть игрок A выбрал свою чистую i-ю стратегию с вероятностью pi , а игрок B свою j-ю чистую стратегию с
18
вероятностью qj . Ситуация, определяемая этими стратегиями, имеет
вероятность |
pi qj . |
Таким образом, |
процесс |
игры можно |
рассматривать как некоторое случайное испытание, исходами |
||||
которого будут ситуации игры. |
|
|
||
Пусть |
случайная |
величина X – |
ситуация |
в смешанных |
стратегиях. |
Она принимает значения P (aij),i 1,2,...,m; j 1,2,...,n, |
|||
с соответствующ ми вероятностями (pi |
qj), |
i 1,2,...,m; j 1,2,...,n. |
|||||||||||||
Найдём математ ческое ожидание случайной величины X : |
|||||||||||||||
|
|
|
|
|
|
m |
n |
|
|
|
|
|
|
|
|
СMX aij piqj . |
|
|
|
|
|
(5) |
|||||||||
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
|
|
|
Математ ческое ожидание |
MX |
называется |
математическим |
||||||||||||
ем |
вы грыша |
игрока |
A |
или |
|
математическим |
ожиданием |
||||||||
ожидан |
|
|
|
|
|
|
|
|
|
|
|||||
проигрыша |
грокаB. |
|
|
|
|
|
|
|
10 |
30 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
. Найти |
||||
Пр мер 4. Дана платёжная матрица игры P |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
математическое ожидание выигрыша игрока A. |
40 |
|
|
||||||||||||
|
|
|
|
|
|||||||||||
Решение. Находим нижнюю и верхнюю цены игры: |
|
|
|
||||||||||||
max i max(10;20) 20, |
min j min(40;30) 30. |
||||||||||||||
Так |
как , |
то |
матрица |
не |
имеет |
седловой |
точки. |
||||||||
СледовательнобА, оптимальные стратегии надо искать во множестве |
|||||||||||||||
смешанных |
стратегий. |
Обозначим |
SA (p1, p2) |
– |
смешанная |
||||||||||
стратегия |
игрока |
A, где |
p1 p2 1; |
SB (q1,q2) |
– |
смешанная |
|||||||||
стратегия игрокаB, где q1 q2 |
1. Найдём математическое ожидание |
||||||||||||||
|
|
|
|
|
|
|
|
m |
n |
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||
выигрыша игрока A по формуле MX aij piqj |
или распишем |
||||||||||||||
|
|
|
|
|
|
|
i 1 j 1 |
|
|
|
|
|
|
||
MX a11 p1 q1 a12 p1 q2 a21 p2 q1 a22 p2 q2. |
|
|
|
||||||||||||
Определим |
значения |
вероятностей |
p1 , p |
, |
при |
которых |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
математическое ожидание выигрыша игрокаИA максимально, а также |
|||||||||||||||
значения вероятностей q1, q2 , при которых математическое ожидание проигрыша игрокаB – минимально.
Подставляя в последнее выражение для математического ожидания значения вероятностей p2 1 p1 и q2 1 q1, получаем
19
MX 10p1q1 |
30p1q2 40p2q1 20p2q2 |
10p1q1 30(1 p1)q1 |
40(1 p1)q1 |
20(1 p1) (1 q1). |
|
|
После группировки членов двумя способами можно записать |
||||||||||||||||||||||||||||||||
выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
MX 40p |
(q |
|
) 20(q 1), с другой стороны, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
1 |
|
1 |
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MX 40q (p |
|
1 |
) 10(p 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||
|
Анал з руя полученные формулы, делаем вывод, что при q |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|||
и |
любых |
значен ях |
p1, p2 0 |
|
математическое |
|
ожидание |
||||||||||||||||||||||||||
MX |
|
1 |
б |
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
20( |
|
1) 25. |
|
Аналогично, |
если |
|
|
и |
вероятности |
||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
q1,q2 0 пр |
н мают лю ые значения, MX 10( |
|
|
1) 25. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
1 |
|
3 |
|
|
|
|
|||||||||||||||||
|
Таким |
о разом, |
если |
|
|
SA |
( |
1 |
, |
1 |
) |
|
и |
|
|
SB |
( |
, |
), |
то |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
математическое ожидание выигрыша игрока |
A или математическое |
||||||||||||||||||||||||||||||||
ожидание проигрыша игрокаB |
|
удет равно MX 25. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Вывод. Стратегия SA |
( |
1 |
, |
1 |
) с выигрышем MX 25 для игрока |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A является предпочтительнее получения достоверного выигрыша, |
|||||||||||||||||||||||||||||||||
равного 20, хотя нельзя исключать получение самого малого |
|||||||||||||||||||||||||||||||||
выигрыша, равного 10. |
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Платёжная функция u(p,q) игры в смешанных стратегиях |
||||||||||||||||||||||||||||||||
определяется как математическоеДожидание (среднее значение) этой |
|||||||||||||||||||||||||||||||||
случайной величины и, следовательно, выражается формулой |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(p,q) aij pi qj . |
|
|
|
|
|
|
|
|
|
|
|
(6) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В теории игр переход к случайному выбору стратегий называется смешанным расширением игры, стратегии исходной игры называются чистыми, а сама исходная игра – игрой в чистых стратегиях.
20
Чистой стратегии |
Ai |
поставим в соответствие смешанную |
||||||
стратегию p(i) (0,...,1,...,0), |
где число 1 стоит на i-м месте, т.е. во |
|||||||
всех |
партиях |
применение |
p(i) заключается в выборе |
Ai |
с |
|||
вероятностью 1. Аналогично связаны чистая стратегия |
Bj |
и |
||||||
смешанная стратегия |
q(i) =(0, …,1, …,0), где число 1 стоит на |
j-м |
||||||
|
|
|
|
|
m n |
|
|
|
месте. |
Из |
формулы |
|
u(p,q) aij pi qj |
следует, |
|
что |
|
|
|
|
|
|
i 1j 1 |
|
|
|
u(p(i) ,q( j))=aij =u(Ai,Bj ) |
в |
конечной игре и паре ( p(i) ,q( j)) в |
её |
|||||
смешанном расш рен |
соответствует один и тот же результат. Это |
|||||||
С |
|
|
|
|
|
|
||
означает, что ч стые стратегии можно считать частными случаями |
||||||||
смешанных, а гру в чистых стратегиях – частным случаем игры в смешанных стратег ях. Будем называть чистыми не только стратегии
выигрыш игрока A и проигрыш игрока B (в случаях, когда один из игроков применяет чистую стратегию). Нетрудно проверить, что значение платёжной функции в общем случае выражается через эти величины по формуле
|
гры, |
но |
соответствующие им смешанные стратегии, а |
|||
|
(i) (i) |
|
|
|
|
|
исходной |
|
|
|
|||
вместо p |
q |
п |
сать просто Ai и Bj. В этих обозначениях замена |
|||
p на p(i) = (0, …,1, …,0) в формуле (6) запишется в виде |
|
|||||
|
|
|
|
n |
|
|
|
|
|
u(Ai,q) aij |
qj,1 i m. |
(7) |
|
|
|
|
|
j 1 |
|
|
Аналогично получаем |
|
|
|
|||
|
бА |
|
||||
|
|
|
|
m |
|
(8) |
|
|
|
u(p,Bj) aij pi,1 j n. |
|||
|
|
|
|
i 1 |
|
|
Величины |
u(Ai,q) и u(p,Bj) |
представляют собой средние |
||||
|
|
|
|
Д |
|
|
|
|
|
|
|
И |
|
m |
n |
|
u(p,q) pi |
u(Ai,q) qj u(p,Bj). |
(9) |
i 1 |
j 1 |
|
21
|
|
Величины |
(p) minu(p,q) и (q) |
maxu(p,q) |
называются |
||||||||||
гарантированным выигрышем стратегии |
p и гарантированным |
||||||||||||||
проигрышем стратегии q. |
|
|
|
|
|
|
|
|
|||||||
|
|
Числа |
|
|
max(min u( p,q)) max ( p) |
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С |
|
|
|
называются |
нижней ценой и верхней |
||||||||||
min (q) min(maxu(p,q)) |
|||||||||||||||
ценой игры |
в |
смешанных стратегиях. |
Стратегия p (стратегия q) |
||||||||||||
называется макс м нной (минимаксной), если (p) ; (q) |
; |
||||||||||||||
максим нные |
|
|
|
минимаксные |
стратегии |
называются |
|||||||||
|
ми |
|
|
|
|
|
|
|
|
||||||
гарант рующ |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
В любой матр чной игре выполнены неравенства |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
бА |
|
|
|||||||||||
|
|
2.3. Анал т ческ й метод решения игры размера 2×2 |
|||||||||||||
|
|
Если |
гра размера 2 2 имеет седловую точку, то оптимальное |
||||||||||||
решение – это пара чистых стратегий, соответствующих этой точке. Если в игре отсутствует седловая точка, то согласно теореме
Неймана оптимальное решение существует и определяется парой
смешанных стратегий S A (p 1, p |
2) |
и S B (q 1,q |
2). |
|
|
|
|
|||||||||||||||||||
|
Пусть игра задана платёжной матрицей |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|||||||
а игроки |
используют |
свои |
смешанные |
стратегии |
|
A |
A |
|
|
и |
||||||||||||||||
|
SA 1 |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дp p |
2 |
|
|
||||||||||||||
|
B |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
SB |
1 |
q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение цены игры согласно формуле (6) можно записать так: |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||
|
a |
|
p q a |
p |
q |
a |
21 |
p |
q a |
22 |
p |
q или |
|
|
|
|
||||||||||
|
|
11 |
1 |
1 |
12 |
1 |
2 |
|
|
2 |
|
1 |
|
|
2 |
|
2 |
|
|
|
|
|||||
|
p (a q a |
q ) p (a |
21 |
q |
a |
22 |
q ). |
|
|
|
|
|
|
|||||||||||||
|
|
1 |
11 |
1 |
12 |
2 |
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
Так как p1 p2 1, то выражения в скобках равны .
22
Таким образом, оптимальные стратегии игрока Bи цену игры можно найти из системы уравнений
|
|
|
|
|
|
|
|
a q |
a q |
; |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
1 |
|
|
|
12 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
(10) |
|||
|
|
|
|
|
|
|
|
a21q1 |
a22q2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По |
|
аналог |
|
|
для |
|
нахождения |
оптимальной |
стратегии |
игрока |
||||||||||||||||||||||
B надо реш ть с стему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
оптимальныерешен я значение цены игры: |
|
|
|
|
|
|||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a11p1 a21p2 ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
(11) |
|||
|
|
|
|
|
|
|
|
|
a12 p1 |
a22 p2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пр меняя, |
|
напр мер, |
|
формулы |
Крамера, получим искомые |
|||||||||||||||||||||||||||
|
|
|
|
a22 |
a21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a22 a12 |
|
|
|
|
|
|||||||
p1 |
a |
a |
|
|
a |
|
a |
|
|
; |
q1 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||
22 |
|
|
|
|
a |
|
a |
22 |
a |
a |
21 |
|
||||||||||||||||||||
|
11 |
|
12 |
|
|
|
|
|
21 |
|
|
|
|
11 |
|
|
12 |
|
|
|
||||||||||||
|
|
|
|
a11 |
a12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 a21 |
|
|
|
|
|
||||||
p2 |
|
|
|
|
|
|
|
|
|
|
; q2 |
a |
|
a |
|
a |
a |
; |
(12) |
|||||||||||||
a |
a |
22 |
a |
|
a |
21 |
|
22 |
||||||||||||||||||||||||
|
11 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
12 |
|
|
21 |
|
||||||||
|
|
a22 a11 a12 a21 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
aбa a a А |
|
|
|
|
||||||||||||||||||||||||||
|
11 |
22 |
|
12 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 5. Платёжная матрица имеет вид |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
1,5 |
|
3 |
|
|
И |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
Найти оптимальное решение и цену игры. |
|
|
|
|
|
|||||||||||||||||||||||||||
Решение. Находим нижнюю и верхнюю цену игры: |
|
|||||||||||||||||||||||||||||||
max i max(1,5;1) 1,5; min j min(2;3) 2. |
|
|||||||||||||||||||||||||||||||
Следовательно, и игра не имеет седловой точки, |
значит, |
|||||||||||||||||||||||||||||||
она решается в смешанных стратегиях. Так как игра размера 2 2, то её можно решить аналитическим методом.
23
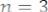
Пусть оптимальные смешанные стратегии игроков A и B соответственно равны S A (p 1, p 2) и S B (q 1,q 2). Для нахождения этих стратегий и цены игры составим и решим системы уравнений (10), (11) по вышеуказанным формулам (12):
С |
|
|
|
|
|
|
|
|
; |
|
|
|
1.5q |
3q |
; |
|
|||||||||||
|
|
1.5p 2p |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
3p1 1 p2 ; |
|
|
|
|
2q1 |
1 q2 |
|
||||||||||||||||||
|
|
|
|
|
p |
|
1; |
|
|
|
|
|
|
|
|
|
q |
|
1. |
|
|||||||
|
|
p |
|
2 |
|
|
|
|
|
|
q |
|
|
|
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
||||
В результате получаем оптимальные стратегии и цену игры: |
|||||||||||||||||||||||||||
S |
|
|
|
|
|
|
S |
|
(0,8;0,2); 1,8. |
|
|
|
|
|
|
|
|||||||||||
A (0,6;0,4); |
B |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
бы |
|
|
|
|
|
|
|
|
|
||||||||||||||||
2.4. Граф ческое решение игр вида (2×n) и (m×2) |
|
||||||||||||||||||||||||||
иГраф ческ й метод применяется для решения матричных игр, в |
|||||||||||||||||||||||||||
которых хотя |
|
од н |
грок имеет только две стратегии. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
А |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Решение игры размера |
2 n |
|
|||||||||||||||
Пусть |
|
. Рассмотрим частный случай – игру (2 3), которая |
|||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
задается матрицей |
|
|
11 |
12 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
a |
|
|
|
a |
|
|
a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Введём обозначения: |
X x1,x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
•для |
игрока |
|
|
|
|
A: |
|
|
– |
|
|
смешанная |
стратегия, |
||||||||||||||
X* x1*,x2* – оптимальная смешанная стратегия игрока, где |
|||||||||||||||||||||||||||
x1,x2 0; x1 x2 1; |
|
* |
|
* |
|
|
* |
|
|
|
* |
|
|
|
|
|
|||||||||||
|
x 1,x 2Д0; x 1 x 2 1; |
||||||||||||||||||||||||||
•для |
игрока |
B: |
Y |
* y |
*,y |
*,y |
* |
|
|
– |
оптимальная |
смешанная |
|||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
стратегия, |
1; |
|
y |
* |
0; |
j 1,2,3; |
y |
|
– |
первая чистая стратегия, |
|||||||||||||||||
y* |
|
|
|||||||||||||||||||||||||
|
|
j |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
– третья чистаяИстратегия. |
|||||||||||
y2 – вторая чистая стратегия, |
y3 |
||||||||||||||||||||||||||
Пусть игрок |
|
A |
|
|
применил свою смешанную стратегию X , а |
||||||||||||||||||||||
игрок B – свою первую чистую стратегию y1.
Математическое ожидание выигрыша игрока A будет равно
M x a11x1 a21x2 a11x1 a21 1 x1 a11 a21 x1 a21.
24
Пусть игрок A применил свою смешанную стратегию X , а игрок B – свою вторую чистую стратегию y2.
Математическое ожидание выигрыша игрока A:
M x a12x1 |
a22x2 a12x1 a22 1 x1 a12 a22 x1 a22. |
|
|||||||||
С |
A применил свою смешанную стратегию X , а |
||||||||||
Пусть игрок |
|||||||||||
игрок B – свою третью чистую стратегию. |
|
|
|||||||||
Математ ческое ожидание выигрыша игрока A находится по |
|||||||||||
длины |
|
|
|
|
|||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
M x a13x1 a23x2 a13x1 a23 1 x1 a13 a23 x1 a23. |
|
||||||||||
|
бА |
|
|
||||||||
В декартовой с стеме координат откладываем по оси абсцисс |
|||||||||||
отрезок ед н чной |
|
|
. Левый конец отрезка соответствует |
||||||||
стратег |
A1, правый – стратегии A2 . |
|
|
|
|||||||
Построим прямые: |
|
|
|
|
|
|
|
||||
y a11 a21 x1 a21; |
|
|
|
|
|
||||||
|
a12 a22 x1 a22; |
|
|
|
|
|
|||||
y |
Д |
|
|||||||||
y |
a |
a |
23 |
x a |
23 |
. |
|
||||
|
13 |
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
Ломаная, |
полученная |
при |
|
И |
|||||||
построении прямых |
1 , |
2 , 3 |
|||||||||
(рис. 1), определяет нижнюю границу математического ожидания |
|||||||||||
выигрыша игрока A. |
|
|
|
|
|
|
x*; . |
||||
Точка M с наибольшей ординатой имеет координаты M |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
На рис. 1 |
точка |
M находится на пересечении прямых |
и 2 , |
||||||||
поэтому её координаты находим, решив систему уравнений 1 |
и 2 . |
||||||||||
Выявим активные стратегии игрока B. |
Это будут первая и вторая, |
||||||||||
соответствующие |
прямым |
1 и |
2 , |
а третья чистая |
стратегия |
||||||
игроком Bне применяется, т.е. y3* 0.
25
Тогда оптимальная стратегия Y игрока B будет иметь вид Y y1*,y2*,0 . Найдём ее по уменьшенной матрице игры:
С |
|
a |
|
a |
|
|
a |
|
a |
a |
|
|
|
|
|
|
|
|
||||||
|
|
11 |
12 |
|
|
13 |
|
11 |
12 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a21 |
a22 |
|
a23 |
|
a21 |
a22 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В |
тоге получ ли |
|
игру размера (2 2), которую можно решить |
|||||||||||||||||||||
аналит ческ м методом, рассмотренным выше. |
|
|
|
|
|
|
|
|
||||||||||||||||
матрицей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
игры, |
|||||||||
Пр мер 6. Найти оптимальное решение и значение цены |
||||||||||||||||||||||||
заданной платёжной |
|
|
|
|
|
2 |
3 |
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
4 |
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
бА |
|
|
|
|
|
|
|
|||||||||||||||
Решен е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Дана матр ца |
|
гры |
(2 4), т.е. игрок |
I имеет |
две чистые |
|||||||||||||||||||
стратег |
, |
а грок |
II |
– |
четыре: |
1, |
2, |
|
3, 4. Пусть |
X x1,x2 |
– |
|||||||||||||
смешанная |
стратег я |
|
игрока |
|
I; |
X* x1*,x2* |
|
– |
оптимальная |
|||||||||||||||
смешанная стратегия игрока I, |
где |
x ,x |
2 |
0; |
x |
x |
2 |
1; |
|
x*1,x*2 0; |
||||||||||||||
x*1 x*2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для игрока |
II: чистые |
|
стратегии – 1, 2, 3, 4; оптимальная |
|||||||||||||||||||||
смешанная |
стратегия |
|
Y |
|
|
Д |
|
|
||||||||||||||||
|
y*, |
y*, y*, y* |
, |
где |
|
y* |
, y*, y*, y* 0; |
|||||||||||||||||
4 |
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
4 |
|
|
|
|
1 |
|
2 |
3 |
4 |
|
yj 1. Решение |
игры |
(2 4) |
проводим |
с |
позиции |
|
игрока |
A, |
||||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
придерживающегося максиминной стратегии. |
|
|
|
|
|
|
|
X , а |
||||||||||||||||
2. Пусть игрок I применил свою смешанную стратегию |
||||||||||||||||||||||||
игрок II – соответственно 1, 2, 3, 4 чистые стратегии. Получим |
||||||||||||||||||||||||
математическое ожидание M x выигрыша игрока I: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2x1 4x2 M x ; |
|
M x 2x1 4; |
|
|
|
|
|
|||||||||||||||
|
|
|
|
1x2 |
M x ; |
|
|
M x 2x1 1; |
|
|
|
|
|
|
||||||||||
|
|
3x1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
6x2 |
M x ; |
|
|
|
И |
|||||||||||||||
|
|
1x1 |
|
M x 5x1 6; |
|
|
|
|
|
|||||||||||||||
|
|
5x 0x |
2 |
M x . |
|
|
|
M x 5x . |
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3. Построим прямые:
26
y 2x1 4; 1 |
|
||
|
y 2x 1; |
2 |
|
С |
|
||
|
1 |
|
|
y 5x 6; 3 |
|
||
|
1 |
4 |
|
y 5x . |
|
||
|
1 |
|
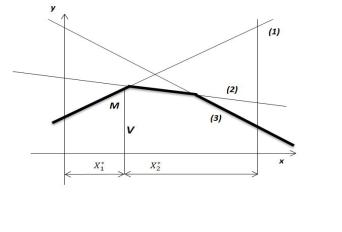
Рис. 2 |
|
|
|
|
точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Прямая (1) соответствует чистой стратегии 1, прямая (2) – чистой |
|||||||||||||||||||||||
стратег 2, прямая (3) – чистой стратегии 3, прямая (4) – чистой |
|||||||||||||||||||||||
стратег |
4 |
грока II. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
бА7 7 |
|
|
|
|
||||||||||||||||||
На р с. 2 точка |
M |
|
находится на пересечении прямых (2) и (3), |
||||||||||||||||||||
поэтому коорд наты |
|
|
M находим, решив систему уравнений |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
y 2x1 |
1; |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y 5x1 |
|
|
|
|
|
||||||||||
Получим x |
x* |
|
5 |
, |
тогда x* |
1 x* |
|
2 |
. Оптимальная смешанная |
||||||||||||||
|
|
||||||||||||||||||||||
|
|
1 |
1 |
7 |
|
|
|
2 |
|
|
|
1 |
|
7 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||||||||
стратегия игрока I будет равна X |
|
|
|
5 |
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
; |
|
. |
|
|
|
|
|
||||||||||||
4. Значение |
цены игры |
находится |
|
из |
уравнения (2) или |
(3). |
|||||||||||||||||
Подставляя значение x |
x* |
5 , получим y 2x* 1 |
17 |
. |
|
||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
7 |
|
|
|
|
|
|
|
|
|
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
5. Для нахождения оптимальной смешанной стратегии игрока II |
|||||||||||||||||||||||
выявим |
его |
активные |
чистые |
стратегии. Так как |
точка M x* |
,V |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
находится на пересечении прямых (2) и (3), то активные чистые |
|||||||||||||||||||||||
стратегии игрока II будут вторая |
и третья. Прямые (1) и (4) |
не |
|||||||||||||||||||||
задействованы, следовательно, игрок II свои чистые стратегии 1 и 4 |
|||||||||||||||||||||||
не применяет, т.е. |
* |
|
|
* |
0. Оптимальная смешанная стратегия |
||||||||||||||||||
y1 |
0; y4 |
||||||||||||||||||||||
игрока |
II |
имеет |
|
вид |
Y |
y* 0;y* |
;y* |
;y* 0 , |
находится |
по |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
3 |
4 |
|
|
|
|
||
уменьшенной матрице игры без 1 и 4 чистых стратегий игрока II, |
|||||||||||||||||||||||
которая имеет вид |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
27
6. Получили игру (2 2), для которой оптимальные стратегии и
цена |
игра |
находятся |
из системы уравнений |
3y* |
y* |
; |
|
|
|||||||||||||||
|
2 |
|
|
3 |
|
|
|
где |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y2* 6y3* |
, |
|
|
||||||||
y* y* 1; |
y* |
y* 0. Решив систему, |
получим |
|
y* |
|
5 |
; y* |
2 |
. |
|||||||||||||
|
|
|
|||||||||||||||||||||
С7 |
|
|
|
|
|
|
|
|
|
2 |
|
7 |
|
3 |
7 |
|
|||||||
2 |
3 |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Y |
* |
|
|
5 |
|
2 |
|
|
|
|
|
|
|
|
Оптимальная смешанная стратегия игрока II: |
|
0; |
7 |
; |
7 |
;0 . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. Так м образом, оптимальное решение игры (X ;Y ), |
значение |
||||||||||||||||||||||
минимакса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
цены игры |
17 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. Анал з |
стратег й |
игроков. Применим |
принцип |
|
максимина |
и |
|||||||||||||||||
|
|
к стратег ям игроков I и II. Игроку I гарантируется |
|||||||||||||||||||||
|
бАa a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
выигрыш от 0 до 1, а |
гроку II о еспечен проигрыш от 3 до 6. |
|
|
|
|||||||||||||||||||
Смешанные стратег |
|
X |
и Y гарантируют игроку I выигрыш не |
||||||||||||||||||||
менее 17 2,43 , а |
гроку II проигрыш не более 2,43. |
|
|
|
|
|
|||||||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение игры (m 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При решении игры (m 2) рассуждаем так же, что и для игры |
|||||||||||||||||||||||
(2 n). Пусть |
m 3 |
. |
|
Д |
|
|
|||||||||||||||||
Получим игру размера ( |
3 2) |
с платёжной |
|||||||||||||||||||||
матрицей |
|
|
11 |
12 |
Смешанные стратегии |
игроков |
I и |
II |
|||||||||||||||
P a21 |
a22 . |
||||||||||||||||||||||
|
|
|
|
a |
a |
|
|
И |
|||||||||||||||
|
|
|
|
31 |
|
32 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
X x1,x2,x3 ; Y y1,,y2, , где |
|
|
3 |
|
|
||||||||||
обозначим соответственно |
|
|
xi 1; |
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
1; xi |
0,yj 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Построим |
|
не |
нижнюю, а верхнюю границу ломаной |
||||||||||||||||||||
математического ожидания выигрыша игрока I. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
М x a11y1 a12 y2 a11 a12 y1 a12; М x a21y1 a22 y2 a21 a22 y1 a22 ; М x a31y1 a32 y2 a31 a32 y1 a32.
28
Построим прямые: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x a11 a12 y1 a12; 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
a22 y1 a22; 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x a21 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x a |
31 |
a |
32 |
y a |
32 |
. 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
стратегии |
|
|
|
|
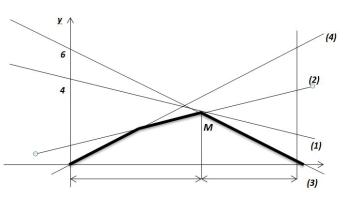
Рис. 3 |
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
с минимальной |
|||||||||||||||
С2. На верхней ломаной находим точку M |
|||||||||||||||||||||
ординатой. Орд ната точки M соответствует значению цены игры , |
|||||||||||||||||||||
а абсц сса – компоненте смешанной стратегии игрока II, т.е. M y*, . |
|||||||||||||||||||||
|
|
|
бА |
|
|
|
1 |
||||||||||||||
3. Определяем акт вные стратегии игрока I. Так как прямая (1) |
|||||||||||||||||||||
соответствует ч |
|
стой |
|
|
|
|
|
|
x игрока I, прямая (2) – его чистой |
||||||||||||
стратег |
|
x2, прямая (3) |
– его чистой стратегии |
x3, то на рис. 3 |
|||||||||||||||||
активные |
стратег |
– первая и вторая, чистая стратегия 3 не |
|||||||||||||||||||
применяется, т.е. оптимальная смешанная стратегия игрока I будет |
|||||||||||||||||||||
X* x*,x*,x* |
0 , где x* |
и x* |
находят, |
рассматривая уменьшенную |
|||||||||||||||||
|
1 |
2 |
3 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
матрицу игры: |
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
11 |
12 |
Д |
|
||||||||||
|
|
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a |
21 |
a |
22 |
|
|
11 |
12 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
||
|
|
|
|
|
|
|
a31 |
a32 |
|
|
|
|
|
|
|
|
|
||||
Для решения игры применим аналитический метод. |
|
|
|
||||||||||||||||||
Пример |
7. |
Найти |
решение |
|
и |
|
|
И |
|||||||||||||
|
значение |
цены |
игры, |
заданной |
|||||||||||||||||
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
платёжной матрицей 4 |
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
Дана |
матрица игры |
размера |
|
(3 2). |
Для игрока |
I: |
чистые |
|||||||||||||
стратегии 1, 2, 3; оптимальная смешанная стратегияX x*,x*,x* . |
|||||||||||||||||||||
Для |
игрока |
II: |
чистые |
стратегии |
1, |
2; |
смешанная |
1 |
2 |
3 |
|||||||||||
стратегия |
|||||||||||||||||||||
29
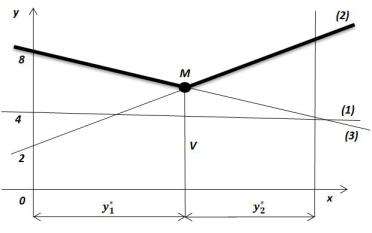
Y y1,y2 , оптимальная смешанная стратегия Y y1*,y2* , причем
3 |
; x* |
2 |
|
y* 0. |
|
|
|
|
x* 1 |
0; y* 1; |
|
|
|
||||
i |
i |
j 1 |
j |
j |
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
2.Пусть игрок II применил свою смешанную стратегию, а игрок I – |
||||||||
С |
|
|
|
|
|
|
||
соответственно 1, 2, 3 чистые стратегии. |
||||||||
3. Запишем математическое ожидание выигрыша игрока I: |
||||||||
|
|
|
M x 2y1 4y2 2y1 4; |
|||||
|
|
|
|
|
|
|
|
|
и |
|
y2 |
3y1 1; |
|||||
|
|
|
M |
x 4y1 |
||||
|
|
|
M x 2y 8y |
2 |
6y 8. |
|||
|
|
|
|
|
1 |
|
1 |
|
4.Постро м прямые |
|
|
|
|
|
|||
|
бА |
|||||||
x 2y1 |
4; 1 |
|
|
|
|
|
|
|
|
|
1; 2 |
|
|
|
|
|
|
x 3y1 |
|
|
|
|
|
|
||
x 6y 8. 3 |
|
|
|
|
|
|
||
|
1 |
|
|
|
Д |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
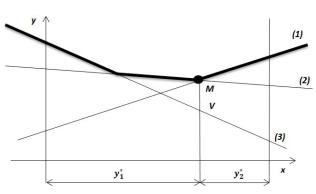
Рис. 4 |
Прямые (1), (2), (3) соответствуют первой, второй и третьей чистым стратегиям игрока I соответственно и выделяют верхнюю границу математического ожидания проигрыша игрока II. Находим точку M с
наименьшей ординатой на ломаной: |
M y*, . На рис. |
4 |
точка M |
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
находится на пересечении прямых (2) и (3), следовательно, |
|||||||||||||||||
координаты точки найдем, решив систему уравнений (2) и (3). |
|||||||||||||||||
Получим y |
y* |
7 |
; |
y |
|
1 y* |
2 |
. |
|
И |
|||||||
9 |
|
9 |
|
|
|
|
|
|
|
|
|
||||||
1 |
1 |
|
|
2 |
1 |
|
|
|
|
|
7 |
|
2 |
|
|||
Оптимальная смешанная стратегия игрока II будет Y |
|
|
|
||||||||||||||
|
|
|
; |
|
. |
||||||||||||
|
|
9 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
||
30
5. Значение цены игры найдем, используя одно из уравнений (2)
или (3) при y |
|
y* |
|
7 |
. Из уравнения (2) получим x 3y* 1 |
10 |
. |
||||||||||||||||||||
|
9 |
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|||
6. Для нахождения оптимальной смешанной стратегии игрока I |
|||||||||||||||||||||||||||
определим |
|
его |
|
активные |
чистые стратегии. Так как точка M |
||||||||||||||||||||||
находится на пересечении прямых (2) и (3), активными стратегиями |
|||||||||||||||||||||||||||
являются чистые стратегии 2 и 3, чистую стратегию 1 игрок не |
|||||||||||||||||||||||||||
применяет. |
|
|
Опт мальная |
смешанная |
стратегия |
игрока |
I |
будет |
|||||||||||||||||||
X |
0;x*;x* |
. |
Не звестные компоненты находим по уменьшенной |
||||||||||||||||||||||||
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. Решив систему, |
получим |
|||||||
матрицегде x x 1, т.к. x |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
4 |
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сгры 4 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
бА |
|
|
|
|
|
|||||||||||||||||||
7. Получ ли |
гру (2 x 2), для которой составим систему уравнений |
||||||||||||||||||||||||||
4x* 2x* |
; |
|
|
|
* |
* |
|
|
* |
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x* |
8x* |
, |
|
|
|
|
2 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
2 |
2 |
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
* |
|
* |
|
|
. |
Оптимальная смешанная стратегия игрока I |
будет |
||||||||||||||||||||
x2 |
;x3 |
|
3 |
||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
равна X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0; |
|
; |
|
|
. |
|
Д |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 3 |
|
|
|
|
|
|||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, оптимальное решение игры X ,Y , |
значение |
||||||||||||||||||||||||||
цены игры |
|
|
|
|
10 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. |
Анализ стратегий игроков. |
Применим принцип максимина и |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
минимакса к стратегиям игроков I и II: |
4 |
1 1 |
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
8 |
|
|
|
|
|
|
|
Игроку |
|
|
I |
гарантируется выигрыш |
от |
1 до |
2, игроку |
II – |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проигрыш от 4 до 8. Смешанные стратегииИX и Y гарантируют |
|||||||||||||||||||||||||||
игроку I выигрыш не менее |
10 |
3,33 , а игроку II – проигрыш не |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
более 3,33 .
31
