1476

Решение.

В соответствии с первым законом термодинамики изменение внутренней энергии термодинамической системы ∆U определяется работой Авнеш внешних сил и переданным системе количеством теплоты Q:

Внутренняя энергия U для случая двухатомного идеального газа равна

U 5 m RT, 2 M

где m – масса газа;

М – молярная масса газа;

R – универсальная газовая постоянная; Т – абсолютная температура.

Тогда

Работа, совершенная над газом, очевидно, равна разности начальной и конечной кинетической энергий поршня. В момент максимального сжатия газа поршень неподвижен, следовательно,

Полученный результат представляет собой лишь оценку изменения температуры газа, т. к. в расчетах не учитывались такие явления, как распад молекул и ионизация атомов водорода при высокой температуре.

Ответ: ∆T = 2,4.105 К.

41

Лекция 7

РЕАЛЬНЫЕ ГАЗЫ

К данной лекции студент должен

–знать, в чем заключается модель идеального газа, уравнение Менделеева – Клапейрона, что называется изопроцессами;

–уметь объяснить свойства газов, исходя из модели идеального

газа,

–уметь изобразить графики изопроцессов.

План лекции

1.Причины отклонения реальных газов от модели идеального газа (собственный объем молекул, взаимодействие молекул газа).

2.Уравнение Ван-дер-Ваальса.

3.Изотермы реальных газов. Критическая температура.

4.Ожижение газов.

5.Примеры решения задач.

Литература

-С. 117 – 119. § 60. Силы и потенциальная энергия межмолекулярного взаимодействия.

-С. 119 – 120. §61. Уравнение Ван-дер-Ваальса.

-С. 120 – 122. §62. Изотермы Ван-дер-Ваальса и их анализ. -С. 125 – 126. § 65. Сжижение газов.

Вопросы для самоконтроля

1.Обоснуйте, проведя расчет, что при высоких давлениях (сотни и тысячи атмосфер) значительная часть объема газа приходится на собственный объем молекул.

2.Начертите и прокомментируйте график зависимости сил межмолекулярного взаимодействия от расстояния между молекулами газа, график потенциальной энергии взаимодействия молекул от расстояния между ними.

3.Запишите уравнение Ван-дер-Ваальса. Обоснуйте введение поправок в уравнение.

4.Чем изотермы реального газа отличаются от изотерм идеального газа?

42

5. Что называют критической температурой? В чем заключается значимость данного понятия для практики?

Тест

1. Характерный размер молекулы составляет…

1. 10-6 см. 2. 10-6 м. 3. 10-8 см. 4. 10-8 м. 5. 10-13 см.

2. Уравнение состояния для 1 моля реального газа имеет вид…

1. PV RT . 2. p = nkT. 3. PV m RT .

3. На рис. 15 приведены изотермы Ван-дер-Ваальса. Какая из изотерм соответствует критической

4. Для ожижения газа, нахо-

Рис. 15

дящегося при температуре выше критической, необходимо…

1.Сжать газ до давления, не превышающего критическое.

2.Сжать газ до давления, превышающего критическое.

3.Сжать газ до произвольного давления.

4.Увеличить объем газа в изотермическом процессе.

5.Предварительно понизить температуру газа так, чтобы она была меньше критической.

5. В современных промышленных установках ожижения газов применяют

1.Поршневые машины, в которых газ охлаждается за счет совершения им работы.

2.Турбодетандеры, в которых газ охлаждается за счет совершения им работы.

3.Машины Линде, работающие на основе эффекта ДжоуляТомсона.

43

4.Машины Линде, в которых газ предварительно охлажден ниже температуры инверсии.

5.Машины Линде, в которых газ предварительно нагрет выше температуры инверсии.

Примеры решения задач

Задача 7.1

В определенном интервале расстояний энергия взаимодействия молекул реального газа U(r) зависит от расстояния r между частицами:

U r A , r6

где А – постоянная для данного вещества величина, А > 0.

Во сколько раз изменится сила притяжения между молекулами при изменении расстояния на 1 %?

Решение.

Сила взаимодействия F равна

F dU . dr

Тогда

F1 r27 ;

F2 r17

F1 1,07.

F2

Ответ: F1 1,07.

F2

Задача 7.2

Оцените, во сколько раз изменится расстояние между молекулами воды при переходе воды из жидкого в газообразное состояние (при нормальном атмосферном давлении).

Решение.

Вычислим, какой объем V1 приходится на долю одной молекулы воды в жидком состоянии:

V

V1 NA ,

где V – объем, занимаемый одним молем воды; NA – число Авогадро.

V M ,

44

где М – молярная масса воды; ρ – ее плотность.

Тогда

M

V1 NA ;

V1 10183 610103 23 3 10 29 м3 .

Расстояние между центрами соседних молекул d1 будет равно d1 3V1 ;

d1 33 10 29 3 10 10 м .

Рассмотрим теперь водяной пар при нормальном атмосферном давлении и температуре 1000С. Объем V, занимаемый одним молем водяного пара при этих условиях, можно определить, воспользовавшись уравнением Менделеева – Клапейрона:

pV = RT,

где p – давление водяного пара;

R – универсальная газовая постоянная; T – абсолютная температура пара.

V RT . p

Объем V2 , приходящийся на долю одной молекулы водяного пара при этих условиях:

V

V2 NA ;

Среднее расстояние между молекулами d2 равно

d2 3V2 ;

d2 3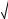5 10 26 3,7 10 9 м .

Получив численные характеристики распределения в пространстве молекул вещества в жидкости и газообразном состояниях, сравним их между собой:

Расчеты показывают, что при переходе воды из жидкого состояния в газообразное при условиях, близких к нормальным, объем, приходящийся на долю одной молекулы, увеличивается почти в 2000 раз. Однако среднее расстояние между молекулами увеличивается не так значительно.

Задача 7.3

В вертикально расположенном цилиндре под поршнем находится один моль углекислого газа при температуре T, равной удвоенной критической температуре Tкр. Объем газа V равен критическому объему Vкр. Какая сила F должна быть приложена к поршню, чтобы он находился в равновесии? Массу поршня не учитывать. Трения между внутренней стенкой цилиндра и поршнем нет, внешним давлением пренебречь. Площадь поперечного сечения поршня S = 5 см2 , критическое давление углекислого газа 73 атм.

Решение.

Давление p углекислого газа должно уравновешивать давление, создаваемое внешней силой, приложенной к поршню:

где a и b – постоянные Ван-дер-Ваальса, характеризующие соответственно силы межмолекулярного взаимодействия и собственный объем молекул газа.

Критические объем, давление и температура выражаются через

27 Rb

Учитывая, что по условию задачи

T = 2Ткр;

6 Трофимова Т.И. Курс физики: учеб. пособие для вузов.– 13-е изд., стер. – М.: Издательский центр «Академия», 2007. – С. 121.

46

V = Vкр,

определим из соотношений (50) – (53) давление газа:

P = 5Pкр .

Тогда из (49) легко определить силу F:

F 5 pкр s;

F = 5.73.105.5.10-4 = 18000 (Н).

F = 18 кН.

Ответ: F = 18 кН.

Лекция 8

ЯВЛЕНИЯ ПЕРЕНОСА

К данной лекции студент должен

–знать основное уравнение МКТ идеального газа, какова связь абсолютной температуры и средней энергии поступательного движения молекул идеального газа;

–уметь применять основные соотношения МКТ идеального газа для расчета давления, концентрации газа, скорости движения молекул газа.

План лекции

1.Среднее число столкновений и средняя длина свободного пробега молекул идеального газа.

2.Закон Фика. Диффузия газов.

3.Закон Фурье. Теплопроводность газов.

4.Вакуум. Свойства разреженных газов.

5.Примеры решения задач.

Литература

-С. 91 – 92. § 46. Среднее число столкновений и средняя длина свободного пробега молекул.

-С. 94 – 96. § 48. Явление переноса в термодинамических неравновесных системах.

-С. 97 – 98. § 49. Вакуум и методы его получения. Свойства ультраразрежённых газов.

47

Вопросы для самоконтроля

1.От каких физических величин зависит среднее число столкновений и средняя длина свободного пробега идеального газа?

2.Запишите формулу закона Фика. Поясните, какие величины определяют скорость процесса диффузии. Какими физическими величинами определяется коэффициент диффузии газов?

3.В чем заключается процесс теплопроводности? Какими математическими соотношениями описывается данный процесс?

4.Сравните механизмы теплопроводности плотных и разреженных газов.

5.Какое состояние газа принято называть вакуумом?

3. Как изменится среднее число столкновений за 1 с молекул газа при уменьшении температуры газа в 4 раза?

1. Увеличится в 4 раза. 2. Увеличится в 2 раза. 3. Не изменится. 4. Уменьшится в 2 раза. 5. Уменьшится в 4 раза.

4. Во время зимы толщина ледяного покрова на озере увеличилась в 2 раза. Как изменилась при этом величина теплового потока,

48

проходящего через лед? Температуру окружающего воздуха считать постоянной.

1. Увеличилась в 4 раза. 2. Увеличилась в 2 раза. 3. Не изменилась. 4. Уменьшилась в 2 раза. 5. Уменьшилась в 4 раза. 5. Между двумя стенками колбы термоса находится разреженный

газ. При этом процесс теплопроводности между стенками колбы…

1.Протекать не будет.

2.Обусловлен переносом энергии молекулами газа от одной стенки к другой.

3.Обусловлен выравниваем средних кинетических энергий газа за счет столкновений их друг с другом.

4.Протекает так же, как и в случае заполнения пространства между стенками плотным газом.

5.Уменьшается при увеличении концентрации газа между стенками колбы.

Примеры решения задач

Задача 8.1

Как зависит сила тока I, при которой происходит перегорание проводника, от диаметра проводника D?

Решение.

При прохождении тока по проводнику выделяется некоторое количество теплоты (джоулево тепло), что приводит к повышению температуры проводника. В результате возникает градиент температур между проводником и окружающей средой, что вызывает отвод тепловой энергии в окружающую среду через поверхность проводника. В соответствии с законом Джоуля – Ленца количество теплоты dQвыд, выделяющееся за времяdt, равно