
393
.pdf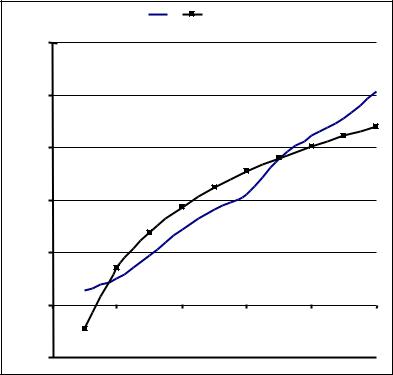
ПОИСК ЭМПИРИЧЕСКИХ
ЗАВИСИМОСТЕЙ
ПО ЭКСПЕРИМЕНТАЛЬНЫМ
ДАННЫМ
Методические указания к лабораторным работам
для студентов инженерных специальностей
|
|
y |
y1= |
aLn(x)+b |
|
|
25,00 |
|
|
|
|
|
|
20,00 |
|
|
|
|
|
|
15,00 |
|
|
|
|
|
|
10,00 |
|
|
|
|
|
|
5,00 |
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
0 |
2 |
4 |
|
6 |
8 |
10 |
-5,00 |
|
|
|
|
|
|
Федеральное агентство по образованию
ГОУ ВПО «Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра «Информационные технологии»
ПОИСК ЭМПИРИЧЕСКИХ
ЗАВИСИМОСТЕЙ
ПО ЭКСПЕРИМЕНТАЛЬНЫМ
ДАННЫМ
Методические указания к лабораторным работам
для студентов инженерных специальностей
Составитель Ю.Г. Аверьянов
Омск
СибАДИ
2
2009
УДК 004.42 ББК 32.97
Рецензент д-р техн. наук, доц. Б.А. Алексашенко (ОмТИИ)
Работа одобрена научно-методическим советом специальностей 190205, 190603, 220301, 190500 в качестве методических указаний к лабораторным работам для студентов инженерных специальностей.
Поиск эмпирических зависимостей по экспериментальным данным:
Методические указания к лабораторным работам для студентов инженерных специальностей / Сост. Ю.Г. Аверьянов. Омск: СибАДИ, 2009. 24 с.
В методических указаниях приведены математическая модель поиска эмпирических зависимостей по экспериментальным данным, алгоритм решения средствами Excel и блок-схема программы на VBA.
Табл. 3. Ил. 9. Библиогр.: 4 назв.
ГОУ «СибАДИ», 2009
3
ВВЕДЕНИЕ
Методические указания разработаны с целью оказания помощи студентам при изучении прикладного приложения информатики.
Винженерной практике для математического описания того или иного процесса используются экспериментальные данные. Как правило, это функциональные зависимости, заданные таблично. Получение аналитической зависимости, описывающей данный процесс таблично, и является задачей настоящих методических указаний.
Вметодических указаниях приводится пример аппроксимации эмпирической формулой, имеющей два параметра. Данная работа способствует развитию у студентов навыков работы с таблицами, графиками и ПК.
ПОСТАНОВКА ЗАДАЧИ АППРОКСИМАЦИИ
Допустим, две величины x и y связаны некоторой неизвестной зависимостью y=f(x). В результате n наблюдений получены значения f(x) в точках х1, х2, х3, х4, …, хп.
y1=f(x1); y2=f(x2); y3=f(x3),…,yn= f(xn).
Поскольку характер функциональной зависимости между x и y в самом общем случае неизвестен, то, используя вышеуказанные наблюдения, необходимо подобрать аналитическую формулу, отражающую с достаточной степенью точности эту зависимость.
Полученную по результатам наблюдений формулу можно использовать для дальнейших исследований методами математического анализа, вычислить промежуточные значения функции y=f(x) и т.п.
Определение аналитической зависимости между x и y, т.е. построение эмпирической формулы слагается из двух этапов: 1) подбор общего вида искомой величины; 2) определение параметров этой зависимости. Вся методика основана на методе наименьших квадратов.
4
Подбор аналитической зависимости по методу наименьших квадратов
Искомая зависимость называется математической моделью и в общем виде выглядит
y = f(x, b0, b1, b2…). |
(1) |
В самом общем случае вид уравнения регрессии (1) неизвестен, поэтому он определяется эмпирически.
Эмпирическая линия регрессии представляет собой чертеж с нанесенными экспериментальными точками в заданном масштабе.
По виду эмпирической линии регрессии можно судить о характере связи между x и y, что, в конечном счете, определяет вид искомого уравнения регрессии y=f(x).
Когда определен вид уравнения регрессии, переходят к определению конкретных коэффициентов этого уравнения. Определение коэффициентов уравнения регрессии производится из условия наименьшего отклонения экспериментальных точек от линии регрессии, соответствующей уравнению (1). Для этого используют метод наименьших квадратов.
Сущность этого метода состоит в следующем. Допустим, имеется выборка объема N, которая сведена в табл. 1.
Таблица 1
Исходные данные
x1 |
x2 |
x3 |
…xN |
|
|
|
|
y1 |
y2 |
y3 |
…yN |
|
|
|
|
Задача определения параметров уравнения регрессии сводится к определению минимума функции многих переменных. Требуется подобрать в0 , в1 , в2 ,…так, чтобы
N |
2 |
|
|
yi |
f (xi ,в0,в1,в2...) |
min, |
(2) |
i 1
5

т.е. сумма квадратов разностей между значениями искомой функции и экспериментальными значениями была минимальной.
Необходимыми условиями минимума функции (2) являются:
|
0; |
|
0; |
|
0… |
|
|
|
|||
в0 |
в1 |
в2 |
|||
Отсюда, учитывая выражения (1) и (2), имеем:
N
2 yi
i 1
N
2 yi
i 1
N
2 yi
i 1
f (xi ,в0,в1,в2...) f (хi ) 0;
в0
f (xi ,в0,в1,в2...) f (хi ) 0;
в1
f (xi ,в0 ,в1,в2...) f (хi ) 0.
в2
После преобразования получим:
(3)
(4)
N |
f (x ) |
N |
f (x |
) |
|
|
|
|
|
|||||
yi |
|
i |
|
|
f (xi,в0,в1,в2...) |
|
|
i |
|
|
0; |
|
||
|
в0 |
|
|
в0 |
|
|
|
|||||||
i 1 |
|
i 1 |
|
|
|
|
|
|
|
|
||||
N |
|
f (x ) |
N |
|
|
f (x ) |
|
|||||||
yi |
|
i |
f (xi ,в0,в1,в2...) |
|
|
i |
|
|
0; |
(5) |
||||
|
в1 |
|
в1 |
|
|
|||||||||
i 1 |
|
i 1 |
|
|
|
|
|
|
||||||
N |
|
f (xi ) |
|
N |
|
f (xi ) |
|
|
|
|||||
yi |
|
f (xi,в0,в1,в2...) |
0. |
|
||||||||||
|
в2 |
|
|
|||||||||||
i 1 |
|
i 1 |
|
|
в2 |
|
|
|
|
|||||
Как видно из соотношений (3), в этой системе будет столько уравнений, сколько неизвестных коэффициентов в0, в1, в2,… в уравнении регрессии (1).
Однако систему (5) нельзя решить в общем виде. Для ее решения нужно задаться видом уравнения регрессии.
Наиболее часто в качестве математических зависимостей при обработке экспериментальных данных методом наименьших квадратов принимаются следующие зависимости:
1)линейная у=ax+b;
2)степенная у=bха;
3)показательная вида у=bеах;
6
4)показательная вида у=baх;
5)логарифмическая у=aLn(x)+b;
6)гиперболическая у=b+a/x;
7)дробно-рациональная вида у=1/(ax+b);
8)дробно-рациональная вида у=x/(bx+a).
Линейная зависимость является наиболее простой математической моделью, которую используют при обработке экспериментальных данных методом наименьших квадратов. Однако практически исследователю при изучении зависимостей между x и y приходится чаще всего встречаться с нелинейной зависимостью. В таком случае целесообразно подобрать новые переменные u=f(x,y) и v=f(x,y) такие, чтобы между u и v , была линейная зависимость. Такой прием называется выравниванием вышеуказанных нелинейных зависимостей.
Отметим, что в новой системе координат значения искомых параметров (a и b) могут совпадать с их значениями в первоначальной системе координат, а могут отличаться и находиться по некоторым формулам. Поэтому обозначим их в новой системе координат заглавными буквами A и B и укажем соответствующие формулы перехода.
1. Пусть y является степенной функцией от x.
y = bхa . |
(6) |
Прологарифмируем равенство (6):
Ln( y)= aLn(x)+Ln(b).
Введём новые переменные:
u=Ln(x); v=Ln(y). |
(7) |
Тогда получим
v = Aи+B,
где |
a=A; B=Ln(b); b=exp(B). |
(8) |
Новые переменные u и v связаны линейной зависимостью. 2. Пусть y является показательной функцией от x.
7
|
y=beax. |
|
(9) |
|
Прологарифмируем равенство (9): |
|
|
|
Ln(y)=ах+Ln(b). |
|
|
|
Введём новые переменные: |
|
|
|
u=х; v=Ln(y). |
(10) |
|
|
Тогда получим |
|
|
|
v=Au+B, |
|
|
где |
a=A; B=Ln(b); |
b=exp(B). |
(11) |
|
Новые переменные связаны линейной зависимостью. |
|
|
|
3. Пусть y является показательной функцией от x. |
|
|
|
y = bax. |
(12) |
|
|
Прологарифмируем равенство (12): |
|
|
|
Ln(y)=хLn(a)+Ln(b). |
|
|
|
Введём новые переменные: |
|
|
|
u=х; v=Ln(y). |
(13) |
|
|
Тогда получим |
|
|
|
v=Au+B, |
|
|
где |
A=Ln(a); a=exp(A); |
B=Ln(b); b=exp(B). |
(14) |
|
Новые переменные связаны линейной зависимостью. |
|
|
|
4. Пусть y является логарифмической функцией от x. |
|
|
|
у=aLn(x)+b. |
(15) |
|
|
Введём новые переменные: |
|
|
|
u=Ln(х); |
v=y. |
(16) |
|
Тогда получим |
|
|
|
v=Au+B, |
|
|
где |
a=A; |
b=B. |
(17) |
8
Новые переменные связаны линейной зависимостью. 5. Пусть y является гиперболической функцией от x.
у=b+a/x. (18)
Введём новые переменные:
u=1/x; v=y. |
(19) |
Тогда получим
v=Au+B,
где |
a=А; b=B. |
(20) |
Новые переменные связаны линейной зависимостью. 6. Пусть y является дробно-рациональной функцией от x.
у=1/(ax+b). (21)
Введём новые переменные:
u=x; v=1/y. |
(22) |
Тогда получим
v=Au+B,
где |
a=A; b=B. |
(23) |
Новые переменные связаны линейной зависимостью. 7. Пусть y является дробно-рациональной функцией от x.
у=x/(bx+a). (24)
Введём новые переменные:
u=1/x; v=1/y. |
(25) |
Тогда получим
v=Au+B,
где |
a=A; b=B. |
(26) |
Новые переменные связаны линейной зависимостью.
Если искомое уравнение регрессии представляет собой линейную зависимость
9
y=ax+b, |
(27) |
то согласно выражению (3) получим:
у |
1; |
у |
х. |
(28) |
|
|
|||
в |
a |
|
||
При этом система (5) будет иметь вид:
N |
N |
N |
|
a xi2 b xi |
yi xi ; |
(29) |
|
i 1 |
i 1 |
i 1 |
|
N |
|
N |
|
a xi |
Nb yi . |
(30) |
|
i 1 |
|
i 1 |
|
Отсюда по формулам Крамера находим параметры уравнения
(27):
NN
N xi2 ( xi )2 ;
i 1 i 1
N N N
1 N xi yi xi yi ;
i 1 |
i 1 |
i 1 |
N N N N
2 xi2 yi xi yi xi ;
i 1 |
i 1 |
|
i 1 |
i 1 |
|||
a |
1 |
|
; |
b |
2 |
. |
|
|
|
||||||
|
|||||||
|
|||||||
|
|
|
|
||||
(31)
(32)
(33)
(34)
Если искомое уравнение регрессии представляет собой нелинейную зависимость от одного аргумента, то предварительно необходимо перейти к новым координатам по одной группе из двух формул (7, 10, 13, 16, 19, 22, 25). Соответствующие формулы метода наименьших квадратов будут иметь следующий вид:
10
