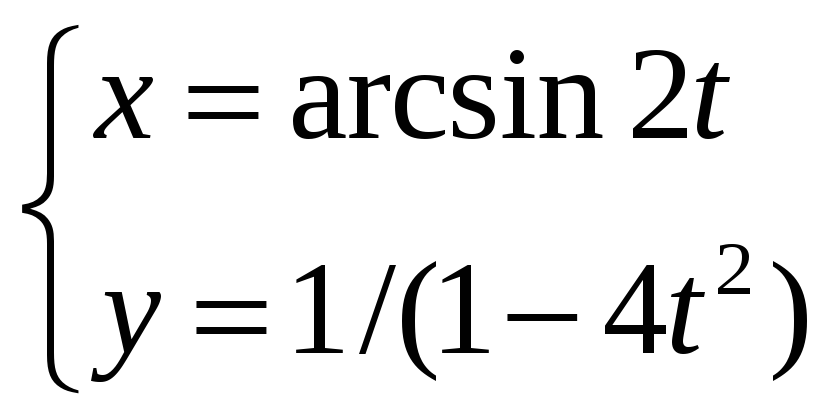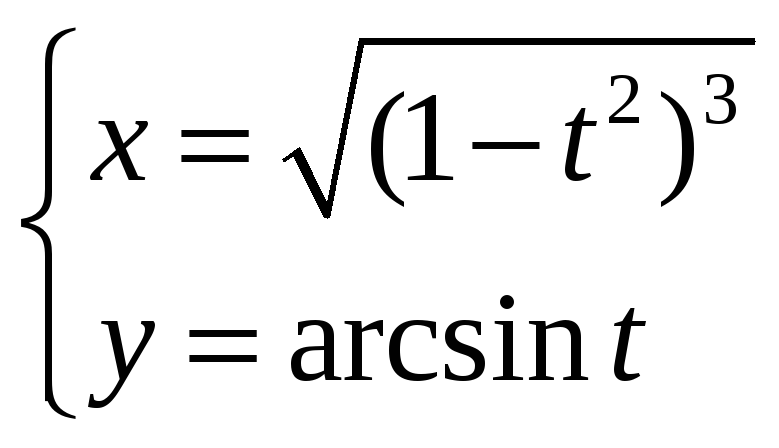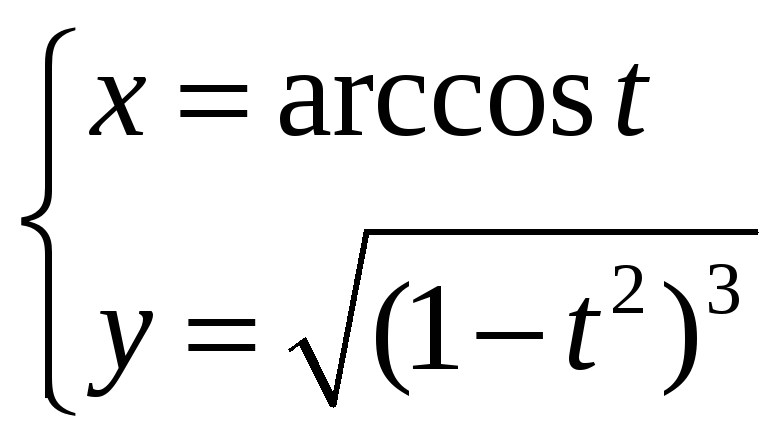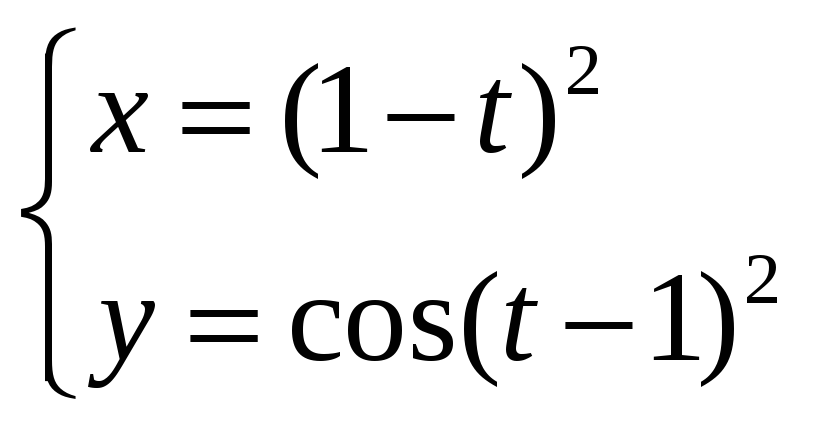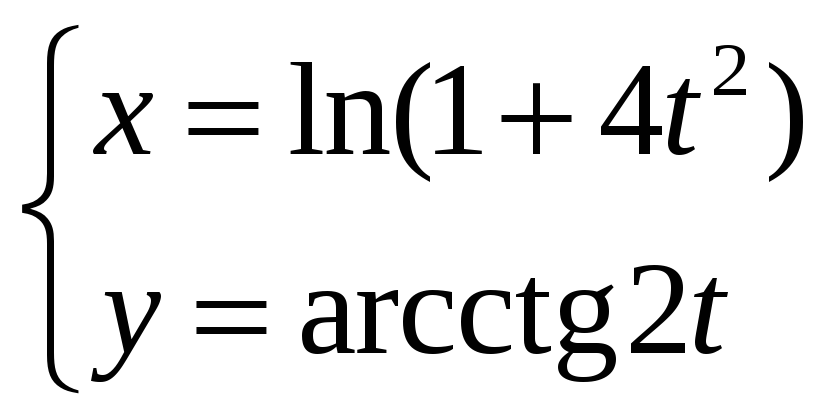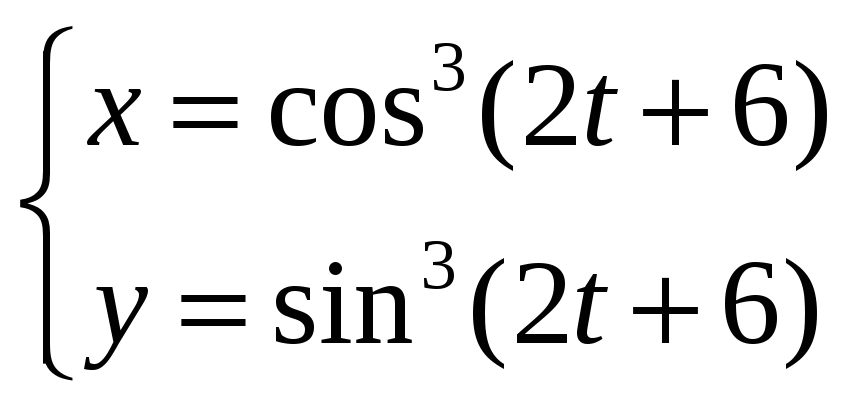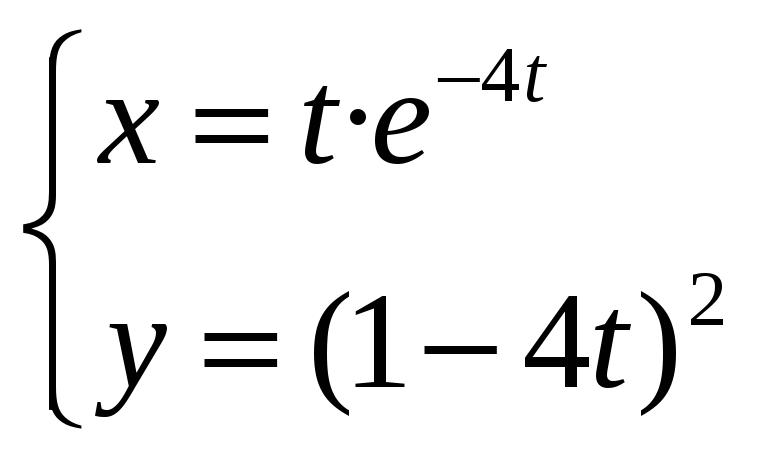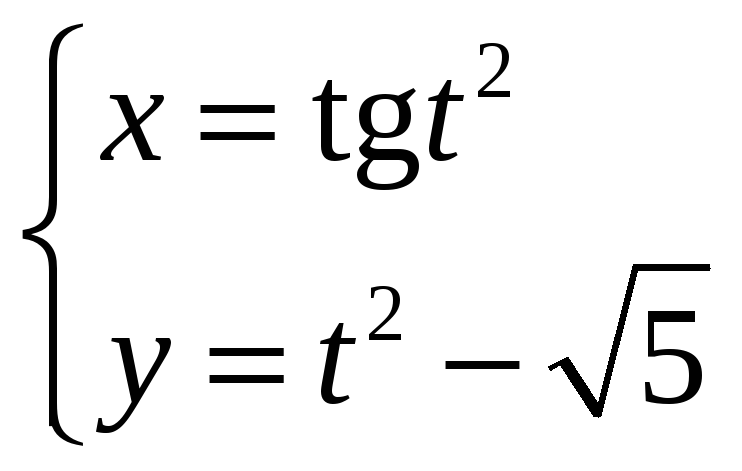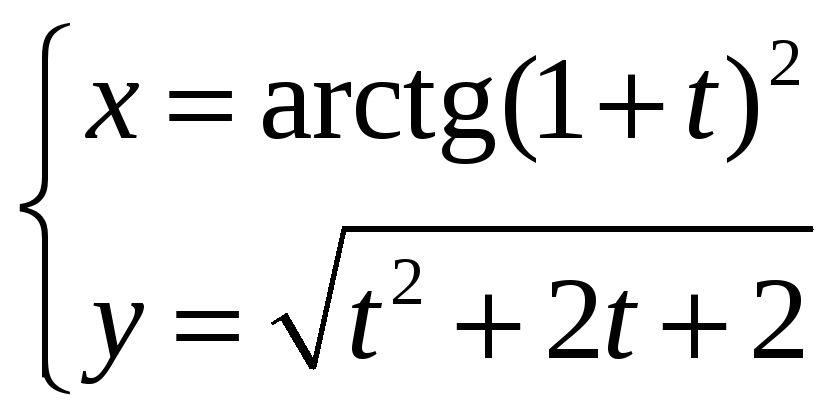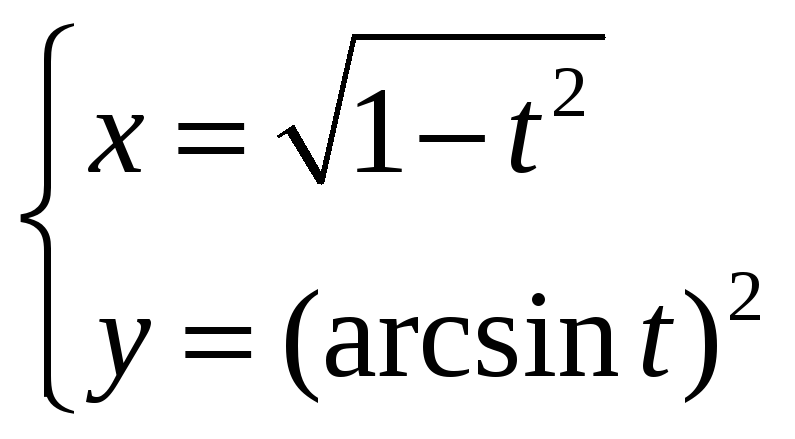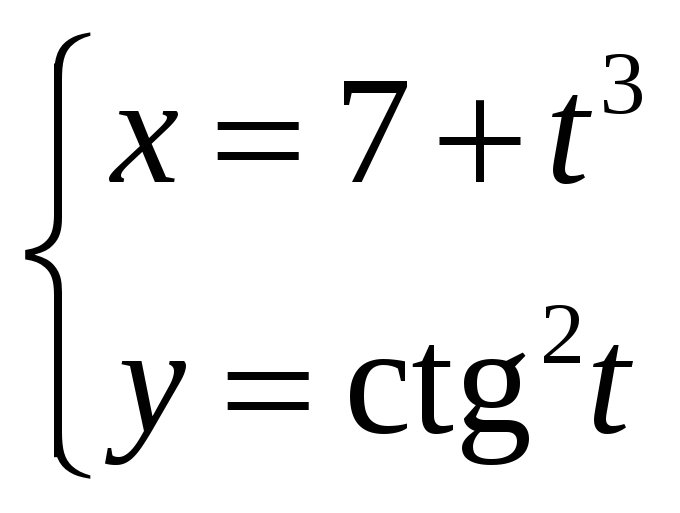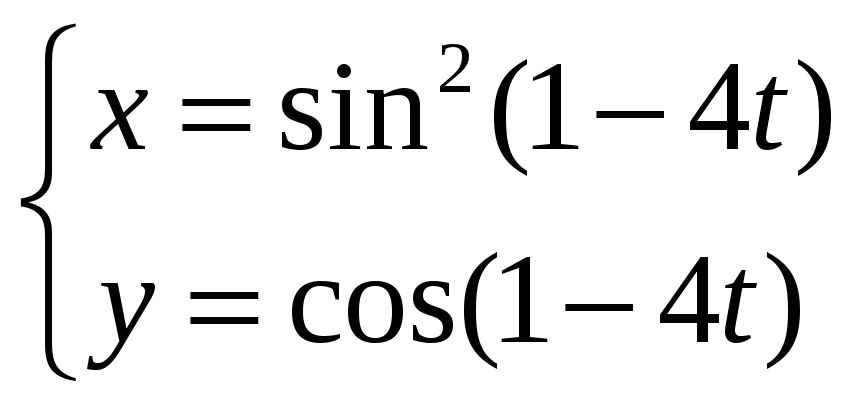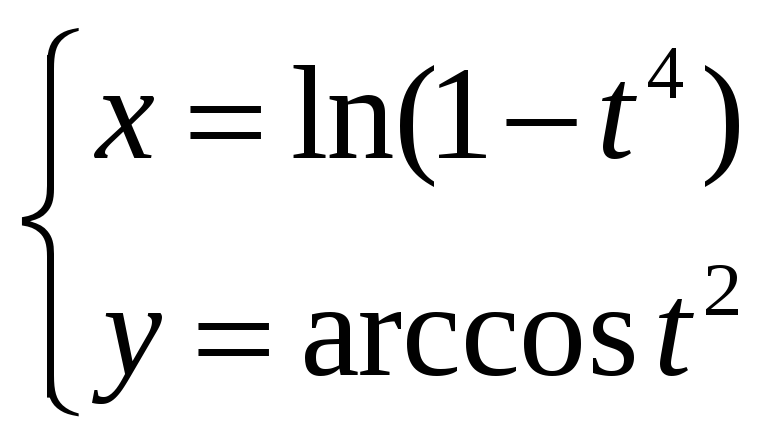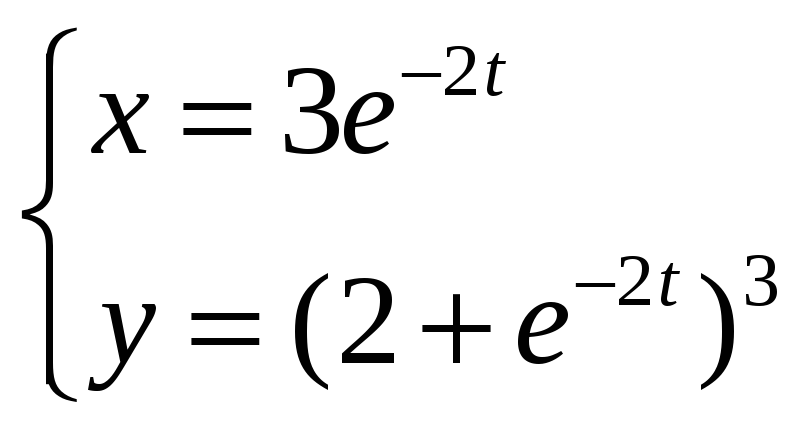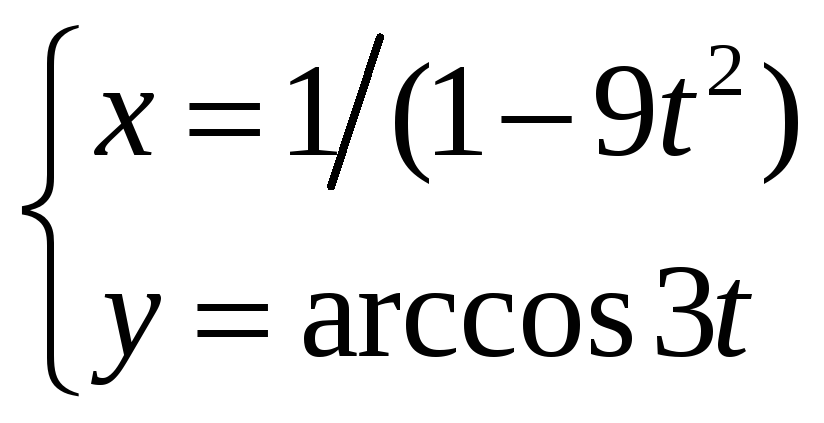Математика КР_1
.docВарианты заданий контрольной работы № 1
Задание 1. Дана
матрица
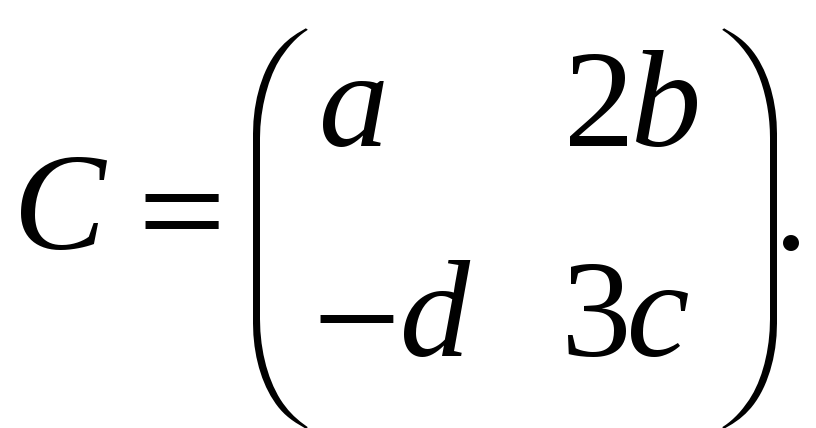
Найти матрицу
Задание 2. Дана система уравнений А·Х=В, где матрицы
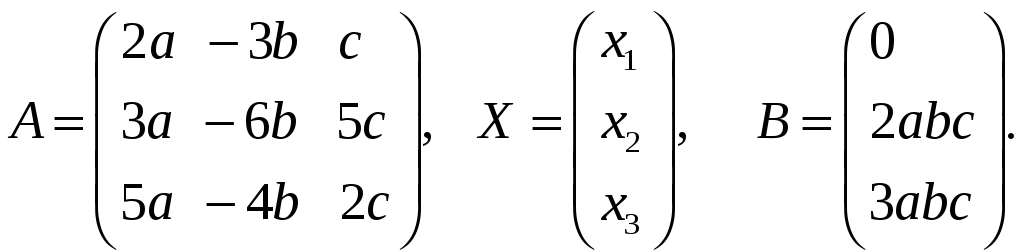
Решить систему тремя методами:
а) по формулам Крамера;
б) матричным методом;
в) методом Жордана—Гаусса.
Значения параметров а, b, c, d к заданиям 1, 2 даны в таблице.
|
Номер варианта |
a |
b |
c |
d |
Номер варианта |
a |
b |
c |
d |
|
1 |
–1 |
1 |
5 |
–4 |
11 |
1 |
2 |
–2 |
4 |
|
2 |
2 |
1 |
4 |
–1 |
12 |
1 |
3 |
–2 |
–2 |
|
3 |
1 |
–3 |
1 |
–4 |
13 |
3 |
–3 |
1 |
2 |
|
4 |
2 |
1 |
6 |
1 |
14 |
–2 |
3 |
–1 |
1 |
|
5 |
1 |
–2 |
–1 |
6 |
15 |
1 |
1 |
5 |
–2 |
|
6 |
3 |
–2 |
1 |
1 |
16 |
1 |
–2 |
3 |
–1 |
|
7 |
–1 |
1 |
3 |
–3 |
17 |
3 |
–1 |
2 |
5 |
|
8 |
–2 |
–1 |
1 |
4 |
18 |
2 |
2 |
–1 |
4 |
|
9 |
–2 |
–2 |
3 |
1 |
19 |
1 |
–1 |
–1 |
2 |
|
10 |
4 |
3 |
2 |
1 |
20 |
4 |
1 |
–1 |
2 |
Задание 3. Даны координаты вершин треугольной пирамиды А1А2А3А4 (см. табл.). Требуется найти:
а) длины ребер А1А2 и А1А3;
б) угол между ребрами А1А2 и А1А3;
в) площадь грани А1А2А3;
г) объём пирамиды;
д) уравнения прямых А1А2 и А1А3;
е) уравнения плоскостей А1А2А3 и А1А2А4;
ж) угол между плоскостями А1А2А3 и А1А2А4;
з) высоту пирамиды.
|
Номер варианта |
А1 |
А2 |
А3 |
А4 |
|
1 |
(–1, 2, 1) |
(–2, 2, 5) |
(–3, 3, 1) |
(–1, 4, 3) |
|
2 |
(–2, 1, –1) |
(–3, 1, 3) |
(–4, 2, 1) |
(–2, 3, 1) |
|
3 |
(1, 1, 2) |
(0, 1, 6) |
(–1, 2, 2) |
(1, 3, 4) |
|
4 |
(–1, –2, 1) |
(–2, –2, 5) |
(–3, –1, 1) |
(–1, 0, 3) |
|
5 |
(2, –1, 1) |
(1, –1, 5) |
(0, 0, 1) |
(2, 1, 3) |
|
6 |
(–1, 1, –2) |
(–2, 1, 2) |
(–3, 2, –2) |
(–1, 3, 0) |
|
7 |
(1, 2, 1) |
(0, 2, 5) |
(–1, 3, 1) |
(1, 4, 3) |
|
8 |
(–2, –1, 1) |
(–3, –1, 5) |
(–4, 0, 1) |
(–2, 1, 3) |
|
9 |
(1, –1, 2) |
(0, –1, 6) |
(–1, 0, 2) |
(1, 1, 4) |
|
10 |
(1, –2, 1) |
(0, –2, 5) |
(–1, –1, 1) |
(1, 0, 3) |
|
11 |
(0, 3, 2) |
(–1, 3, 6) |
(–2, 4, 2) |
(0, 5, 4) |
|
12 |
(–1, 2, 0) |
(–2, 2, 4) |
(–3, 3, 0) |
(–1, 4, 2) |
|
13 |
(2, 2, 3) |
(1, 2, 7) |
(0, 3, 3) |
(2, 4, 5) |
|
14 |
(0, –1, 2) |
(–1, –1, 6) |
(–2, 0, 2) |
(0, 1, 4) |
|
15 |
(3, 0, 2) |
(2, 0, 6) |
(1, 1, 2) |
(3, 2, 4) |
|
16 |
(0, 2, –1) |
(–1, 2, 3) |
(–2, 3, 7) |
(0, 4, 1) |
|
17 |
(2, 3, 2) |
(1, 3, 6) |
(0, 4, 2) |
(2, 5, 4) |
|
18 |
(–1, 0, 2) |
(–2, 0, 6) |
(–3, 1, 2) |
(–1, 2, 4) |
|
19 |
(2, 0, 3) |
(1, 0, 7) |
(0, 1, 3) |
(2, 2, 5) |
|
20 |
(2, –1, 2) |
(1, –1, 6) |
(0, 0, 2) |
(2, 1, 4) |
Задание 4. Найти производные 1-го порядка данных функций.
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
13 |
|
|
|
|
|
14 |
|
|
|
|
|
15 |
|
|
|
|
|
16 |
|
|
|
|
|
17 |
|
|
|
|
|
18 |
|
|
|
|
|
19 |
|
|
|
|
|
20 |
|
|
|
|
Задание 5. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
|
Номер варианта |
Вид функции f(x) |
Номер варианта |
Вид функции f(x) |
|
1 |
|
11 |
|
|
2 |
|
12 |
|
|
3 |
|
13 |
|
|
4 |
|
14 |
|
|
5 |
|
15 |
|
|
6 |
|
16 |
|
|
7 |
|
17 |
|
|
8 |
|
18 |
|
|
9 |
|
19 |
|
|
10 |
|
20 |
|
Задание
6.
Найти производную
функции y=у(x),
заданной параметрически:
|
Номер варианта |
|
Номер варианта |
|
Номер варианта |
|
||
|
1 |
|
8 |
|
15 |
|
||
|
2 |
|
9 |
|
16 |
|
||
|
3 |
|
10 |
|
17 |
|
||
|
4 |
|
11 |
|
18 |
|
||
|
5 |
|
12 |
|
19 |
|
||
|
6 |
|
13 |
|
20 |
|
||
|
7 |
|
14 |
|
|
|
||
Задание 7. Найти дифференциалы функций
|
Номер варианта |
y=f(x) |
u=u(x) |
s=s(t) |
|||
|
1 |
а) |
|
б) |
|
в) |
|
|
2 |
а) |
|
б) |
|
в) |
|
|
3 |
а) |
|
б) |
|
в) |
|
|
4 |
а) |
|
б) |
|
в) |
|
|
5 |
а) |
|
б) |
|
в) |
|
|
6 |
а) |
|
б) |
|
в) |
|
|
7 |
а) |
|
б) |
|
в) |
|
|
8 |
а) |
|
б) |
|
в) |
|
|
9 |
а) |
|
б) |
|
в) |
|
|
10 |
а) |
|
б) |
|
в) |
|
|
11 |
а) |
|
б) |
|
в) |
|
|
12 |
а) |
|
б) |
|
в) |
|
|
13 |
а) |
|
б) |
|
в) |
|
|
14 |
а) |
|
б) |
|
в) |
|
|
15 |
а) |
|
б) |
|
в) |
|
|
16 |
а) |
|
б) |
|
в) |
|
|
17 |
а) |
|
б) |
|
в) |
|
|
18 |
а) |
|
б) |
|
в) |
|
|
19 |
а) |
|
б) |
|
в) |
|
|
20 |
а) |
|
б) |
|
в) |
|
