Геометрический смысл производной. Если кривая задана уравнением , то— угловой коэффициент касательной к графику функции в этой точке ().

Уравнение касательной к кривой 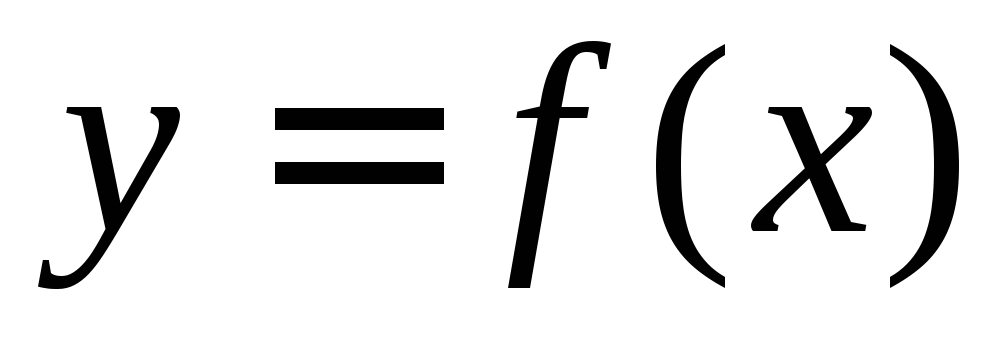в точкех₀(прямаяМ₀Т) имеет вид:

(2)

а уравнение нормали (М₀N):

(3)

Механический смысл производной. Если точка движется по закону S=s(t), где S — путь, t — время, то S (t) представляет скорость движения точки в момент времени t, т. е. S (t) =V(t).

Правила дифференцирования

№ пп	U = u(x), V=V(x) — дифференцируемые функции	№ пп	U = u(x), V=V(x) — дифференцируемые функции
I		VI	Производная сложной функции
II		VII	Функция задана параметричес-кими уравнениями
III
IV		VIII	Если и—взаимнообратные функции, то
V

Формулы дифференцирования основных элементарных функций

№ пп	с=const, х — независимая переменная, u = u(x) — диф­ференцируемая функция
1	с= 0	9
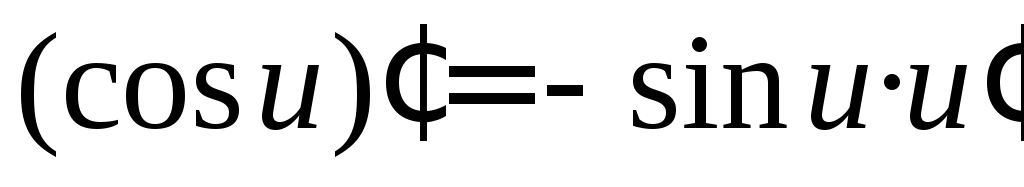
2	х= 1	10
3		11
4		12
5		13
6		14
7		15
8

Замечание. Формулы записаны с учётом правила дифференцирования сложной функции.