31

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Донской государственный технический университет

Кафедра «Прикладная математика»

Составители: доцент, к.ф.-м. н. Трепачев В.В.,

доцент, к.ф.-м. н. Нурутдинова И.Н.

Решение задач и примеров по математике

(1-й семестр обучения )

Методическое пособие

по дисциплине «Математика»,

для студентов всех специальностей,

всех форм обучения

Ростов-на-Дону

2012

УДК 510

Трепачев В. В., Нурутдинова И.Н. Решение задач и примеров по математике (1-й семестр). Ростов -на- Дону, ДГТУ, 2012, 20с.

В методическом пособии кратко изложены начальные и основные подходы для ,

решения типичных задач и примеров по математике в первом семестре обучения.

Пособие предназначено для подготовки к контрольным работам и тестированию

для студентов всех форм обучения и всех специальностей.

Содержание

1. Литература с.2

2. Введение с.2

3. Решение типовых задач и примеров по темам: с. 3–19

3.1 Линейная алгебра и аналитическая геометрия с. 3–10

3.2. Производная и пределы с. 11-14

3.3. Функции нескольких переменных с.14-19

4. Краткие сведения по теме производная функции одной переменной с.19–20

1.Литература

1.Минорский В.П. Сборник задач по высшей математике. М.: «Высш. школа», 1985, 359с.

2...Кудрявцев В. А, Демидович Б.П.. Краткий курс высшей математики. М: «Наука», 1986, 497с.

3.Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. СПб.: Изд-во «Лань»,2002,960 с.

4. Данко П. Е., Попов А. Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.

В 3-х ч. , часть1, М.: «Высш. школа», 1986, 385с.

5. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. В 2-х т.,

том 1,М: «Наука», 1978, 250с.

2. Введение.

При подготовке к экзамену по теории и практике курса математики 1 семестра следует использовать источники [1]-[5], варианты контрольных работ изложены в отдельных электронных методических пособиях, важный материл в виде сводок формул и определений по основным разделам математики можнополучить, используя задачник [1].

3.1.Пример решения к.Р. №1 по математике по теме

«Линейная алгебра и аналитическая геометрия», 1 семестр

Задача 1. Дана матрица Найти

Решение.

Через определитель и алгебраические дополнения найдем обратную матрицу:

Задача 2. Решить систему уравнений

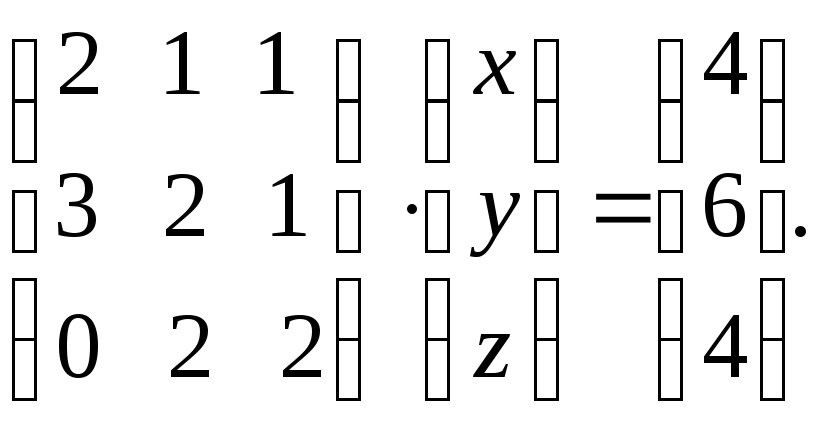
a) методом Крамера, b) матричным методом, c) методом Гаусса.

Решение. a) метод Крамера. Считаем определители разложением по первой строке (столбцы по очереди меняются на столбец свободных членов)

Теперь найдем ответ по формулам

b) матричный метод. Найдем обратную матрицу по формуле

где - алгебраическое дополнение элемента

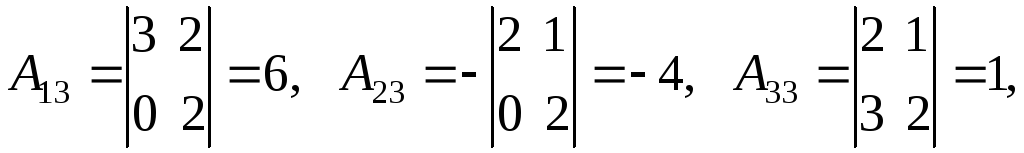
Теперь ответ найдем по формуле

c) метод Гаусса. Делаем элементарные преобразования расширенной матрицы, нумеруем строки римскими цифрами.

. Получили диагональную матрицу, начинаем решать с последнего уравнения (обратный ход):

Отметим, что во всех трех способах ответы совпали.

Задача 3. В каноническом базисе даны координаты векторов

a) Показать, что - базис вR³.

b) Записать матрицу перехода от базиса к базисуи разложить векторв этом базисе.

Решение. a) Составим определитель из координат векторов :

Определитель из координат не равен нулю, значит, эти векторы составляют базис в R³.

b) Матрица перехода от базиса к базисуимеет вид (координаты векторов записаны по столбцам)

.

Координаты вектора в базисенайдем из уравнения

или в матричной форме

Решим эту систему методом Крамера (см. задачу 2).

Задача 4. Дана матрица

1) Для системы , гдеX – 5-мерный вектор-столбец неизвестных

найти

a) фундаментальную систему решений,

b) общее решение,

c) частное решение.

2) Пусть C – расширенная матрица системы 4-х уравнений с 4-мя неизвестными. Решить эту систему, исследовав совместность по теореме Кронекера-Капелли.

Решение. 1) Решим систему методом Гаусса, совершая элементарные преобразования строк, нумеруя строки римскими цифрами, обнуляем элементы ниже диагонали.

Пусть x₅ – свободное неизвестное. Последнее уравнение имеет вид

из третьего уравнения найдем

из второго уравнения найдем

из первого уравнения найдем

a) Общее решение имеет вид (x₅ – свободное неизвестное):

b) Частное решение найдем, положив x₅=1:

c) Отсюда фундаментальное решение запишем в виде

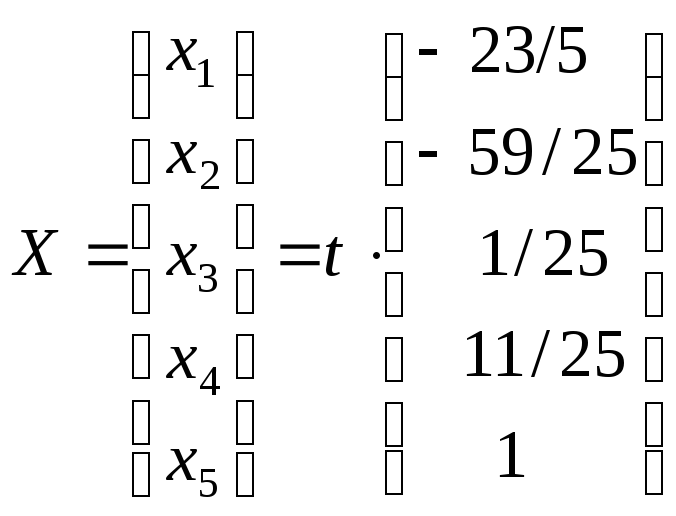. Здесь t – любое число.

2) Ранг основной матрицы равен 4 и совпадает с рангом расширенной матрицы, поэтому система совместна по теореме Кронекера-Капелли.

Расширенная матрица уже приведена к виду (см. выше)

Совершая обратный ход (начиная с последнего уравнения), последовательно найдем: из четвертого уравнения

из третьего уравнения

из второго уравнения

из первого уравнения

Задача 5. Даны четыре точки – вершины пирамиды с координатами

Найти:

а)

б) угол между ребрами

в) площадь грани

г) объем пирамиды;

д) уравнения прямых

е) уравнения плоскостей

ж) угол между плоскостями

з) высоту пирамиды как расстояние от точки A₄ до плоскости

Решение.

а)

б)

в) Искомая площадь S равна половине модуля векторного произведения векторов:

,

г) Искомый объем V равен одной шестой модуля смешанного произведения векторов:

,

д) Каноническое уравнение прямой

Каноническое уравнение прямой

е) Уравнение плоскости найдем как смешанное произведение векторов (M(x,y,z) – текущая точка плоскости)

Уравнение плоскости найдем как смешанное произведение векторов (M(x,y,z) – текущая точка плоскости)

ж) Угол между плоскостями равен углу между нормалями к этим плоскостям. Из пункта е) видно, что для плоскости нормаль

а для плоскости нормальзначит, косинус угла между этими плоскостями равен

з) Высота пирамиды h вычисляется через ее объем V (см. пункт г)) и площадь основания S (см. пункт в)) по формуле

Пример решения К.Р. 1 математике по теме

«Производная и пределы», 1 семестр

Задача 1. Найти производные

Решение. Пользуясь таблицей и правилами дифференцирования, найдем

Задача 2. Написать уравнения касательной и нормали к кривой

в точке x₀=1.

Решение. Уравнение касательной имеет вид

Отсюда

уравнение касательной

Уравнение нормали имеет вид

Отсюда искомое уравнение

Задача 3. Найти производную функции, заданной параметрически в виде

Решение. Дифференцируя найдем

Задача 4. Найти дифференциал функции

Решение. Дифференциал функции y(x) равен dy=y’dx. Значит,

Задача 5. Найти вторую производную функции

Решение. Пользуясь таблицей и правилами дифференцирования, найдем

Задача 6. Найти скорость и ускорение точки при t=2, если ее путь задан функцией

Решение. Скорость - это первая производная, а ускорение - вторая производная.

Задача 7. Найти пределы

Решение. a) Делим числитель и знаменатель на старшую степень x:

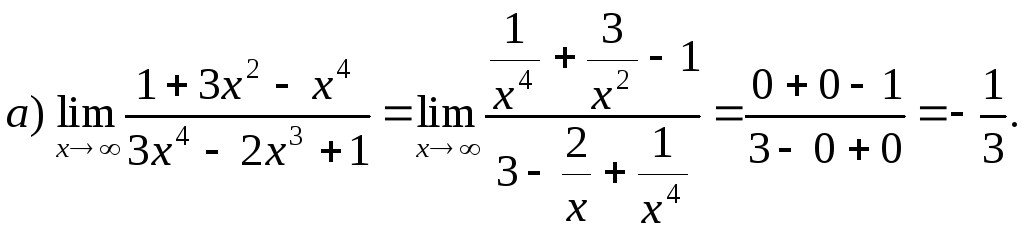
b) Разложим числитель и знаменатель на множители и сократим дробь:

c) Bоспользуемся правилом Лопиталя раскрытия неопределенности:

Задача 8. Исследовать функцию на экстремум, выпуклость и перегиб

Решение. Найдем производную, ее нули (критические точки)

При возрастании x производная в точке меняет знак с плюса на минус (функция после возрастания начинает убывать), значит,- это точка максимума функции,

При возрастании x производная в точке меняет знак с минуса на плюс (функция после убывания начинает возрастать), значит,- это точка минимума функции,