
Термодинамика-621.Т35
.pdfнии полного равновесия за счет односторонне протекающих в природе процессов, после чего прекращаются всякие тепловые процессы и наступает «тепловая смерть».
Ошибочность его концепций состояла в том, что он принимал Вселенную в качестве конечной изолированной системы, в то время как она бесконечна.
Циклы двигателей внутреннего сгорания
Двигателями внутреннего сгорания (ДВС) называются тепловые двигатели, рабочим телом которых служат газообразные продукты сгорания топлива, сжигаемого непосредственно внутри самого двигателя. Чаще всего это название относится к поршневым ДВС.
В настоящее время существует множество различных типов, видов и конструкций ДВС, отличающихся друг от друга по всевозможным признакам (скорость сгорания топлива, способ смесеобразования, тип продувки, быстроходность, архитектурная схема расположения цилиндров и т.д.). Все поршневые двигатели можно разбить на две основные группы: низкого и высокого сжатия.
К двигателям низкого сжатия относятся карбюраторные и газовые. Отличительной особенностью этой группы является то, что сжатию в цилиндре подвергается смесь паров топлива с воздухом (горючая смесь). Если считать процесс 1 – 2 адиабатным, то температура в конце сжатия Т2 определяется выражением:
|
= T1 |
|
v |
k−1 |
|
|
T2 |
|
1 |
|
, |
(0.16) |
|
|
||||||
|
|
v2 |
|
|
|
|
где v1 / v2 = ε – степень сжатия рабочего тела в цилиндре.
Так как эта температура не должна достигать в таких двигателях температуры самовоспламенения горючей смеси, то степень сжатия в них относительно невелика: ε = 5 – 8.
Другой характерной чертой таких ДВС является то, что зажигание рабочей смеси в них осуществляется от постороннего источника (чаще всего от искры электрического разряда). Нагретая в конце процесса сжатия горючая смесь, воспламенившись от искры, сгорает сравнительно быстро, при этом объем камеры сгорания между поршнем и головкой цилиндра почти не изме-
няется. Можно считать, что подвод тепла к рабочему телу осуществляется при
v = const.
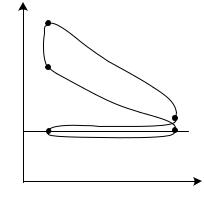
Диаграмма изменения давления в цилиндре двигателя за цикл снимается с помо-
щью специального прибора – индикатора и называется индикаторной диаграммой. Линия 0 – 1 индикаторной диаграммы карбюратор-
ного четырехтактного двигателя (рис. 3.8) отражает такт всасывания, происходящий при давлении несколько меньшем, чем атмосферное.
Далее идет процесс сжатия рабочей
Рис. 0.8
смеси 1 – 2 по линии, приближающейся к адиабате, затем сгорание топлива 2 – 3, про-
текающее вблизи v = const. Под давлением продуктов сгорания поршень совершает рабочий ход, отражаемый на диаграмме процессом расширения 3 – 4. Такт выхлопа 4 – 0 замыкает рабочий процесс. Впервые двигатель со сжатием горючей смеси и воспламенением топлива от искрового разряда с последующим быстрым сгоранием был построен немецким изобретателем Отто в 1876 г.
Для термодинамического анализа удобнее рассматривать идеализированный цикл Отто, сохраняющий принципиальные черты действительного цикла. Переходя от реального цикла к термодинамическому, делают следующие допущения:
1)исключаются насосные ходы поршня (процессы всасывания воздуха
ивытеснения газов);
2)цикл считается замкнутым, в нем участвует постоянное рабочее тело в количестве 1 кг;
3)состав рабочего тела не изменяется за время цикла, причем рабочее тело обладает свойствами идеального газа;
4)процессы сжатия рабочего тела 1 – 2 и расширения 3 – 4 осуществляются адиабатно;
5)процессы подвода и отвода тепла осуществляются по изохорам
2 – 3 и 4 – 1.
Р |
3 |
|
|
|
T |
q1 |
3 |
|
|
|
|
|
|
|
|
|
q1 |
|
v=const |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
q |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
q2 |
1 |
q2 |
|
|
|
|
|
|
|
|
|
|
pv |
k |
=const |
1 |
|
|
|
|
|
|
|
|
|
||
|
v2=v3 |
|
v1=v4 v |
S1=S2 |
|
S3=S4 S |
|
|
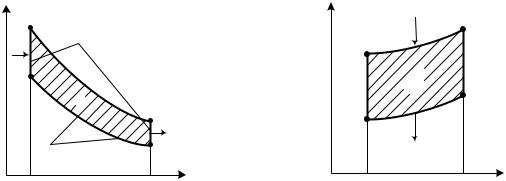
Рис. 0.9 |
|
Рис. 0.10 |
|
|||
Таким образом, термодинамический цикл Отто состоит из двух изохор и двух адиабат (рис. 3.9). Площадь, ограниченная контурами цикла, представляет собой величину полезной работы цикла. В диаграмме T, s этот цикл имеет вид, показанный на рис. 3.10.
Термический КПД цикла с подводом тепла при v = const определяется из общего для всех циклов выраженияηt = 1 − q2  q1 , если в него подставить значения отведенного в процессе 4 – 1 тепла q2 = cv(T4 – T 1) и подведенного в изохорном процессе 2 – 3 тепла q1 = cv(T3 – T 2):
q1 , если в него подставить значения отведенного в процессе 4 – 1 тепла q2 = cv(T4 – T 1) и подведенного в изохорном процессе 2 – 3 тепла q1 = cv(T3 – T 2):
ηt |
= 1 − |
cv (T4 |
− T1 ) |
. |
(0.17) |
|
cv (T3 |
− T2 ) |
|||||
|
|
|
|
Считая сv = const, преобразуем выражение (3.17) к виду:
η |
t |
= 1 − |
T4 / T1 |
−1 |
|
T1 |
. |
(0.18) |
|
|
|
|
|||||||
|
|
T3 |
/ T2 |
−1 T2 |
|
||||
|
|
|
|
||||||
Из адиабаты 1 – 2 имеем:
T |
v |
2 |
k−1 |
|
|||
1 |
= |
|
|
, |
(0.19) |
||
T2 |
v1 |
||||||
|
|
|
|
||||
а из адиабаты 3 – 4:
T |
v |
3 |
k-1 |
|
|
4 |
= |
|
. |
(0.20) |
|
T3 |
|
|
|||
v4 |
|
|
|||
Правые части выражений (3.19) и (3.20) равны, поэтому T1 / T2 = T4 / T3,
T4 |
= |
T3 |
. |
(0.21) |
T3 |
|
|||
|
T2 |
|
||
Подставляя соотношение (3.21) в формулу (3.18), получаем
ηt |
= 1 − T1 / T2 , |
(0.22) |
|
или, с учетом выражения (3.18) (зная, что v1 / v2 = ε): |
|
||
η |
t |
= 1 −1/ εk−1 . |
(0.23) |
|
|
|
|
Из формулы (3.23) видно, что термический КПД цикла ДВС с подводом тепла при постоянном объеме зависит только от степени сжатия ε, с увеличением которой ηt возрастает.
Существенного повышения ε добиваются в двигателях высокого сжатия, в которых сжимается не горючая смесь, а чистый воздух. Температура конца процесса сжатия должна превышать температуру воспламенения топлива, впрыскиваемого в камеру сгорания, так как двигатель работает без постороннего источника зажигания, за счет самовоспламенения паров топлива.
Степень сжатия ε при этом у современных |
|
двигателей достигает 12 – 20. |
|
По имени немецкого инженера Р. Дизе- |
|
ля, построившего в 1897 г. двигатель, работа- |
|
ющий по этому принципу, двигатели внут- |
|
реннего сгорания высокого сжатия иногда |
|
называются дизелями. |
|
В первых дизелях с целью улучшения |
|
распыливания топлива использовался сжатый |
|
воздух. Привод компрессора осуществлялся |
|
от вала двигателя, расходуя значительную |
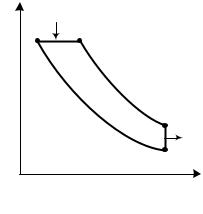
Рис. 0.11 |
часть его мощности. Применение форсунок с |
|
воздушным распыливанием позволяет так отрегулировать процесс горения при одновременном увеличении камеры сгорания, что он протекает практически при постоянном давлении: р = const. В остальном цикл Дизеля (рис. 3.11) аналогичен рассмотренному ранее циклу Отто.
Термический КПД цикла с изобарным подводом тепла
ηt |
= 1 − |
q2 |
= 1 − |
cv (T4 − T1 ) |
= 1 − |
T1 |
|
T4 / T1 −1 |
. |
(0.24) |
q1 |
cp (T3 − T2 ) |
T2 |
|
|||||||
|
|
|
|
|
k(T3 / T2 ) −1 |
|
||||
В изобарном процессе подвода тепла 2 – 3 происходит некоторое увеличение объема до начала адиабатного процесса расширения 3 – 4, поэтому для характеристики цикла Дизеля вводится показатель – степень предварительного расширения
|
|
|
|
ρ = |
v3 |
= |
T3 |
. |
|
|
|
(0.25) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
v2 |
|
|
|
T2 |
|
|
|
|
||||||
Отношение температур T4 / T1 также можно выразить через ρ, восполь- |
||||||||||||||||||||||
зовавшись уравнениями 4 – 3 и 1 – 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p |
4 |
vk |
= p |
vk |
; p vk = p |
2 |
vk . |
|||||||||||||||
|
4 |
|
|
3 |
3 |
|
|
|
1 |
1 |
|
|
|
2 |
||||||||
Так как v4 = v1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
p |
4 |
|
|
|
|
p |
3 |
vk |
|
|
|
|
|||||||
|
|
4 |
|
= |
|
= |
|
|
|
|
|
3 |
= ρk . |
(0.26) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
T1 |
|
p1 |
|
|
|
|
p2 v2k |
|
|
|
|
||||||||||
После подстановки связей (3.19), (3.25) и (3.26) в уравнение (3.24) |
||||||||||||||||||||||
окончательно получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ηt |
= 1 − |
1 |
|
|
|
|
|
ρk −1 |
. |
(0.27) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
εk−1 k(ρ −1) |
|
|
||||||||||||
Термический КПД с ростом ε, как и в цикле Отто, увеличивается, а с ростом ρ, что соответствует увеличению нагрузки на двигатель, падает.
К 1904 г. относят изобретение двигателя Тринклера, который запатентовал форсунку, способную распыливать топливо без помощи сжатого воздуха. Плунжерным насосом создается высокое давление топлива (до 150 – 200 МПа), за счет чего осуществляется механическое его распыливание при впрыске в ка-
меру сгорания. Горение топлива при этом происходит в две стадии. Вследствие периода задержки воспламе-
нения топлива происходит его накопление и испарение. Образовавшаяся горючая смесь по-
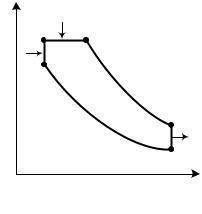
Рис. 0.12
сле самовоспламенения сгорает почти мгновенно. Эта стадия горения соответствует изохорному участку 2 – z подвода тепла q1v в термодинамическом цикле двигателя Тринклера (рис. 3.12). Сгорание остальной части топлива происходит постепенно по мере поступления его из форсунки. На диаграмме p, v это отражается изобарным участком подвода тепла q1p в процессе z – 3.
Такой характер горения топлива свойственен большинству современных бескомпрессорных дизелей.
Термический КПД цикла со смешанным подводом тепла
|
|
|
|
|
|
|
ηt =1 − |
|
q2 |
=1 − |
|
|
|
|
|
|
cv (T4 − T1 ) |
= |
|
|||||||||
|
|
|
|
|
|
|
q1v + q1p |
|
cv (Tz − T2 ) + cp (T3 − Tz ) |
(0.28) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
T1 |
|
|
|
|
|
|
|
T4 / T1 −1 |
|
|
|
||||||||
|
|
|
|
|
|
|
=1 − |
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
T2 |
|
(Tz / T2 −1) + k(T3 / T2 − Tz / T2 ) |
|
|
|||||||||||||||
|
|
|
Выразим отношение температур в уравнении (3.28) через характери- |
|||||||||||||||||||||||||
стики ДВС ε, λ, ρ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Для |
изохоры |
4 |
– |
|
1, используя |
|
уравнения адиабат 4 – 3 |
и 1 – 2: |
|||||||||||||||||
p |
4 |
vk |
= p |
vk |
; p vk = p |
2 |
vk |
, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 |
3 |
|
3 |
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
p |
4 |
|
p |
3 |
v |
3 |
k |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
= |
|
|
= |
|
|
|
|
= λρk , |
|
(0.29) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
p2 v2 |
|
|
|
||||||||||
где λ = р3 / р2 – степень повышения давления в процессе изоxoрного подвода тепла. Для изохоры 2 – z
Tz |
= |
pz |
= λ . |
(0.30) |
|
|
|||
T2 |
|
p2 |
|
|
Поскольку T3 / Tz = v3 / vz = ρ, то
T3 |
= |
T3 |
|
Tz |
= λρ . |
(0.31) |
T2 |
Tz |
|
T2 |
|||
|
|
|
|
Подставив в уравнение (3.28) вместо отношений температур их значения, получаем
η = 1 − |
1 |
|
λρk −1 |
. |
(0.32) |
εk−1 |
|
(λ −1) + kλ(ρ −1) |
|||
t |
|
|
|
||
|
|
|
|
|
Формула термического КПД смешанного цикла имеет в известной мере |
||
обобщающее значение, так как из нее могут быть получены выражения ηt |
||
циклов Отто и Дизеля. Действительно, в цикле Отто отсутствует изобарный |
||
участок подвода тепла, а все тепло подводится при v = const. Это условие вы- |
||
держивается, если в смешанном цикле положить ρ = 1. Тогда формула (3.32) |
||
трансформируется в (3.23). В цикле Дизеля нет изохорного участка, т. е. λ = |
||
1. Подставляя это условие в уравнение (3.32), получим формулу (3.27) тер- |
||
мического КПД цикла с подводом тепла при р = const. |
||
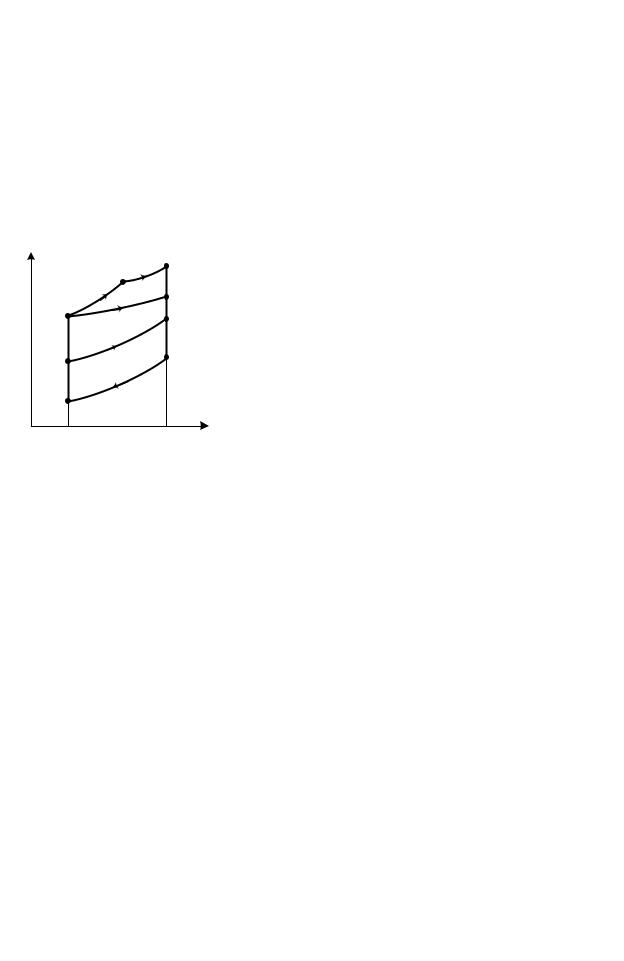
|
Для решения вопроса о целесообразности |
|
|
использования того или иного цикла ДВС про- |
|
|
ведем их термодинамическое сравнение в Т, s- |
|
|
диаграмме (рис. 3.13). Будем считать, что отве- |
|
|
денное тепло q2 во всех случаях одинаково. |
|
|
Степень сжатия ε в смешанном Цикле и в цикле |
|
|
Дизеля существенно выше, чем в цикле с изо- |
|
|
хорным подводом тепла. Поэтому точка 2v рас- |
|
|
положится на адиабате сжатия много ниже, чем |
|
Рис. 0.13 |
точка 2p и 2см (которые можно совместить, так |
|
как ε в циклах Дизеля и Тринклера примерно |
||
|
||
одинаковы). Точки конца процесса подвода тепла 3v, 3р, 3см получаются из |
||
построения |
процессов |
|
v = const, p = const и смешанного. |
||
При равных значениях q2 величина термического КПД ηt = 1 – q 2 / q1 |
||
будет определяться значением q1. Как видно из диаграммы (см. рис. 3.13), |
||
q1см > q1p > q1v, поэтому ηt см > ηt p > ηt v. |
||
Сравнение циклов показывает, что термический КПД бескомпрессор- |
||
ных дизелей имеет наибольшее значение, поэтому они широко применяются |
||
в качестве стационарных и судовых установок, а также в тяжелых транс- |
||
портных средствах – |
тепловозах, самосвалах. Двигатели же низкого сжатия, в |
|
частности бензиновые карбюраторные ДВС, работают с наименьшим КПД. |
||
Тем не менее они имеют большое распространение (в силу малого веса) в ав- |
||
томобильном транспорте и в других случаях, когда бывает необходимость в |
||
легком |
|
|
двигателе. |
|
|
Что касается компрессорных дизелей, работающих по циклу с подво- |
||
дом тепла при р = const, то в настоящее время они не применяются, так как |
||
имеют низкий эффективный КПД из-за больших потерь мощности на привод компрессора для сжатия воздуха.
Циклы газотурбинных установок
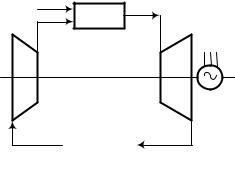
Газотурбинная установка (ГТУ) представляет собой тепловой двигатель, основным элементом которого является газовая турбина. Кроме того, в схему простейшей ГТУ (рис. 3.14) входят камера сгорания и воздушный компрессор.
Принцип работы такого теплового двигателя состоит в следующем. Наружный
воздух сжимается в компрессоре и подается в камеру сгорания, куда одновременно по-
дается и топливо. Образующиеся продукты сгорания направляются в газовую турбину, где, расширяясь до давления окружающей среды, производят работу и выбрасываются наружу. Механическая энергия, выработан-
ная в газовой турбине, с помощью генератора превращается в электрическую.
Процесс горения в камере сгорания может быть организован двумя различными путями: при постоянном давлении (p = const) и постоянном объеме
(v = const).
В первом типе ГТУ процессы подачи топлива и воздуха, а также горения и истечения осуществляются непрерывно.
Для осуществления сгорания топлива при v = const во втором типе установок камеру сгорания после наполнения ее горючей смесью необходимо отключать, закрывая впускные и выпускные клапаны.
Затем производится зажигание рабочей смеси искровым электрическим разрядом, ее горение при постоянном объеме, после чего продукты сгорания выпускаются из камеры в газовую турбину. Для снижения пульсации давления ставят несколько камер сгорания на одну турбину.
Рассмотрим идеализированные термодинамические циклы газотурбинных установок. Цикл с подводом тепла при р = const (рис. 3.15) состоит из адиабаты 1 – 2 сжатия воздуха в компрессоре, процесса 2 – 3 изобарного
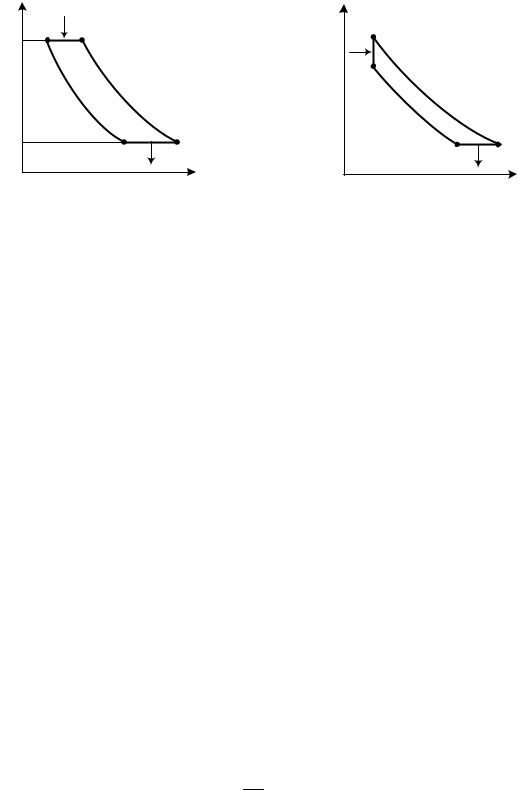
подвода тепла q1, адиабаты 3 – 4 расширения газов в проточной части турбины и изобары 4 – 1 отвода тепла q2.
Рис. 0.15 |
Рис. 0.16 |
Термический КПД цикла определяется по общей формуле:
|
q |
2 |
|
|
cp (T4 |
− T1 ) |
|
|
|
|
T T / T −1 |
|
|||||||||
ηt =1 − |
|
=1 − |
|
|
|
|
|
|
|
|
|
=1 − |
1 |
|
4 1 |
. |
(0.33) |
||||
q1 |
cp (T3 − T2 ) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
T2 T3 / T2 −1 |
|
|||||||||||||
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
k−1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
T |
|
k |
|
|
|
T |
|
|
|
|
|
||||||
|
|
|
|
1 |
= |
1 |
|
|
|
|
|
= |
4 |
, |
|
|
|
|
|||
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
p2 |
|
|
|
|
|
|
|
T3 |
|
|
|
|
|
||||
то T4 / T2 = T3 / T2 и запись формулы (3.33) приобретает вид: |
|
||||||||||||||||||||
|
|
|
|
|
η |
t |
=1 − |
T1 |
. |
|
|
|
|
|
|
(0.34) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обозначив степень повышения давления в компрессоре p2 / p1 = σ, а степень сжатия, как и прежде, v1 / v2 = ε, получаем окончательное выражение для термического КПД цикла ГТУ с подводом тепла при постоянном давле-
нии: |
|
|
|
|
|
|
η =1 − |
1 |
=1 − |
1 |
. |
(0.35) |
|
k−1 |
|
|||||
|
t |
|
εk−1 |
|
||
|
|
|
|
|
|
|
σ k
Термический цикл газотурбинной установки с подводом тепла при v = const отличается от предыдущего лишь процессом 2 – 3 ( рис. 3.16).

Найдем термический КПД этого цикла:
|
|
|
|
|
|
|
q |
2 |
|
|
|
cp (T4 − T1 ) |
|
|
T T / T −1 |
|
|
|
|
||||||||||
|
|
|
|
η |
t |
=1 − |
|
=1 |
− |
|
|
|
|
|
|
|
= |
1 − k |
1 |
|
|
4 1 |
. |
|
|
(0.36) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
q1 |
|
|
|
cv (T3 − T2 ) |
|
|
T2 T3 / T2 −1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Для изохоры 2 – 3 T 3 / T2 = p3 / p2 = λ. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Для |
изобары 4 |
– |
|
1, |
используя |
|
уравнение |
адиабат: p |
4 |
vk |
= p |
vk ; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
3 |
|
p vk = p |
2 |
vk |
, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
v |
4 |
p |
3 |
1/ k |
= λ1/ k . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
= |
|
|
= |
|
|
|
|
|
|
|
(0.37) |
|||||||
|
|
|
|
|
|
|
|
|
|
T1 |
|
v1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
После подстановки полученных выражений для отношений температур в уравнение (3.36) имеем:
η =1 − k |
1 |
|
λ1/ k −1 |
=1 − |
k |
|
λ1/ k −1 |
. |
(0.38) |
εk−1 |
|
|
|
||||||
t |
|
λ −1 |
k−1 λ −1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
σ k
Проведем сравнение циклов ГТУ с помощью Т, s-диаграммы, считая q2 = idem (рис. 3.17).
Если принять одинаковыми степени сжатия, то точка 2 будет общей для обоих циклов. Так как процесс v = const протекает круче, чем р = const, то при изохорном подводе тепла работа цикла будет больше, поэтому ηt v > ηt
p.
Если сравнить циклы из условия равенства максимальных температур конца процесса горения T3 = idem, тогда совместятся точки 3. Как видно из диаграммы на рис. 3.18, в этом случае КПД цикла с изобарным подводом тепла будет больше, т.е. ηt p > ηt v.
