3.5. Определение ускорений точек механизма методом планов ускорений

Значения и направления ускорений точек механизма необходимо знать для определения значений и направлений сил инерции звеньев и угловых ускорений. При помощи планов ускорений можно вычислить ускорения любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться свойствами планов ускорений, которые такие же, как и у планов скоростей (см. подразд. 3.4), кроме третьего, где фигура, подобная одноименной жесткой фигуре на плане положений механизма, повернута на угол (180° arctg ) в сторону мгновенного ускорения ε данного звена.

Так как полные относительные ускорения состоят из геометрической суммы нормальных и тангенциальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими обозначению точек на механизме.

Определение ускорений рассмотрим на примере механизма, представленного на рис. 3.1, а.

Считая известными ускорения шарнирных точек ( ), помещаем эти точки на плане ускорений в полюсе Р_а. Звено О₁А вращается равномерно, поэтому точка А имеет только нормальное ускорение которое направлено по звену О₁А к центру вращения О₁ (см. рис. 3.1, в). Значение нормального ускорения вычисляем по формуле, м/с²:

= (3.11)

Произвольно принимаем длину отрезка , изображающего вектор ускорения (в пределах 80  100 мм, чтобы чертеж был четким). Масштабный коэффициент ускорения вычисляем по формуле, м/с²∙мм^–1:

. (3.12)

Из полюса Р_а плана, откладываем вектор параллельно звену О₁А в направлении от точки А к точке О₁.

Рассматривая движения точки В со звеньями АВ и ВО₂, составляем векторные уравнения для определения ускорения точки В:

; (3.13)

. (3.14)

В этих уравнениях известны значение ускорения и его направление, ускорение = 0 (опора). Определяем значения нормального ускорения точки В относительно А на звене АВ и точки В относительно О₂ на звене ВО₂, м/с²:

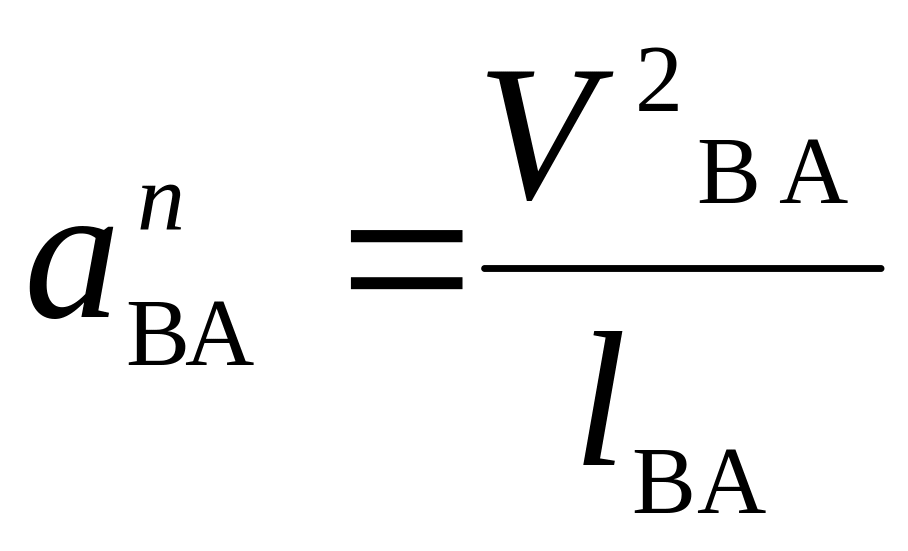; (3.15) . (3.16)

Ускорение направлено по оси звена ВА от точки В к точке А, ускорение  от точки В к точке О₂ по оси звена ВО₂. На плане ускорений ускорения и можно выразить отрезками, длина которых определяется с помощью масштабного коэффициента, мм:

; (3.17) . (3.18)

От точки а на плане ускорений параллельно звену АВ откладываем вектор , через его конец проводим перпендикулярно к звену АВ линию действия тангенциального ускорения (пунктиром). По аналогии строим вектор . Из полюса Р_а (О₁О₂) параллельно звену ВО₂ откладываем вектор , через его конец проводим перпендикулярно к звену ВО₂ линию действия тангенциального ускорения (пунктиром). При пересечении линий действия тангенциальных ускорений получим точку в. Просуммировав графически нормальное и тангенциальное ускорения, получаем векторы полных относительных ускорений – и (рис. 3.1, в).

Используя свойство подобия плана ускорений, находим места положений точек s₂ и s₃, соединяем их с полюсом плана ускорений. Затем с помощью масштабного коэффициента вычисляем значения ускорений всех точек механизма, м/с²:

; (3.19)	; (3.20)
; (3.21)	; (3.22)
; (3.23)	. (3.24)

Определяем значения и направления угловых ускорений звеньев 2 и 3, с^–2:

; (3.25) . (3.26)

Угловое ускорение кривошипа О₁А равно нулю, так как он совершает равномерное движение.

Для определения направления углового ускорения ε₂ звена АВ надо мысленно перенести вектор тангенциального ускорения в точку В звена АВ. В направлении этого вектора точка В вращается относительно точки А против хода часовой стрелки. Для определения направления углового ускорения ε₃ звена ВО₂ вектор тангенциального ускорения следует мысленно перенести в точку В звена 3. Угловое ускорение ε₃ направлено против хода часовой стрелки.

Если в механизме имеются звенья, совершающие поступательное движение (ползуны), то их угловая скорость ω, с^–1 и угловое ускорение ε, с^–2, равны нулю.