Лекция 2. ТММ

Лекция 2. ТММ

1. Схема образования механизмов по Ассуру-Артоболевскому

При проектировании новых механизмов перед конструктором ставится задача создать многозвенный механизм с уже заданным числом степеней свободы, чаще всего с W = 1; W = 2.

Впервые основной принцип образования механизмов был сформулирован в 1914 г. Л. В. Ассуром: любой плоский механизм можно создать, присоединяя к ведущему звену (или звеньям) группу звеньев с нулевой степенью подвижности (W_гр = 0) относительно тех звеньев, к которым группа присоединяется.

Кинематическая цепь с W = 0 относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающаяся на более простые цепи, имеющие также W = 0, принято называть группой Ассура.

Входящие в состав плоского механизма высшие кинематические пары IV и V классов могут быть заменены кинематическими цепями, образованными только парами V класса

Поэтому при исследовании механизмов условие, которому должны удовлетворять группы, можно записать так:

откуда

. (1.8)

Числа звеньев и пар могут быть только целыми. Уравнению (1.8) удовлетворяют следующие сочетания чисел звеньев п и число пар пятого класса р₅ (табл. 1.3).

Таблица 1.3

Зависимость чисел звеньев и кинематических пар

№ п/п	1	2	3	4	5
Число звеньев, п	2	4	6	8	…
Число кинематических пар, р5	3	6	9	12	…

Простейшее сочетание чисел звеньев и пар, удовлетворяющее уравнению (1.8), будет п = 2 (АВ, ВС); р₅ = 3 (А, В, С – вращательные) (рис. 1.12, а) и п = 2 (АВ, ползун); р₅ = 3 (А, В, ползун со стойкой) (рис. 1.12, б). Эти группы Ассура называются группами II класса. Если механизм состоит из ведущего звена и одной (или нескольких) групп II класса, то такой механизм тоже II класса. Обычно на схемах звенья обозначают арабскими цифрами, а кинематические пары – римскими.

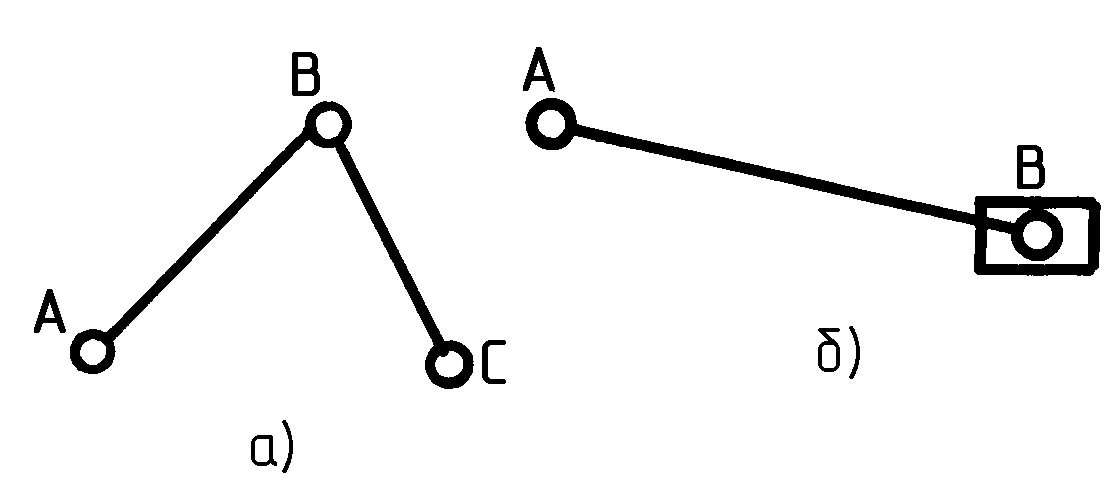
Рис. 1.12

Рассмотрим примеры.

1. В данном механизме (рис. 1.13) п = 3 (1, 2, 3); р₅ = 4 (I, II, III, IV – вращательные).

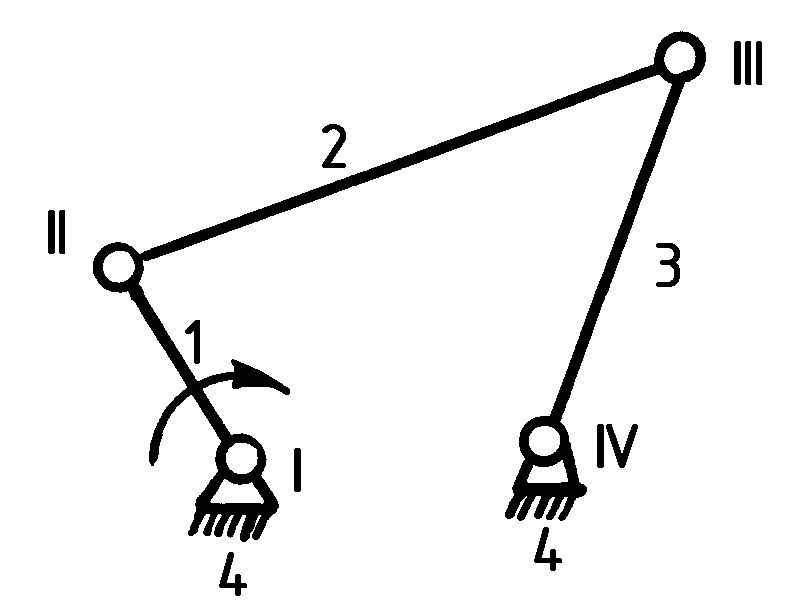
Рис. 1.13

Механизм имеет одно ведущее звено (1) и одно группу Ассура II класса (2, 3). Весь механизм II класса: [1] → [2, 3]. Ведущее звено обозначается круговой стрелкой.

2. На рис. 1.14 п = 5 (1, 2, 3, 4, 5); р₅ = 7 (I, II, III, IV, V, VI – вращательные; VII – поступательная).

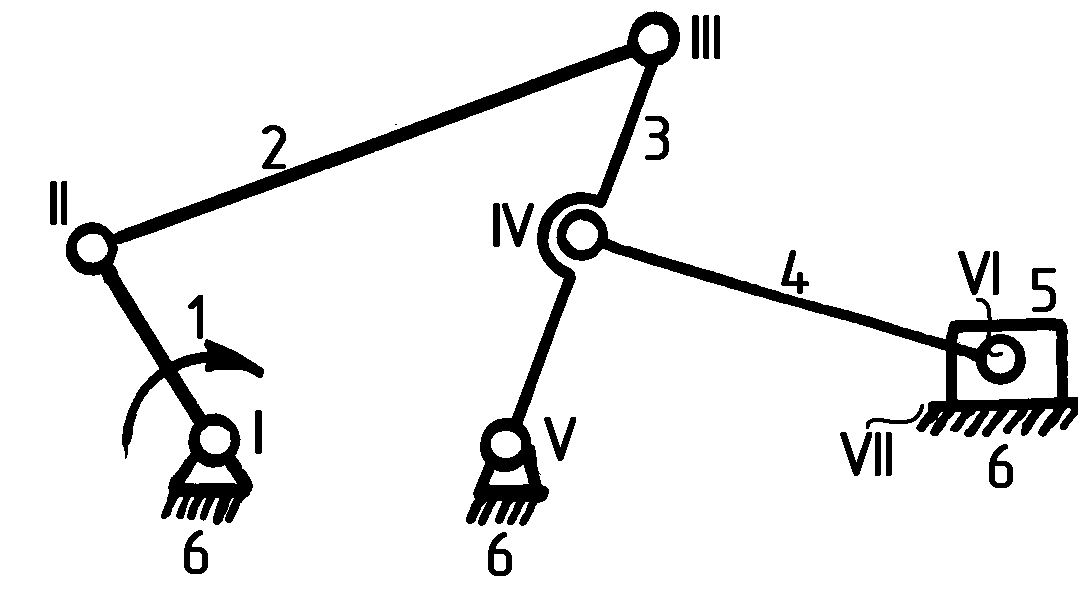
Рис. 1.14

Механизм имеет одно ведущее звено (1) и две группы Ассура II класса (2, 3; 4, 5). Весь механизм II класса: [1] → [2, 3] → [4, 5].

Возьмем еще одно сочетание чисел звеньев и кинематических пар: п = 4; р₅ = 6 (рис. 1.15).

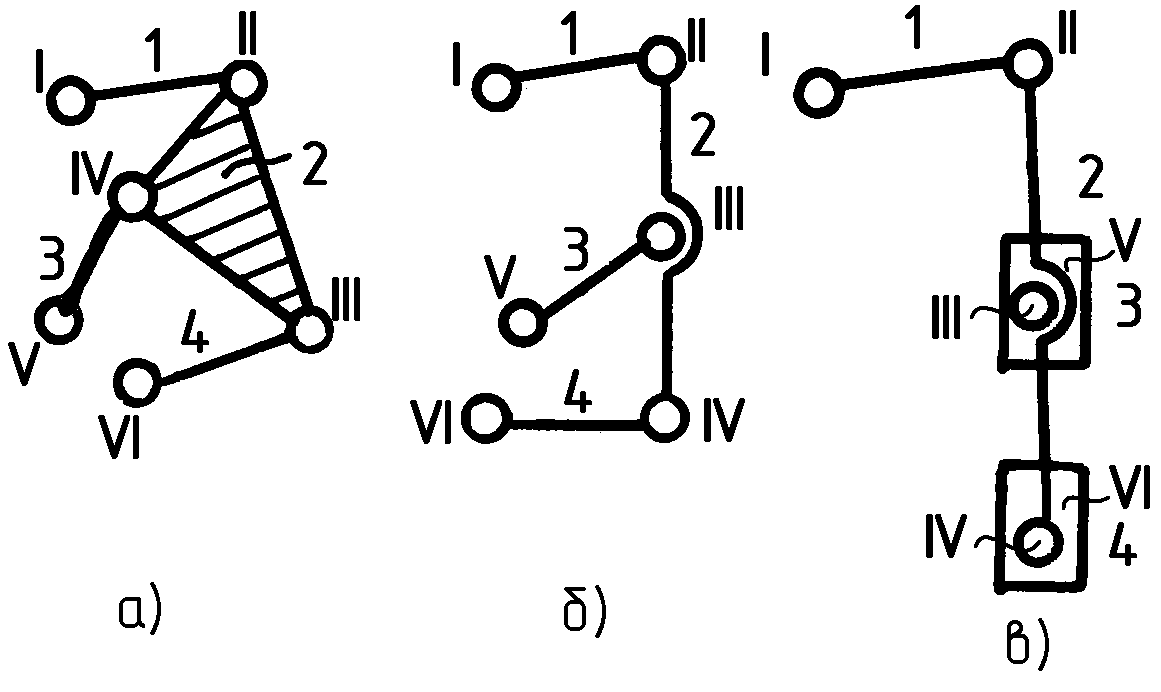
Рис. 1.15

Все три кинематические цепи имеют в своем составе одно базисное звено 2, которое может соединяться с другими звеньями для образования механизма при помощи поводков 1, 3, 4 (см. рис. 1.15, а, б) или при помощи поводка 1 и двух ползунов 3, 4 (см. рис. 1.15, в). Количество и расположение ползунов, выполняющих роль поводков, может быть разным в зависимости от вида механизма, в который данная группа Ассура входит. Такого вида цепи относятся к группам Ассура III класса. Если в механизме имеются группы II и III класса, то сам механизм считается механизмом III класса.

Примеры:

1) На рис. 1.16, а изображен механизм, который состоит из ведущего звена и группы Ассура III класса. [5] → [1, 2, 3, 4]. Значит данный механизм III класса. В его составе п = 5; р₅ = 7 (все вращательные).

Звено 2 – базисное.

2. На рис. 1.16, б изображен более сложный механизм. Он имеет 7 подвижных звеньев и 10 кинематических пар, причем одна из них поступательная (Х).

Для определения класса механизма надо:

а) подсчитать степень свободы механизма по формуле Чебышева:

В данном механизме одно ведущее звено (в нашем примере – звено 5);

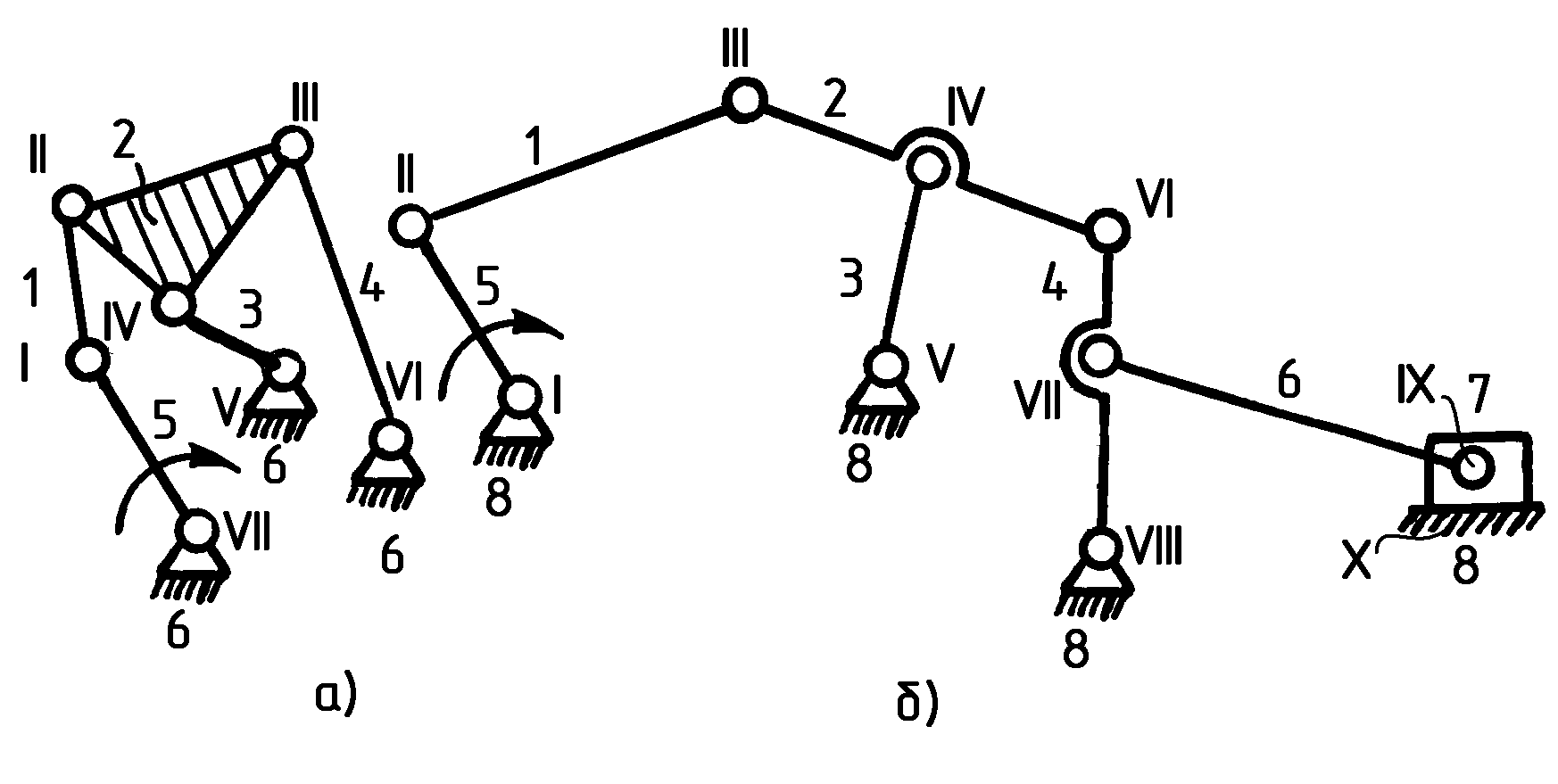
Рис. 1.16

б) отсоединяем самую отдаленную от ведущего звена группу Ассура II класса и проверяем подвижность оставшегося механизма. Самой удаленной является группа Ассура II класса, состоящая из звеньев 6 и 7 и кинематических пар VII, IX, X. Остался механизм из пяти подвижных звеньев и семи кинематических пар. Его подвижность не изменилась ( ), значит, отсоединение выполнено правильно;

в) отсоединяем следующую группу Ассура и тоже II класса, после чего проверяем подвижность, которая не должна меняться. Группа II класса состоит из звеньев 4 и 2, но после отсоединения механизм распадается, поэтому отсоединяем группу III класса, состоящую из четырех звеньев (1, 2, 3, 4) и шести кинематических пар (II, III, IV, V, VI и VIII). Проверив подвижность оставшегося ведущего звена ( ), делаем вывод, что данный механизм состоит из ведущего звена 5, групп Ассура III и II класса. Его формула строения будет:[5] → [1, 2, 3, 4] → [6, 7].

Класс механизма определяется наивысшим классом групп Ассура, входящих в состав механизма. Значит данный механизм III класса.

2. Классификация механизмов

В основе классификации механизмов лежат качественные и количественные характеристики строения механизма и его движения. Наиболее распространены следующие классификации.

П о г е о м е т р и ч е с к и м и к о н с т р у к т и в н ы м п р и з н а к а м:

1. Рычажные (рис. 1.1; 1.17), звенья 1, 2, 3, … образуют только вращательные, поступательные, цилиндрические или сферические кинематические пары А, В, С, …, Е.

2. Зубчатые (рис. 1.18), в которых зубчатые колеса 1, 2 образуют вращательные или поступательные пары.

3. Кулачковые (рис. 1.19), в состав которых входит кулачок с переменной кривизной профиля и толкатель, образующий высшую пару с поверхностью кулачка.

4. Фрикционные – передача движения осуществляется силами трения.

5. Механизм с остановками выходного звена. На рис. 1.20, а показан мальтийский механизм, на рис. 1.20, б – храповый.

Кроме перечисленных следует назвать еще механизмы с гибкими связями, пневматические, гидравлические, с электромагнитными и электронными элементами, комбинированные механизмы.

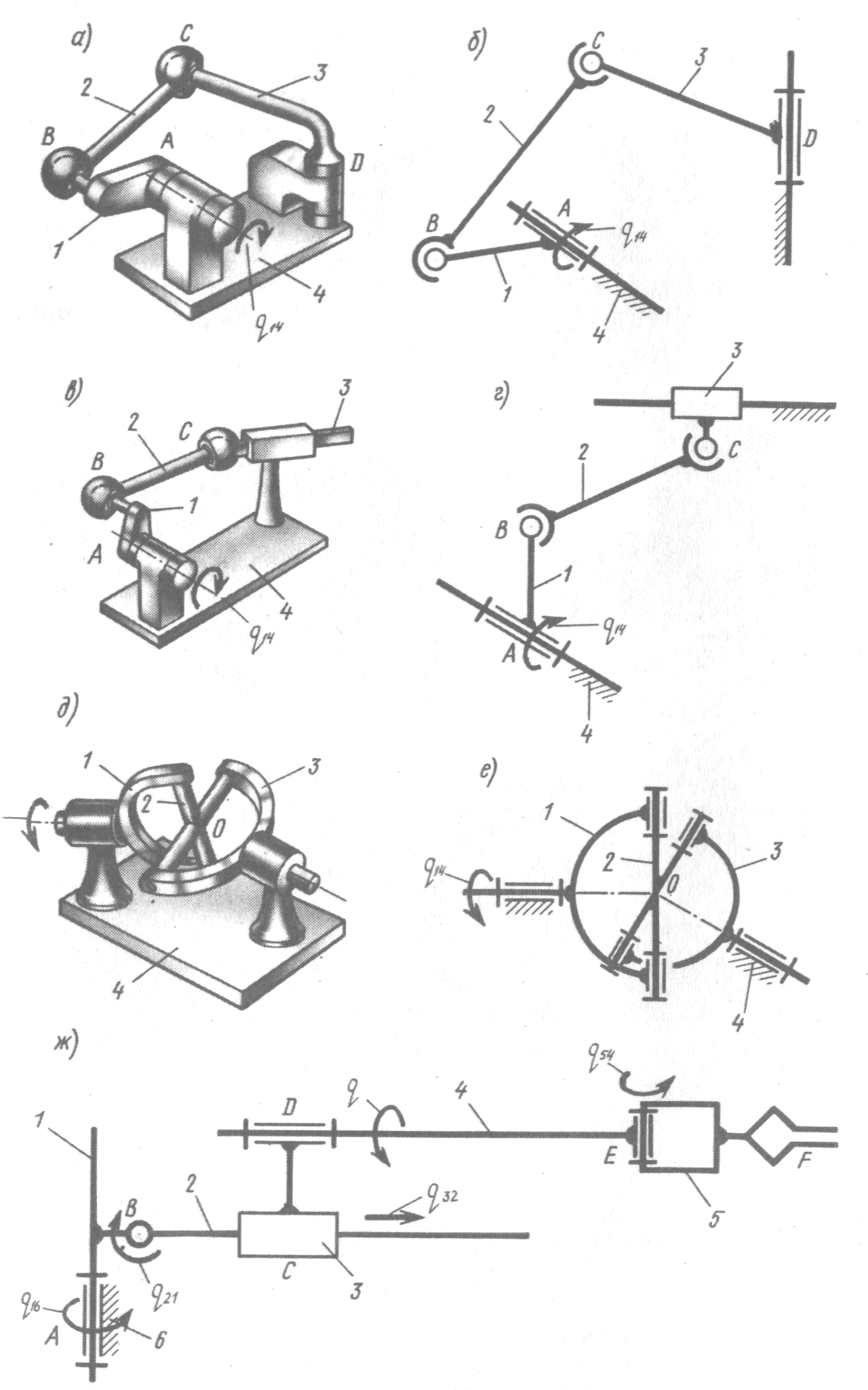
Рис. 1.17

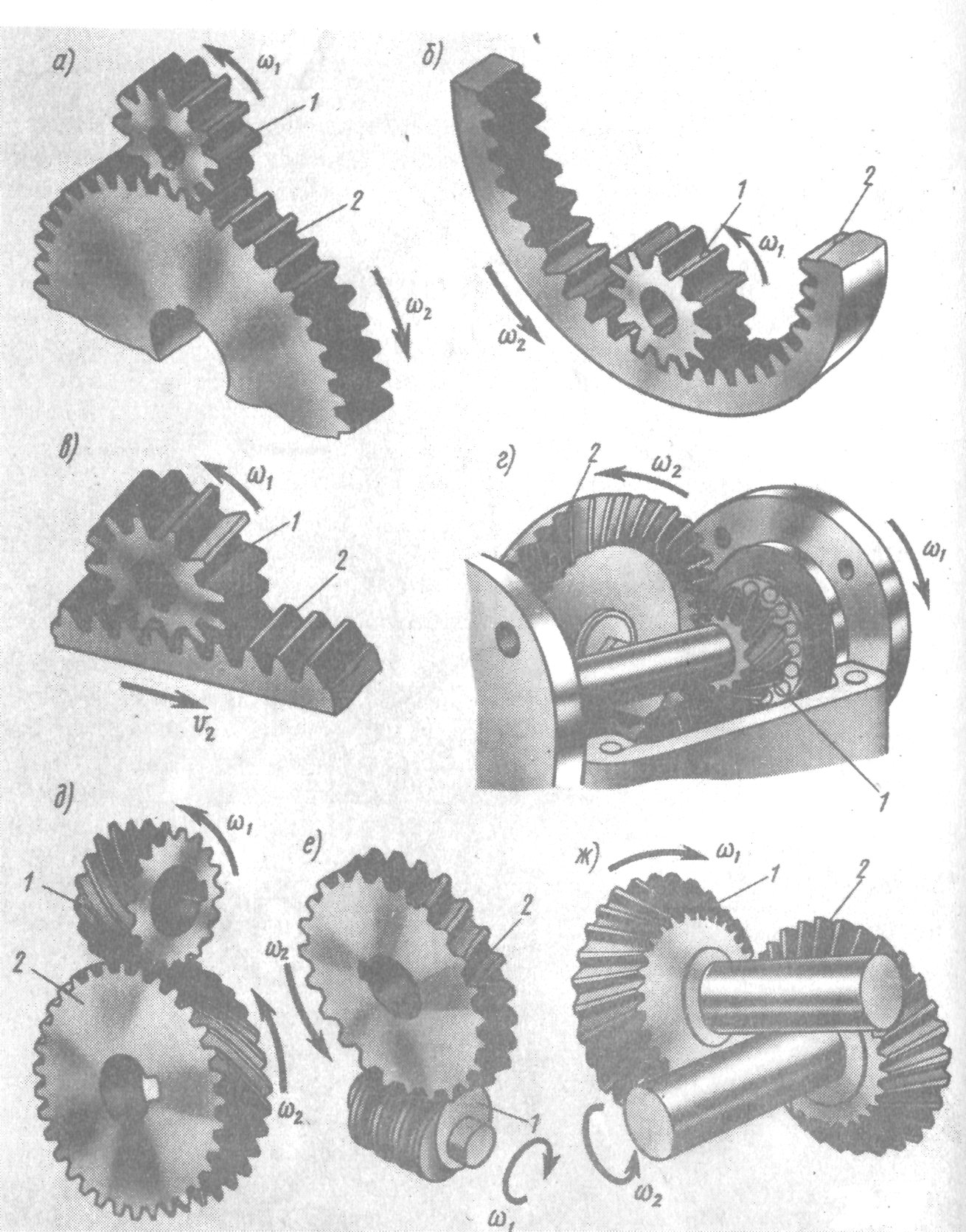
Рис. 1.18

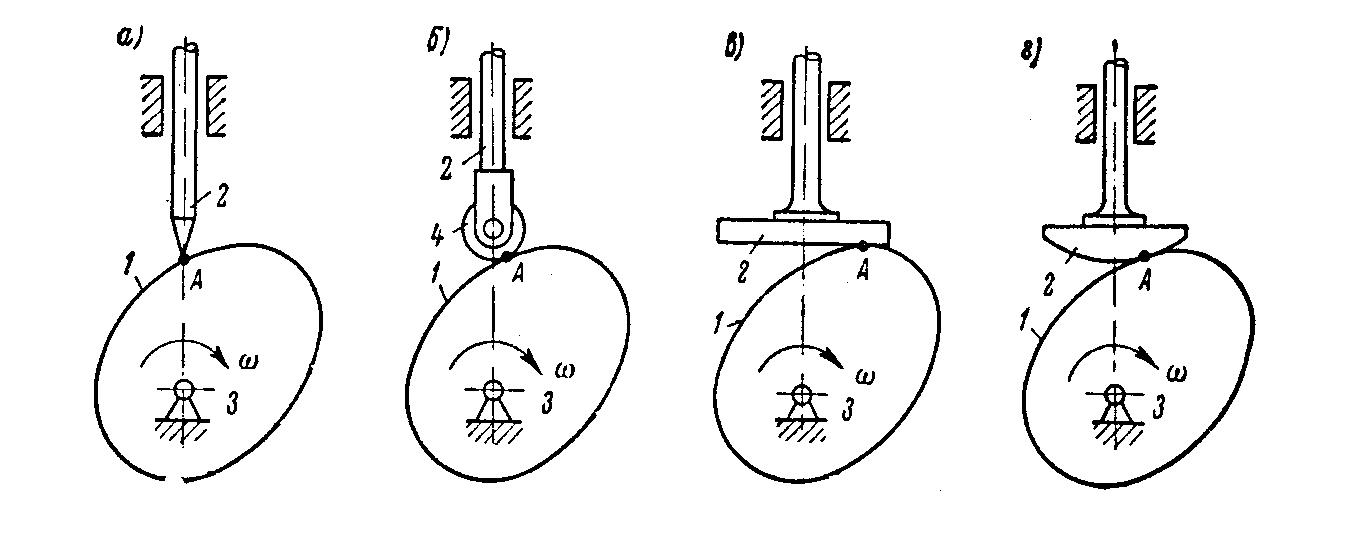
Рис. 1.19

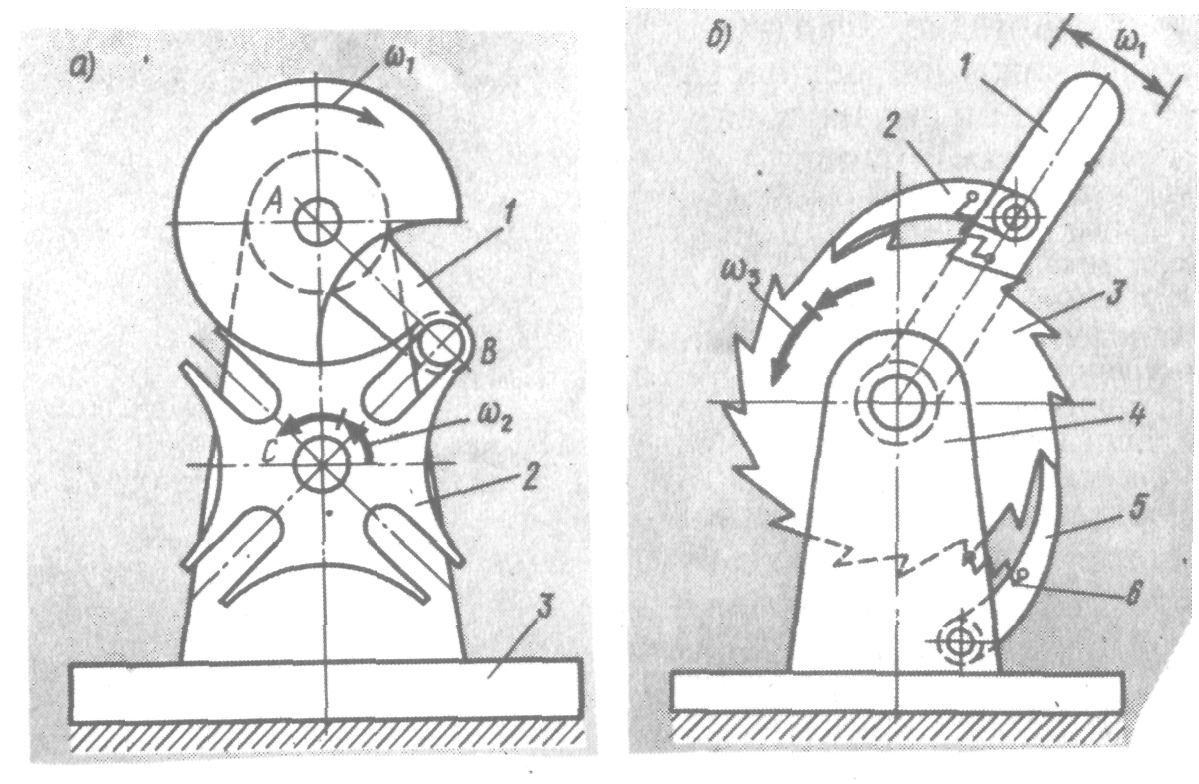
Рис. 1.20

П о ф у н к ц и о н а л ь н о м у н а з н а ч е н и ю и к и н е м а т и ч е с к о й п е р е д а т о ч н о й ф у н к ц и и с к о р о с т и и с п о л н и т е л ь н о г о з в е н а:

1. Механизмы с постоянным передаточным отношением (зубчатые, ременные, червячные, фрикционные и др.).

2. Механизмы со ступенчато изменяющимся передаточным отношением (коробки перемены скоростей, ступенчатые ременные и цепные передачи и др.).

3. Механизмы для сообщения возвратно-поступательного движения с постоянной скоростью

4. Механизмы для движения с остановками исполнительного органа (кулачковые, мальтийские, анкерные, храповые и др.).

5. Механизмы различного специального назначения (захватов, систем управления, реверсивные и др.).

П о с т р у к т у р е к и н е м а т и ч е с к о й ц е п и:

1. Замкнутые и незамкнутые.

2. По степени подвижности звеньев в замкнутом контуре, незамкнутой открытой и разветвленной цепи.

3. Специального назначения.

3. Способы преобразования механизмов

   на примере шарнирного четырехзвенного механизма

Одной из наиболее часто возникающих проблем, при создании шарнирных механизмов (особенно при преобразовании вращательного движения в возвратно-поступательное и наоборот), является требование проворачиваемости их звеньев, то есть наличия в них кривошипа или звена, способного иметь полное вращательное движение. При выполнении условия проворачиваемости возможно приведение механизмов в движение от электродвигателя.

1. Условия существования кривошипа

в плоских четырехзвенных механизмах

При синтезе механизмов весьма большое значение имеют соотношения между длинами звеньев.

Связь между размерами звеньев четырехзвенных механизмов и их движением может быть представлена математически в виде неравенств. Рассмотрим на примере механизма шарнирного четырехзвенника АВСD (рис. 1.21), длины звеньев которого обозначены через а, b, c, d. Требуется выяснить, при каких условиях звено АВ будет кривошипом, то есть будет проворачиваться на угол 2π, если принято, что а ‹ b ‹ c ‹ d.

Звено а станет кривошипом, если оно последовательно пройдет через крайнее левое (АВ₁) и правое (АВ₃) положения.

Считаем, что звено а самое короткое, d – самое длинное. Рассмотрев соответствующие треугольники и, используя известное соотношение между длинами сторон треугольника (длина стороны треугольника меньше суммы длин двух других его сторон), запишем неравенства:

из Δ В₁С₁D

d + a ‹ b + c, (1.9)

из Δ В₃С₃D

d - a ‹ b + c, (1.10)

Независимо от соотношения длин b и с неравенство (1.9) всегда обеспечит выполнение неравенства (1.10).

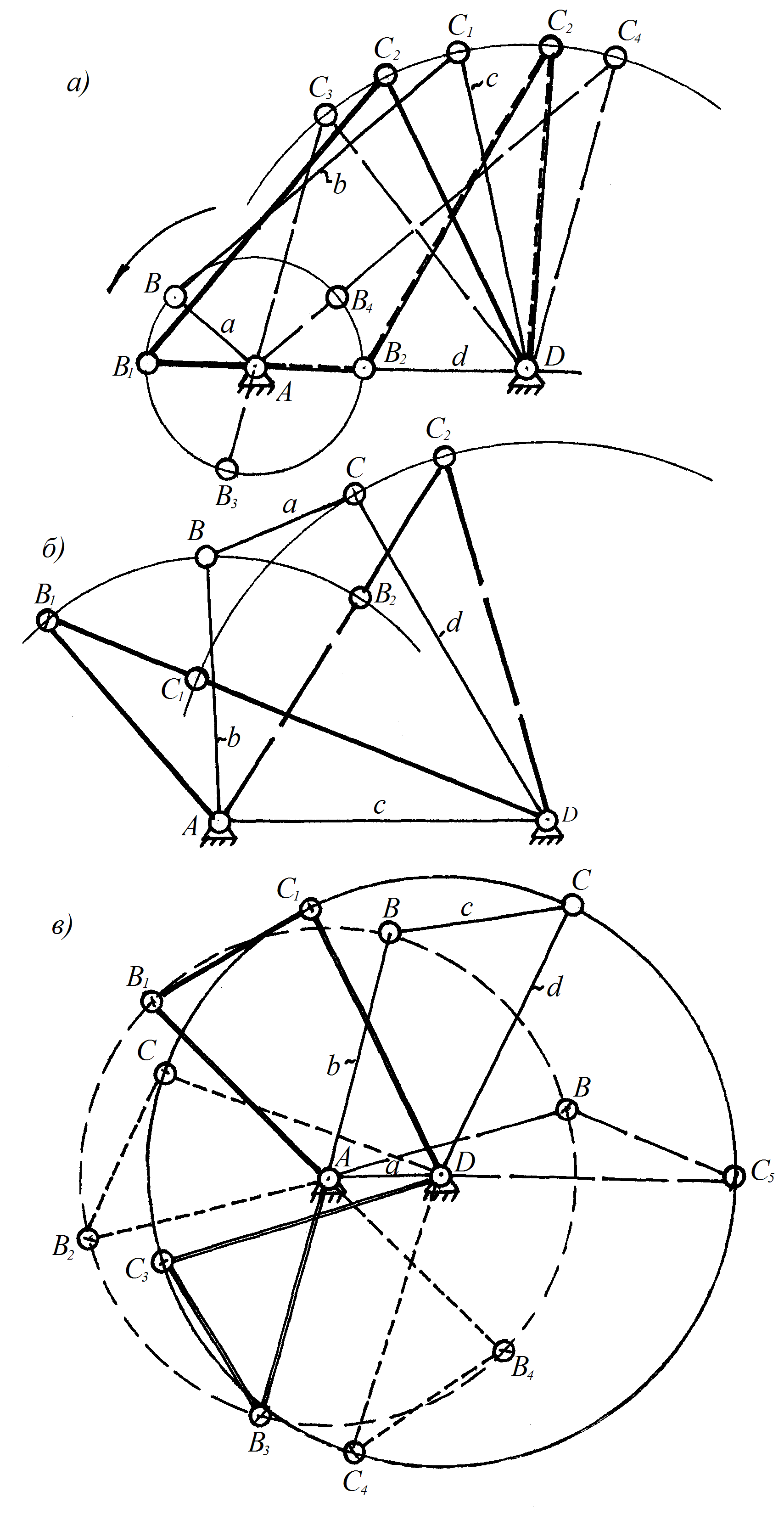
Рис. 1.21

Если самым длинным будет звено ВС или СD (b › с › d или с › b › d), то неравенство (1.10) только усиливается.

Позиции АВ₂ и АВ₄ характеризуют крайние положения звена СD (коромысла). Звено ВС не совершает полного оборота относительно стойки АD (см. рис. 1.21) и поэтому является шатуном.

Таким образом, самое короткое звено является кривошипом, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев. Это положение носит название правила Грасгофа.

Применяя это правило, шарнирные четырехзвенники разбивают на три группы:

1. к р и в о ш и п н о – к о р о м ы с л о в ы й (см. рис. 1.21, а), если размеры его звеньев удовлетворяют правилу, а за стойку принято звено, расположенное рядом с самым коротким звеном;

2. д в у х к о р о м ы с л о в ы й (см. рис. 1.21, б), если размеры его звеньев не удовлетворяют правилу или когда сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, но самое короткое звено является шатуном.

3. д в у х к р и в о ш и п н ы й (см. рис. 1.21, в), если его размеры удовлетворяют правилу Грасгофа и за стойку принято самое короткое звено; это следует из того, что если кривошип при выполнении правила делает полный оборот относительно стойки и шатуна, то и эти звенья совершают полный оборот относительно кривошипа.

16