Затухающие колебания
Затухающие колебания -
Линейная колебательная система -
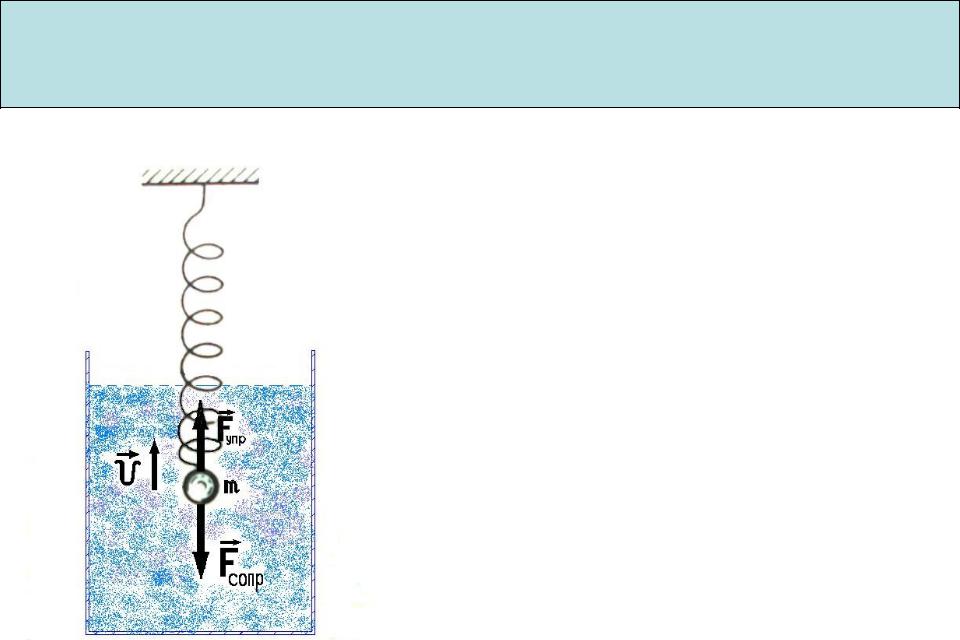
Дифференциальное уравнение затухающих колебаний
1. Пружинный маятник
Fсопр rν сила сопротивления среды (сила трения)
r коэффициент сопротивления среды
r кгс
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma Fi |
|
|
|
|
|
|
k |
|
|
|
r |
|
(3) |
|||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x m x m x 0 |
|||||||||||||||
ma Fупр Fсопр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
х 0 |
(4) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x 2 x 0 |
|||||||||||||||
Fсопр rν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
k |
|
0 |
|
цикл. частота |
|
|||||||||||||
max kx rνx |
|
|
|
|
|
|
|
|
||||||||||||||||
(1) |
|
|
|
|
|
m |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
гарм. колебаний |
|||||||||||||||
νx |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||||||
dt |
x |
|
|
|
|
|
|
коэффициент |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2m |
|
|
||||||||||||
|
dνx |
|
|
d 2 x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
затухания |
|
|
||||
ax |
|
|
|
|
dt2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с 1 |
|
||||||||
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
mx rx kx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальное уравнение
затухающих колебаний пружинного маятника:
x 2 x 02 x 0
Решение дифференциального уравнения затухающих колебаний пружинного маятника
x(t) A e t cos ( t |
) |
или |
x(t) A e t sin ( t |
) |
||
0 |
0 |
|
|
0 |
0 |
|
A(t) A0 e t амплитуда затухающих колебаний A0 начальная амплитуда (при t 0)
02 2 циклическая частота затухающих колебаний
0
T 2 период затухающих колебаний
T0 2 период гармонических
0 (незатухающих) колебаний
Так как 0 , то Т T0
|
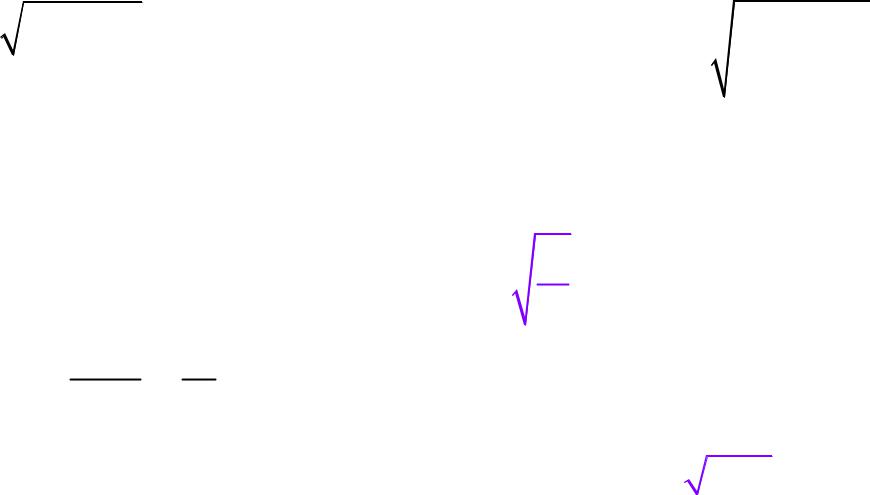
02 2 |
циклическая частота |
|
k |
|
r2 |
|
|
|
затухающих колебаний |
|
|
|||
|
|
m |
4m2 |
||||
|
Рассмотрим случай, когда |
0 |
|
|
|
|
|
Коэффициент затухания mk
r2 k 4m2 m
Коэффициент сопротивления среды r 4km
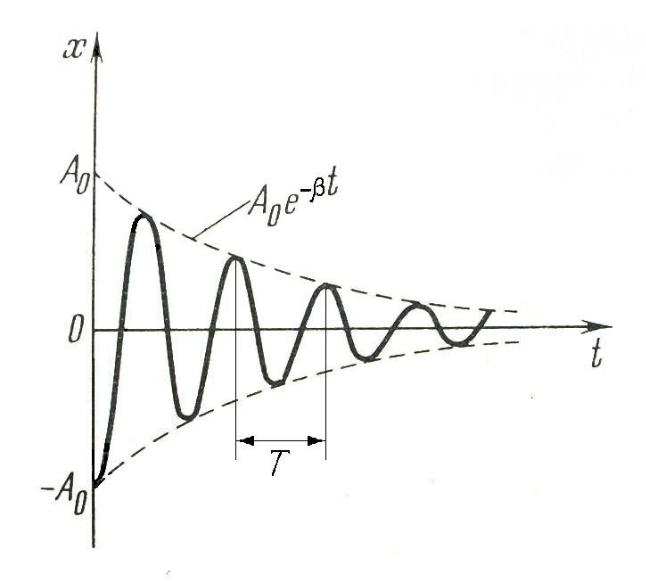
x(t) A0e t cos ( t 0 )
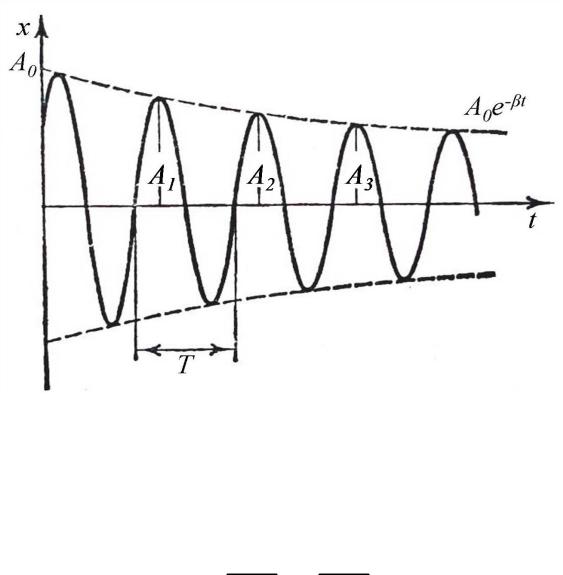
A1 A0e t
A2 A0e (t T ) A0e t e T A1 e T
A3 A0e (t 2T ) A0e (t T ) e T A2 e T
A1 A2 e T
A2 A3
ln |
A(t) |
ln e T T |
|
|
|||
A(t T ) |
|||
|
|
Логарифмический декремент затухания
ln |
A(t) |
T |
A(t T ) |
||
|
|
|
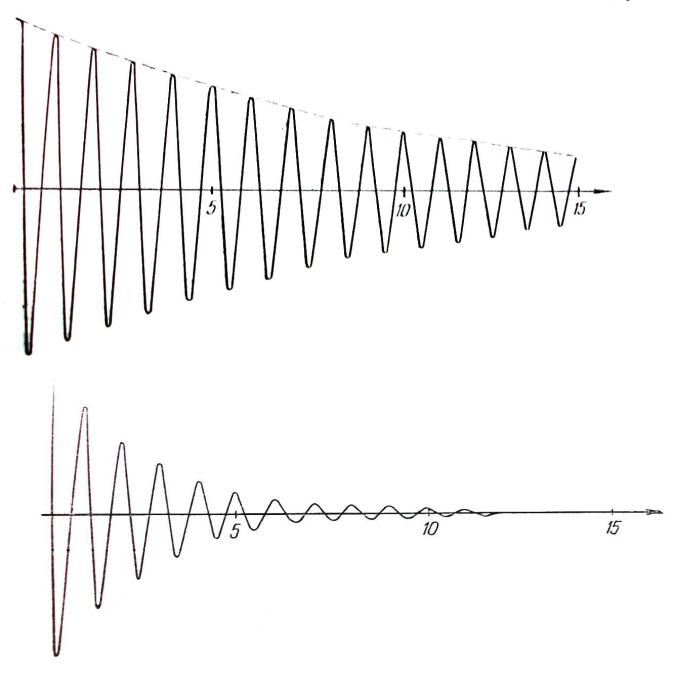
1 0,1c 1
T1 1c
1 1T1 0,1
2 0, 4 c 1
T2 1с
2 2T2 0, 4
1 2
|
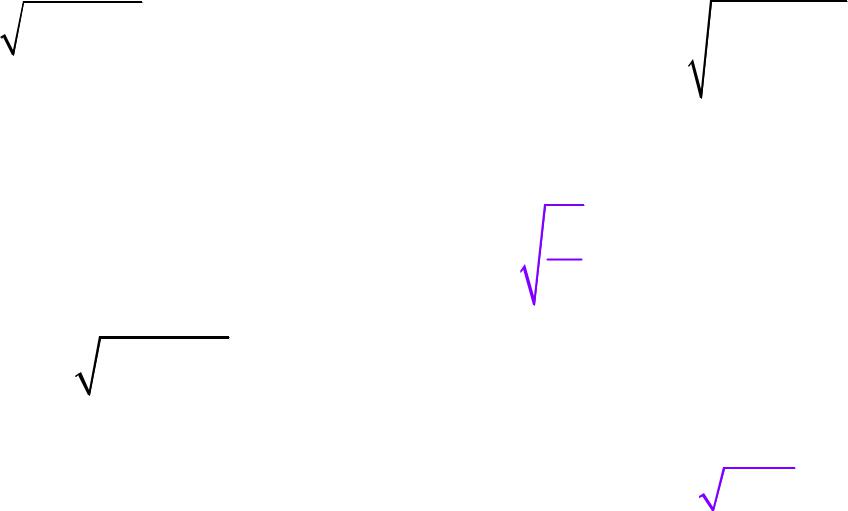
02 2 |
циклическая частота |
|
k |
|
r2 |
|
|
|
затухающих колебаний |
|
|
|||
|
|
m |
4m2 |
||||
Рассмотрим случай, когда |
0 |
|
|
|
|
||
Коэффициент затухания mk
i 2 02
Коэффициент сопротивления среды r 4km