
3-й семестр / Семинары / 12
.pdfРТУ МИРЭА Кафедра ВМ-2
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
3 СЕМЕСТР
Преподаватель: Горшунова Татьяна Алексеевна – доцент кафедры ВМ-2
e-mail: gorshunova@mirea.ru

РТУ МИРЭА Кафедра ВМ-2
Практическое занятие 12
Интегрирование функций комплексного переменного
Рассмотрим однозначную функцию ( ), определенную и непрерывную в области и кусочно-гладкую кривую , лежащую в .
Теорема. Если ( ) определена и непрерывна на , то существует ∫ ( ) .
Пусть = + , ( ) = + , где ( , ), ( , ) – действительные функции переменных и .
Вычисление интеграла от функции ( ) комплексного переменного сводится к вычислению обычных криволинейных интегралов от действительной и мнимой частей, а именно:
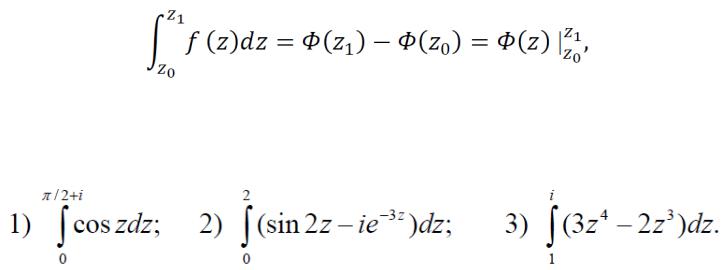
РТУ МИРЭА Кафедра ВМ-2
Теорема Коши для односвязной области. Если функция ( ) аналитична в односвязной области , то интеграл от этой функции вдоль любого замкнутого
контура , лежащего в , равен нулю: ( ) = 0.
Интеграл от аналитической функции, взятый по любой дуге в односвязной области, зависит только от начальной и конечной точек этой дуги, и потому одинаков для всех кривых, имеющих общую начальную 0 и конечную 1.
Если функция ( ) аналитична в односвязной области , содержащей точки 0 и 1, то имеет место формула Ньютона-Лейбница:
где ( ) – какая-либо первообразная для функции ( ), т.е. ′() = ( ) в области .
Пример. Вычислить интегралы от аналитических функций:
Решение.
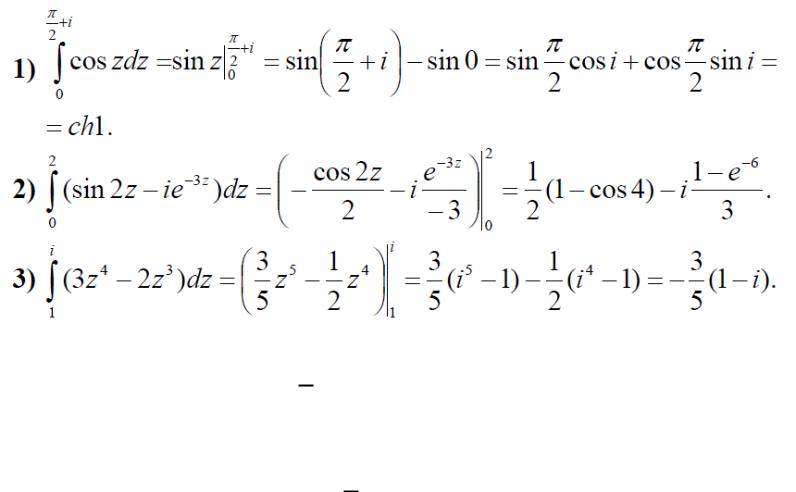
РТУ МИРЭА Кафедра ВМ-2
Задача 1. Вычислить интеграл ∫ ( + ) , – контур треугольника с вершинами в точках 1 = −1, 2 = −2 + , 3 = −1 + .
Задача 2. Вычислить интеграл ∫ ( + ) , – граница области | | < 2, > 0.

РТУ МИРЭА Кафедра ВМ-2
Задачи для самостоятельного решения
1.Вычислить определённый интеграл
2.Вычислить интеграл ∫ (2 + ) по дуге : = 2 от точки 1 = 0 до
2 = 4 − 2 .
3.Вычислить интеграл ∫ 2 по отрезку от точки 1 = 0 до 2 = 2 + 2.
РТУ МИРЭА Кафедра ВМ-2
Ряды с комплексными членами. Ряды Тейлора и Лорана
Теорема. Функция ( ), аналитичная в круге | − 0| < , разлагается в нем
единственным образом в сходящийся к ней степенной ряд Тейлора
∞
( ) = ∑ ( − 0) ,
=0
коэффициенты которого вычисляются по формулам
|
1 |
|
( ) |
|
( )( |
) |
||
= |
|
∫ |
|
|
= |
0 |
|
, ( = 0,1, . . . ), |
|
|
|
|
|
||||
|
2 |
(− |
) +1 |
|
! |
|
|
|
|
|
|
0 |
|
|
|
|
|
где – окружность с центром 0, целиком лежащая в круге сходимости ряда
| − 0| < .
Предполагается, что окружность проходится в положительном направлении, т.е. против часовой стрелки.
Справедливы следующие разложения в ряд Тейлора в окрестности точки 0 = 0.
= 1 + + |
2 |
+. . . + |
|
+. . . = ∑∞ |
|
, = ∞ |
|
||||||||
|
|
|
|
||||||||||||
|
|
|
2! |
|
! |
=0 |
! |
сх |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
sin = − |
3 |
|
+ + (−1) |
2 +1 |
|
|
+ = ∑∞ |
(−1) |
2 +1 |
, = ∞ |
|||||
|
|
|
|
|
|||||||||||
3! |
|
|
|
|
|
(2 +1)! |
|
|
=0 |
|
(2 +1)! |
сх |
|||
|
|
|
|
|
|
|
|
|
|
||||||

РТУ МИРЭА Кафедра ВМ-2
= 1 − |
2 |
+. . . +(−1) |
|
|
2 |
+. . . = ∑∞ |
(−1) |
|
2 |
|
|
, = ∞ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2! |
|
|
|
|
|
(2 )! |
|
|
|
|
=0 |
|
(2 )! |
сх |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
−1 |
|
|
|
|
∞ |
|
|
−1 |
|
|
|||||||
(1 + ) = − |
|
+ |
|
− + (−1) |
|
|
|
|
|
+ = |
∑ (−1) |
|
|
, = 1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
сх |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
( −1) |
2 |
|
|
|
|
( −1)...( − +1) |
|
|
|
|
|
|
|
|
|||||||||||
(1 + ) = 1 + + |
|
|
|
|
|
+. . . + |
|
|
|
|
|
|
|
|
|
|
+. .. , |
= 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
сх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при = −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
= 1 − + 2−. . . +(−1) +. . . = ∑∞ |
(−1) , = 1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
сх |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= 1 + + 2+. . . + +. . . = ∑∞ |
|
|
, = 1. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1− |
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
сх |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача. Разложить в ряд Тейлора по степеням :
1)( ) = +2
2)( ) = ln (3 + )
3)( ) = 2 3−5
РТУ МИРЭА Кафедра ВМ-2
Ряд Лорана
Определение. Рядом Лорана называется ряд вида:
… + |
− |
+ + |
−1 |
+ |
+ ( − ) + |
( − )2 |
+ + |
( − ) + = |
||||||
( − ) |
− |
|||||||||||||
|
|
|
0 |
1 |
0 2 |
0 |
|
|
|
0 |
||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
∞ |
|
− |
|
|
|
|
|
|
|
|
|
|
= ∑ |
( − ) + ∑ |
|
|
, |
|
|||
|
|
|
|
|
|
( − |
) |
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
=0 |
|
=1 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
где , |
– комплексные постоянные, а – комплексная переменная. |
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Функция ( ), однозначная и аналитическая в кольце < | − 0| < (не исключаются случаи = 0 и = +∞), разлагается в этом кольце единственным образом в сходящийся к ней ряд Лорана
∞ −1 ∞
|
|
( ) = ∑ |
( − ) = ∑ |
( − ) + ∑ |
( − ) |
|
|||
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
=−∞ |
|
=−∞ |
|
=0 |
|
|
Ряд |
∑∞ |
|
( − ) называется правильной частью ряда Лорана, а ряд ∑∞ |
− |
|||||
|
|||||||||
|
=0 |
|
0 |
|
|
|
|
=1 ( − ) |
|
|
|
|
|
|
|
|
|
|
0 |
называется главной частью ряда Лорана.

РТУ МИРЭА Кафедра ВМ-2
На практике при нахождении коэффициентов используют готовые разложения в ряд Тейлора элементарных функций.
Пример. Разложить в ряд Лорана функцию ( ) = 2 1 в окрестности точки
0 = 0.
Решение. Для любого комплексного имеем:
cos = 1 − |
2 |
+. . . +(−1) |
|
2 |
+. . . = ∑∞ |
(−1) |
2 |
, |
= ∞ |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2! |
|
|
|
|
|
|
|
|
|
(2 )! |
|
|
|
|
|
|
|
|
=0 |
|
|
(2 )! |
сх |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставляя = |
1 |
, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
||||||||||
2 cos |
|
|
= 2 (1 − |
|
|
|
+ |
|
|
|
− |
|
|
+. . . +(−1) |
|
|
|
|
+ ) = |
|||||||||||||||||||
|
2! 2 |
|
4! 4 |
6! 6 |
(2 )! 2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
= 2 − |
|
|
|
+ |
|
|
|
− |
|
|
+ (−1) |
|
|
|
+ = |
|
|||||||||||||||||
|
|
|
|
|
2! |
4! 2 |
6! 4 |
(2 )! 2 −2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 |
+ 2 + |
|
|
1 |
|
|
1 |
|
|
+ (−1) |
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
= − |
|
|
|
− |
|
|
|
+ . |
|
|||||||||||||||||||||||
|
|
|
|
|
|
2! |
4! 2 |
6! 4 |
(2 )! 2 −2 |
|
||||||||||||||||||||||||||||
Это разложение справедливо для любой точки ≠ 0, т.е. в кольце 0 < | | < +∞.

РТУ МИРЭА Кафедра ВМ-2
= 0, = +∞. В этом кольце функция является аналитической.
−2!1 + 2 является правильной частью ряда Лорана,
1 |
|
1 |
+ (−1) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
− |
|
|
|
+ является главной частью ряда Лорана. |
|
|
|
|||||||||||||||||||||
|
4! 2 |
6! 4 |
(2 )! 2 −2 |
|
|
|
|||||||||||||||||||||||||
Пример 2. Разложить функцию ( ) = |
|
1 |
|
|
в ряд Лорана в области | | > |
2 |
по |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2+3 |
|
3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
степеням . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Преобразуем функцию |
( ) = |
|
|
= |
|
|
|
∙ |
|
|
|
|
|
и используем разложение: |
|
|
|
||||||||||||||
2+3 |
3 |
1+ |
2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
= 1 − + 2 − 3 + + |
(−1) + , |
сходится при | | < 1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 + |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
( ) = |
|
1 |
|
= |
1 |
|
∙ |
1 |
|
= |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 + 3 |
|
3 |
1 + |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
