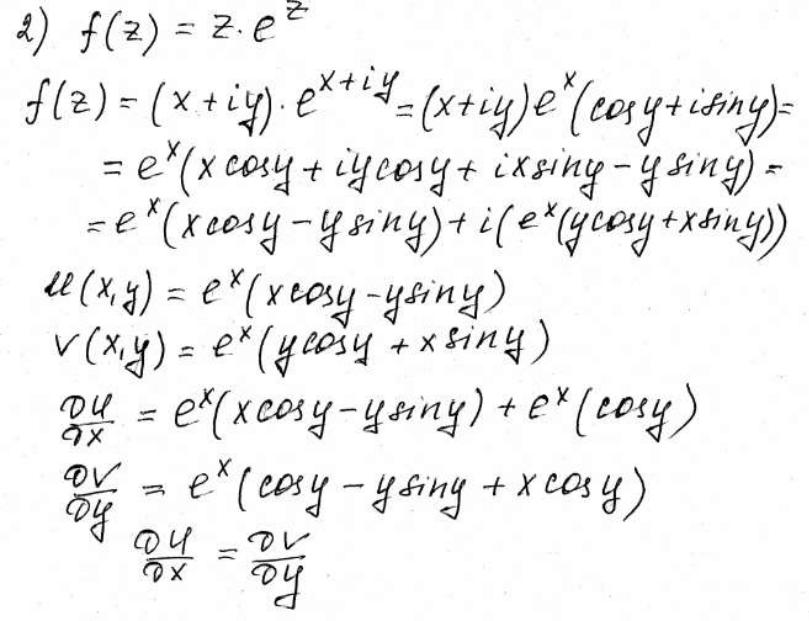3-й семестр / Лекции / 11 - презентация

5. Если кривая задана параметрическими уравнениями

= ( ) { = ( ),

начальная и конечная точки дуги соответствуют значениям параметра = 0, = 1, то

1

∫ ( ) = ∫ [ ( )] ′( ),

0

где ( ) = ( ) + ( ).

Примеры.

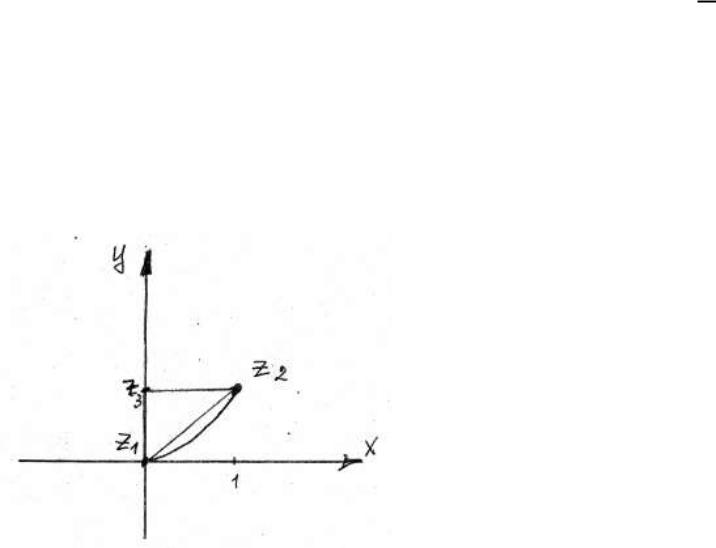
Пример 1. Вычислить интеграл ∫ (1 + − 2) по линиям, соединяющим точки 1 = 0, 2 = 1 + .

а) по прямой б) параболе = 2

в) по ломаной 1 3 2, 3 = 1.

Перепишем подынтегральную функцию в виде

1 + − 2 = 1 + − 2( − ) = (1 − 2 ) + (2 + 1), т.е. ( , ) = 1 − 2 , ( , ) = 2 + 1.

Проверим условия Коши-Римана

= −2, = 2

– первое условие не выполняется, т.е. подынтегральная функция не аналитична.

∫(1 + − 2 ) =

= ∫(1 − 2 ) − (1 + 2 ) + ∫(1 − 2 ) + (1 + 2 ) .

a)Уравнение прямой, соединяющей точки 1 = 0, 2 = 1 + :

= , 0 ≤ ≤ 1, =

∫ (1 − 2 ) − (1 + 2 ) + ∫ (1 − 2 ) + (1 + 2 ) =

=∫01(1 − 2 − 1 − 2 ) + ∫01 2 = −2 2 + 2 |10 =

=−2 + 2 .

б) Для параболы = 2; = 2 ; 0 ≤ ≤ 1.

∫ (1 − 2 ) − (1 + 2 ) + ∫ (1 − 2 ) + (1 + 2 ) = = ∫01(1 − 2 − (1 + 2 2)2 ) + + ∫01(1 + 2 2 + (1 − 2 )2 ) =

в) 1 3: = 0; = 0; 0 ≤ ≤ 1.

3 2: = 1; = 0; 0 ≤ ≤ 1.

∫ (1 − 2 ) − (1 + 2 ) + ∫ (1 − 2 ) + (1 + 2 ) =

∫ 1 3 + ∫ 3 2 =

1 1 1 1

= ∫0 (1 − 2 ) + ∫0 − ∫0 (1 + 2 ) + ∫0 (1 − 2) = = ( − 2 + − − 2 − )|10 = −2 .

Интеграл зависит от пути интегрирования, так как функция не является аналитической.

Пример 2. Вычислить интеграл ∫0 cos . Функция ( ) =

аналитична всюду в комплексной плоскости. По свойству 4

∫0 cos = sin |0 = sin = 1.

Пример 3. Вычислить интеграл ∫2(3 2 + 1) .

Так как подынтегральная функция аналитична всюду (для проверки достаточно проверить все условия Коши-Римана), то можно применить формулу Ньютона-Лейбница

2

∫ (3 2 + 1) = ( 3 + ) |2 = (2 )3 + 2 − 3 − =

= −8 + 2 + − = −6 .

Дополнительные примеры и задания

1. Проверить функцию на аналитичность.

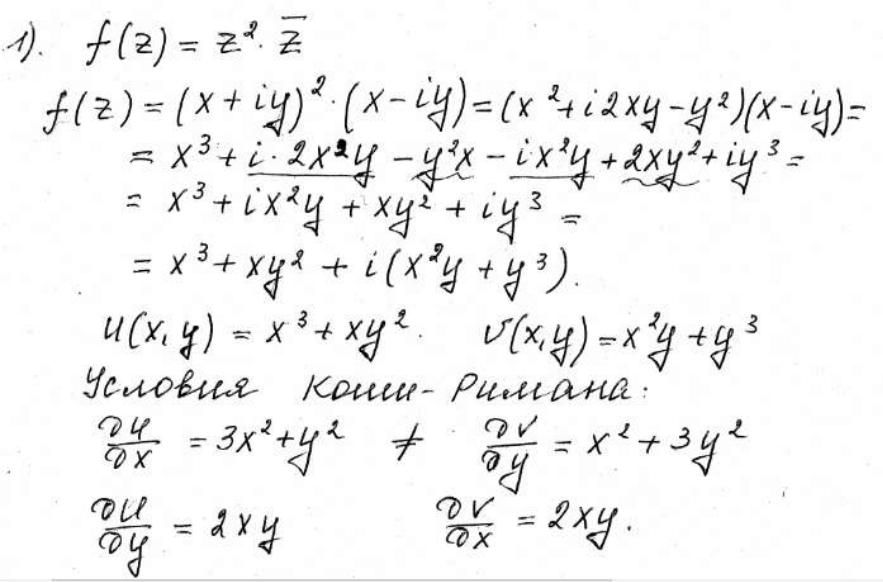
Условия Коши-Римана выполнены только в точке (0;0).

В этой точке функция дифференцируема, аналитической не является ни в одной точке комплексной плоскости.