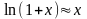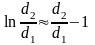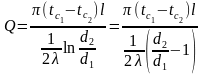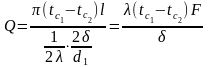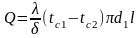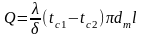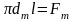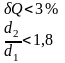- •Віды цеплаабмену.
- •Магутнасць і шчыльнасць цеплавой плыні.
- •Асноўны закон цеплаправоднасці (закон Фур’е). Каэфіцыент цеплаправоднасці.
- •Цеплаперадача. Раўнанне цеплаперадачы праз плоскую аднаслойную і шматслойную сценку. Каэфіцыент цеплаперадачы.
- •Канвектыўны цеплаабмен. Цеплааддача. Раўнанне цеплааддачы (Ньютана-Рыхмана).
- •Каэф'щыент цеплааддачы і фактры, якія наягоуплываюць.
- •Раўнанні падобнасці (крытэрыяльныя раўнанні) канвектыўнага цеплаабмену. Вызначальпы памер і вызначальная тэмпература.
- •Асаблівасціруху і цеплаабмену ў трубах.
- •Віды кандэнсацыі пары і асаблівасці цеплаабмену. Раўнанне цеплааддачы пры кандэнсацыі пары.
- •Уплыў розных фактарау на цеплааддачу пры кандэнсацыі пары.
- •Рэжымы кіпення ў вялікім аб’ёме і асаблівасці цеплаабмену. Раўнанне цеплааддачы пры кіпенні вадкасці.
- •Залежнасць цеплавой плыні і каэфіцыента цеплааддачы ад тэмпературнага напору (крывая кіпення). Крызісы кіпення.
- •Уплыўрозных фактараў на цеплааддачу пры кіпенні.
- •Закон цеплавога выпраменьвання Стэфана-Больцмана.
- •Цеплаабмен еыпраменъеаннем паміж паралельнымі паверхнямі.
- •Сонечная радыяцыя. Разлік цеплапрытокаў ад сонечнайрадыяцыі.
- •Асноўныя раўнанні цеплавога разліку цеплаабменных апаратаў: Раўнанне цеплавога балансу і яго варыянты. Раўнанне цеплаперадачы.
- •Сярэдні тэмпературны напор у цеплаабменным апараце.
- •Перадача ццеплыні нраз рабрыстую сценку.
- •Прывядзенне раўнанняў нестацыянарнай цеплаправоднасці да беспамер- нага выгляду. Лік Біа і лік Фур’е. Развязак для тэмпературнага поля і колькасці цеплыніў беспазмерным еыглядзе.
- •Віды масаабмену.
- •Малекулярная дыфузія. Канцэнтрацыйная дыфузія. Першы закон Фіка. Каэфіцыент дыфузіі.
- •Канвектыўны масаабмен (канеектыўная дыфузія). Масааддача. Каэфіцыент масааддачы.
Віды цеплаабмену.
а) Цеплапроводнасць-абмен цеплавой энергией увынику узаемадзеяння памиж атамами и молекулами. б)Канвекция – цеплаабмен перамяшчэннем макраскапичаских элементау серады у розных температурах.Канвекцыи у чыстым видзе не бывае.Канвекцыя саправаждаецца цеплаправоднасцью.Канвектыуны цеплаабмен-сумесны абмен канвекцыей и цеплаправоднасцю. В)Цеплаабмен выпраменьваннем(излучением)-
перанос цеплыни(энергии) электромагнитными хвалями.Пераносицца эл.магн-я энергия.Другое цела паглынае эл.магн-е хвали и другое цела ператварае эл-магн. энергию у цеплавую энергию.У цвердым целе узникае калебательны рух.
Магутнасць і шчыльнасць цеплавой плыні.
Цеплыня(q)
перадаецца у другом направвлении от
gradt.
q
или Q,
Вт ,
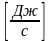 -магутнасць(мощность)
цеплавой плыни-колькасць
цеплыни праз паверху за адзинку часу.
У агульным выпадку шчыльнасць:
-магутнасць(мощность)
цеплавой плыни-колькасць
цеплыни праз паверху за адзинку часу.
У агульным выпадку шчыльнасць: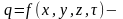 нестацыян.
цеплавая плынь
;
нестацыян.
цеплавая плынь
;
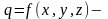 стацыян.
цеплавая плынь.
стацыян.
цеплавая плынь.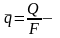 сярэдняя
шчыльнасць цеплавой плыни.
сярэдняя
шчыльнасць цеплавой плыни.
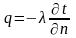 -цеплаправоднасць
прапарцыянальна градыенту темп-ры.
-цеплаправоднасць
прапарцыянальна градыенту темп-ры.
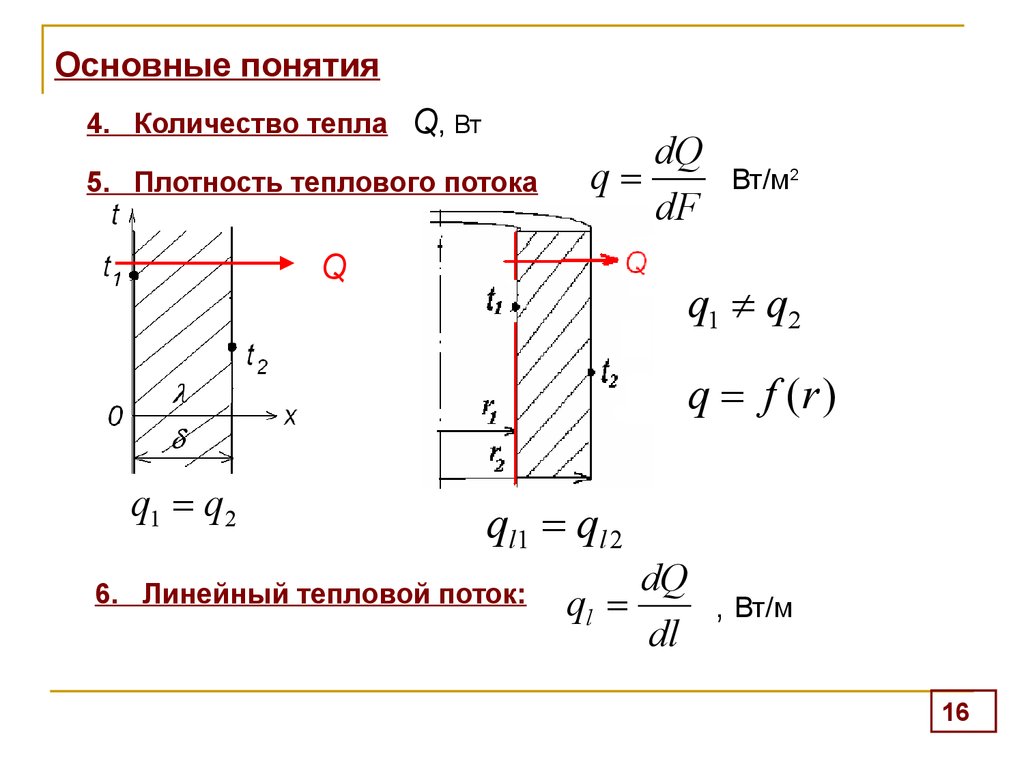
Асноўны закон цеплаправоднасці (закон Фур’е). Каэфіцыент цеплаправоднасці.
Пр-с
цеплаправоднасци
– узаемадзеяння микрачасцинак атамау
и малекулах у гащах и жыдкасцях, яны
сутыкаюцца друг з другам.У цвердых
целах
атамы и малекулы не сутыкаюцца,яны
тольки прыцягваюцца або атталкиваюцца.Гэта
вагальны(колебательны)
рух.У
металах прысутничае электроны
газ.Электроны легкия и шустра пераносяць
кинетычную энергию.Закон
Фур’е
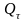 [Дж,кДж]
;
[Дж,кДж]
;
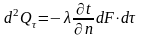
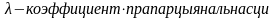
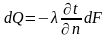 ,
,
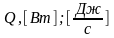 ,
,
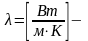 коэф-т
теплопроводности(характеризует
уласцивасць цела)
коэф-т
теплопроводности(характеризует
уласцивасць цела)
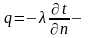 шчыльнасць(плотность)
цеплавой плыни - цеплаправоднасць
прапарцыянальна градыенту темп-ры.
шчыльнасць(плотность)
цеплавой плыни - цеплаправоднасць
прапарцыянальна градыенту темп-ры.
Раўнанне цеплаправоднасці праз плоскую аднаслойную і шматслойную сценку пры стацыянарным рэжыме і межавых умовах першага роду.
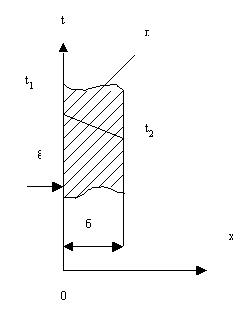 Рис.
3. Однослойная плоская стенка. Г.У. I рода.
Рис.
3. Однослойная плоская стенка. Г.У. I рода.
Дана однородная и изотропная стенка (рис.3) толщиной δ с постоянным коэффициентом теплопроводности λ, два других размера стенки неограниченны. На наружных поверхностях стенки поддерживают постоянные температуры t1 и t2. При заданных условиях температура будет изменяться только в направлении оси Ox, т.е. температурное поле будет одномерным и
∂t/∂y = ∂t/∂z = 0
Тогда уравнение принимает вид:
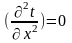 (25)
(25)
В уравнении (25) частная производная заменена полной, т.к. изменение температуры определяется только одной переменной X. Граничные условия в рассматриваемой задаче запишутся следующим образом:
При

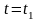 при
при
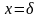
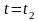 (26)
(26)
Уравнение (25) и условия (26) дают полную математическую формулировку рассматриваемой задачи.
В результате поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = ƒ(x), и получена формула для определения плотности теплового потока.
Проинтегрируем дважды уравнение (25).
Первое интегрирование дает:
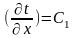 (27)
(27)
После второго интегрирования получим:
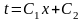 (28)
(28)
Постоянные
интегрирования: при
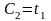 при
при
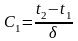
Закон распределения температуры в рассматриваемой плоской стенке или, иначе, выражение для температурного поля:
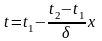 (29)
(29)
Для определения плотности теплового потока воспользуемся законом Фурье
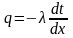 Учитывая,
что
Учитывая,
что
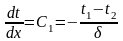
после подстановки dt/dx в выражение закона Фурье, получаем:
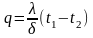 (30)
(30)
t1 - t2 = Δt - температурный напор;
отношение λ/δ, Вт/м2К- тепловая проводимость стенки;
обратная величина Rc = δ/λ, м2К/ Вт - термическое сопротивление теплопроводности стенки.
Найдя плотность теплового потока, можно вычислить все тепло, которое передается через поверхность стенки F за время τ:
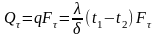 (31)
(31)
Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев (рис.4). Заданы толщины слоев δ1, δ2, δ3, . . . , δn , температуры на внешних поверхностях стенки t1 и tn+1 (в случае 3-слойной стенки t1 и t4), коэффициенты теплопроводности λ1, λ2, λ3, . . . , λn . Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова. Эти температуры t2 , . . ., tn неизвестны.
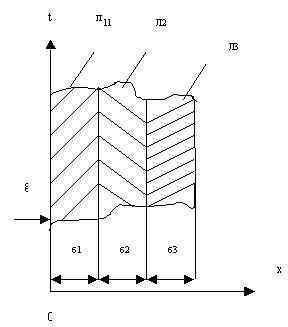 Рис.4.
Многослойная плоская стенка. Г.У. 1 рода.
Рис.4.
Многослойная плоская стенка. Г.У. 1 рода.
Т.к. мы рассматриваем стационарный процесс, то плотность теплового потока для всех слоев будет одинакова, и в соответствии с (30) можно записать:
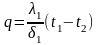
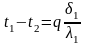
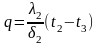 (а)
(а)
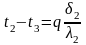 (б)
(б)
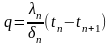
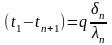
Сложив, левые и правые части уравнений (б), получим:
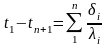
Отсюда
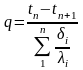 (33)
(33)
где Σδi/λi - термическое сопротивление теплопроводности многослойной стенки.
В общем случае i– номер слоя
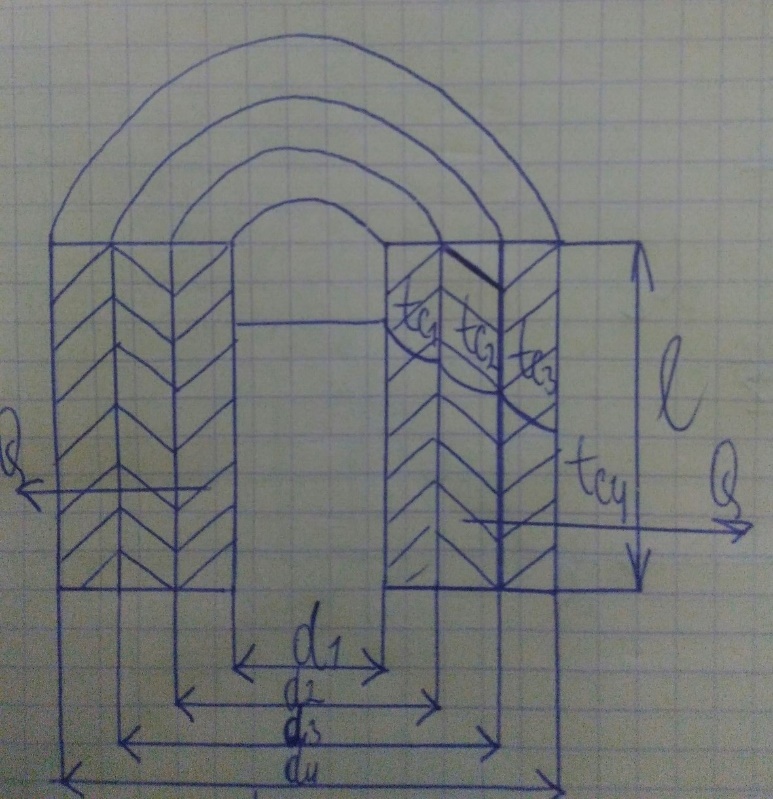
Раўнанне цеплаправоднасці праз цыліндрычпую аднаслойную і шматслойную сценку пры межавых умовах першага роду. Спрашчэнне разлікаў.
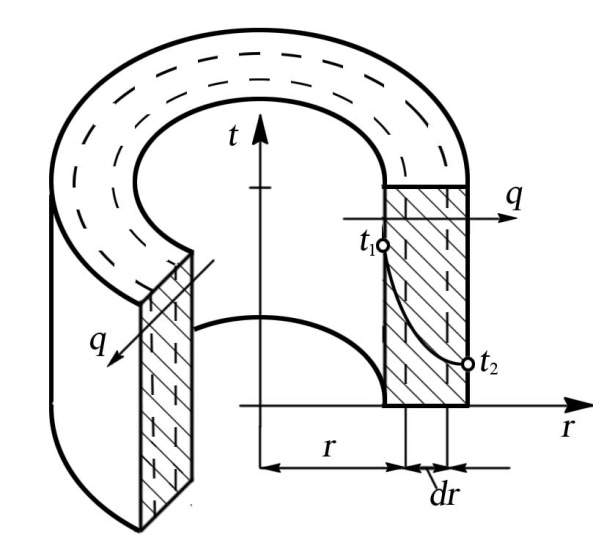
G6Рис. 9.6. Цилиндрическая однослойная стенка. Предполагаем, что температура не меняется по оси трубы и по окружности трубы, по углу φ (рис. 9.6.), т. е. как и в случае плоской стенки, задача является одномерной.
Теплота передается от внутренней поверхности к внешней.
Допустим, что стенка выполнена из однородного материала, коэффициент теплопроводности λ которого известен и не зависит от температуры. Известны также внутренний и наружный радиусы трубы r1, r2 и температуры внутренней и наружной поверхности t1и t2, которые не меняются во времени.
Выделим в стенке трубы цилиндрическую поверхность радиусом r, площадь которой:
![]()
где l – длина трубы.
Количество теплоты, переданной через эту поверхность, можно определить по уравнению Фурье:
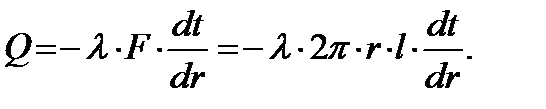
Выражение для температурного градиента здесь записано в виде dt/dr, поскольку температура стенки изменяется только в направлении радиуса.
Обозначая
![]() (2.16)
(2.16)
Перепишем исходное уравнение в виде dt=A(dr/r). После интегрирования получим
t=A ln r+B
Это
выражение показывает, что изменение
температуры в стенке цилиндрической
трубы подчиняется закону логарифмической
кривой (при
![]() =const
и при отсутствии внутренних источников
теплоты). Освободимся от постоянной
интегрирования B,
для чего воспользуемся граничным
условиями:
=const
и при отсутствии внутренних источников
теплоты). Освободимся от постоянной
интегрирования B,
для чего воспользуемся граничным
условиями:
tc1=A
ln r1+B
; tc2=A
ln r2+B
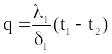
Вычтем из первого уравнения второе, тогда получим
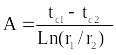 (2.18)
(2.18)
Тепловой поток можно определить, если найденное значение А из (2.18) подставить в (2.16) . При этом, чтобы устранить минус в левой части уравнения, надо под знаком логарифма изменить отношение радиусов на обратное. Тогда
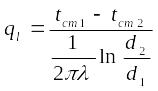 (в
числителе нужно дописать: умножить на
L)
(в
числителе нужно дописать: умножить на
L)
(и вместо q поставить Q)
Величина
![]() имеет
единицу измерения (м*К/Вт) и называется
линейным термическим сопротивлением
цилиндрической стенки.
имеет
единицу измерения (м*К/Вт) и называется
линейным термическим сопротивлением
цилиндрической стенки.
Плотность теплового потока
Поскольку внутренняя и внешняя поверхности трубы имеют различную площадь, значения плотности теплового потока qr1и qr2различны. Чтобы найти значение температуры на любом радиусе r в толщине цилиндрической стенки, проинтегрируем левую часть уравнения (9.26) в пределах от t1 до текущего значения температуры t,а правую – от r1до текущего значения радиуса r:
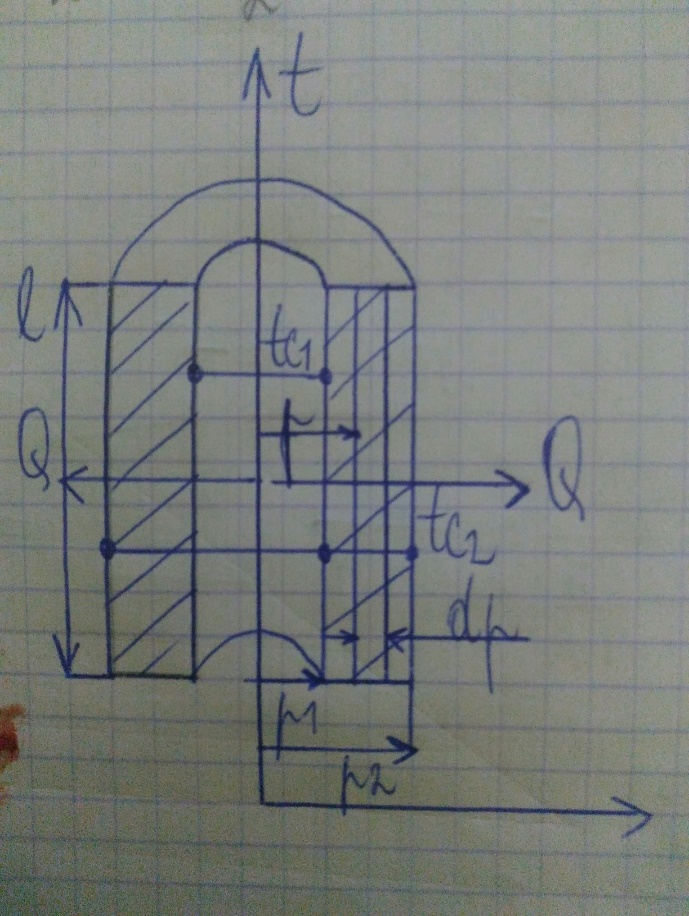
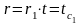
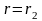
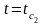
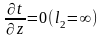
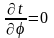
Стацыянарны
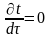
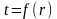
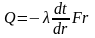
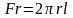
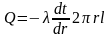
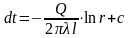

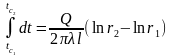

Шчыльнасць:
Падзелим
на l 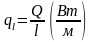
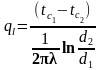
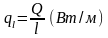
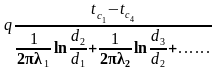
Спрашчэнне разликау цеплаправоднасци праз цылиндрычную сценку.
Разгледзим кали
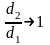
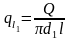
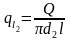
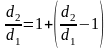
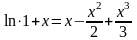 \
\
Пры невяликих х можна написать