ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ
Лекция №2
ПОСТАНОВКА ЗАДАЧИ
Пусть объясняющая переменная X и объясняемая переменная Y
связаны соотношением:
Эта модель является регрессионной, Y=mX+b+ , если MxY=mx+b, т. е. если М =0
где m и b - детерминированные величины, - случайное возмущение.
Получены наблюдения: (x1,y1), (x2,y2), …, (xn,yn). |
|
Требуется по наблюдениям найти в некотором смысле |
|
ˆ |
|
наилучшие оценки mˆ ,b значений m и b. Тогда оценивание Y по |
|
известному x можно производить по формуле: |
|
ˆ |
(*) |
yˆ mˆ x b |
|
Далее дается два подхода к определению таких оценок и формулируются условия, при которых эти подходы дают одинаковый результат.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 
(МНК)
Обозначим: |
|
|
|
|
|
|
|
|
||
yˆ |
mˆx bˆ, e y yˆ |
i |
, |
|
|
|
||||
i |
i |
|
i |
i |
|
|
|
|
||
|
n |
2 |
n |
|
|
2 |
n |
ˆ |
2 |
|
|
|
(yi yˆi ) |
|
|||||||
Qe ei |
|
|
(yi mˆxi b) |
|
||||||
|
i 1 |
|
i 1 |
|
|
|
|
i 1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
yi |
ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yˆi |
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
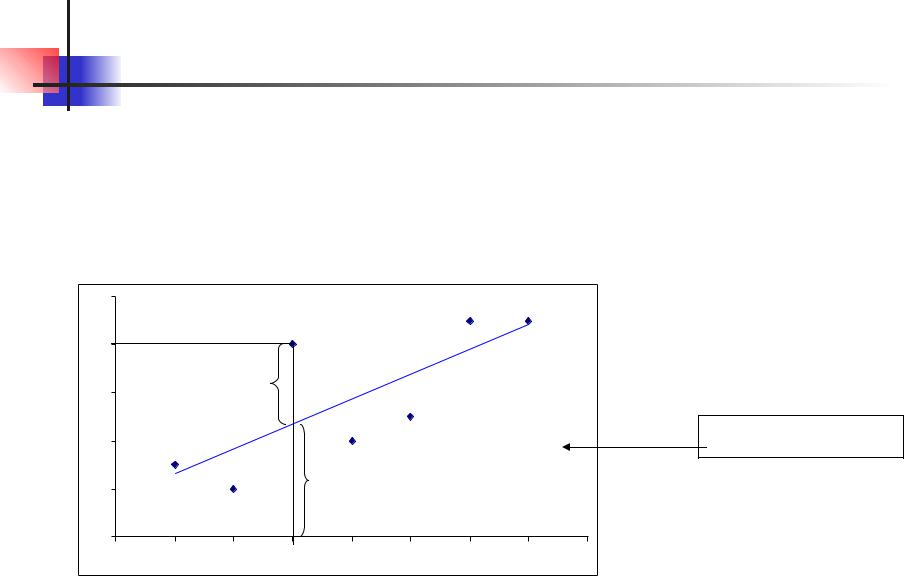
Qe- остаточная сумма
поле корреляции
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
Параметры регрессии определяются из условия минимума остаточной суммы:
n |
ˆ |
2 |
ˆ min |
|
|||
Qe ( yi mˆ xi b) |
|
||
i 1 |
|
|
mˆ ,b |
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
Необходимое условие экстремума: |
|
|||
Qe |
2 |
n |
ˆ |
|
|
ˆ |
( yi b |
||
|
b |
|
i 1 |
|
|
|
|
|
ˆ |
Qe |
2 |
n |
||
|
mˆ |
( yi b |
||
|
|
i 1 |
|
|
mˆ xi ) 0
mˆ xi )xi 0
Откуда получаем нормальную систему уравнений:
|
ˆ |
|
n |
|
|
n |
|
|
bn mˆ |
xi |
yi |
|
|||||
|
|
|
i 1 |
|
i 1 |
(1) |
||
|
ˆ |
n |
n |
|
|
2 |
n |
|
|
|
|
|
|
xi yi |
|
||
b xi mˆ xi |
|
|
||||||
|
|
i 1 |
i 1 |
|
|
i 1 |
|
|
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
Обозначим:
|
|
n |
|
|
|
|
|
|||
|
|
xi |
|
|
|
|
|
|||
x |
i 1 |
|
|
среднее _ значение _ х, |
||||||
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|||
|
|
yi |
|
|
|
|
|
|||
y |
i 1 |
|
среднее _ значение _ y, |
|||||||
|
n |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
__ |
n |
2 |
|
||
__ xi yi |
xi |
|
||||||||
xy |
i 1 |
|
, x2 |
i 1 |
|
|
||||
n |
|
n |
|
|
||||||
|
|
|
|
|
|
|
||||
Тогда из (1) получим:
|
|
ˆ |
|
|
|
|
b mˆ x y |
||
|
ˆ |
__ |
__ (2) |
|
|
|
2 |
xy |
|
bx mˆ x |
|
|||
Решая систему (2), найдем:
__ |
|
|
mˆ xy x y , |
(3) |
|
__ |
||
|
||
x2 x 2 |
|
|
ˆ |
|
|
b y mˆ x. |
|
mˆ - выборочный коэффициент
регрессии
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
|
|
Заметим, что |
|
|
sx-выборочное среднее |
|
|
__ |
|
|
квадратичное отклонение x |
s |
2 |
x2 x2 1 n |
(x x)2- |
|
|
выборочная дисперсия Х |
|||||
|
x |
n i 1 |
i |
|
|
|
|
__ |
n |
(xi x)(yi y) - выборочная |
|
Coˆv(X ,Y ) xy x y 1 |
|||||
|
|
|
n i 1 |
|
ковариация ХиY |
С учетом этих обозначений получим:
|
|
|
|
|
|
|
|
mˆ |
|
Coˆv(X ,Y ) |
|
|
(4) |
|
sx2 |
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
ˆ |
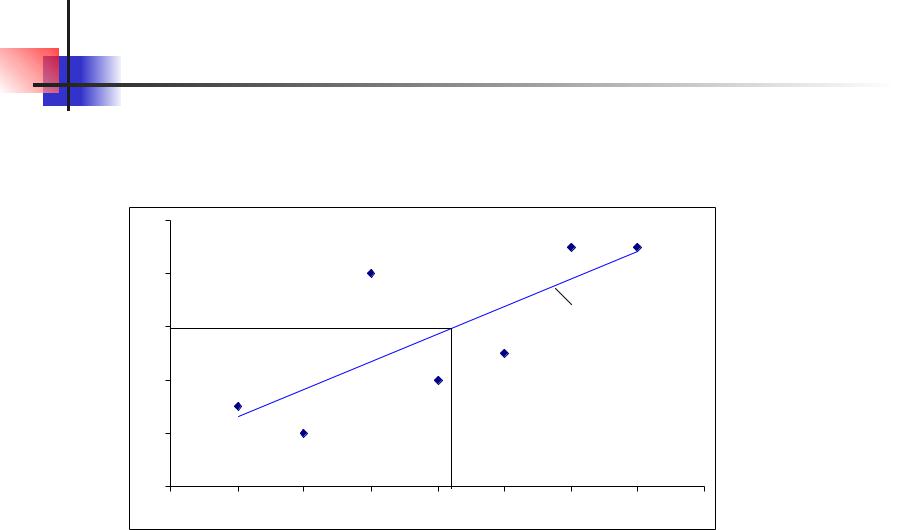
проходит через точку |
(x, y) |
Из (3): прямая y b mˆ x |
||
y |
|
|
(xi,yi) |
ˆ |
|
y |
|
|
y b mˆ x |
|
|
|
x |
x |
|
|
МЕТОД НАИМЕНЬШИХ 
КВАДРАТОВ
При М i=0, i=1,…,n, (отсутствии систематических ошибок)
уравнение y b mx является уравнением регрессии, т. е.
M x y b mx.
Внимание! При получении МНК-оценок параметров b и m
не использовалось никаких предположений о распределении X и Y.
КОЭФФИЦИЕНТ 
КОРРЕЛЯЦИИ
Подставим (3) |
в yˆ |
ˆ |
(*) |
b mˆ x |
yˆ y mˆ x mˆ x yˆ y mˆ (x x)
Представим последнее соотношение в эквивалентном виде:
yˆ y |
mˆ |
sx |
|
x x |
, |
|
|
|
|||
sy |
s y sx |
||||
где sx, sy - выборочные средние квадратичные отклонения x и y.
Здесь используются нормированные и центрированные значения x, y. Нормирование позволяет избежать зависимости от их единиц измерения. Центрирование позволяет работать с приращениями.