
- •Вопрсы к зачету по лин.Ал.У
- •9) Алгебраическая форма комплексного числа
- •Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •14) Извлечение корня из комплексного числа
- •Правило треугольника
- •Правило Саррюса
- •Разложение определителя по строке или столбцу
- •Разложение определителя по строке или столбцу
- •Свойства произведения двух матриц
Свойства произведения двух матриц
1) Произведение матриц ассоциативно (АВ)С = А(ВС) .
2) Для произведения матриц выполняется дистрибутивный закон (А + В) С = АС + ВС , С (А + В) = СА + СВ
3)
Произведение
матриц некоммутативно
![]() .
.
4)Единичная
матрица Е порядка n на n является
нейтральным элементом по умножению, то
есть, для произвольной
матрицы А порядка p на n справедливо
равенство ![]() ,
а для произвольной матрицы А порядка n на p -
равенство
,
а для произвольной матрицы А порядка n на p -
равенство ![]() .
.
5![]() )
Определитель
произведения двух квадратных матриц
равен произведению их определителей:
если С = АВ ,
то .
)
Определитель
произведения двух квадратных матриц
равен произведению их определителей:
если С = АВ ,
то .
23) Для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.
Свойства транспонирования
Д
 важды
транспонированная матрица А равна
исходной матрице А.
важды
транспонированная матрица А равна
исходной матрице А.
Т
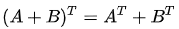 ранспонированная
сумма матриц равна сумме транспонированных
матриц.
ранспонированная
сумма матриц равна сумме транспонированных
матриц.
Т
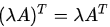 ранспонированное
произведение матриц равно произведению
транспонированных матриц, взятых в
обратном порядке.
ранспонированное
произведение матриц равно произведению
транспонированных матриц, взятых в
обратном порядке.

При транспонировании можно выносить скаляр
О
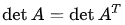 пределитель транспонированной
матрицы равен определителю исходной
матрицы.
пределитель транспонированной
матрицы равен определителю исходной
матрицы.
24) Квадратная матрица А порядка n называется невырожденной, если ее определитель |A| ≠ 0. В случае, когда |A| = 0, матрица А называется вырожденной.
25) Обратной для квадратной матрицы А называется матрица А-1, для которой выполняется: А-1*А=А*А-1=Е, где Е – единичная матрица
Только для квадратных невырожденных матриц А вводится понятие обратной матрицы А-1
Формула обратной матрицы:
 где Aij-
алгебраическое дополнение элементов
aij
где Aij-
алгебраическое дополнение элементов
aij
26) Ранг матрицы А – наивысший порядок отличных от 0 миноров. r(A)
Свойства ранга матрицы:
В матрице размерностью m×n , r(A) ≤ наименьшему из m×n
r(A)=0, если все элементы матрицы = 0
Если матрица А квадратная, порядка n , то r(A) =n когда detA ≠ 0
Ранг матрицы не меняется при ее Элементарных преобразованиях, в этом случае ранг матрицы будет равен количеству не нулевых строк
27) Элементарные преобразования, не меняющие ранг матрицы:
Отбрасывание 0-го столбца (строки)
Перестановка строк (столбцов)
Умножение всех элементов строки (столбца) матрицы на число ≠ 0
Прибавление к каждому элементу одной строки (столбца), соответствующих элементов другой строки (столбца), умноженные на одно и то же число
Транспонирование
28) Основные методы вычисления ранга матрицы:
Метод окаймляющих миноров: пример
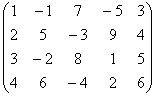
Поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы и, очевидно, что он не превосходит 4. Как действовать дальше?
Дальше
необходимо начать перебор и вычисление
миноров 2-го порядка. Если ВСЕ миноры
2-го порядка окажутся нулевыми, то ранг
матрицы равен единице. Но это крайне
маловероятно, рано или поздно (чаще
всего рано), встретится ненулевой
минор ![]() ,
и данный факт означает, что ранг матрицы не
менее двух.
,
и данный факт означает, что ранг матрицы не
менее двух.
На
следующем шаге последовательно перебираем
и рассчитываем миноры 3-го порядка. Если
ВСЕ эти миноры равны нулю, то ![]() .
Если же встретился минор
.
Если же встретился минор ![]() ,
то делаем вывод о том, что ранг матрицы не
менее трёх и
переходим к следующему шагу.
,
то делаем вывод о том, что ранг матрицы не
менее трёх и
переходим к следующему шагу.
Перебор
и вычисление миноров 4-го порядка. Если
ВСЕ миноры 4-го порядка равны нулю, то ![]() ,
если встретился минор
,
если встретился минор ![]() ,
то
,
то ![]() .
.
Таким образом, ранг матрицы равен максимальному порядку ненулевого минора.
Метод элементарных преобразований
М етод
заключается в том, чтобы с помощь
элементарных преобразований привести
матрицу к треугольному (ступенчатому)
виду. В
этом случае ранг матрицы будет равен
количеству не нулевых строк
етод
заключается в том, чтобы с помощь
элементарных преобразований привести
матрицу к треугольному (ступенчатому)
виду. В
этом случае ранг матрицы будет равен
количеству не нулевых строк
=> r=3
29) Система линейных уравнений

-
называется
квадратной
СЛУ,
если число ![]() уравнений
равно числу
уравнений
равно числу ![]() неизвестных.
Где
неизвестных.
Где
aij – коэффициенты перед неизвестными
(x1, x2 …) – неизвестные
bj – свободный член
30) Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам:

где Δ - определитель матрицы системы, Δi - определитель матрицы системы, где вместо i -го столбца стоит столбец правых частей.
Рассмотрим
систему уравнений 
На
первом шаге вычислим определитель 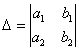 ,
его называют главным
определителем системы.
,
его называют главным
определителем системы.
Если ![]() ,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
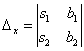 и
и 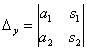
Корни
уравнения находим по формулам:
![]() ,
, ![]()
31)
Матричный
метод

Р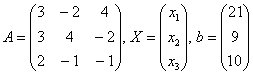 ешение:
Запишем систему в матричной форме:
ешение:
Запишем систему в матричной форме:
![]() ,
где
,
где
Найти
обратную матрицу A
и найти ответ по формуле
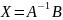
32) Система m-линейных уравнений с n-неизвестной называется система вида:
Где aij – коэффициенты перед неизвестными
(x1, x2 …) – неизвестные
bj – свободный член
33) Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
34) Совместная система называется определенной, если имеет единственное решение и неопределенной, если имеет больше одного решения.
36) Основная матрица системы А – матрица, состоящая из коэффициентов при переменных.
Расширенная матрица системы A˜=(A∣B) - матрица, полученная из матрицы системы A , дописыванием справа после вертикальной черты столбца свободных членов
Теорема Кронекера-Капелли — Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём:
система имеет единственное решение, если ранг равен числу неизвестных; r(A)=r(A*)=n
бесконечное множество решений, если ранг меньше числа неизвестных. r(A)=r(A*)<n
Несовместна, и не имеет ни одного решения, если r(A)≠r(A*)
37) Метод Гаусса - метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
метод Гаусса - идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными. Работает в случае, когда система имеет бесконечно много решений или несовместна.
