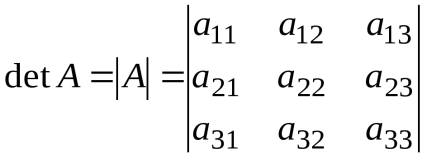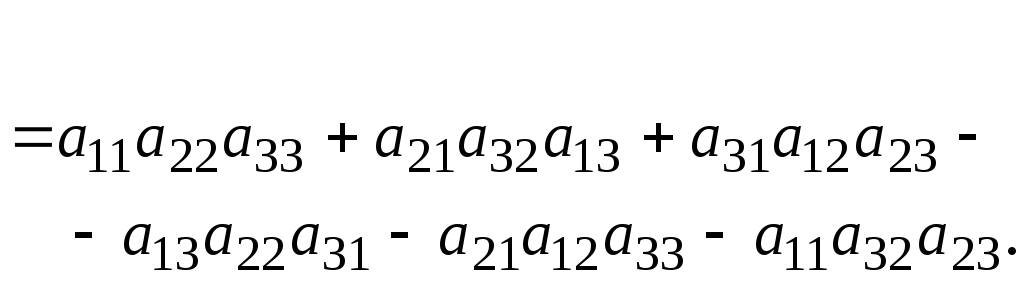Вопрсы к зачету по лин.Ал.У
1)
Комплексное
число (КЧ) Z
-
называют число вида
,
где 
и 
–
действительные числа, 
–
мнимая единица.
Комплексное
число считается записанным корректно,
если записано именно в данном виде.
Запись по типу: 
–
ошибка. Правильный вариант: 
.
2)
Два
комплексных числа
и 
называются равными,
если равны их действительные и мнимые
части, т.е.
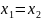и
.
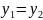В частности КЧ=0, когда x=y=0.
Знаками неравенств КЧ соединить нельзя.
3) 2 КЧ отличающиеся лишь знаком мнимой части называется комплексно-сопряженными
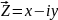для
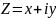
4) Величина угла между положительным направлением действительной оси и вектором R, изображающим КЧ , называется аргументом КЧ ( argZ или 𝞿)
Для
нахождения arg
существует правило
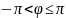
5
) число
–
мнимая
единица,
которая определяется из соотношения
,
при
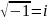
6)
Число
называется
действительной
частью
комплексного числа 
и
имеет обозначение x=ReZ.
Число
называется
мнимой
частью комплексного
числа
и
имеет обозначение y=ImZ.
Если x=0, z=0+iy=iy – чисто мнимое
Если y=0, z=x+io=x –обычно действительное
7) Длина вектора, изображающего комплексное число, называется модулем комплексного числа IZI
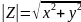
8)
Чтобы изобразить
комплексное число
на
комплексной плоскости необходимо, в
первую очередь, изобразить саму плоскость,
представляющую из себя обычную
координатную плоскость, но с
осями Re (вместо 
)
и Im
(вместо 
),
на первой оси отметить значение
,
на второй – значение
.
Пересечение перпендикуляров к этим
точкам и есть КЧ
.
9) Алгебраическая форма комплексного числа
Запись комплексного числа z в виде z=x+yi, где x и y -действительные числа, называется алгебраической формой комплексного числа.
Например. z=1−i
Тригонометрическая форма комплексного числа
Е
сли
- модуль
комплексного числа 
а ϕ -
его аргумент, то тригонометрической
формой комплексного
числа z называется
выражение
Показательная форма комплексного числа
Показательной
формой комплексного
числа
называется выражение
10)
Для
нахождения arg
существует правило
=> что
:
:
:
:
:
:
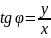
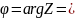
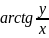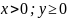
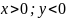
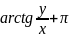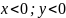
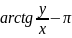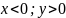
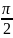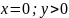
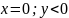
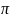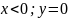
11) Сложение и вычитание комплексных чисел:
В алгебраической форме:
(аналогично
с вычитанием)
В тригонометрической форме:
(аналогично
с вычитанием)
12) Умножение комплексных чисел:
В алгебраической форме:
(простое
раскрытие скобок)
В тригонометрической форме:
Деление комплексных чисел:
В алгебраической форме:
(раскрытие
скобок с помощью домножения знаменателя
на сопряженное)
В тригонометрической форме:
13)
Возведение
комплексного числа в степень 
.
Чтобы возвести КЧ в натуральную степень нужно модуль возвести в степень, а аргумент умножить на показательную степень.
в тригонометрической форме (формула Муавра):
в показательной форме:
14) Извлечение корня из комплексного числа
Чтобы извлечь корень из комплексного числа, в первую очередь, нужно представить его в тригонометрической форме. Количество корней есть значение, равное степени корня. То есть, извлекая корень 4-й степени из комплексного числа, мы получаем 4 корня.
Как и для возведения в целую степень, будет справедливо:
+
–
степень извлекаемого корня, 
.
Вычисляем извлеченные корни поочередно,
в каждый из которых подставляем свое
значение n. Важно помнить, что
аргумент 
и 
должен
находиться в диапазоне 
,
следовательно, нужно не забыть вычесть
нужное количество 
после
всех операций вычисления.
Если
комплексное число не равно нулю, то
корни степени
существуют
всегда, и их можно изобразить на
комплексной плоскости: они будут
представлять собой вершины
правильного
-угольника,
который вписан в окружность с центром
в начале координат и радиусом 
.
15)
Определителем или детерминантом
второго
порядка,
равное разности произведений элементов
стоящих на главной диагонали, и элементов,
стоящих на побочной диагонали (определитель
обозначается 
илиdetA).
Определителем или детерминантом третьего порядка, называется число равное
