3.4. Взаимное расположение двух плоскостей в пространстве. Расстояние от точки до плоскости

Пусть плоскости изаданы общими уравнениями:

, ,

–нормальные векторы этих плоскостей соответственно.

Плоскости ипараллельны или совпадают тогда и только тогда, когда векторыколлинеарны. Записывая условие коллинеарности векторов (2.6), получаем: еслито плоскости параллельны; еслито плоскости совпадают.

Если же координаты векторов не пропорциональны, то плоскости пересекаются по некоторой прямойl. Очевидно, что

.

Отсюда получаем условие перпендикулярности плоскостей

.

Как и для двух прямых на плоскости можно вывести следующую формулу:

,

где – один из смежных двугранных углов между плоскостями. Расстояние d от точки М₀(х₀, у₀, z₀) до плоскости вычисляется по формуле:

Пример 3.5. Составить уравнение плоскости , проходящей через точкуM₁(–1, 2, 5) параллельно плоскости :.

Решение. Нормальный вектор ={2, –3, 0} плоскостиявляется также нормальным вектором плоскости. Используя равенство (3.11) получаем:

– уравнение плоскости по точке и нормальному вектору. Раскрывая скобки и приводя подобные слагаемые, найдем– общее уравнение плоскости.

3.5. Уравнения прямой в пространстве

Прямую линию в пространстве можно задать как пересечение двух плоскостей. Рассмотрим систему двух уравнений:

. (3.14)

Каждое из уравнений определяет в пространстве плоскость. Если коэффициенты при переменных x, у, z не пропорциональны, то эти плоскости пересекаются по некоторой прямой l. Координаты любой точки удовлетворяют системе (З.14) тогда и только тогда, когда точка лежит на прямой l. Поэтому уравнения (3.14) являются уравнениями прямой l и называются общими уравнениями прямой.

Итак, прямая в пространстве задается двумя линейными уравнениями.

Выведем другие виды уравнений прямой в пространстве.

Пусть задана точка М₁(х₁, у₁, z₁), лежащая на прямой l и ее направляющий вектор . ПустьM(x, y, z) произвольная точка прямой l, тогда векторы иколлинеарны и по формуле (2.6) получаем:

(3.15)

– канонические уравненияпрямойl(уравнения прямой по точке и направляющему вектору). Из канонических уравнений, введя параметрt(коэффициент пропорциональности), который может принимать любые действительные значения:

получаем параметрические уравнения прямой l:

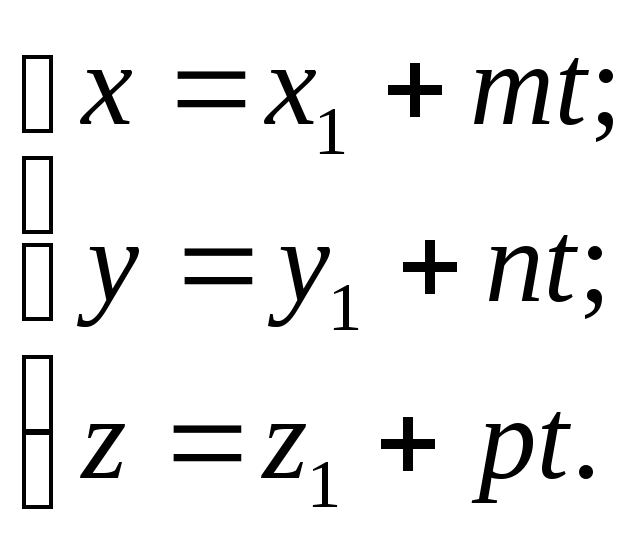
При изменении параметра t координаты точки М(х, у, z) изменяются и она перемещается по прямой l.

Заметим, что для прямой на плоскости можно вывести аналогичные параметрические уравнения:

Уравнения прямой, проходящей через две заданные точки (уравнения прямой по двум точкам) М₁(х₁, у₁, z₁) и М₂(х₂, у₂, z₂), предлагается вывести самостоятельно, они имеет вид:

Рассмотрим переход от общих уравнений прямой к параметрическим.

Пусть прямая l задана уравнениями (3.14), т.е. является линией пересечения плоскостей и, которые имеют нормальные векторы:

= {A₁, B₁, C₁} и = {A₂, B₂, C₂}

(рис. 3.14). Запишем канонические уравнения прямой l. Для этого из системы (3.14) найдем одно решение (х₁, у₁, z₁) – координаты точки М₁(х₁, у₁, z₁), лежащей на l (система (3.14) имеет бесконечное множество решений). Поскольку

,

поэтому вектор параллелен прямойl, следовательно, – направляющий векторl. Координаты вектора найдем по формуле (2.10), вычислив векторное произведение:

Подставив найденные числа в уравнения (3.15), получим канонические уравнения прямой l.

Пример 3.6. Прямая l является пересечением плоскостей:

: 2х – у + z – 4 = 0 и :х + у – 2z – 1 = 0.

Найти канонические уравнения прямой l.

Решение. 1) Решим систему уравнений:

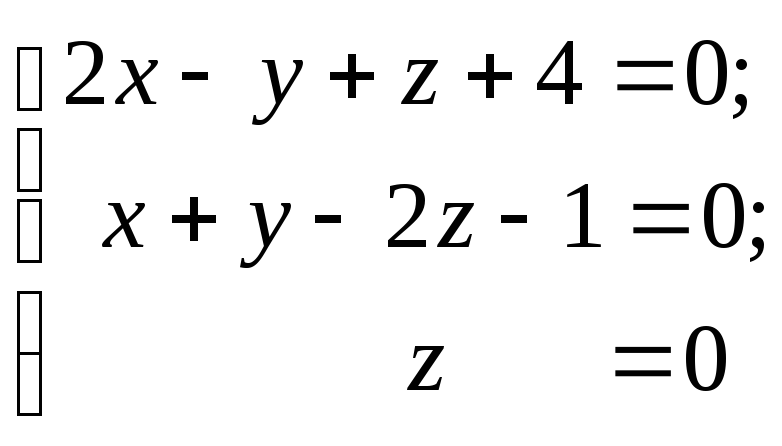
получим тройку чисел (–1, 2, 0) – точку пересечения прямой l с координатой плоскостью 0ху.

2) Найдем направляющий вектор прямой l:

Подставляя полученные данные в уравнения (3.15), находим:

канонические уравнения прямой l.