Контрольные вопросы

1. Дать определение:

   1. замкнутой системы,

   2. импульса тела,

   3. удара, упругого и неупругого ударов,

   4. центрального прямого удара.

2. Сформулировать закон сохранения импульса системы тел и дать его математическую запись.

3. Получить уравнения (8.7) и (8.8).

4. Какой удар (упругий или неупругий) имеет место в следующих случаях:

5. пуля застряла в бруске,

6. мяч отскочил от стены,

7. вратарь в прыжке поймал мяч,

8. биллиардный шар ударил другой так, что оба влетели в две разные лузы.

5. Будет ли удар в последнем случае центральным?

Цикл 3. Динамика вращательного движения.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Лабораторная работа 9

ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Цели работы: проверить зависимость углового ускорения от момента силы при постоянном моменте инерции и представить эту зависимость графически; определить момент инерции маятника Обербека.

Приборы и принадлежности: маятник Обербека, штангенциркуль, секундомер, набор грузов, технические весы с разновесом.

Библиографический список: [1] § 16–19; [2] ч.1 § 21–23; [3] т.1 § 38–39, § 41;[4] т.1 § 10 - 11;[5] § 2.10, § 5.1, § 5.3–5.4; § 5.11; [7] § 1.3.3.

Введение

В

Рис. 9.1.

ращательным движениемабсолютно твердого тела называется движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, с центром, расположенным на прямой, называемойосью вращения.

Д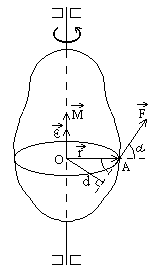ля описания вращательного движения вводят следующие величины: момент силы, момент инерции, момент импульса.Моментом силыотносительно неподвижной точки О (рис. 9.1) называется векторная величина, равная векторному произведению радиус-вектора, проведенного из точки О в точку приложения силы, на вектор силы:

. (9.1)

Модуль вектора равен:

, (9.2)

где α – угол между направлениями векторов и, аd=rsinα – длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила (рис. 9.1). Эта длина называетсяплечом силыотносительно точки О.

Моментом инерции I материальной точкиотносительно оси вращения называется физическая величина, равная произведению массыmточки на квадрат ее расстоянияrдо оси вращения:

I = m·r². (9.3)

Моментом инерции телаотносительно неподвижной оси вращения называется сумма моментов инерции всех материальных точек, составляющих тело:

. (9.4)

Момент инерции характеризует инертные свойства вращающегося тела и зависит от распределения массы в теле, расположения оси вращения, формы тела.

Моментом импульсаматериальной точки относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-векторана вектор импульса:

. (9.5)

Учитывая, что импульс материальной точки равен , получим еще одно выражение для момента импульса:

, (9.6)

где ω– угловая скорость материальной точки.

Основное уравнение динамики вращательного движения(или второй закон Ньютона для вращательного движения) в дифференциальной форме имеет вид:

, (9.7)

здесь – суммарный (результирующий) момент внешних сил относительно произвольного центра вращения О,– момент импульса твердого тела относительно этого же центра.

Если момент инерции тела относительно фиксированной оси вращения остается величиной постоянной, то уравнение (9.7) можно записать в виде:

, (9.8)

где М_z– проекция векторана ось вращения, проходящую через точку О (или момент силы относительно оси вращения),I_z– момент инерции относительно этой же оси,ε– угловое ускорение вращающегося тела.