Изменение логической функцииY.
В исходной схеме представлена логическая функция Y= (RAилиRB). Применены 8 логических элементов 2ИЛИ. Новая логическая функция имеет вид:Y= -RA+RB-SA. Как видим, операция ИЛИ нам не требуется, поэтому можем смело удалить всю исходную логическую функцию. Новая функция имеет операции суммирования и вычитания, что потребует применения сумматоров. Однако сумматоры это громоздкие элементы, поэтому всю схему разместим на отдельном листе и будем отлаживать отдельно от исходной схемы.
Числа RA,RBиSA, над которыми и проводится операция вычисления результата функцииY– примем положительными, так как в задании не упоминается наличие старшего знакового бита у исходных значений. Это значит, что результирующее числоYможет иметь пределы от -510 (RA= 255,SA= 255,RB= 0), до 255 (RA= 0,SA= 0,RB= 255). Из этого следует, что необходимо применить либо 10 разрядный сумматор, со старшим (9-ым) знаковым битом и с битом переполнения результата (бит 8), либо использовать 8 разрядный, а знаковый бит и бит переполнения генерировать, используя биты переполнения сумматора. Используем 2-й метод, так как он не требует расширения шины сумматоров и экономит пространство ПЛИС.
Использование 2-х сумматоров, с двумя операндами каждая, на выходе даст либо положительный, либо отрицательный результат. Отрицательный результат на выходе сумматора будет представлен либо обратным, либо дополнительным кодом, что на шине данных будет иметь непонятный результат (например Y= -12 на шине данных будет либо 243 для обратного кода, либо 244 для дополнительного кода). Для перевода результата в прямой код применим дополнительный сумматор. Положительное значение на выходе будет представлено истинным значением, поэтому изменений не требует. Знак и наличие переполнения будем определять применяя логические элементы «И ИЛИ», а результаты выведем как отдельные выходные линии. Полученная схема вычисления результата функцииYпредставлена на рисунке 9. Рассмотрим подробнее элемент «сумматор» и работу схемы в целом.
Рисунок 9. Схема вычисления результата функции Y.
Сумматор. Представляет собой HDL код, сформированный в виде графического элемента. Имеет множество входов, выходов, а также управляющих параметров. Входные линии представлены в таблице 3, выходные – в таблице 4, а управляющие параметры – в таблице 5.
Таблица 3. Входные линии.
|
Линия |
Необходим |
Описание |
Комментарии |
|
cin |
Нет |
Перенос к биту младшего разряда |
Если не указан, то принимается равным 0. |
|
dataa[] |
Да |
Первое слагаемое |
Шина данных с разрядностью LPM_WIDTH |
|
datab[] |
Да |
Второе слагаемое |
Шина данных с разрядностью LPM_WIDTH |
|
add_sub |
Нет |
Если == 0, то выполнится: DA + DB + cin. Если == 1, то выполнится: DA – DB + cin - 1 |
Если не указан, принимается равным 0. Не применять совместно с LPM_DIRECTION. |
|
clock |
Нет |
Синхронизация |
Вход синхронизации для конвейерных операция. Вход должен быть подключен к линии синхронизации, если LPM_PIPELINE имеет значение, отличное от 0. |
|
clken |
Нет |
Разрешение clock |
Если не указан, принимается равным 1. |
|
aclr |
Нет |
Асинхронный сброс для конвейерных операций. |
Конвейер инициализируется неопределенным значением. Сброс к нулевым значениям можно произвести в любой момент времени. |
Таблица 4. Выходные линии.
|
Линия |
Необходим |
Описание |
Комментарии |
|
result[] |
Да |
Результат вычисления |
Шина данных с разрядностью LPM_WIDTH |
|
cout |
Нет |
Перенос со старшего разряда. |
Если overflow используется, не применять. Применяется в основном при беззнаковых операциях. |
|
overflow |
Нет |
Результат превысил максимальное значение |
Если cout используется, не применять. Применяется в основном при знаковых операциях. |
Таблица 5. Конфигурационные параметры.
|
Линия |
Необходим |
Комментарии |
|
LPM_WIDTH |
Да |
Разрядность входных и выходных шин данных |
|
LPM_DIRECTION |
Нет |
Значения «ADD», «SUB» или «UNUSED». По умолчанию – «DEFAULT». Если DEFAULT, то используется значение add_sub. |
|
LPM_REPRESENTATION |
Нет |
Тип входных значений: «SIGNED» или «UNSIGNED». По умолчанию – SIGNED. |
|
LPM_PIPELINE |
Нет |
Задержка в тактах перед получением результата result[]. По умолчанию 0. |
|
ONE_INPUT_IN_CONSTANT |
Нет |
Принимает значения: «YES», «NO» и «UNUSED». Позволяет оптимизировать генерируемый код в случае применения констант. По умолчанию NO. |
|
MAXIMIZE_SPEED |
Нет |
Задает способ оптимизации кода в сторону скорости, либо использованной области. Переопределяет значение «Optimize», задаваемое в меню. |
Настроим сумматоры. Сконфигурируем сумматор со следующими параметрами:
|
LPM_WIDTH: |
8 |
|
LPM_DIRECTION: |
DEFAULT |
|
LPM_REPRESENTATION: |
UNSIGNED |
|
LPM_PIPELINE: |
<none> |
|
ONE_INPUT_IN_CONSTANT: |
<none> |
|
MAXIMIZE_SPEED: |
<none> |
Как видно, мы задали входные данные восьмиразрядными беззнаковыми, что и требовалось по заданию. А LPM_DIRECTIONзададим извне, с использованием входаadd_sub. Такой выбор обоснован прежде всего учебным характером задания, то есть нет необходимости оптимизировать код.
Сконфигурируем выходные линии (укажем используемые выходы):
|
result[]: |
Да |
|
cout: |
Нет |
|
overflow: |
Да |
Хоть и в описании указано, что overflow не рекомендуется применять с беззнаковыми числами, все же мы применим именно его, так как он нам дает более удобные значения, нежели cout.
Cконфигурируем входные линии, а именно зададим используемость входов:
|
cin: |
Да |
|
dataa[]: |
Да |
|
datab[]: |
Да |
|
add_sub: |
Да |
|
clock: |
Нет |
|
clken: |
Нет |
|
aclr: |
Нет |
Кроме обязательных входов дополнительно применим входы cinиadd_sub. С помощьюadd_subбудем управлять выполняемой сумматором операцией, аcinпозволит нам задавать тип кода: обратный либо дополнительный. (Обратный код – отрицательные числа побитово инвертируются, а положительные не меняются. Дополнительный код – отрицательные числа побитово инвертируются, затем добавляется «1» к результату, положительные числа не меняются). Как известно, обратный код требует прибавления к результату операции переноса со старшего разряда, если таковой имеется, поэтому применим дополнительный код. Выполняемая операция будет выглядеть следующим образом:
В зависимости от значения add_subпроизойдет сложение прямого либо обратного кодаBи прибавлениеcin. Если сложение, тоcinдолжен быть равен «0», а если вычитание, тоcinдолжен равняться «1».
На рисунке 9 видно, что 2 сумматора имеют «0» на входе add_sub, и «1» на входеcin, из чего следует, что результат будет представлен в дополнительном коде и выглядит как (A-B)-C.
Результат получен, он представляет из себя восьмиразрядное значение в дополнительном коде. Чтобы его перевести в понятный прямой код, необходимо определить знак, и если он отрицательный, вычесть результат из 0 той же разрядности. Поэтому добавим в схему дополнительный сумматор, выполняемой операцией которого будет управлять комбинационная схема определения знака результата функции. А константу 0 будем подавать от отдельного устройства LPM_CONSTANT.
Осталось
определить знак результата и наличие
переполнения (результат меньше «-255»).
Значение на выходе overflowподчиняется формуле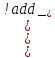
.coutдля положительных
чисел == 1 только когдаA+B>= 256, для отрицательных == 1 – только
когдаA-B>=0.
Из этого следует, чтоoverflowдля положительных чисел == 1 только когдаA+B>= 256, а
для отрицательных – только когдаA-B< 0.
Наличие overflowлибо при первом, либо при втором вычитании позволит судить об отрицательности результата, а еслиoverflowесть и при первом, и при втором вычитании, значит произошло переполнение разрядной сетки операнда.
Покажем все это на примерах.
Пример 1: Y= 2 – 1(вычитание в дополнительном коде, результат положительный):
|
+ |
00000010 |
Операнд A(2). |
|
11111111 |
Операнд B (-1) [not B + cin]. | |
|
|
100000001 |
Результат, имеется перенос. |
Результат положительный (имеется перенос), в прямом коде. Наличие переноса сформирует на выходе overflowлогический «0».
Пример 2: Y= 2 – 2 (вычитание в дополнительном коде, результат равен нулю):
|
+ |
00000010 |
Операнд A(2). |
|
11111110 |
Операнд B (-2) [not B + cin]. | |
|
|
100000000 |
Результат, имеется перенос. |
Результат положительный (имеется перенос), в прямом коде. Наличие переноса сформирует на выходе overflowлогический «0».
Пример 3: Y= 1 – 2 (вычитание в дополнительном коде, результат отрицательный):
|
+ |
00000001 |
Операнд A(1). |
|
11111110 |
Операнд B (-2) [not B + cin]. | |
|
|
11111111 |
Результат, переноса нет. |
Результат отрицательный (переноса нет), в дополнительном коде. Наличие переноса сформирует на выходе overflowлогическую «1».
Пример 4: Y= -255 – 2 (первый сумматор дал отрицательный результат):
|
+ |
00000001 |
Операнд A(-255). |
|
11111110 |
Операнд B (-2) [not B + cin]. | |
|
|
11111111 |
Результат (-1), переноса нет. |
Результат отрицательный, наличие переноса текущего и предыдущего вычитаний говорит о переполнении разрядной сетки, и об отрицательном знаке результата.