
04
.doc
|
К
|
К |
|
К2.2
|
К |
|
К
|
К |
|
К2.6
|
К |
|
К2.8
|
К |
Таблица К2
|
№ |
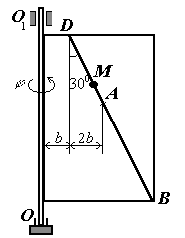
Для всех рисунков
|
Для рис. К2.0 – К2.4 |
Для рис. К2.5 – К2.9 |
||
|
см |
|
|
|
||
|
0 |
|
12 |
|
|
|
|
1 |
|
16 |
|
|
|
|
2 |
|
10 |
|
|
|
|
3 |
|
16 |
|
|
|
|
4 |
|
8 |
|
|
|
|
5 |
|
20 |
|
|
|
|
6 |
|
12 |
|
|
|
|
7 |
|
8 |
|
|
|
|
8 |
|
10 |
|
|
|
|
9 |
|
20 |
|
|
|
на пластине в
момент времени
![]() с,
и изобразить точку именно в этом положении
(а не в произвольном, показанном на
рисунках к задаче).
с,
и изобразить точку именно в этом положении
(а не в произвольном, показанном на
рисунках к задаче).
В случаях, относящихся
к рис. К2.5 – К2.9 , при решении задачи не
подставлять числового значения R,
пока не будут определены положение
точки М
в момент времени
![]() с
и угол между радиусами СМ
и СА
в этот момент.
с
и угол между радиусами СМ
и СА
в этот момент.
Рассмотрим два примера решения этой задачи.
Пример К2а.
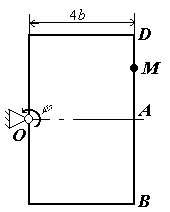
Пластина
ОЕАВ1D
(ОЕ = ОD,
рис. К2а) (ОЕ
= ОД,
рис. К2а) вращается вокруг оси, проходящей
через точку О
перпендикулярно плоскости пластины,
по закону
![]() (положительное направление отсчета
угла
(положительное направление отсчета
угла
![]() показано на рис. К2а дуговой стрелкой).
По дуге окружности радиуса R
движется точка В по закону
показано на рис. К2а дуговой стрелкой).
По дуге окружности радиуса R
движется точка В по закону
![]() (положительное направление отсчета s
– от А
к В).
(положительное направление отсчета s
– от А
к В).
Д а н о: R=0,5
м,
![]() (
(![]() - в радианах, s
– в метрах, t
– в секундах).
- в радианах, s
– в метрах, t
– в секундах).
О п р е д е л и т ь:
![]() и
и
![]() в момент времени
в момент времени
![]() с.
с.
Решение.
Рассмотрим
движение точки В как сложное, считая ее
движение по дуге окружности относительным,
а вращение пластины - переносным
движением. Тогда абсолютная скорость
![]() и абсолютное ускорение
и абсолютное ускорение
![]() точки найдутся по формулам:
точки найдутся по формулам:
![]() ,
,
![]() (1)
(1)
где, в свою очередь,
![]()
![]()
О пределим
все, входящие в равенства (1) величины.
пределим
все, входящие в равенства (1) величины.
Рис. К2а
-
О т н о с и т е л ь н о е д в и ж е н и е. Это движение происходит по
закону
![]() .
(2)
.
(2)
Сначала установим,
где будет находиться точка В
на дуге окружности в момент времени
![]() .
Пологая в уравнении (2)
.
Пологая в уравнении (2)
![]() с, получим
с, получим
![]()
![]()
Тогда![]()
![]()
Знак минус
свидетельствует о том, что точка В
в момент
![]() с находится справа от точки А.
Изображаем ее на рис. К2а в этом положении
(точка В1).
с находится справа от точки А.
Изображаем ее на рис. К2а в этом положении
(точка В1).
Теперь находим
числовые значения
![]() :
:
![]()
![]()
![]() ,
,
где
![]() - радиус кривизны относительной
траектории, равный радиусу окружности
R.
Для момента
- радиус кривизны относительной
траектории, равный радиусу окружности
R.
Для момента
![]() с, учитывая, что R
= 0,5 м, получим
с, учитывая, что R
= 0,5 м, получим
![]() м/c,
м/c,
![]() м/c2,
м/c2,
![]() м/с2.
(3)
м/с2.
(3)
Знаки показывают,
что вектор
![]() направлен в сторону положительного
отсчета расстояния
направлен в сторону положительного
отсчета расстояния
![]() а вектор
а вектор
![]() - в противоположную сторону; вектор
- в противоположную сторону; вектор
![]() направлен к центру С
окружности. Изображаем все эти векторы
на рис. К2а.
направлен к центру С
окружности. Изображаем все эти векторы
на рис. К2а.
-
П е р е н о с н о е д в и ж е н и е. Это движение (вращение) происходит по закону
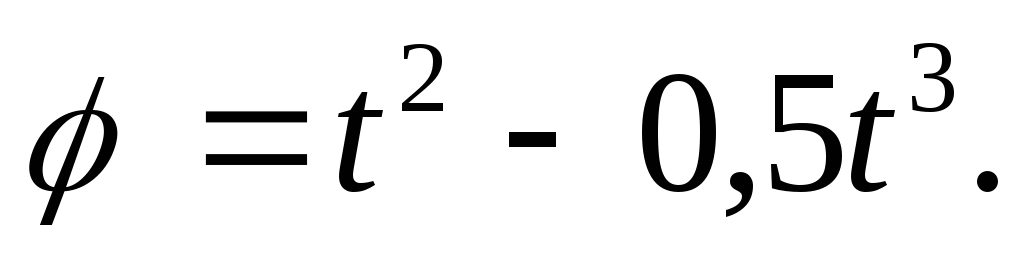 Найдем сначала угловую скорость
Найдем сначала угловую скорость
 и угловое ускорение
и угловое ускорение
 переносного вращения:
переносного вращения:
![]()
и при
![]() с
с
![]() с-1,
с-1,
![]() с-1.
(4)
с-1.
(4)
Знаки указывают,
что в момент
![]() с направления
с направления
![]() и
и
![]() противоположны направлению положительного
отсчета угла
противоположны направлению положительного
отсчета угла
![]() ;
отметим это на рис. К2а.
;
отметим это на рис. К2а.
Для определения
![]() и
и
![]() находим сначала расстояние
находим сначала расстояние
![]() ОВ1
точки В1
от оси вращения О.
Из рисунка видно, что
ОВ1
точки В1
от оси вращения О.
Из рисунка видно, что
![]() м. Тогда в момент времени
м. Тогда в момент времени
![]() с , учитывая равенства (4), получим
с , учитывая равенства (4), получим
![]() м/c,
м/c,
![]() м/с2,
м/с2,
![]() м/c2.
(5)
м/c2.
(5)
Изображаем на рис.
К2а векторы
![]() и
и
![]() с
учетом направлений
с
учетом направлений
![]() и
и
![]() и
вектор
и
вектор
![]() (направлен к оси вращения).
(направлен к оси вращения).
-
К о р и о л и с о в о у с к о р е н и е. Модуль кориолисова ускорения определяем по формуле
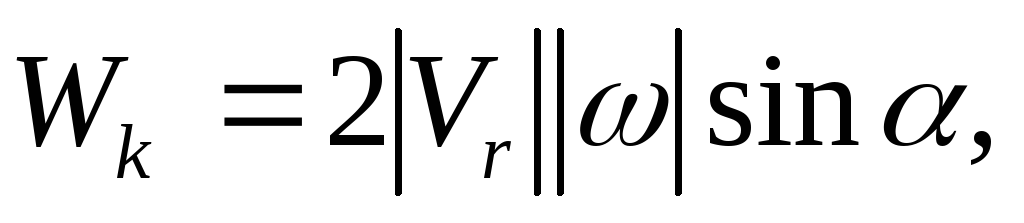 где
где
 - угол между вектором
- угол между вектором
 и осью вращения (вектором
и осью вращения (вектором
 ).
В нашем случае этот угол равен 900
, так как ось вращения перпендикулярна
плоскости пластины, в которой расположен
вектор
).
В нашем случае этот угол равен 900
, так как ось вращения перпендикулярна
плоскости пластины, в которой расположен
вектор
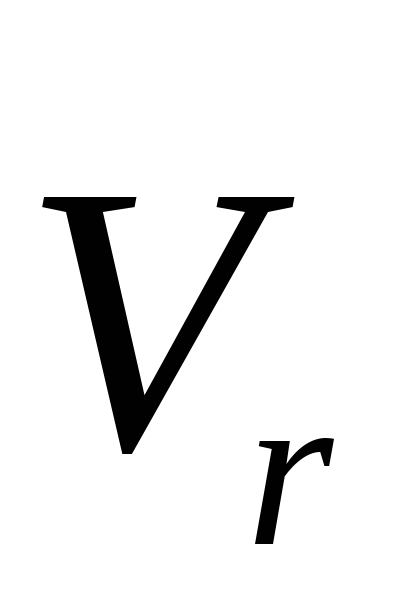 .
Численно в момент времени
.
Численно в момент времени
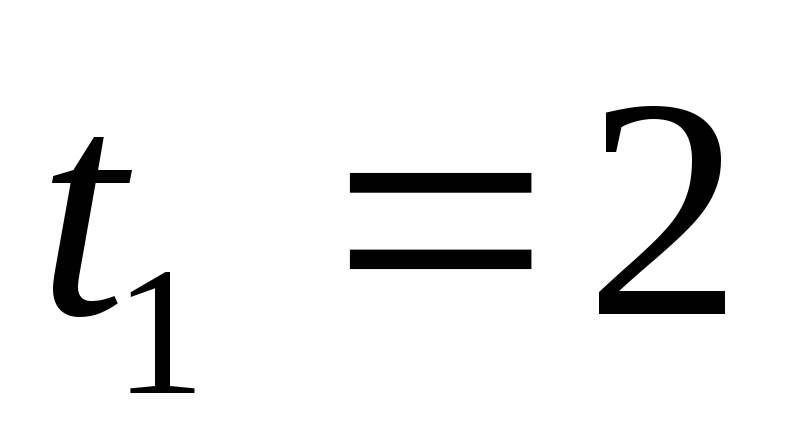 с, так как в этот момент
с, так как в этот момент
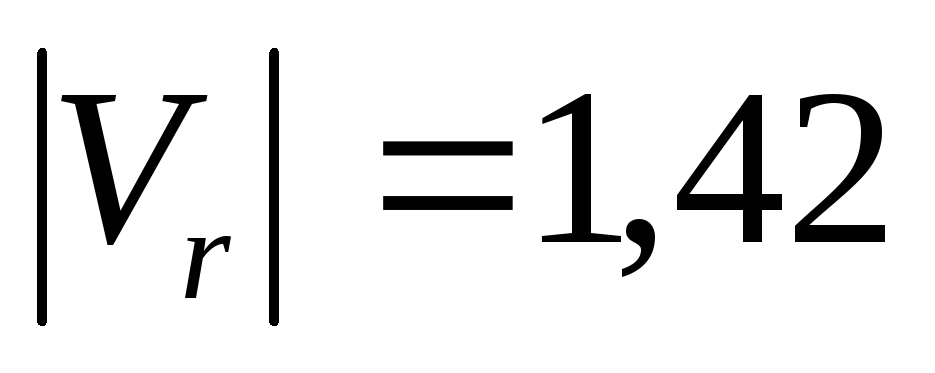 м/c
и
м/c
и
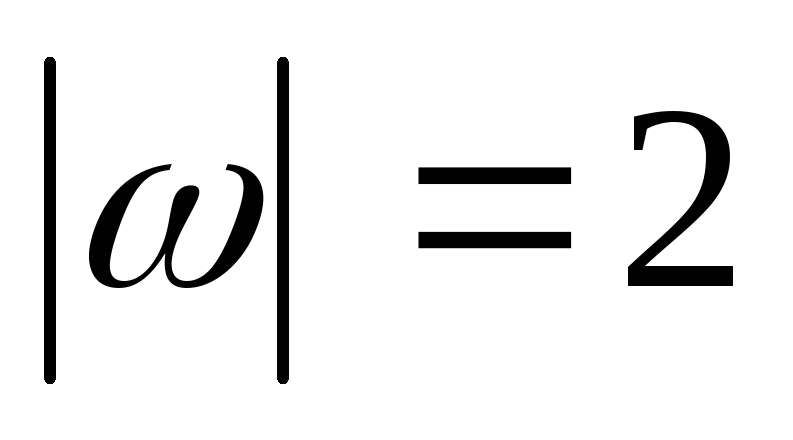 с-1,
получим
с-1,
получим
![]() м/c2.
(6)
м/c2.
(6)
Направление
![]() найдем по правилу Н.Е.Жуковского: так
как вектор
найдем по правилу Н.Е.Жуковского: так
как вектор
![]() лежит в плоскости, перпендикулярной
оси вращения, то повернем его на 900
в направлении
лежит в плоскости, перпендикулярной
оси вращения, то повернем его на 900
в направлении
![]() ,
т. е. по ходу часовой стрелки. Изображаем
,
т. е. по ходу часовой стрелки. Изображаем
![]() на рис. К2а. (Иначе направление
на рис. К2а. (Иначе направление
![]() можно найти, учтя, что
можно найти, учтя, что
![]() .)
.)
Таким образом,
значения всех входящих в правые части
равенств (1) векторов найдены и для
определения
![]() и
и
![]() остается только сложить эти векторы.
Произведем это сложение аналитически.
остается только сложить эти векторы.
Произведем это сложение аналитически.
-
О п р е д е л е н и е
 .
Проведем координаты оси В1
.
Проведем координаты оси В1
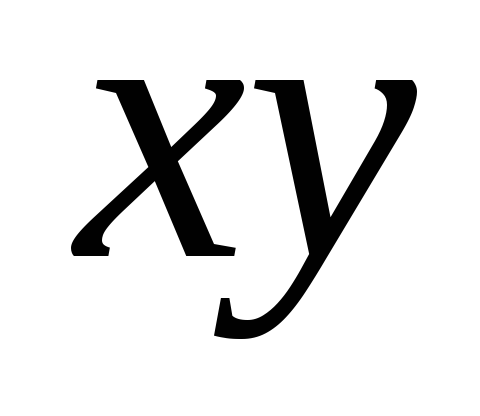 (см. рис. К2а) и спроектируем почленно
обе части равенства
(см. рис. К2а) и спроектируем почленно
обе части равенства
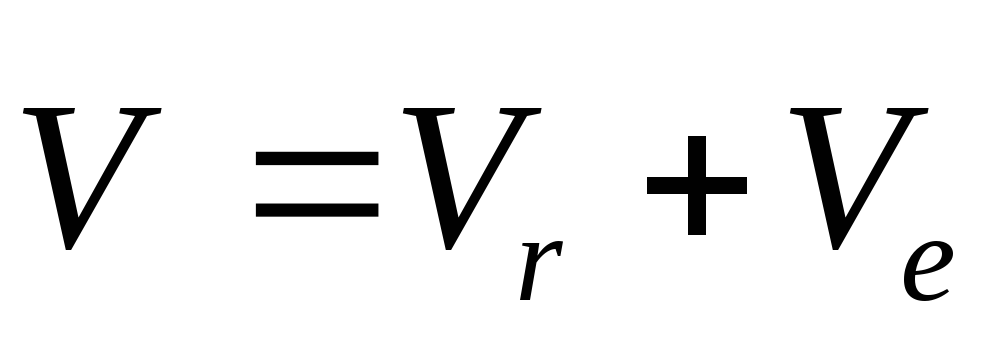 на эти оси. Получим для момента времени
на эти оси. Получим для момента времени
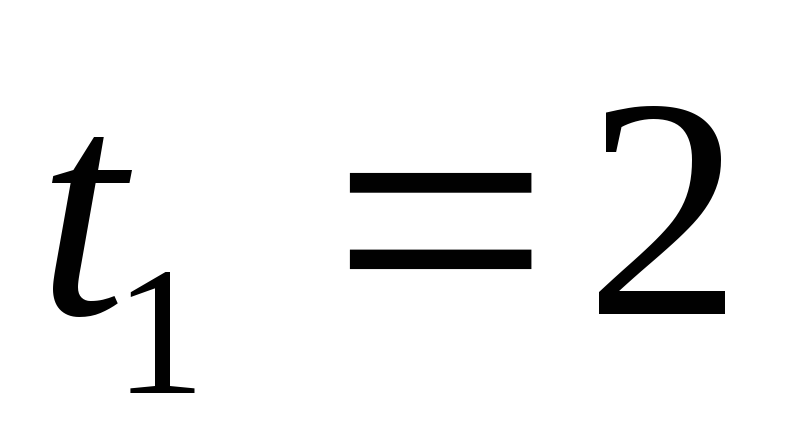 с:
с:
![]() м/c;
м/c;
![]() м/с;
м/с;
После этого находим
![]() м/c.
м/c.
Учитывая, что в
данном случае угол между
![]() и
и
![]() равен 450
, значение
равен 450
, значение
![]() можно еще определить по формуле
можно еще определить по формуле
![]() м/c.
м/c.
-
О п р е д е л е н и е
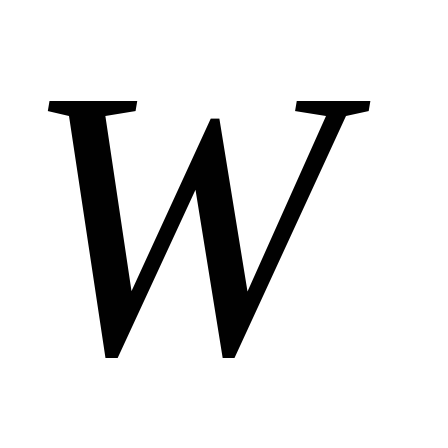 .
По теореме о сложении ускорений
.
По теореме о сложении ускорений
![]() (7)
(7)
Для определения
![]() спроектируем обе части равенства (7) на
спроектируем обе части равенства (7) на
![]() проведенные
оси В1
проведенные
оси В1![]() .
Получим
.
Получим
![]()
Подставив сюда
значение, которые все величины имеют в
момент времени
![]() с, найдем, что в этот момент
с, найдем, что в этот момент
![]() м/с2;
м/с2;
![]() м/c2.
м/c2.
Тогда
![]() м/c2.
м/c2.
О т в е т:
![]() м/c,
м/c,
![]() м/c2.
м/c2.
Пример К2б.
Треугольная
пластина АDE
вращается вокруг оси
![]() по закону
по закону
![]() (положительное
направление отчета угла
(положительное
направление отчета угла
![]() показано на рис. К4б дуговой стрелкой).
По гипотенузе AD
движется точка B
по закону
показано на рис. К4б дуговой стрелкой).
По гипотенузе AD
движется точка B
по закону
![]() положительное направление отчета
положительное направление отчета
![]() от А
к D.
от А
к D.
Д а н о:
![]()
![]() (
(![]() в
радианах,
в
радианах,
![]() в сантиметрах,
в сантиметрах,
![]() в секундах).
в секундах).
О п р е д е л и т ь:
![]() и
и
![]() в момент времени
в момент времени
![]() с.
с.
Решение.
Рассмотрим
движение точки В как сложное, считая ее
движение по прямой AD
относительным, а вращение пластины -
переносным. Тогда абсолютная скорость
![]() и абсолютное ускорение
и абсолютное ускорение
![]() найдутся по формулам:
найдутся по формулам:
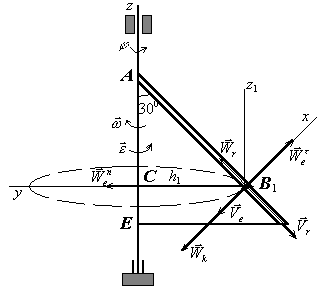
Рис. К2б
![]() ,
,
![]() ,
(1)
,
(1)
где, в свою очередь,
![]()
-
О т н о с и т е л ь н о е д в и ж е н и е. Это движение прямолинейное и происходит по закону
![]() .
(2)
.
(2)
![]()
![]()
поэтому в момент
времени
 с имеем
с имеем
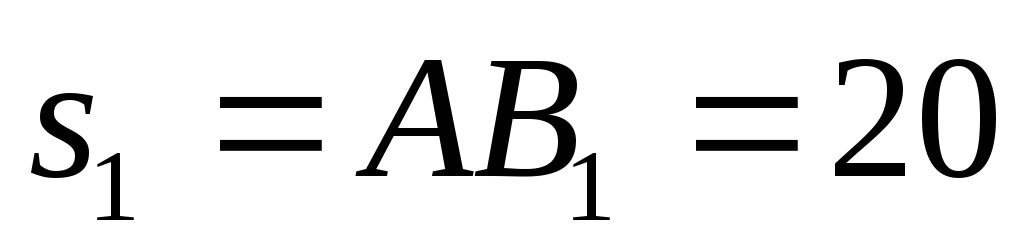 см,
см,
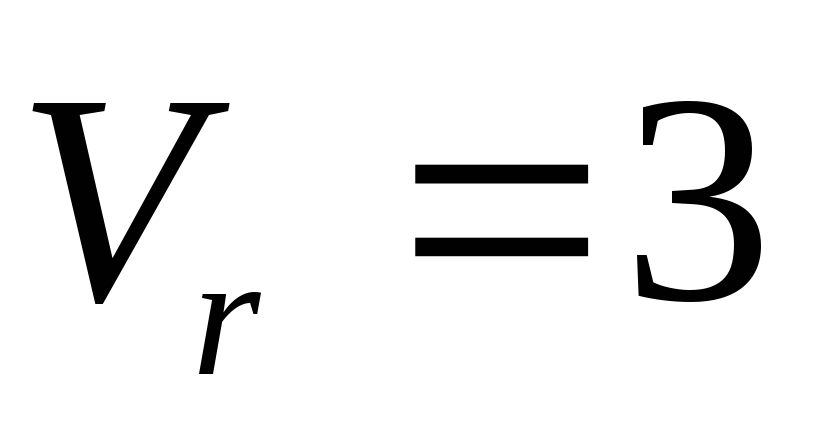 см/с,
см/с,
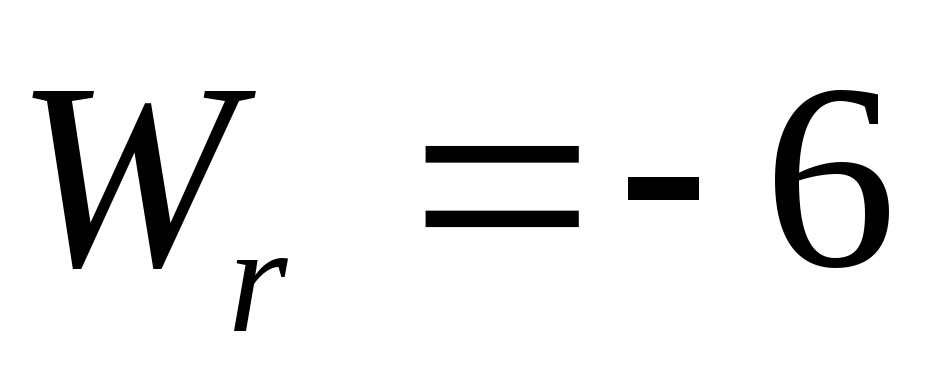 см/с2
(6)
см/с2
(6)
Знаки показывают,
что вектор
![]() направлен в сторону положительного
отсчета расстояния
направлен в сторону положительного
отсчета расстояния
![]() ,
а вектор
,
а вектор
![]() в противоположную сторону. Изображаем
эти векторы на рис. К2б.
в противоположную сторону. Изображаем
эти векторы на рис. К2б.
-
П е р е н о с н о е д в и ж е н и е. Это движение (вращение) происходит по закону
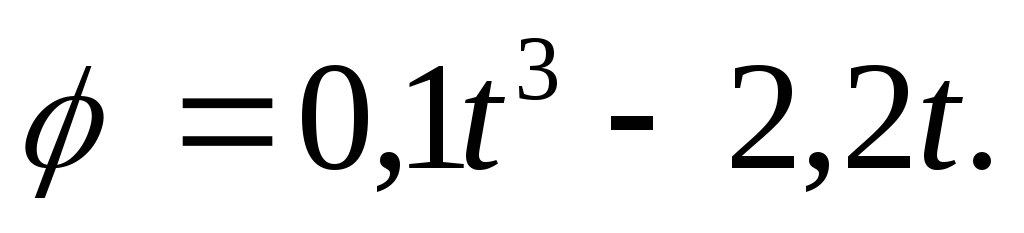
Найдем угловую
скорость
![]() и угловое ускорение
и угловое ускорение
![]() переносного вращения:
переносного вращения:
![]()
![]() и при
и при
![]() с,
с,
![]() с-1,
с-1,
![]() c-2.
(4)
c-2.
(4)
Знаки указывают,
что в момент
![]() с направление
с направление
![]() совпадает с направлением положительного
отсчета угла
совпадает с направлением положительного
отсчета угла
![]() ,
а направление
,
а направление
![]() ему противоположно; отметим это на рис.
К2б соответствующими дуговыми стрелками,
ему противоположно; отметим это на рис.
К2б соответствующими дуговыми стрелками,
![]() - направлен вниз по оси
- направлен вниз по оси
![]() ,
а
,
а
![]() - вверх.
- вверх.
Из рисунка находим
расстояние
![]() точки В1
от оси вращения
точки В1
от оси вращения
![]()
![]() см. Тогда в момент
см. Тогда в момент
![]() с, учитывая равенства (4), получим
с, учитывая равенства (4), получим
![]() см/c,
см/c,
![]() см/с2,
см/с2,
![]() см/с2.
(5)
см/с2.
(5)
Изобразим на рис.
К2б векторы
![]() и
и
![]() (с
учетом знаков
(с
учетом знаков
![]() и
и
![]() )
и
)
и
![]() направлены векторы
направлены векторы
![]() и
и
![]() перпендикулярно плоскости АDE,
а вектор
перпендикулярно плоскости АDE,
а вектор
![]() по линии В1С
к оси вращения.
по линии В1С
к оси вращения.
-
К о р и о л и с о в о у с к о р е н и е. Так как угол между вектором
 и осью вращения (вектором
и осью вращения (вектором
 )
равен 300,
то численно в момент времени
)
равен 300,
то численно в момент времени
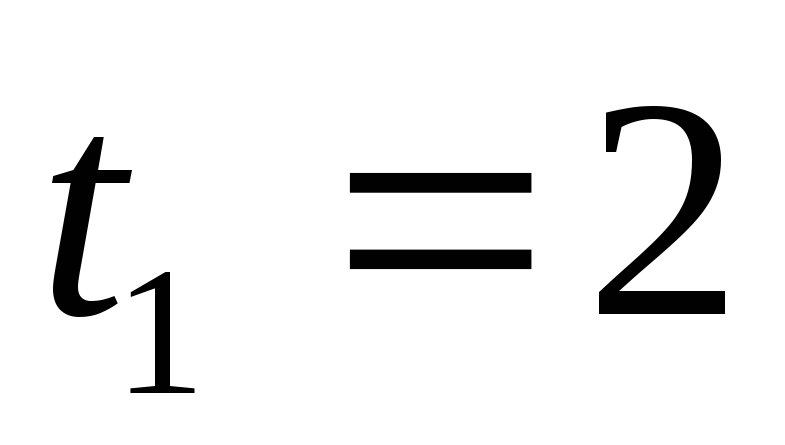 с
с
![]() см/c2.
(6)
см/c2.
(6)
Направление
![]() найдем по правилу Н.Е.Жуковского. Для
этого вектор
найдем по правилу Н.Е.Жуковского. Для
этого вектор
![]() спроектируем на плоскость, перпендикулярную
оси вращения (проекция направлена
противоположно вектору
спроектируем на плоскость, перпендикулярную
оси вращения (проекция направлена
противоположно вектору
![]() )
и затем эту проекцию повернем на 900
в сторону
)
и затем эту проекцию повернем на 900
в сторону
![]() ,
т. е. по ходу часовой стрелки; получим
направление вектора
,
т. е. по ходу часовой стрелки; получим
направление вектора
![]() .
Он направлен перпендикулярно плоскости
пластины так же, как вектор
.
Он направлен перпендикулярно плоскости
пластины так же, как вектор
![]() (см. рис. К2б).
(см. рис. К2б).
-
О п р е д е л е н и е
 .
Так как
.
Так как
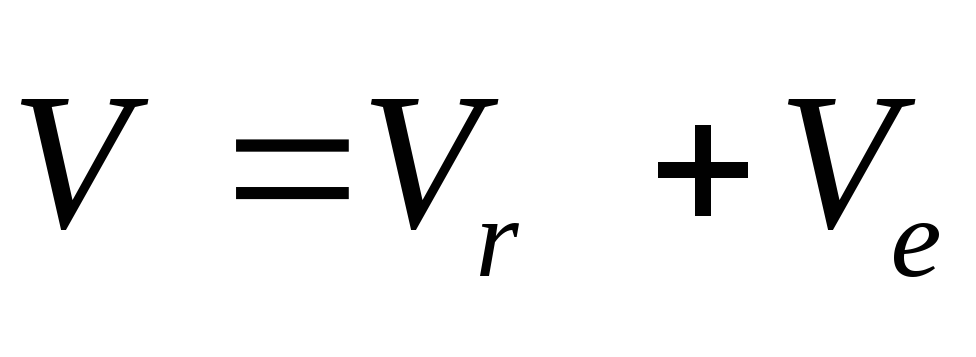 ,
а векторы
,
а векторы
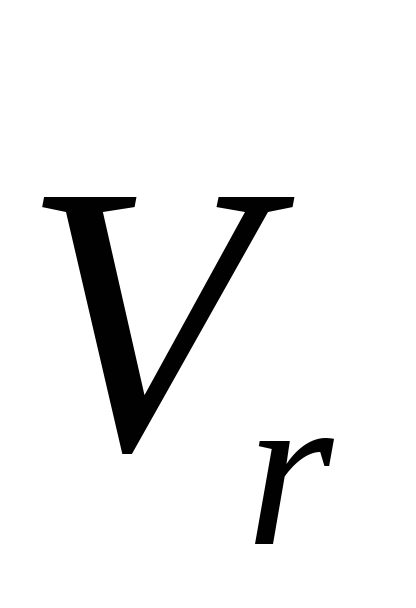 и
и
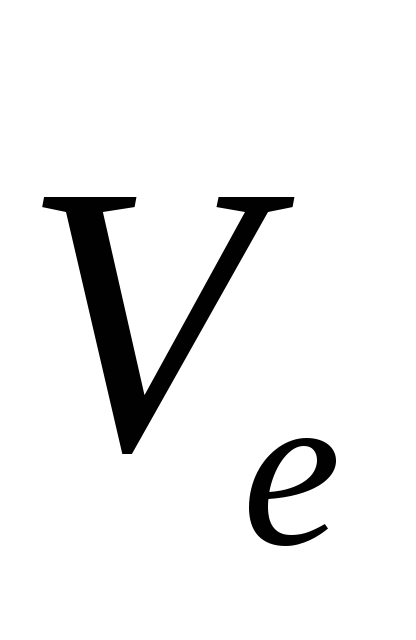 взаимно перпендикулярны, то
взаимно перпендикулярны, то
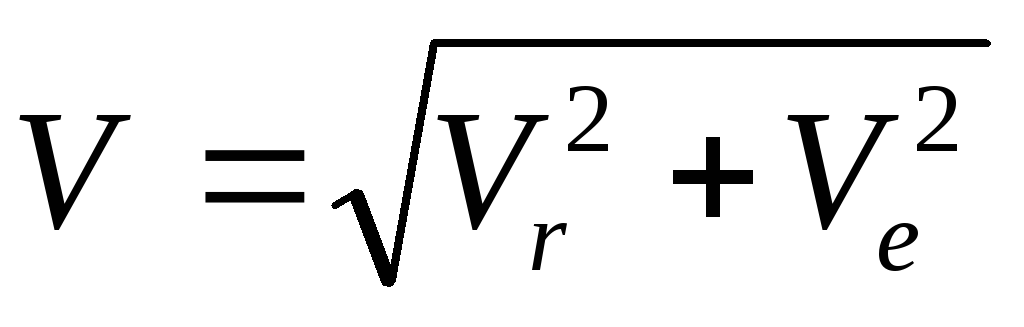 ;
в момент времени
;
в момент времени
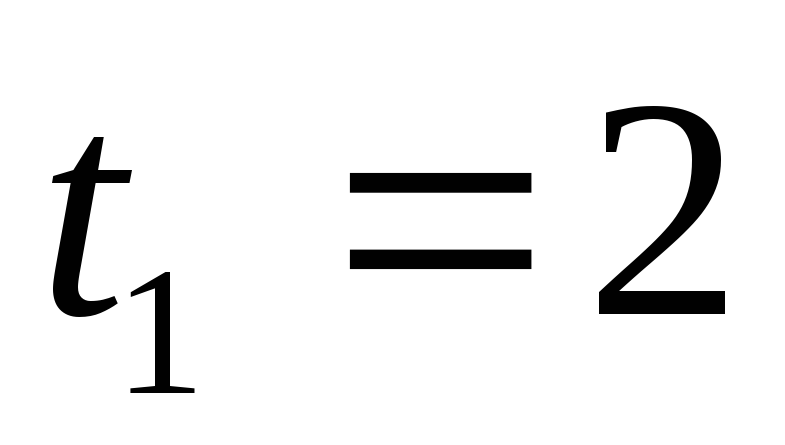 с
с
 см/c.
см/c. -
О п р е д е л е н и е
 .
По теореме о сложений ускорений
.
По теореме о сложений ускорений
![]() (7)
(7)
Для определения
![]() проведем координатные оси В1
проведем координатные оси В1![]() и вычислим проекции
и вычислим проекции
![]() на эти оси. Проектируя обе части равенства
(7) на оси В1
на эти оси. Проектируя обе части равенства
(7) на оси В1![]() и учтя одновременно равенства (3), (5),
(6), получим для момента времени
и учтя одновременно равенства (3), (5),
(6), получим для момента времени
![]() с:
с:

 2.0
2.0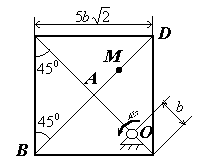 2.1
2.1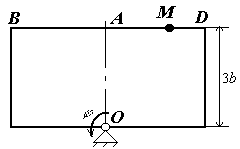
 2.3
2.3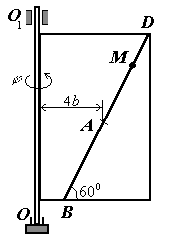 2.4
2.4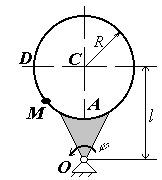 2.5
2.5
 2.7
2.7
 2.9
2.9