16. Порівняння нескінченно малих функцій. Таблиця еквівалентних

α(x) і β(x) при →- н.м.ф.

Означення:

1. Якщо =0, то α(x) називають н.м.ф.більш високого порядку малості, ніж β(x), і позначають α(x) =0 (β(x)) при .

2. Якщо , то кажуть, що α(x) і β(x)одного порядку малості при .

3. Якщо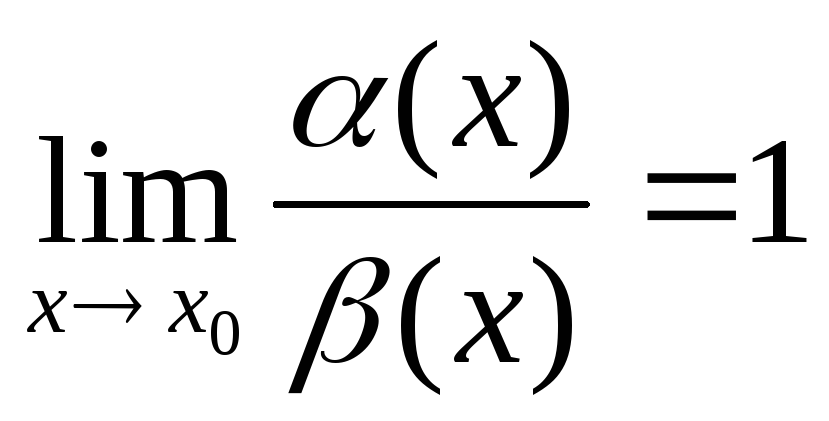, то α(x) і β(x)еквівалентні при , й позначають α(x) ~ β(x) при. Найчастіше за β(x) беруть(m>0).

4. Якщо , то кажуть, що α(x) - н.м.ф.m-того порядку малості, а x -головна частина н.м.ф. α(x).

Теорема. Якщо ~,~при, то.

Доведення

.

Таблиця еквівалентних

При справедливі такі еквівалентності :

Перші дві еквівалентні випливають із першої важливої границі. Третя і четверта доводяться за допомогою методу підстановки.

Доведення інших

5. За визначенням

;

6. ;

7. ~

.

Приклади:

1. , отже, при x→0, тобто– головна частина виразу 1-cos x при x→0.

2. Оскільки ~при x→0 , то головна частина виразупри x→0 є, абопри x→0.

17. Розкриття невизначеностей

Якщо й ми визначаємо, то кажуть, що виразпредставляє невизначеністьпри. Існує сім типів невизначеностей:. Наприклад, перша важлива границя розкриває невизначеність, а друга -.Оскількиа, то умовно можна записати, що

Прологарифмуємо останні три типи невизначеностей:

Це говорить про те, що шляхом елементарних перетворень один тип невизначеності можна звести в інший. Результат же розкриття невизначеності цілком залежить від закону зміни аргументу. Але все-таки є ряд загальних положень. Наприклад, при розкритті невизначеності бажано в чисельнику й знаменнику винести за дужки старший ступінь і скоротити; при розкритті невизначеностібажано чисельник і знаменник розкласти на множники; при розкритті невизначеності– використовувати другу важливу границю.

Лекція 5

18. Неперервність функції

Означення. Функція називається неперервною в точці х₀, якщо .

Функція називається неперервною праворуч (ліворуч), якщо ().

Для неперервної в точці х₀ функції .

x = х₀ + ∆x, тоді .

Тобто в δ(х₀) - околі малому приросту аргументу відповідає малий приріст функції.

Із властивостей границь випливають такі властивості неперервних функцій:

якщо неперервні в точці х₀ функції f(x) і φ(x), то

f(x)+ φ(x) , f(x)∙φ(x), с ∙ f(x)– неперервні в точці х₀ , а дріб − неперервний у точці х₀ , якщо φ(x₀) ≠0.

Означення. Якщо функція неперервна у всіх точках відрізка [a;b], то кажуть, що вона неперервна на цьому відрізку й позначають f(x) є C[a;b] (C− множина неперервних функцій).

За визначенням границі :такий, що при.

З рисунка видно, що при тому самому ε чим крутіший графік, тим менше δ, таким чином, δ(ε; х₀).

Теорема. Суперпозицією двох неперервних функцій є функція неперервна.

Доведення

y = f(U) неперервна в т (∙ ) U₀ , неперервна в точці х₀ і, тоді

, таким чином, неперервна в точці х₀.

19. Точки розриву функції

Якщо функція неперервна в точці х₀ , то А⁺ = А^‾ = f(х₀).

Означення. Якщо рівність А⁺ = А^‾ = f(х₀) порушується, то в точці х₀ розрив.

1. Якщо А⁺ = А^‾ ≠ f(х₀) і А⁺ , А^‾ − скінченні, то в точці х₀ розрив називається усувним.

2. Якщо А⁺≠А^‾ і обидві скінченні, то в точці х₀ розрив називається неусувним 1-ого роду.

3. Якщо хоча б одна з меж А⁺ , А^- дорівнює нескінченності або не існує, то в точці х₀ розрив називається неусувним 2-ого роду.

Приклад

У точці неусувний розрив 2-го роду.

У точці усувний розрив, тобто якщо, то нова функція в точці х=0 буде неперервною.

Означення. Функція називається кусково-неперервною на, якщо навона неперервна, крім нескінченного числа точок усувного розриву або неусувного розриву 1-го роду, причомуі- скінченні.

20. Неперервність деяких функцій

Елементарні функції типу: (),, всі тригонометричні, обернені тригонометричні неперервні на своїх ОДЗ.

Наприклад: ,

ОДЗ

, якщо , тобто, що збігається з ОДЗ.

21. Властивості функцій, неперервних на відрізку

, тоді

1. δ(х₀), у якій f(x) зберігає знак f(х₀)

(f(x) ∙ f(х₀) > 0),

2. хоча б одна (∙) ξ 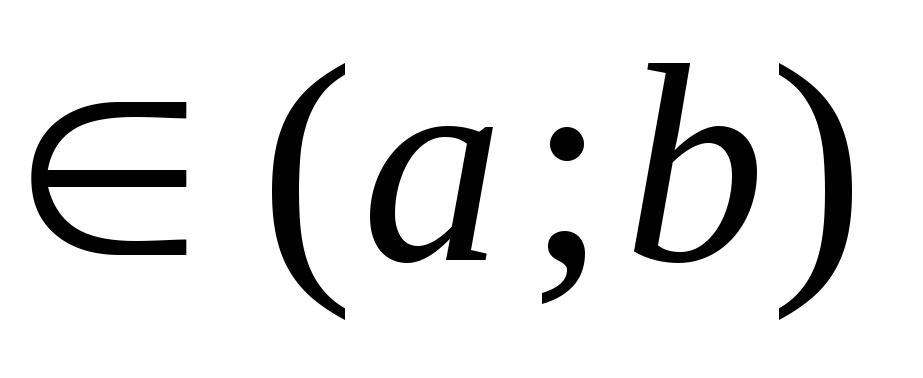, щоf(x) набуває проміжного значення між f(a) і f(b) (наприклад, якщо f(a) ∙ f(b) < 0, то f(ξ) = 0),

3. f(x) обмежена своїми найменшим і найбільшим значеннями ().

Лекція 6

22. Поняття оберненої функції

, аргумент , значення функціїй між множинамиX, Y взаємно однозначна відповідність.

Якщо ж y вважати аргументом, а x ­­­− значенням функції, то одержимо нову функцію, задану в неявному вигляді. Іноді x можна виразити через y, тобто

Означення. Функція ,,називаєтьсяоберненою функцією відносно ,,.

Приклад: ,,і,,взаємно обернені функції.

Зауваження

1. Графіки прямої й оберненої функцій симетричні відносно прямої .

2. Обернені тригонометричні функції й т.д. є оберненими не дляй т.д., а тільки для їхніх частин, що відповідають головним значенням аргументу x;

Наприклад: тільки при,має обернену функцію,,.