Лекція 1

Повторення з теорії множин

1. Множина натуральних чисел: .

2. Множина цілих чисел: .

3. Множина раціональних чисел:

.

4. Множина дійсних чисел:(усі раціональні й ірраціональні числа).

5. Множина комплексних чисел

.

Зауваження

1. Усі раціональні й ірраціональні числа геометрично зображуються точкою на числовій осі.

2. Усі раціональні числа подаються кінцевим або нескінченним періодичним десятковим дробом.

3. Усі ірраціональні числа подаються нескінченним неперіодичним десятковим дробом.

( )

Введемо позначення:

- нехай, - кожний, усякий, будь-який,- існує,- точка.

Означення: Абсолютна величина дійсного числа :

.

Зауваження:

1. .

2. .

1. Верхня й нижня межі множини дійсних чисел

Нехай нескінченна множина дійсних чисел, тобто.

Означення. Якщо задовольняє нерівність, тоназивають верхньою межею множини , а саму множинуобмеженою зверху.

Аналогічно визначається –нижня межа множини .

Якщо множина обмежена зверху й знизу, то її називають обмеженою.

Означення. Найменше з усіх називають, (supremum – точна верхня межа множини). Найбільше з усіх–(infimum – точна нижня межа множини).

Можна довести теорему: якщо не порожні множини дійсних чисел обмежені зверху (знизу), то вони мають точну верхню (нижню) грань ([4] c.45)

Зауваження: З визначення супремуму випливає:

1. ;

2. для хоча б один елементтакий, що

Аналогічно для інфімуму:

1. ;

2. для хоча б один елементтакий , що.

Якщо множина не обмежена зверху (знизу), то вважають, що, ().

2. Числова послідовність і її границя

Означення. Множина занумерованих дійсних чисел, розміщених у порядку зростання номерів, називається числовою послідовністю.

Приклади: .

Означення. Послідовність називається обмеженою, якщо обмежено множину її значень.

Означення. Якщо для будь-якого як завгодно малого числа знайдеться номертакий, що при,, то кажуть, щоа границя послідовності, і записують .

Зауваження:

1. .

Кажуть, що (належить-околу числа).

2. Якщо , то яким би малим не було число, в- околі числабуде нескінченна множина значень.

Означення:

Якщо будь-якому великому числу знайдеться номертакий, що при, то кажуть, що.У цьому випадку послідовність називаютьнескінченно великою (н.в.п.), якщо ж , то послідовність називаютьнескінченно малою (н.м.п.)

Приклади:

;

Якщо ,–cкінченне число, то послідовність називається збіжною, в інших випадках – розбіжною.

Приклади:збігається до числа 2.

, але обмежена й–розбігається.

Теорема (про єдину границю числової послідовності).

Якщо границя числової послідовності існує, то вона єдина.

Доведенняметодом «від супротивного»:

, наприклад, . За визначенням границітакі, що при

а , тоді

, або

суперечність, тоді .

Лема. Якщо ,то починаючи з деякого номера послідовністьобмежена.

Доведення

Візьмемо , визначимо номертакий, що при:

Тоді , тобто починаючи зпослідовністьобмежена числом.

Лекція 2

3. Нескінченно великі й нескінченно малі послідовності

Теорема (про зв'язок нескінченно великих (н. в. п.) і нескінченно малих послідовностей (н. м. п.)) .– н. в. п. при–н .м. п. при.

Доведення:

a) Дано: – н. в. п.аботакий, що при. Звідси, тобто.

b)Дано: – н. м. п., аботакий, що при. Звідси.

Уведемо символічний запис .

Теорема (про подання збіжної послідовності через границю і н. м. п.) , де– н. м. п. при.

Доведення:

Позначимо

a)Дано: , що при, тобто– н. м. п. при.

b)Дано: , що при, тобто.

Теорема:(про добуток н. м. п. на обмежену послідовність).

Добуток н. м. п. при на обмежену послідовність є н. м. п. при.

Доведення

і при. , що при

.

4. Основні теореми про границі послідовностей

тоді:

1.Т:

2.Т:

3.Т:

4.Т:

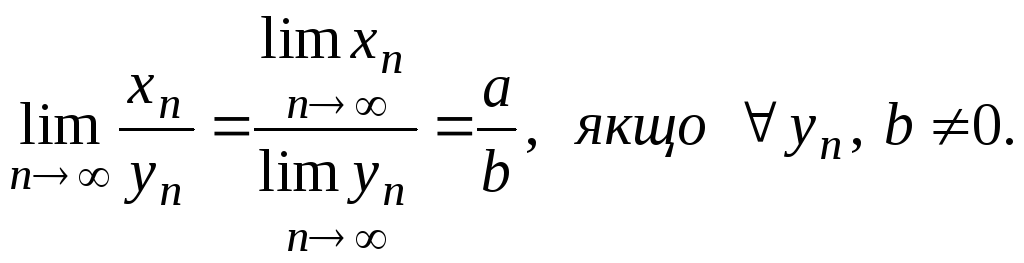
Доведення Т4(інші довести самостійно).

за теоремою про подання збіжної послідовності через н. м. п.

; - обмежена послідовність (див. лему),- н. м. п. приЗа теоремою про добуток н. м. п. на обмежену- н. м. п. при, тоді

5. Граничний перехід у нерівностях

Теорема (про граничний перехід у нерівностях).

і при

Доведення(від супротивного)

: (за основними теоремами про границі), що при, тоді

або

, – суперечність, отже.

Зауваження. Якщо при тодоведення аналогічне.

Теорема (про границю проміжної послідовності).

При й

Доведення

Зробимо граничний перехід у нерівності:

6 Монотонні послідовності

Означення. Послідовність називають монотонно зростаючою, якщо для, і монотонно спадною, якщо для.

Теорема Вейєрштраса. Якщо послідовність монотонно зростає (спадає) і обмежена зверху (знизу), то вона має скінченну границю.

Доведення

Нехай послідовність монотонно зростає й обмежена зверху йІз зауваження до точної верхньої границі дляхоча б один, щоабо

Оскільки послідовність монотонно зростає, то й, для всіх цих номерівАналогічно доводиться друга частина теореми.

Приклад. Довести, що

Розглянемо послідовність .

Оскільки при досить великих , тоді, тобто послідовність монотонно спадає й обмежена знизу нулем. За теоремою Вейєрштраса ця послідовність має скінченну границю А.

Таким чином,, що й було потрібно довести.

7. Число e

Розглянемо послідовність

За допомогою методу математичної індукції, використовуючи біном Ньютона, можна довести, що послідовність монотонно зростає й обмежена числом 3. Тоді за теоремою Вейєрштраса існує скінченна границя, яку позначимо буквою

- ірраціональне число.

Логарифми з основою e називають натуральними й позначають

Приклади

2. 

2. за теоремою про добуток н. м. п. на обмежену.

При розв’язуванні прикладів 1, 2 використовувались теореми:

Теорема 1. Послідовність- н.м. при тоді і тільки тоді, коли.

Теорема 2. Якщо ,і, тоді.

Теорема 3. Якщо ,,і, тоді.

Доведення даних теорем наведені в пункті 181.

Лекція 3

8. Функції

Означення. Якщо  за певним правилом ставиться у відповідність, то кажуть, що на множиніХ задана функція у = f(х), або задане відображення множини Х на множину Y.

Х- область визначення функції.

Y - область значень функції.

У математичному аналізі, якщо заздалегідь не зазначено, розглядають взаємно однозначну відповідність множин Х і Y, тобто  ставиться у відповідність тільки один елемент множини У і навпаки.

Правило f може бути задано формулою (аналітичне завдання функції), таблицею, графіком, алгоритмом.

Зауваження. Будь-яка послідовність є функцією цілочислового аргументу: .

Приклади.Крім функцій, які розглядаються в шкільному курсі, ми будемо ще розглядати такі функції:

1. Ціла раціональна функція, або многочлен (поліном), 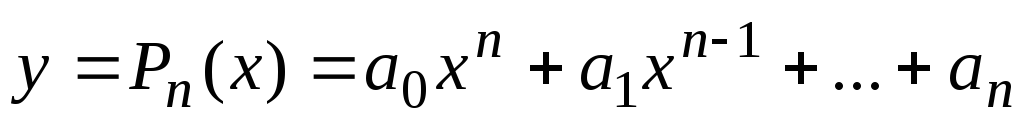, де числа.

2. Дробово-раціональна функція

.

3.

4. Ціла частина числа у = [х]

5

. Функція Діріхле

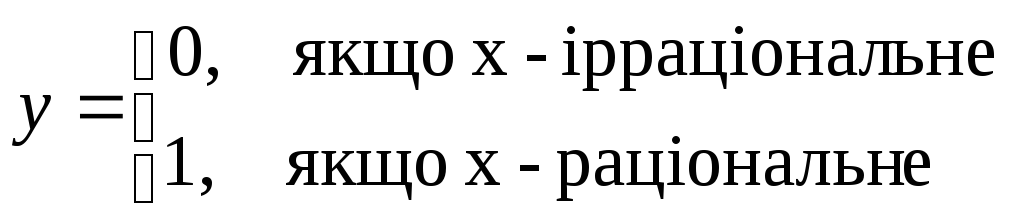
та інші функції.

Означення

1. Функція називається обмеженою зверху (знизу), якщо множина її значень У обмежена зверху (знизу).

2. Найменша верхня границя – , а найбільша нижня границя –.

3. Функція у = f(х) називається монотонно зростаючою (спадною), якщо при х₁ ≤ х₂ f(x₁) ≤ f(x₂) (f(x₁) ≥ f(x₂)).

9. Гіперболічні функції

Гіперболічний синус , гіперболічний косинус, гіперболічний тангенс і котангенс

З

ауважимо, що

10. Границя функції

Означення (за Коші)

Якщо  ε >0  δ=δ (ε)>0 таке, що при 0< |x-x₀|< δ |f(x) – a|< ε, то кажуть, що .

Зауваження

Якщо ,то приε(α), тобто яким би маленьким не було число ε, в ε – околі точки а буде незліченна множина значень функції.

Означення (за Гейне). Якщо для  послідовності X, що збігається до(), то а називається границею функції f(x) при.

Можна довести, що визначення за Коші й за Гейне еквівалентні, тобто з одного випливає інше.

Аналогічно можна дати визначення за Коші й за Гейне у випадку, якщо або.

(Зробити самостійно).

11. Теореми про границі функції

Оскільки визначення границі функції за Коші й за Гейне еквівалентні, то всі теореми, розглянуті для послідовностей, справедливі й для функцій.

Наприклад, теорема про вираження функції через межу й н.м.ф. : якщо ,то, де(x) н.м.ф. приі навпаки.

Або теорема про границю проміжної функції: якщо при і, то.

12. Односторонні границі

Означення. називається правосторонньою границею;називається лівосторонньою границею.

Приклади:

1)

(використовувався символічний запис);

2) .

Теорема.

Доведення:

а)

Для  ε >0  (ε) > 0 така, що приε .

Для  ε >0 (ε) > 0 така, що приε.

δ= найм ,

отже: ;

б)  ε >0  δ=δ(ε)>0 такий, що при ε .

Візьмемо , тоді приε, тобто.

Аналогічно для

13. Суперпозиція функцій і її границя

Означення. функціїy = f(u), , , функціяu = φ(x), ,. Тодіy = f(φ(x)), де ,називаєтьсясуперпозицією функцій, або складеною функцією, а u – проміжним аргументом.

Теорема. Якщо то.

Доведення

 ε >0  (ε)>0 така, що при< ε.

 така, що при ,.

Звідси  ε >0  (ε))=δ(ε)>0 така, що при< ε.

Таким чином.

Висновок.При обчисленні границі суперпозиції можна робити заміну змінних (або підстановку):

.

Лекція 4

14. Перша важлива границя

.

Доведення

,

,

- довжина дуги.

S_∆OAC^/ < Sсек < S_∆OA^/ _C^/

,

,

тому що в І і ІV чвертях cos x ≥ 0, при x≠0.

Оскільки , то за зауваженням до теореми про граничний перехід у нерівностях

.

15. Друга важлива границя

.

Доведення

і . Тодій, або.

За зауваженням до теореми про граничний перехід у нерівностях: при , тобто.

Зауваження:

1. , таким чином,;

2.;

3).