Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уманский государственный педагогический университет им. П. Тычины

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Квантова механіка_Модуль 4

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

743.73 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МОДУЛЬ IV. РЕЛЯТИВІСТСЬКА КВАНТОВА ТЕОРІЯ

Розділ VІІІ. Основні положення квантової теорії поля

§72. Теорія відносності і квантова механіка

Основи двох найвизначніших теорій 20 століття – СТВ і квантової механіки – були закладені майже одночасно. М.Планк ввів поняття про квант енергії у 1900 р., а перша робота А.Ейнштейна по СТВ була надрукована у 1905 р. Досить довго ці дві теорії розвивались паралельно і незалежно одна від одної, проте очевидною бу- ла необхідність їх об’єднання, і не тільки тому, що необхідно було розвинути метод квантового опису частинки з великими швидкостями.

По-перше, тому що квантова механіка, яка базувалась на рівняннях Шредінге- ра, описувала рух лише повільних мікрочастинок, і була непридатна для опису ква- нтових явищ з участю частинок, що рухаються зі швидкістю, близькою до швидко- сті світла. По-друге, процеси випромінювання і поглинання світла атомами вима- гають залучення релятивістських уявлень, оскільки фотони є суто релятивістськи- ми об’єктами.

Визначимо критерій, який встановлює область релятивістських явищ, із реля- тивістського співвідношення між енергією і імпульсом частинки:

E 2 = p2c2 + m2c4 ,

(1)

де m – маса спокою частинки. Релятивістською є область імпульсів, більших за комптонівський: p ≥ mc . При таких імпульсах кінетична енергія частинки стає бі- льшою за енергію спокою, так що закон збереження енергії не забороняє утворення нових частинок. Це приводить до незбереження числа взаємодіючих частинок, вна- слідок чого хвильова функція втрачає свій імовірнісний зміст і трактується як хви- льове поле.

Перехід від хвильової функції ψ нерелятивістської квантової механіки до хви- льового поля релятивістської квантової механіки пов'язаний з неможливістю лока- лізувати мікрочастинки в малих областях внаслідок співвідношення невизначенос-

тей Гейзенберга p ≥
тей Гейзенберга p ≥
2		x

. Дійсно, згідно з цією формулою, частинка, що локалізо-

вана в області х, має нижню межу для енергії

E = pc ~	c	,	(2)

	2 x

і якщо енергія достатньо велика (більша за енергію спокою), то можливе наро- дження нових частинок, поява пар частинка-античастинка. В такому випадку втра- чається зміст локалізації частинки у вказаній області, а разом з тим і звичайне імо- вірнісне трактування її функції стану. Граничний розмір області локалізації знай-

демо з умови (2) при E = mc2 :

mc2 =	2π c	x = λ	=	2π	=	h	.	(3)

	x	C		mc		mc

Величина λС відома під назвою комптонівської довжини хвилі частинки. Отже, го- ворити про локалізацію мікрочастинки в області з розмірами, меншими за компто- нівську довжину хвилі цієї частинки, немає змісту. Тому хвильова функція тепер ототожнюється з деяким хвильовим полем, що описує стан мікрочастинки через її параметри.

Релятивістська квантова теорія виявляється теорією хвильових полів, у яких

збудженими станами (квантами) є елементарні частинки. Це не є механіка однієї частинки в силовому полі або системи частинок, взаємодіючих через посередницт- во полів. Взаємодія полів приводить до народження або знищення частинок, фізич- ні параметри яких повинні визначатись в теорії по вигляду полів і закону їх взаємо- дії. Основна задача релятивістської теорії полягає в розрахунках ймовірностей пе- реходів в системі вільних до і після взаємодії мікрочастинок, тобто в розрахунках результату взаємодії.

§73. Рівняння Клейна-Гордона-Фока

Гамільтоніан вільної частинки в нерелятивістській теорії дорівнює:

H =

(1)

З цього співвідношення можна формально отримати рівняння Шредінгера, як-

∂

що замінити енергію Н оператором i

, а вектор p

оператором p = −i , і подія-

∂t

ти цими операторами на хвильову функцію ψ:

∂ψ

2 2

= −

ψ .

(2)

∂t

Для отримання таким же способом релятивістського рівняння необхідно ско-

ристатися релятивістським зв’язком між Е і p :

E 2 = p2c2 + m2 c4 −

2∂2ψ

= − 2c2 2ψ + m2c4ψ або

∂t 2

1 ∂2ψ

(3)

−

= −m

∂t

Цьому рівнянню можна придати релятивістськи інваріантну 4-вимірну форму.

Для цього введемо 4-вимірний оператор імпульсу pα (α = 0,1, 2, 3)з проекціями:

pα

= −i

∂

(4)

∂xα

Тоді рівняння (3) приймає вигляд:

(5)

pα

p ψ = −m

c ψ .

Можна також ввести лоренц-інваріантний оператор Даламбера - аналог 3-

вимірного оператора Лапласа ( =

∂2

∂x2

∂z2

∂y2

□=

∂2

−

(6)

c2 ∂t 2

так що рівняння (3) прийме вигляд:

2 □ψ = −m2 c2ψ .

(7)

Для релятивістської інваріантності рівнянь (3) або (5) необхідна також Лоренц-

інваріантність функції ψ (x, y, z,t ). Якщо ψ є скаляром перетворень Лоренца, то ми

отримаємо перше і найпростіше релятивістське квантове рівняння, запропоноване в 1926 р. і відоме під назвою рівняння Клейна-Гордона-Фока. Але рівняння Клейна- Гордона-Фока можна записувати і для тензора ψαβ ... будь-якого рангу.

Рівняння Шредінгера в нерелятивістській області універсальні в тому розумін- ні, що без врахування спіна його можна застосувати до будь-яких мікрочастинок.

Але важливий клас мікрочастинок з напівцілим спіном – ферміонів – цим рівнян- ням не охоплюється.

Рівняння Клейна-Гордона-Фока (3) може бути узагальнене на рух частинки в потенціальному полі, але ми обмежимось випадком вільного руху, який наочно проявляє якісні особливості опису мікрочастинок в релятивістській квантовій ме- ханіці.

Отримаємо рівняння неперервності для рівняння Клейна-Гордона-Фока. Для цього обидві частини рівняння (3) помножимо на ψ * і з отриманого рівняння від- німемо комплексно спряжене. Отримаємо рівність:

= 2

∂

−ψ

∂ ψ

(ψ ψ −ψ ψ ),

∂t

∂ 2

∂ψ

звідки

−ψ

= 2

(ψ ψ −ψ ψ )

∂t c

∂t

Права частина з точністю до сталого співмножника співпадає з виразом для гу- стини потоку ймовірності в шредінгерівській теорії. Вводячи недостаючий множ-

ник i , отримаємо: 2m

∂ i

∂ψ

)

(8)

−

−ψ

ψ −ψ ψ

∂t

∂t 2mc2

∂t

(

Оскільки вектор

j =

i
i	(ψ ψ −ψ ψ )	(9)
2m	(ψ ψ −ψ ψ )	(9)
2m

є густиною потоку ймовірності (9.5), то густина ймовірності виражається у випадку релятивістського рівняння (3) новою величиною:

w =	i		ψ	∂ψ	−ψ	∂ψ	(10)
		2
	2mc			∂t
						∂t

(в нерелятивістській теорії w = ψψ * ). З формули (10) видно, що ψ може приймати від’ємні значення. Це викликає труднощі в інтерпретації поняття про ймовірність місцезнаходження частинки в просторі без врахування яких-небудь інших її влас- тивостей, крім маси, яка входить в формулу. Але в рівнянні Клейна-Гордона-Фока закладені можливості виявлення додаткових властивостей частинки для зняття вка- заної проблеми.

§74. Частинки і античастинки в теорії Клейна-Гордона-Фока

Розв’язок рівняння Клейна-Гордона-Фока

1	∂2		m2c2		(1)
		− +		ψ = 0
c2		− +		ψ = 0
c2	∂t 2		2

будемо шукати у вигляді плоскої монохромної хвилі:

i (px−Et )	(2)
ψ = Ce

Підстановка цього розв’язку в (1) дає −

E 2

m2c2

= 0 ,

E 2 = p2c2 + m2c4

, звідки

2c2

E = ± p2 c2 + m2 c4

= ±c p2

+ m2 c2 = ±ε ,

(3)

1,2

де ε = c p2 + m2c2 .

Отже, плоскі хвилі є розв’язком рівняння для скалярних частинок при умові, що енергія, імпульс і маса останніх задовольняє формулі Ейнштейна (72.1)=(3), яка встановлює в СТВ зв'язок між енергією і імпульсом. Але в СТВ мова йшла про ма- кроскопічні тіла і розв’язокE2 < 0 відкидався як нефізичний. Зупинимось тепер на

знакові енергії частинки з заданою масою m і імпульсом p трохи детальніше. Згідно з формулою (3) неперервна множина позитивних значень енергії части-

нки масою m при всіх можливих значеннях імпульсу р обмежена знизу енергією спокою mc2 . Аналогічно від’ємні значення енергії обмежені зверху значенням - mc2 . Тим самим вся область допустимих енергій розірвана на дві частини забороненим

інтервалом шириною 2mc2 .

Макроскопічна фізика оперує з позитивними релятивістсь-

кими енергіями тіл, а оскільки скачкоподібних змін енергії, що

порушують її неперервний хід, тут не зустрічається, то і не розг-

+mc2

лядають від’ємні енергії.

В квантовій фізиці заборона на скачкоподібну зміну енергії

−mc2

знімається, але і тут від від’ємних енергій мікрочастинок прихо-

диться відмовлятись. Справа в тому, що «дна» у від’ємної області

Мал. 1

енергій немає, а це означає виділення нескінчених енергій при

необмеженому опусканні частинок вниз по енергетичним рівням.

Отже, енергія мікрочастинки з заданою масою і імпульсом зажди додатна і до-

рівнює ε

в формулі (3). Враховуючи цю обставину запишемо обидва розв’язки ре-

лятивістського рівняння (1) для вільних частинок:

= C e

(px−ε t );

= C

(px+ε t ) .

(4)

( +)

( −)

Вважається, що ці розв’язки відрізняються не енергією частинок; вона одна і та ж і дорівнює ε, але ці розв’язки описують 2 різних можливих стани частинки: ψ (+)

відповідає частинці, а ψ (−) - античастинці. Частинка і античастинка характеризу-

ються однією і тією ж масою, можуть мати (як у формулах (4)) однаковий імпульс, але відрізняються одна від одної знаком у функції стану, пов’язаним з такою внут- рішньою характеристикою, як електричний заряд.

Релятивістське рівняння Клейна-Гордона-Фока не тільки виявляє нову «сту- пінь вільності», яка проявляється як два можливих стани частинки. Обчислимо гус- тину ймовірності для частинки і античастинки за формулами:

w( + ) =

( + )

;

w( −) = −

ψ ( −)

(5)

mc2

Якщо тепер наділити частинки електричним зарядом е, то для густини заряду отримаємо:

= ew

eε

; ρ

= ew

= −

eε

2 .

(6)

( + )

mc2

( + )

( −)

mc2

( −)

Другими словами, існує 2 стани частинки, які відповідають двом зарядовим станам: ρ(+) > 0 i ρ(+) < 0 . Від’ємний знак в формулі для ρ(−) можна віднести до заряду. В

такому випадку частинка і античастинка відрізняються знаком заряду, який прий- має 2 значення: ±e . Тому розв’язки ψ (+) i ψ (+) для частинки і античастинки назива-

ють зарядово-спряженими. Труднощі трактування від’ємної густини ймовірності у формулі (61.10) тепер зникають. Мова йде, по суті, про густину заряду ρ = ±ew .

				99
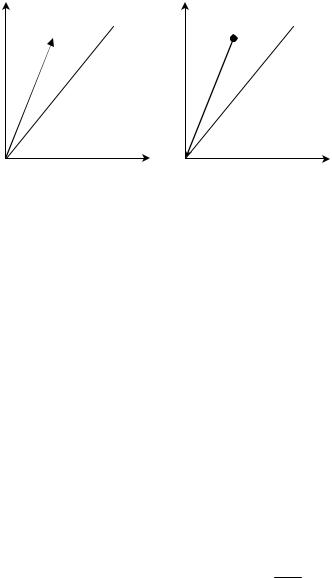
	х0=ct	х0=ct		Можна також пов’язати знак в
	х0=ct	х0=ct		функції стану частинки і античас-
				функції стану частинки і античас-
	A	A		тинки з геометричною інтерпрета-
				цією руху частинки в 4 – вимірному
				просторі. Для одновимірного випа-
				дку руху частинки і античастинки
				маємо діаграми (мал. 2). Знак (-) ві-
				днесемо до власного часу античас-
O	Мал. 2	O	х1=х	тинки, який йде в зворотному на-
	Мал. 2	х1=х	х1=х	прямку по відношенню до часу
				прямку по відношенню до часу
				спостерігача і власного часу части-

нки. Тому для одного і того ж імпульсу в системі спостерігача напрямки світової лінії у частинки і античастинки протилежні.

Введення античастинок вимагає розглядати тепер не окремі частинки, а хви- льове поле

	i	(px−ε t )			i	(px+ε t ) ,
ψ = C e		(px−ε t )	+ C	e		(px+ε t ) ,	(7)
1			2

збудженими станами (квантами) якого є частинки і античастинки. Хвильове поле релятивістської теорії в загальному випадку не несе інформації про місцезнахо- дження частинки в просторі, і лише в квазірелятивістському випадку старе тракту- вання ψ - функції як амплітуди ймовірності зберігається.

§75. Рівняння Дірака (НСО)

В попередніх параграфах було розглянуто релятивістськи інваріантне хвильове рівняння, яке справедливе для частинки з спіном 0. При цьому ми виявили, що ве- личина w , яку слід було б трактувати як густину ймовірності, приймає як додатні, так і від'ємні значення. Пов’язано це з тим, що рівняння Клейна-Гордона-Фока міс-

тить другу похідну від ψ по часу t ( ∂2ψ ). Отже, для усунення цього недоліку необ-

∂t 2

хідно, щоб розшукуване релятивістське узагальнення рівняння Шредінгера, яке б містило лише першу похідну по часу, як і саме рівняння Шредінгера. Проте, оскі- льки в усі релятивістськи інваріантні рівняння і вирази, просторові координати і час повинні входити однаковим чином, то в релятивістському узагальненні рівнян- ня Шредінгера повинні входити тільки перші похідні по координатам і часу.

Принцип суперпозиції вимагає, щоб релятивістське хвильове рівняння було лі- нійним. На основі цих міркувань для опису руху вільних частинок Дірак запропо- нував наступне рівняння:

i	∂ψ	=	β ′	∂	+ β ′	∂	+ β ′	∂	+ β	ψ .

	∂t		x	∂x	y	∂y	z	∂z		0

Якщо врахувати зв’язок між операторами проекцій імпульсів і похідними:

∂

, (p

= −i

, p y = −i

, p z

= −i

= −i ),

∂x

∂y

∂z

то рівняння (1) можна представити у вигляді:

∂ψ

= (β x

p x

+ β y

p y

+ β z

p z

β 0 )ψ .

∂t

(1)

(2)

Якщо ввести позначення

100

(3)

= β x

p x

β y

p y

β z

+ β 0

то рівняння (2) можна записати у формі

∂ψ

Hψ ,

(4)

∂t

яка має повну, хоч поки що формальну, схожість з рівнянням Шредінгера. Якщо

припустити, що оператор

дійсно є оператором Гамільтона, то між ним та опера-

тором імпульсу p

повинен існувати такий же зв’язок, як між енергією і імпульсом

в СТВ (72.1):

(5)

H = c

(p x

+ p y

+ pz

)+ m

Ця умова після підстановки в неї (3), піднесення до квадратів і

прирівнювання лі-

вої та правої частин (5), приводить до співвідношень для операторів β i :

2 2 2

;

= 0, i = x, y, z .

β x = β y = β z = c

; β

0 = m

β i β k +

β k β i

= 0 (i ≠ k ); β i β

0 + β 0 β i

Замість операторів

вводимо оператори αi ,

які відрізняються від них стали-

β i

ми множниками:

β .

β x

= cα x , β y = cα y ,

β z = cα z

, β 0 = mc

Для операторів α i β мають місце очевидні рівності:

α 2

= α 2

= β 2 = 1; α α

+ α

= 0, i ≠ k ; α

β + βα

= 0 .

(6)

i k

За допомогою введених операторів αi рівняння (2) матиме вигляд:

∂ψ

= c

(α x p x

+ α y p y

+ α z pz )+ mc2 β ψ .

(7)

∂t

Рівняння (9) - шукане узагальнення рівняння Шредінгера, яке називається рівнян- ням Дірака.


Якщо ввести векторний оператор рівністю α = i α x						+ jα y + kα z			, то рівняння Діра-
ка запишеться в ще більш компактному вигляді:
	∂ψ						2
							2	β .	(8)
i		= Hψ ;	H	= c α	p + mc
i	∂t	= Hψ ;	H	= c α	p + mc
	∂t
			Відмітимо перш за все, що дія цих опе-
Звернемось до операторів α x ,α y ,α z , β .			Відмітимо перш за все, що дія цих опе-

раторів не може звестись до множення хвильової функції ψ на деякі сталі числа. За допомогою операторів, які зводяться до сталих чисел, неможливо було б задоволь-

нити співвідношення (6). Тому оператори		шукають у вигляді квадрат-
	α x ,α y ,α z , β

них матриць. Безпосередньою перевіркою можна переконатись, що умовам (6) за- довольняють матриці 4 × 4 :

		0		0	0	1					0			0 0		−i

α		=	0	0	1	0 ;			α		=	0		0 i		0	;
	x		0	1	0	0				y		0		−i 0		0

			1	0	0	0					i			0 0		0	(9)
		0					0				1 0						(9)
		0		0 1			0				1 0				0	0

α		=	0	0 0 −1				;	β =				0 1		0	0	.
	z		1	0 0			0						0 0		−1	0

			0	−1 0			0						0 0		0	−1

Матриці (9) записати в більш скороченому вигляді, використовуючи матриці

										101
Паулі (23.4):
α x	0	σ x	;α y		0 σ y	0	σ z	I	0	(10)
α x	=		;α y	=	;α z	=		; β =	.	(10)
	σ x	0			σ y 0	σ z	0	0	−I
Прийнявши для					матричні вирази (9), ми повинні приписати хви-
Прийнявши для		α x ,α y ,α z , β			матричні вирази (9), ми повинні приписати хви-

льовій функції 4 компоненти. Лише в цьому випадку чотири рівняння, на які розпа- даються рівняння (7), при підстановці в нього чотирирядних матриць, містить 4 не- відомі функції. 4–компонентну функцію ψ записуються у вигляді матриці – стовп- чика:

ψ	1

ψ = ψ	2	.	(11)

ψ	3
	3

ψ	4

Її називають біспінором Дірака. В явному вигляді рівняння Дірака отримуються при використанні правил множення матриць:

		∂ψ1
i
i		∂t
		∂t
		∂ψ 2
i
i		∂t
		∂ψ 3
i		∂ψ 3
i
		∂t
		∂ψ 4
		∂ψ 4

i
		∂t

=c (p x − i p y )ψ 4 + c p zψ 3 + mc2ψ1

=c (p x + i p y )ψ 3 − c p zψ 4 + mc2ψ 2

(12)

=c (p x − i p y )ψ 2 + c p zψ1 + mc2ψ 3

=c (p x + i p y )ψ1 − c p zψ 2 + mc2ψ 4

Аналогічно рівнянню Клейна-Гордона-Фока, рівняння Дірака приводить до рі- вняння неперервності:

∂
∂	ψ +ψ = − div(cψ + αψ ) ,	(13)

∂t

де ψ + – матриця–стрічка, спряжена матриці–стовпчику:ψ + = (ψ1*ψ 2*ψ 3*ψ 4* )

Величина ψ +ψ суттєво додатна, тому немає перешкод розглядати її як густину ймовірності положення частинки в просторі. Але багатокомпонентність ψ -функції приводить до виразу для ψ +ψ у вигляді суми 4-х доданків:

ψ +ψ = ψ *ψ	1	+ψ *ψ	2	+ψ *ψ	3	+ψ *ψ	4	,	(14)
1	1	2	2	3	3	4	4

тому цій величині не можна дати прямого трактування ймовірності координат час-

тинки. Відповідно ψ слід розглядати як поле, кванти якого є частинки зі спіном 1 .

Отже, рівняння Дірака описують частинки зі спіном 1 , тобто ферміони.

§ 76. Частинки і античастинки в теорії Дірака (НСО)

Попробуємо в якості розв’язку рівняння Дірака вільної частинки

i	∂ψ	= (cα p + mc2 β )ψ	(1)
	∂t

плоску монохроматичну хвилю

де u – деяка незалежна від (r , t )

		− Et )
	i(pr
ψ = ue ,			(2)

одностовпчикова матриця. Така чотирикомпонент-

102

на функція ψ описує вільну частинку з масою m і імпульсом p . Підстановка функ- ції (2) в рівняння (1) дає рівність

Eu = (cα p + mc2 β )u.

(3)

Для знаходження u виразимо 4-рядкові матриці α і β через дворядкові матриці

Паулі σ і змінимо чотирирядковий стовпчик u на два дворядкових:

u =

′

В результаті отримаємо:

+ mc2

(4)

= cp

ω′

−1

ω′

Рівність (4), прочитана пострічно для 2-х рядкових матриць, приводить до сис-

теми рівнянь

(E − mc2 )

ω − cpσω ′ = 0

(5)

(E + mc2 )

ω ′ − cpσω− = 0

Відмінні від нуля розв’язки отримуються, якщо визначник системи обертається в нуль: E 2 − m2 c4 − c2 (pσ )2 = 0, звідки енергія частинки

E = ±ε , ε = c2 p2	+ m2c4 .	(6)
1,2

Врезультаті, як і в § 62, отримано розв’язки двох типів для вільних частинок:

i(pr − Et ) i(pr + Et )

ψ	( + )	= u e	, ψ	( − )	= u	e .	(7)
	( + )	1		( − )	2

Ці розв’язки інтерпретуються як два заряджено-спряжені стани – частинки і анти- частинки (електрона і позитрона). Можна показати, що u1 і u2 є базисними спіно-

вими функціями електрона і позитрона і мають вигляд:

										1						0							0												0
							1				0			1			1			1				0									1			0		(8)
						u1			=		0	,	u1 −			=	0	, u 2				=		1			,		u		2	−		=		0
						u1			=			,	u1 −			=		, u 2				=					,		u		2	−	2	=
							2							2						2													2

										0						0							0													1
Ці функції є власними функціями оператора спіна																							і оператора проекції спіна sɵz ,
Ці функції є власними функціями оператора спіна																						sɵ	і оператора проекції спіна sɵz ,
які в релятивістській теорії мають вигляд:
																													1				0	0			0
								σ				0				σ z		0													0 −1 0						0
						sɵ =							, sɵz =						= [		23.5] =																	(9)
						sɵ =							, sɵz =						= [		23.5] =																	(9)
								2 0			σ				2 0			σ z									2				0 0 1						0

																													0				0	0		−1
Функціям						(8) відповідають						власні				значення					оператора												sɵz ,		які			дорівнюють
	, −		,	, −		. Неважко також знайти модуль спіна:																s =						3		. Все це свідчить про те,
	, −		,	, −		. Неважко також знайти модуль спіна:																s =								. Все це свідчить про те,
2	2		2		2																					2
що рівняння Дірака описує частинки з напівцілим спіном (ферміони).
		Вільне хвильове поле, що відповідає електронам і позитронам, виражається лі-
нійною суперпозицією розв’язків (7), де спінові множники є матриці (8):

												ψ (r , t ) = A1u1e						i(pr − Et )							i(pr + Et )
												ψ (r , t ) = A1u1e								+ A2 u2 e																		(10)

Хвильова функція(10) несе інформацію про кванти поля – електрони і позит- рони, їх імпульси, енергії спіни.

103

§ 77. Рівняння Паулі

Розглянемо тепер, як перетвориться рівняння Дірака, якщо в ньому зробити перехід до нерелятивістського наближення. Дослідимо загальний випадок, коли ча- стинка рухається у зовнішньому електромагнітному полі. Виділимо перш за все у рівнянні Дірака енергію спокою, тобто проведемо перетворення виду

ψ =ψ ′e−imc2t / .

(1)

Врахування електромагнітного поля у квантовій механіці здійснюється шля-

хом заміни оператора імпульсу p

на

−

A з добавлянням до оператора Гаміль-

тона

і ϕ - векторний і скалярний потенціали поля. Це приво-

H доданку еϕ, де A

дить до рівняння Дірака

∂ψ

β ψ .

(2)

= c α

p −

A + eϕ + mc

∂t

Підставивши в (2) хвильову функцію (3), отримаємо рівняння

	∂ψ ′			e			2
i		= c α	p −		A	+ eϕ + mc		(β −1)	ψ ′ .
i		= c α	p −		A	+ eϕ + mc		(β −1)	ψ ′ .
	∂t			c

	ω	, то точно так же,
Якщо хвильову функцію записати у вигляді u =		, то точно так же,
	ω′

вільної частинки (§76), отримаємо рівняння для ω і ω':

	∂ω				e
							A ω′ + eϕω,
i		= c σ p		−
i		= c σ p		−
	∂t				c
	∂ω′					e
	∂ω′					e		2	ω′ + eϕω′.
i		= c σ	p −				A	ω − 2mc
i		= c σ	p −				A	ω − 2mc
	∂t					c
	∂t					c

(2')

як і для

(3)

Як завжди, граничний перехід до нерелятивістського наближення відповідає формальному розкладанню по степеням с. Припустимо спочатку, що ω' ~ω/c. Тоді в

другому з рівнянь (3) можна знехтувати членами i ∂ω′ і eω' як малими у порівнян-

∂t

ні з величинами

c σ

p −

ω та 2mc2ω′ ,

пропорційними с. Тоді отримуємо для

спінора ω' вираз

ω′ =

A ω ,

(4)

p −

2mc

що узгоджується з нашим припущенням. Підставляючи (4) у перше з рівнянь (3), знаходимо

	∂ω 1				e 2
			σ				ω + eϕω .	(5)
i		=		p −		A

	∂t	2m			c

Розкриємо квадрат оператора в явному вигляді:

e 2

Az .

p −

= σ x p x

−

+ σ y p y

−

+ σ z p z

−

При перемножуванні слід пам'ятати, що оператори p і A не комутують між собою. Виконуючи множення, знаходимо

104

p −

= σ x

p x

−

+ σ y

p y −

σ z

p z

−

(6)

+σ xσ y p x

−

Ax p y

−

+ σ yσ x p y

−

Ay p x −

+ σ xσ z p x −

Ax p z

−

+σ zσ x p z

−

Az p x

−

σ yσ z p y

−

Ay p z

−

Az +

σ zσ y p z

−

Az p y

−

Ay .

Враховуючи, що для матриць Паулі мають місце співвідношення σх2=σy2=σz2=1,

приведемо суму перших трьох доданків до вигляду:

σ x

p x

−

+ σ y

p y

−

+ σ z

p z

−

Подальші перетворення проводитимемо тільки з членами

(7)

σ xσ y p x

−

p y

−

+ σ yσ x p y

−

p x

−

оскільки решта доданків перетворюватимуться аналогічно. Так як матриці σх і σy антикомутують, вираз (7) можна переписати у вигляді:

ce σ xσ y (− p x Ay − Ax p y + p y Ax + Ay p x ).

Використовуючи властивості комутаторів операторів p

з операторами,

що залежать від координат, маємо

∂A

∂Ay

i e

∂Ay

∂A

i e

σ xσ y −i

+ i

σ xσ y

−

σ xσ y

rot z

A =

σ xσ y H z .

∂y

∂x

∂y

А оскільки σ σ =іσ , то остаточно знайдемо

i e

σ σ

= −

.Здійснюючи анало-

y z

x y

гічні перетворення з рештою доданків у (6), отримаємо

		e	2
σ	p −		A
σ	p −	c	A
		c

	e 2			e
= p −		A	−		σ H .	(8)

	c			c

Підставляючи (8) у (5), отримаємо так зване рівняння Паулі, яке є нерелятиві- стським наближенням рівняння Паулі:

	∂ω		1		e 2			e
i		=		p −		A	+ eϕ −		σ H ω .	(9)
i		=		p −		A	+ eϕ −		σ H ω .	(9)
	∂t		2m		c			2mc

З нього, зокрема, видно, що з теорії Дірака випливає не лише існування спіну час- тинок, рівного ћ/2 (§76), але й наявність у частинок власного магнітного моменту

µ =	e	.	(10)

	2mc

Тепер ми можемо уточнити питання про те, до яких частинок, що мають спін ћ/2, можна застосовувати рівняння Дірака. Якщо під m розуміти масу електрона, то виходить хороша узгодженість між обчисленим і виміряним значенням магнітного моменту. Таким чином, рівняння Дірака описує поведінку електронів з великим ступенем точності. Рівняння Дірака дозволяє також успішно описати властивості нейтрино - частинки з нульовою масою спокою m = 0 і півцілим спіном. Проте спроби застосувати рівняння Дірака до важких частинок з спіном 1/2 - протона і нейтрона - не привели до задовільних результатів. Причина цього – участь нуклонів у сильній взаємодії, через що роль електромагнітної взаємодії у поведінці цих час- тинок є менш суттєвою.

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.03.2015209.41 Кб40Зоопсихологыя Т.2.doc
#
01.07.202553.06 Кб0индз - копия.docx
#
07.02.2015593.24 Кб62Квантова механіка. Лекції. Модуль 1.pdf
#
07.02.20151.26 Mб27Квантова механіка_Модуль 2.pdf
#
07.02.2015658.8 Кб33Квантова механіка_Модуль 3.pdf
#
07.02.2015743.73 Кб20Квантова механіка_Модуль 4.pdf
#
20.03.2016903.26 Кб39Кенігсбергер Г. Середньовічна Європа 400 - 1500 рр..rtf
#
07.02.201516.41 Mб658Киреев Н. Г. - История Турции. XX век - 2007.pdf
#
07.09.201983.32 Кб19Кислотні опади.docx
#
21.08.2019451.07 Кб2ККЗ ФК.doc
#
16.11.2019292.35 Кб6ККР адм право.doc