1. Кг живой массы тела. За время опыта животные дали сле­дующие прибавки живой массы тела (табл. 35).

Таблица 35

Средние арифметические привесов: в опыте =. в контроле Разница Чтобы установить, достоверна или случайна эта раз­ница, нужно определить ошибку разности средних по форму­ле (74):

Отсюда По табл. V Приложений для 1%-ного уровня значимости и числа степеней свободы 6 = 9 + 8—2=15 находимТак какнулевая гипотеза опроверга­ется на высоком уровне значимости (Р<0,01). Разница между средними величинами опыта и контроля оказалась в высшей степени достоверной.

Пример 2. На двух группах лабораторных мышей — опыт­нойи контрольной— изучали воздействие на организм нового препарата. После месячных испытаний масса тела животных, выраженная в граммах, варьировала следую­щим образом:

Разница между среднимиДля определения ошибки этой разности предварительно рассчитаем девиаты:

и Отсюда ошибка разности средних выразится величиной

иКритерий Для k=9+11—2=18 и 5%-ного уровня значимости в табл. V Приложений находим Так какнулевая гипотеза остается в силе.

НеопровержениеHо-гипотезы нельзя рассматривать как до­казательство равенства между неизвестными параметрами сово­купностей, из которых извлечены сравниваемые , выборки. В таких случаях вопрос о преимуществе одной статистической совокупности перед другой остается открытым. Ведь не исклю­чено, что при повторных испытаниях H₀-гипотеза может ока­заться несостоятельной. Более того, и в тех случаях, когда Hо-гипотеза опровергается, не следует спешить с окончатель­ным выводом.

Следует заметить, что вышеизложенное применение t-крите­рия предполагает, что дисперсии сравниваемых групп одинако­вы: Если это не так, то величину критерия находят по формуле

а число степеней свободы — по следующим формулам:

а) при

б) при

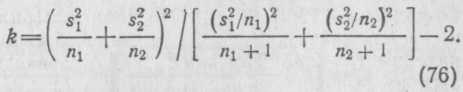
Так, при изучении влияния кобальта на массу тела кроли­ков (см. пример 1) дисперсии равныи(см. табл. 35). Видно, что

Следовательно, величину критерия необходимо определять с учетом неравенства дисперсий. Предварительно найдемиВеличина t-крите­рия равнаЗатем опре­деляем .и В результате Дляив табл. V Приложений находим

Так както H₀-гипотеза отвергается.

Правильное применение t-критерия предполагает нормаль­ное распределение совокупностей, из которых извлечены срав­ниваемые выборки, и равенство генеральных дисперсий. Если эти условия не выполняются, то t-критерий применять не сле­дует. В таких случаях более эффективными будут непарамет­рические критерии.

Оценка средней разности между выборками с попарно связанными вариантами. Сравниваемые выборки нередко представляют собой ряды попарно связанных вариант, т. е. являются зависимыми выборками.В таких слу­чаяхоценкой разности между генеральными средствамибудет средняя разность, определяемая из суммы раз­ностей между попарно связанными вариантами сравниваемых групп, т. е.

Оценкой генеральной дисперсииразности среднихбудет выборочная дисперсия

В формулах (77) и (78) п — число парных наблюдений;величинаидентична разности средних, т. е.

Ошибку средней разностиобозначаемую символом определяют по формулам

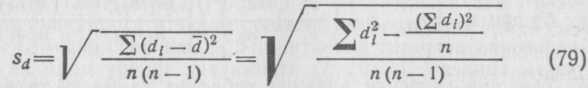
или

Если члены генеральной совокупности распределяются нор­мально, то и разности между нимибудут распределяться нор­мально и случайная величинабудет иметь распре­деление Стьюдента сстепенями свободы. Hо-гипотеза сводится к предположению, чтоОтсюда /-крите­рий выразится в виде отношения средней разности к своей ошибке, т. е.Еслидля принятого уровня зна­чимости и числа степеней свободы k = n—1, то нулевая гипоте­за должна быть отвергнута.

Пример 3. На протяжении ряда лет в условиях Одесской опытной станции изучали влияние черного и апрельского пара на урожай ржи. Результаты опыта учитывали по массе 1000 зерен (табл. 36).

Таблица Зв

В табл. 36 приведены выборки с попарно связанными вари­антами: несомненно, что каждый год имел свои специфические условия, которые одинаково влияли на урожай ржи, посеян­ной как по черному, так и по апрельскому пару. Поэтому обра­батывать полученные данные нужно с учетом тех условий, в которых проводили эксперимент. Из табл. 36 видно, что уро­жай ржи по апрельскому пару несколько выше, чем по черно­му. Средняя разностьОпределяем ошибку этой разности:

КритерийДляи (см. табл. V Приложений). Так както Н₀-гипотезу отвергают на высоком уровне значимости Следовательно, с вероятностьюможно утверждать, что

разница между сравниваемыми выборками статистически дос­товерна.

Пример 4. В результате семилетних исследований урожай­ности ячменя и овса в условиях нечерноземной зоны РСФСР были получены следующие данные (табл. 37).

Таблица 37

Разница между средним урожаем ячменя и овса составила 8,54—7,56 = 0,98 ц/га. Ошибка этой разницы=ОтсюдаЭта величина не превышает критический уровеньдля 5%-ного уровня

значимости и числа степеней свободы k= (7—1)=6. Следова­тельно, нулевую гипотезу здесь отбросить нельзя.

Оценку средней разности можно произвести по доверитель­номуинтервалу, построенному на основании полученной разно­стии ее ошибкиЕсли нижняя граница доверительного интервала окажется с положительным знаком, это будет сви­детельствовать о достоверности разницы. Если же нижняя гра­ница доверительного интервала будет с отрицательным зна­ком, это будет служить указанием на случайный характер наблюдаемой средней разности.

Так, в примереНижняя

граница 95%-ного доверительного интервала (0,52—0,24 = 0,28) оказалась с положительным знаком, тогда как в примере 4 и нижняя граница довери­тельного интервала (0,98—1,04= —0,06) оказалась с отрица­тельным знаком, что не дает основания для отклонения нуле­вой гипотезы.

Оценка разности между долями. Выборочная доля зависит от числа единиц в выборке, имеющих учитывае­мый признак, а общее число таких единиц в генеральной сово­купности определяет генеральнуюдолюОценкой разности между генеральными долямислужит разность между выборочными долямиОтношение этой разностик своей ошибке дает случайную величину котораяследует t-распределению Стьюдента. H₀-гипотезу, или предпо­ложение о том, чтоотвергают, еслидля k = п₁ + п₂—2 и принятого уровня значимостиОшибка разности между долями, взятыми из приблизительно равновеликих выбо­рок (когда численности групп различаются не более чем на 25%), вычисляют по формуле

гдеЕсли доли выражены в процентах от общего числа наблюдений, ошибку разности между ними определяют по формуле

Сопоставляемые группы п₁и п₂ могут быть выражены абсо­лютными числами т₁и m₂. Ошибка наблюдаемой между ними разности определяется по следующей формуле:

но так както формулу (81) можно представить и в таком виде:

Когда сравнивают доли из неравновеликих выборок и приошибку разности между ними определяют по формуле

р определяют как средневзвешенную из и долей, или же из абсолютных численностей групп:

В этих формулах n₁ и n₂ — численности групп, на которых определяют долии Если доли выражают в процентах от п, то вместо нужно брать

Если же неравновеликие группы выражены абсолютными чис­ламииошибку разности между ними определяют по формуле

Тема № 7.Регрессионный анализ.

Цель– познакомиться с регрессионным анализом.

Краткое содержание.

График корреляционной зависимости по уравнению функции ỹ_x=f(x) или ẍ_y,=f(у). Условные средние. Регрессия как изменение функции в зависимости от измене­ний одного или нескольких аргументов. Уравнения регрессии, эмпирические и теоретически вы­численные ряды регрессии, их графики, линии регрессии, коэффициенты линейной и нелинейной рег­рессии. За­дача регрессионного анализа - предвидеть возможные из­менения одного признака Y на основании известных изменений другого X, связанного с первым корреляционно. Основная характеристика коэффициента регрессии. Расчет коэффициентов регрессии, составление уравнений регрессии. Работа в среде Ехсеl. Расчет коэффициентов регрессии, составление уравнений регрессии с помощью средств электронных таблиц и функций Ехсеl, а также при использовании пакета «Анализ данных».

Тема № 8.Дисперсионный анализ.

Цель– познакомиться с дисперсионным анализом.

Краткое содержание. Результативны­е признаки. Факторы как причины изменения величины результативного признака. Регулируемые или организованные факторы и нерегулируемые. Градации регулируемого фактора. Дисперсионный анализ - разложение общей изменчивости признака на составные части: вариацию, определяемую действием изучаемого конкретного фактора, и вариацию, вызываемую случайными факторами. Дисперсионный однофакторный комплекс - действие на признак одного регулируемо­го фактора. Дисперсионные комплексы равномерные, пропорциональные (ортогональные) и неравномерные (неортогональные). Группировка совокупности по признаку-фактору. Выявление степени влияния признака-фактора на признак-результат по расчету нескольких видов дисперсий: общей, межгрупповой и внутригрупповой. Правило сложения дисперсий. Отношение межгрупповой дисперсии (факториальной дисперсии) к внутригрупповой, или остаточной, дисперсии - критерий оценки влияния, регулируемых в опыте факторов на результативный признак. Двух-, трех-и многофакторный анализ - действие на признак двух, трех или большего числа регулируемых факторов. Общие схемы дисперсионного анализа двухфакторных орто­гональных комплексов. Анализ двухфакторных комплексов - действие каждого фактора в отдельности и их совместное действие на результативный признак. Неортогональные комплексы. Работа в среде Ехсеl. Анализ однофакторных и двухфакторных комплексов - действие каждого фактора в отдельности и их совместное действие на результативный признак с помощью средств электронных таблиц и функций Ехсеl, а также при использовании пакета «Анализ данных». Расчет силы влияния факторов.

Тема № 9.Вопросы планирования исследования

Цель– изучить вопросы планирования исследования.

Задачи. Приближенные оценки основных статистических показателей. Определение необходимого объема выборки.

Краткое содержание. Классические работы Р. Фишера открыли новую страницу в истории биометрии: они показали, что планирование эксперимен­тов и обработка их результатов — это две тесно связанные меж­ду собой задачи статистического анализа. Это открытие легло в основу разработки теории планирования экспериментов, которая в настоящее время находит применение не только при проведе­нии сельскохозяйственных опытов, на базе которых она возникла, но и в различных областях биологии, медицины, антропологии, в сфере других научно-практических дисциплин, включая и со­циально-экономические исследования.

Планирование экспериментов, как уже отмечалось в пре­дисловии к этой книге, стало самостоятельным разделом био­метрии, которому посвящена огромная литература. В началь­ном курсе биометрии невозможно осветить все аспекты теории экспериментов. Здесь будут рассмотрены лишь некоторые об­щие положения, относящиеся к этой сложной и многогранной проблеме.

Термин «эксперимент» (от лат. experimentum — опыт) означа­ет искусственно организуемый комплекс условий, в которых ис­пытывают воздействие того или иного фактора или одновременно нескольких факторов на результативный признак. В земледелии это полевые опыты; в животноводстве — опыты по кормлению жи­вотных, по уходу за ними; в педагогике — опыты по проверке но­вых методов обучения и воспитания учащихся; в фармакологии — испытание эффективности новых лечебных препаратов; в меди­цине— проверка разных способов лечения больных и т. д.

Исследовательская работа не только сводится к эксперимен­там; ее проводят и вне их на основе непосредственных наблю­дений. Так что выражение «планирование исследований» ока­зывается более емким, а следовательно, и более подходящим, чем введенный Р. Фишером (1930) термин «планирование экспери­ментов». Конечно, и термин «эксперимент» можно применять в более широком смысле, понимая под ним любые испытания, про­водимые исследователем в отношении изучаемого объекта. При всем разнообразии методов исследовательской работы задача планирования сводится к тому, чтобы при возможно минималь­ных объемах наблюдений получать достаточно полную инфор­мацию об изучаемых объектах.

С варьированием результатов наблюдений связана повторность вариантов опыта, позволяющая повысить точность оценок гене­ральных параметров, надежность выводов, которые делает иссле­дователь на основании выборочных.показателей. Под повторнос­тью в полевом опыте понимают число одноименных делянок для каждого варианта опыта. В лабораторных условиях повторность может выражаться числом одинаковых проб серий одновремен­ных испытаний, измерений и т. п. повторений одного и того же варианта опыта. Очевидно, чем шире диапазон варьирования признака, тем больше должна быть и повторность опыта, и, на­оборот, при слабом варьировании учитываемого признака число вариантов опыта, т. е. их повторность, уменьшается. В такой же зависимости от размаха варьирования признаков находится и организация планирования минимально допустимого числа ис­пытаний.