конспект занятия по векторному пространству

Понятие размерности векторного пространства и базиса.

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статьелинейная зависимость системы векторов, свойства линейной зависимости и независимости.

Определение.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Определение.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n-мерных векторов.

Покажем, что размерность этого пространства равна n.

Возьмем систему из n единичных векторов вида 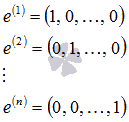  Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статьюранг матрицы: определение, методы нахождения). Следовательно, система векторов  линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе  равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы  являются базисом этого пространства.

Из последнего утверждения и определения базиса можно сделать вывод, что любая системаn-мерных векторов, число векторов в которой меньше n, не является базисом.

Теперь переставим местами первый и второй вектор системы . Легко показать, что полученная система векторов  также является базисом n-мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n. Таким образом, система из n векторов  линейно независима и является базисом n-мерного векторного пространства.

Если переставить местами другие векторы системы , то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Пример.

Может ли система векторов быть базисом векторного пространства?

Решение.

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема  исходной системы векторов является базисом).

Ответ:

нет, не может.

Пример.

Убедитесь, что векторы 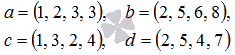  могут быть базисом четырехмерного векторного пространства.

Решение.

Составим матрицу, приняв ее строками исходные векторы: 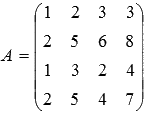  Найдем ранг матрицы методом Гаусса: 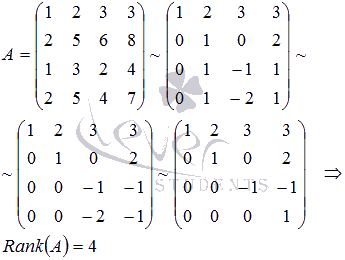  Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Ответ:

исходные векторы действительно являются базисом четырехмерного пространства.

Пример.

Составляют ли векторы  базис векторного пространства размерности 4?

Решение.

Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).

Ответ:

нет, не составляет.

Разложение вектора по базису векторного пространства.

Пусть произвольные векторы  являются базисом n-мерного векторного пространства. Если к ним добавить некоторый n-мерный вектор x, то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.

Теорема:Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказательство:Пусть  - базис n-мерного векторного пространства. Добавим к этим векторам n-мерный вектор x. Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где  - некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

Предположим, что существует еще одно разложение , где  - некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

Так как система базисных векторов  линейно независима, то поопределению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты  равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.

Определение.

Коэффициенты  называются координатами вектора x в базисе .

После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n-мерный вектор ». Это выражение означает, что мы рассматриваем вектор x n-мерного векторного пространства, координаты  которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .

Рассмотрим следующую задачу.

Пусть в некотором базисе n-мерного векторного пространства нам задана система из n линейно независимых векторов 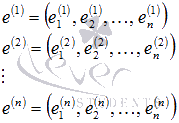  и вектор . Тогда векторы  также являются базисом этого векторного пространства.

Пусть нам требуется найти координаты вектора x в базисе . Обозначим эти координаты как .

Вектор x в базисе  имеет представление . Запишем это равенство в координатной форме: 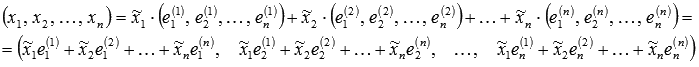  Это равенство равносильно системе из n линейных алгебраических уравнений с n неизвестными переменными :  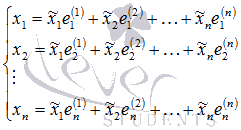 Основная матрица этой системы имеет вид 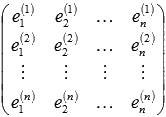  Обозначим ее буквой А. Строки матрицы А представляют собой векторы линейно независимой системы векторов , поэтому ранг этой матрицы равен n, следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, методом Крамера или матричным методом.

Так будут найдены искомые координаты  вектора x в базисе .

Пример.

В некотором базисе  четырехмерного векторного пространства задана линейно независимая система векторов 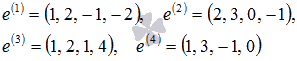  Известно, что . Найдите координаты вектора x в базисе .

Решение.

Так как система векторов  линейно независима по условию, то она является базисом четырехмерного пространства. Тогда равенство означает, что вектор x в базисе  имеет координаты . Обозначим координаты вектора x в базисе  как .

Система уравнений, задающая связь координат вектора x в базисах  и  имеет вид 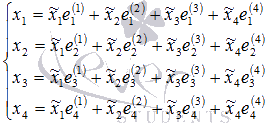  Подставляем в нее известные значения и находим искомые координаты :  

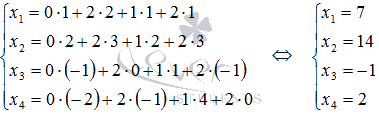
Ответ:

.

Связь между базисами.

Пусть в некотором базисе n-мерного векторного пространства заданы две линейно независимые системы векторов 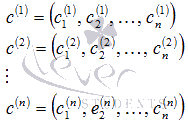  и 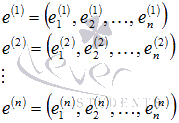  то есть, они тоже являются базисами этого пространства.

Если  - координаты вектора  в базисе , то связь координат  и  задается системой линейных уравнений (об этом мы говорили в предыдущем пункте): 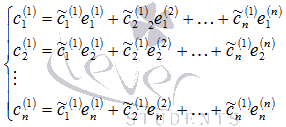  , которая в матричной форме может быть записана как

Аналогично для вектора  мы можем записать

Действуя дальше аналогично, получим

Предыдущие матричные равенства можно объединить в одно, которое по сути задает связь векторов двух различных базисов

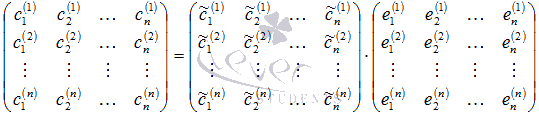
Аналогично мы можем выразить все векторы базиса  через базис :

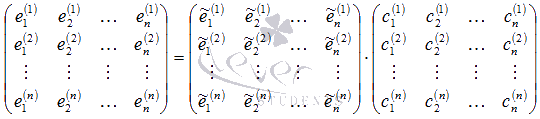
Определение.

Матрицу 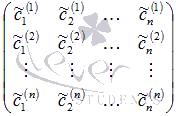 называют матрицей перехода от базиса  к базису , а матрицу 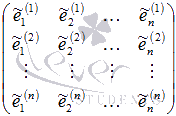 - матрицей перехода от базиса  к базису .

Из двух последних равенств видно, что 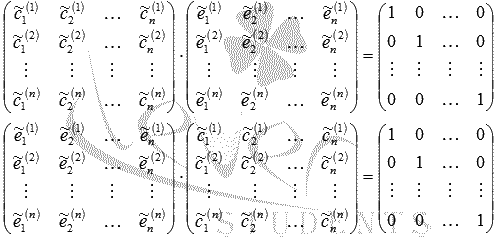  следовательно, матрицы перехода являются взаимно обратными.