§ 19. Свойства функций, непрерывных на отрезке

Первая теорема Больцано-Коши. Пусть функциянепрерывна на отрезкеи на концах этого отрезка принимает значения разных знаков. Тогда в интервале

найдется точка с, в которой функцияобращается в нуль, то есть.

Геометрический смысл этой теоремы состоит в том, что если непрерывная кривая переходит с одной стороны оси Ох на другую, то она пересекает эту ось.

Бернгард Больцано (1781-1848) – чешский философ и математик, доказал теорему в 1817 году. Огюстен Луи Коши (1789-1857) – знаменитый французский математик, доказал теорему независимо от Больцано в 1821 году. Этим ученым, особенно Коши, принадлежит заслуга обоснования математического анализа.

у

О

а

с

у =f(x)

b

x

Доказательство. Предположим для определенности, что. Обозначим отрезокчерези разделим его пополам точкой. Если, то теорема доказана и, в противном случае черезобозначим ту из половин отрезка, для которой.

Разделим отрезок пополам точкой. Если, то теорема доказана и, в противном случае черезобозначим ту из половин отрезка, для которой.

Продолжим этот процесс построения промежутков. При этом либо мы после конечного числа шагов наткнемся в качестве точки деления на точку, в которой функция обращается в нуль, и доказательство теоремы завершится, либо получим бесконечную последовательность вложенных один в другой отрезков. Тогда для n-го отрезкаимеем, причем длина егопри. По принципу вложенных отрезков Кантора (см. теорему 3 § 6) существует единственная точкас, принадлежащая всем этим отрезкам. Это точка. В силу непрерывности функциив точкеи. Переходя в неравенствахк пределу при, получим, что одновременнои, откуда. Теорема доказана.

Замечание. На доказанной теореме основан метод интервалов решения неравенств с одной переменной. Из теоремы следует, что функция, непрерывная на интервалеи не равная нулю ни в одной его точке, сохраняет знак на этом интервале. Поэтому, если функциянепрерывна в области своего определения, то точки, в которых она обращается в нуль, разбивают область ее определения на интервалы, в которых функция сохраняет знак. Для определения знакав интервале достаточно определить его в одной точке интервала. Объединение интервалов с требуемым знаком функции и является решением неравенства.

Пример 1. Решим неравенство.

Решение. Заметим, что функциянепрерывна в области своего определениякак элементарная функция. Она равна нулю в точкахи. Поэтомусохраняет знак в интервалах. Знак функции в каждом интервале можно определить с помощью пробной точки. Получим следующее распределение знаков:

• •

+ – + – + –1 1 2 3

Записываем ответ: .

Вторая теорема Больцано-Коши. Если функциянепрерывна на отрезкеи на концах этого отрезка принимает различные значения, то она принимает на этом отрезке любое значение, лежащее междуи.

Доказательство. Пусть для определенности. Надо доказать, что найдется точка, такая, что.

Рассмотрим вспомогательную функцию . Эта функция непрерывна на отрезкекак разность непрерывных функций,, т.е. на концах отрезкапринимает значения разных знаков. По 1-й теореме Больцано-Коши найдется точкатакая, что, т.е.или. Теорема доказана.

Замечания. 1) 1-я теорема Больцано-Коши является частным случаем 2-й теоремы Больцано-Коши, когдаиимеют разные знаки, а.

2) 1-ю и 2-ю теоремы Больцано-Коши называют также теоремами о промежуточных значениях.

3) Теоремы Больцано-Коши могут быть использованы при решении уравнений.

Пример 2. Докажем, что уравнениеимеет корень на отрезке.

Решение. Для функцииимеем, поэтому по 1-й теореме Больцано-Коши найдется точкатакая, что.

Значение корня можно найти и более точно. Поскольку ;и т.д.

1-я теорема Вейерштрасса. Если функциянепрерывна на отрезке, то она ограничена на этом отрезке.

Доказательство. Доказательство проведем методом от противного. Предположим, что функцияне ограничена на отрезке. Разобьем этот отрезок пополам. Тогда хотя бы на одной из половин отрезка функция будет неограниченной, обозначим эту половину через. Отрезокразделим пополам, ту его половину, на которой функция не ограничена, обозначим через. Если функция не ограничена на обеих половинах отрезка, то можно выбрать любую из них, например, правую. Продолжая описанный процесс деления отрезков, получим стягивающуюся последовательность вложенных отрезков

,

на каждом из которых функция не ограничена. По принципу вложенных отрезков существует единственная точка с, принадлежащая всем этим отрезкам. Поскольку, функциянепрерывна в этой точке, то есть. Поэтому существует окрестность, в которой функцияограничена. Так как длины отрезковстремятся к нулю, то при каком-тоnдлина отрезкастанет меньше, то есть будет. Поскольку функцияограничена в окрестности, она ограничена и на отрезке, что противоречит построению этого отрезка. Полученное противоречие показывает, что сделанное предположение о

◦ • • • ◦

с

неограниченности функции на отрезкеневерно. Поэтомуограничена на. Теорема доказана.

Обозначим множество значений функции , непрерывной на отрезке, через. По доказанной теореме это множество ограничено. Поэтому оно имеет точную нижнюю границуи точную верхнюю границу. Функцияне может принимать назначений, большихМи меньшихm. Может липринимать назначенияМ иm? Ответ дает

2-я теорема Вейерштрасса. Если функциянепрерывна на отрезке, то она достигает на этом отрезке своих точных нижней и верхней границ. Иными словами, найдутся точки, такие, чтои.

Доказательство. Рассмотрим случай точной верхней границы. Предположим противное, то есть что. Введем вспомогательную функцию. На отрезкезнаменатель в нуль не обращается, поэтому– непрерывная нафункция как частное двух непрерывных функций. По 1-й теореме Вейерштрасса она ограничена, то есть существует число, такое, что. Тогда, то естьМне является точной верхней границей значений функциина отрезке, что противоречит условию. Полученное противоречие показывает, что сделанное предположение неверно, то есть найдется точка, такая,.

Аналогично рассматривается случай точной нижней границы. Теорема доказана.

Следствие. Если функциянепрерывна на отрезке, то множеством ее значений является отрезок, гдеиМ– точные границы значений функции.

Доказательство. Действительно, по 2-й теореме Вейерштрассана, а по 2-й теореме Больцано-Коши любое числоявляется значением функциив некоторой точке, то есть. Что и требовалось доказать.

Теорема (о существовании и непрерывности обратной функции). Пусть функцияопределена на отрезке, возрастает и непрерывна на этом отрезке. Тогда на отрезкесуществует обратная функция, которая возрастает и непрерывна на этом отрезке.

Доказательство. В силу возрастания функцииее наименьшее значение равно, а наибольшее значение. По доказанному выше следствию совокупностью значенийявляется отрезок. Тогда любому значениюсоответствует значение, такое, что, причем значениеединственное в силу возрастания. Положим. Таким образом определена обратная функция, область определения которой – отрезок. Тем самым существование обратной функциидоказано.

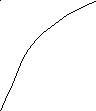
Докажем теперь, что функция возрастает. Пусть,,. Допустим, что. Тогда= =, что противоречит условию. Таким образом,– возрастающая функция.

Докажем непрерывность обратной функции в любой точке. Возьмемпроизвольно. Надо показать, что найдетсятакое, чтовыполняется неравенствоили, иначе,

у

f(b)

y =f(x)

f(a)

О а b х

выполняется неравенство.

Обозначим через. Тогда,, неравенстворавносильно неравенству. В силу возрастания. Возьмемтакое, что окрестность. Очевидно, что если, то, т.е., что и доказывает непрерывностьв точке. Поскольку– любая точка отрезка, функциянепрерывна на отрезке. Теорема доказана.

Замечание. Аналогичная теорема верна и для непрерывных убывающих на отрезкефункций. Утверждение остается верным и в случае, когда функция определена на бесконечном промежутке или не ограничена в области своего определения.