
- •§ 13. Определения Коши и Гейне предела функции, их эквивалентность. Критерий Коши существования предела
- •§ 14. Односторонние пределы
- •§ 15. Арифметические операции над функциями, имеющими предел
- •§ 16. Бесконечно малые и бесконечно большие функции. Первый замечательный предел
- •§ 17. Второй замечательный предел и его следствия
- •§ 18. Определение непрерывности функции. Арифметические операции над непрерывными функциями. Непрерывность сложной функции. Точки разрыва функции, их классификация
- •§ 19. Свойства функций, непрерывных на отрезке
- •§ 20. Равномерная непрерывность функций
§ 17. Второй замечательный предел и его следствия
Теорема 1 (2-й замечательный предел).
Справедливо равенство![]() ,
где
,
где![]() .
.
Доказательство. Воспользуемся
известным пределом![]() .
Докажем
.
Докажем
сначала, что
![]() .
Обозначим целую частьхчерезn:
.
Обозначим целую частьхчерезn:![]() .
Тогда
.
Тогда![]() и, следовательно,
и, следовательно,![]() и
и![]() .
Из неравенств
.
Из неравенств
![]() и
и![]() следует, что
следует, что
![]() .
.
Из неравенств
![]() и
и![]() следует, что
следует, что
![]() .
.
Таким образом,
![]() ,
где
,
где![]() .
.
Поскольку
![]() ,
,
![]()
и при
![]() и
и![]() ,
по теореме о промежуточной переменной
имеем, что
,
по теореме о промежуточной переменной
имеем, что![]() .
.
Рассмотрим теперь
![]() .
Положим
.
Положим![]() .
Когда
.
Когда![]() ,
то
,
то![]() и
и
![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=
=![]() =
=![]() .
.
Таким образом, и
![]() .
Значит, мы доказали, что
.
Значит, мы доказали, что![]() .
Теорема доказана.
.
Теорема доказана.
Обозначим
![]() .
Если
.
Если![]() ,
то
,
то![]() и 2-й замечательный предел примет вид
и 2-й замечательный предел примет вид![]() .
.
Следствия. 1)![]() .
В частности,
.
В частности,![]() .
.
2)
![]() .
В частности,
.
В частности,![]() .
.
3)
![]() .
.
Доказательство. 1)![]() .
.
При
![]() получаем частный случай.
получаем частный случай.
2) Положим
![]() при
при![]() .
Отсюда
.
Отсюда![]() .
Поэтому
.
Поэтому
![]() .
При
.
При![]() получаем частный случай.
получаем частный случай.
3) Заметим, что
![]() ,
поэтому
,
поэтому![]() .
Тогда
.
Тогда![]()
![]() .
Следствия доказаны.
.
Следствия доказаны.
Из следствий имеем: при
![]()
![]() ,
,![]() .
.
Примеры.
1)
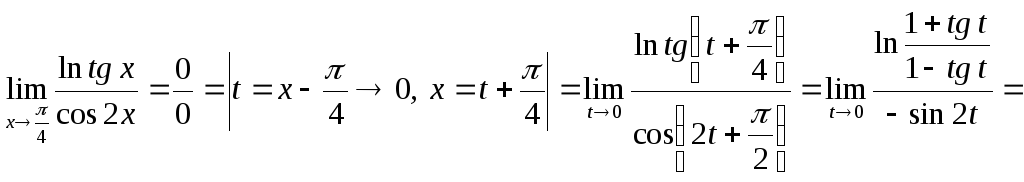
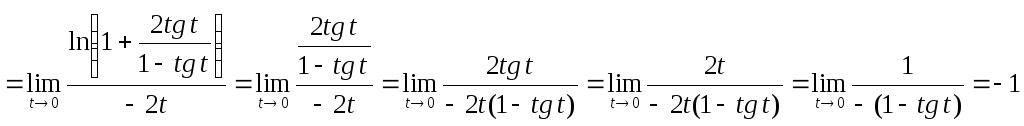 .
.
2)
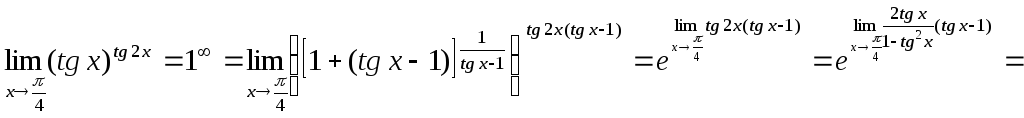
![]() .
.
§ 18. Определение непрерывности функции. Арифметические операции над непрерывными функциями. Непрерывность сложной функции. Точки разрыва функции, их классификация
Определение 1. Пусть функция![]() определена на промежуткеХи
определена на промежуткеХи![]() .
Функция
.
Функция![]() называетсянепрерывной в точке
называетсянепрерывной в точке![]() ,
если
,
если
![]() .
(18.1)
.
(18.1)
Равенство (18.1) можно записать иначе:
![]() ,
то есть для непрерывной функции знаки
предела и функции можно поменять местами.
,
то есть для непрерывной функции знаки
предела и функции можно поменять местами.
Очевидно, что о непрерывности функции
можно говорить лишь по отношению к тем
точкам
![]() ,
в которых функция определена, то есть
существует
,
в которых функция определена, то есть
существует![]() .
.
Пользуясь двумя определениями предела
функции, можно дать определения
непрерывности функции на языке
последовательностей и на языке
![]() .
.
Определение 2. Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если для любой последовательности
,
если для любой последовательности![]() значений аргументах, сходящейся
к
значений аргументах, сходящейся
к![]() ,
последовательность соответствующих
значений функции
,
последовательность соответствующих
значений функции![]() сходится к
сходится к![]() .
.
Определение 3. Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если для любого
,
если для любого![]() найдется
найдется![]() ,
такое, что для всехх, удовлетворяющих
неравенству
,
такое, что для всехх, удовлетворяющих
неравенству![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Определения 2 и 3 эквивалентны в силу теоремы 1 § 13.
Дадим еще одно определение непрерывности
функции в точке – на языке приращений.
Для этого положим
![]() и назовем эту величинуприращением
аргументах, а
и назовем эту величинуприращением
аргументах, а![]() –приращением функции в точке
–приращением функции в точке![]() .
.
Определение 4. Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если бесконечно малому приращению
аргумента в этой точке соответствует
бесконечно малое приращение функции,
то есть
,
если бесконечно малому приращению
аргумента в этой точке соответствует
бесконечно малое приращение функции,
то есть![]() .
.
Последнее условие означает, что
![]() ,
или
,
или![]() ,
или
,
или![]() ,
то есть определение 4 равносильно
определению 1, а значит и определениям
2 и 3.
,
то есть определение 4 равносильно
определению 1, а значит и определениям
2 и 3.
Определение 5. Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() справа (слева), если
справа (слева), если![]() (
(![]() ).
).
Теорема 1. Функция![]() непрерывна в точке
непрерывна в точке![]() тогда и только тогда, когда она непрерывна
в этой точке одновременно и справа, и
слева.
тогда и только тогда, когда она непрерывна
в этой точке одновременно и справа, и
слева.
Доказательство. Поскольку![]() существует тогда и только тогда, когда
существуют и равны односторонние пределы
существует тогда и только тогда, когда
существуют и равны односторонние пределы![]() и
и![]() ,
причем
,
причем![]() =
=
=
=![]() =
=![]() ,
то
,
то![]() тогда и только тогда, когда
тогда и только тогда, когда![]() =
=![]() =
=![]() .
Теорема доказана.
.
Теорема доказана.
Определение 6. Функция![]() называется непрерывной на промежуткеХ, если она непрерывна в каждой
точке этого промежутка.
называется непрерывной на промежуткеХ, если она непрерывна в каждой
точке этого промежутка.
Если
![]() ,
то при этом подразумевается непрерывность
,
то при этом подразумевается непрерывность![]() в точке
в точке![]() справа, а в точке
справа, а в точке![]() – слева.
– слева.
Теорема 2. Если функции![]() и
и![]() непрерывны в точке
непрерывны в точке![]() ,
то функции
,
то функции![]() тоже непрерывны в точке
тоже непрерывны в точке![]() .
Если, кроме того,
.
Если, кроме того,![]() ,
то и функция
,
то и функция![]() непрерывна в точке
непрерывна в точке![]() .
.
Доказательство. Следует из теоремы
1 § 15 и определения 1 непрерывности
функции в точке. Например,![]() ,
что и означает непрерывность функций
,
что и означает непрерывность функций![]() в точке
в точке![]() .
Остальные случаи рассматриваются
аналогично. Теорема доказана.
.
Остальные случаи рассматриваются
аналогично. Теорема доказана.
Теорема 3 (о непрерывности сложной
функции). Пусть![]() и пусть существует окрестность точки
и пусть существует окрестность точки![]() ,
в которой определена сложная функция.
Если функция
,
в которой определена сложная функция.
Если функция![]() непрерывна в точке
непрерывна в точке![]() ,
а функция
,
а функция![]() непрерывна в точке
непрерывна в точке![]() ,
то сложная функция
,
то сложная функция![]() непрерывна в точке
непрерывна в точке![]() .
.
Доказательство. В указанной в условии
теоремы окрестности возьмем любую
последовательность точек![]() ,
сходящуюся к точке
,
сходящуюся к точке![]() ,
и пусть
,
и пусть![]() .
Тогда, в силу непрерывности
.
Тогда, в силу непрерывности![]() в точке
в точке![]() ,
,![]() ,
то есть последовательность точек
,
то есть последовательность точек![]() сходится к точке
сходится к точке![]() .
Поэтому, в силу непрерывности
.
Поэтому, в силу непрерывности![]() в
точке
в
точке![]() ,
,![]() ,
то есть
,
то есть![]() .
.
Теорема доказана.
Определение 7. Точка![]() называетсяточкой разрыва функции
называетсяточкой разрыва функции![]() ,
если
,
если![]() определена в некоторой проколотой
окрестности точки
определена в некоторой проколотой
окрестности точки![]() и не выполняется условие
и не выполняется условие
![]() .
.
В этом случае говорят также, что функция
![]() является разрывной в точке
является разрывной в точке![]() ,
или терпит разрыв в точке
,
или терпит разрыв в точке![]() ,
или имеет разрыв в точке
,
или имеет разрыв в точке![]() .
.
Различают три типа точек разрыва.
1) Устранимый разрыв.
Определение 8. Точка![]() называется точкойустранимого
разрыва функции
называется точкойустранимого
разрыва функции![]() ,
если существует конечный
,
если существует конечный![]() ,
но либо функция не определена в точке
,
но либо функция не определена в точке![]() ,
либо
,
либо![]() .
.
Пример 1. Функция имеет устранимый разрыв в точке
имеет устранимый разрыв в точке![]() ,
,
так как
![]() .
Этот разрыв можно устранить, изменив
значение функции в точке
.
Этот разрыв можно устранить, изменив
значение функции в точке![]() и положив
и положив![]() .
.
Вообще, если в точке
![]() функция
функция![]() имеет устранимый разрыв, то достаточно
положить
имеет устранимый разрыв, то достаточно
положить![]() ,
чтобы функция стала непрерывной в точке
,
чтобы функция стала непрерывной в точке![]() .
Иными словами, для восстановления
непрерывности в точке
.
Иными словами, для восстановления
непрерывности в точке![]() надо изменить значение
надо изменить значение![]() в этой точке, если
в этой точке, если![]() ,
или доопределить
,
или доопределить![]() в точке
в точке![]() ,
если
,
если![]() .
.
2) Разрыв 1-го рода.
Определение 9. Точка![]() называется точкойразрыва 1-го
рода функции
называется точкойразрыва 1-го
рода функции![]() ,
если существуют конечные односторонние
пределы
,
если существуют конечные односторонние
пределы![]() и
и![]() ,
но
,
но![]()
![]()
![]() .
Разность
.
Разность![]()
![]() называютвеличиной скачка
называютвеличиной скачка ![]() в точке
в точке![]() .
.
Пример 2. Пусть![]() Тогда
Тогда![]() = –1,
= –1,![]() .
.![]() и
и![]() конечны, но не равны, поэтому точка
конечны, но не равны, поэтому точка![]() – точка разрыва 1-го рода. Величина
скачка равна
– точка разрыва 1-го рода. Величина
скачка равна![]() –
–![]() =
–1 – 0 = –1.
=
–1 – 0 = –1.
3) Разрыв 2-го рода.
Определение 10. Точка![]() называется точкойразрыва 2-го
рода функции
называется точкойразрыва 2-го
рода функции![]() ,
если хотя бы один из односторонних
пределов
,
если хотя бы один из односторонних
пределов![]() и
и![]() не
существует или бесконечен.
не
существует или бесконечен.
Пример 3. Пусть![]() .
Поскольку
.
Поскольку![]() ,
точка
,
точка![]() – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
Заметим, что
![]() ,
то есть бесконечен один односторонний
предел
,
то есть бесконечен один односторонний
предел![]() .
.
Пример 4. Пусть![]() .
Тогда
.
Тогда![]() не существует, поэтому
не существует, поэтому![]() – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
При исследовании функций на непрерывность полезна
Теорема 4. Любая элементарная функция непрерывна в области своего определения.
Без доказательства.
Напомним, что элементарной функцией
называется всякая функция, которая
может быть явным образом задана с помощью
формулы, содержащей лишь конечное число
арифметических операций и композиций
основных элементарных функций и
постоянных, а основными элементарными
функциями являются степенная
![]() ,
показательная
,
показательная![]() ,
логарифмическая
,
логарифмическая![]() ,
тригонометрические
,
тригонометрические![]()
![]() ,
обратные тригонометрические функции
,
обратные тригонометрические функции![]()
![]() .
.
Пример 5. Исследуем на непрерывность,
непрерывность слева и справа, установим
тип точек разрыва функции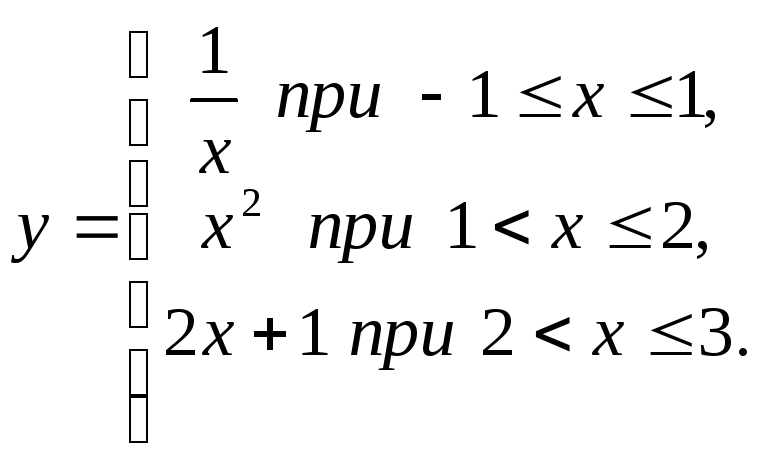
Решение. Заметим, что![]() .
Поскольку функция не определена при
.
Поскольку функция не определена при![]() и при
и при![]() ,
можно говорить только о непрерывности
справа в точке
,
можно говорить только о непрерывности
справа в точке![]() и о непрерывности слева в точке
и о непрерывности слева в точке![]() .
Имеем
.
Имеем
![]() функция
функция![]() непрерывна справа в точке
непрерывна справа в точке![]() ;
;
![]() функция
функция![]() непрерывна слева в точке
непрерывна слева в точке![]() .
.
Если
![]() ,
то
,
то![]() – непрерывна как элементарная функция
по теореме 4. Поскольку
– непрерывна как элементарная функция
по теореме 4. Поскольку![]() ,
то в точке
,
то в точке![]() функция
функция![]() имеет разрыв 2 рода, причем она имеет
разрыв 2 рода в этой точке и слева, и
справа.
имеет разрыв 2 рода, причем она имеет
разрыв 2 рода в этой точке и слева, и
справа.
Если
![]() ,
то
,
то![]() – непрерывна как элементарная функция.
– непрерывна как элементарная функция.
Если
![]() ,
то
,
то![]() – непрерывна как элементарная функция.
– непрерывна как элементарная функция.
Если
![]() ,
то
,
то![]() ,
,![]() ,
,![]() ,
т. е.
,
т. е.
существует
![]() ,
поэтому функция
,
поэтому функция![]() непрерывна в точке
непрерывна в точке![]() .
.
Если
![]() ,
то
,
то![]() ,
,![]() ,
,![]() ,
т.е. в точке
,
т.е. в точке![]() односторонние пределы существуют, но
не равны, поэтому в этой точке функция
односторонние пределы существуют, но
не равны, поэтому в этой точке функция![]() имеет разрыв 1 рода, величина скачка
равна 1. Поскольку
имеет разрыв 1 рода, величина скачка
равна 1. Поскольку![]() ,
то функция
,
то функция![]() в точке
в точке![]() непрерывна слева.
непрерывна слева.
Таким образом, функция
![]() непрерывна на множестве
непрерывна на множестве![]() ,
непрерывна справа в точке
,
непрерывна справа в точке![]() ,
непрерывна слева в точках
,
непрерывна слева в точках![]() и
и![]() ,
имеет разрыв 2 рода в точке
,
имеет разрыв 2 рода в точке![]() и разрыв 1 рода в точке
и разрыв 1 рода в точке![]() ,
величина скачка в этой точке равна 1.
,
величина скачка в этой точке равна 1.
Теорема 5 (о точках разрыва монотонной
функции). Если функция![]() монотонна на интервале
монотонна на интервале![]() ,
точка
,
точка![]() является точкой разрыва
является точкой разрыва![]() ,
тос– точка разрыва 1-го рода.
,
тос– точка разрыва 1-го рода.
Д
• • •![]() не убывает на интервале
не убывает на интервале![]() .
Рассмотрим интервал
.
Рассмотрим интервал![]() .Для
всех значенийх
.Для
всех значенийх![]() имеем
имеем![]() ,
т.е.
,
т.е.![]() ограничена сверху. В силу ограниченности
сверху множества
ограничена сверху. В силу ограниченности
сверху множества![]() существует
существует![]() .
Покажем, что
.
Покажем, что![]() .
Действительно,
.
Действительно,![]() для всех
для всех![]() ,
так какА – верхняя граница значений
,
так какА – верхняя граница значений![]() .
Возьмем
.
Возьмем![]() произвольно. ПосколькуА – точная
верхняя граница значений
произвольно. ПосколькуА – точная
верхняя граница значений![]() ,
найдется
,
найдется![]() такое, что
такое, что![]() .
Тогда для
.
Тогда для![]() тем более
тем более![]() в силу возрастания функции. Таким
образом, для всех
в силу возрастания функции. Таким
образом, для всех![]()
![]() ,
для
,
для![]()
![]() и, значит, для
и, значит, для![]()
![]() ,
т.е.
,
т.е.![]() .
Взяв
.
Взяв![]() ,
получим, что для всехх, таких, что
,
получим, что для всехх, таких, что![]() имеем
имеем![]() .
А это и означает, что
.
А это и означает, что![]() .
.
Таким
образом, доказано существование
![]() .
.

![]() Аналогично доказывается
существование
Аналогично доказывается
существование![]() .
.
В силу существования
![]() и
и![]() ,с– точка разрыва 1 рода.
,с– точка разрыва 1 рода.
Аналогично рассматривается случай невозрастающей функции.
Теорема доказана.
Таким образом, монотонная функция может иметь только точки разрыва 1-го рода.
