Разобранные примеры по теме Магитное поле

Задача 5.

Электрон в однородном магнитном поле с индукцией В = 0,1 Тл движется по окружности. Найти силу кругового тока I, создаваемого движущимся электроном.

Решение.

Так как электрон движется по окружности, то вектор скорости электрона перпендикулярен к вектору магнитной индукции . Тогда сила Лоренца , направленная всегда перпендикулярно к скорости, сообщает электрону центростремительное ускорение , где R – радиус окружности, по которой движется электрон в магнитном поле.

Согласно второму закону Ньютона или

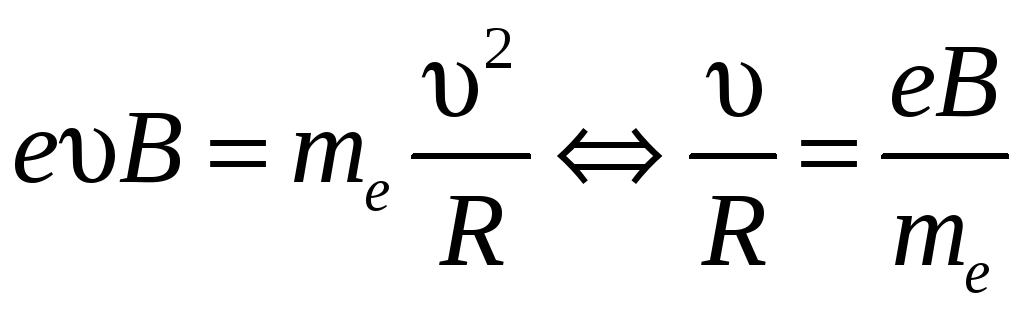. (1)

Движение электрона по окружности эквивалентно круговому току. Если электрон остановится, то исчезнет и круговой ток. Таким образом, изменение кинетической энергии электрона можно связать с работой по перемещению контура с током :

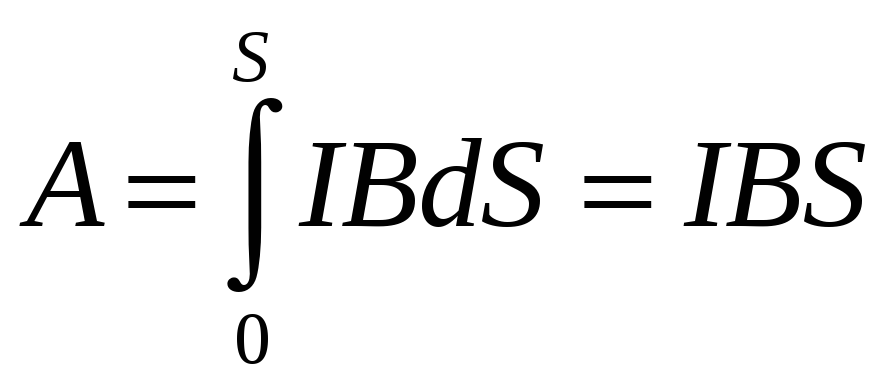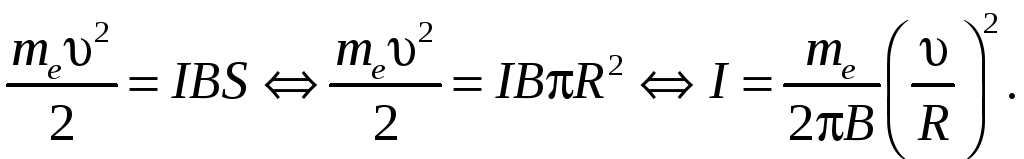(2)

Подставив (1) в (2), найдем искомую силу кругового тока:

Ответ:

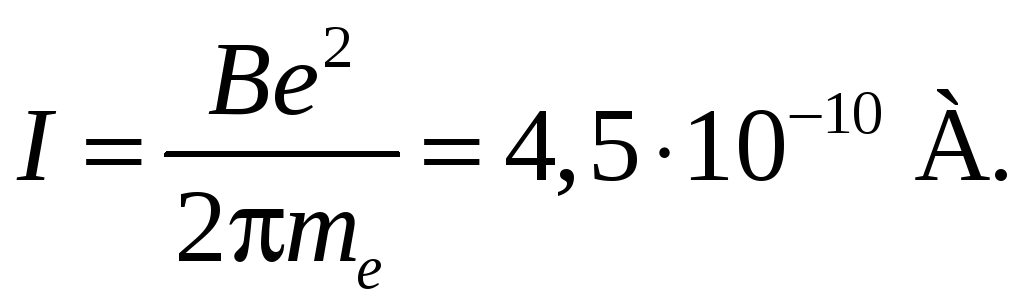
Задача 27.

Из какого материала изготовлена обмотка соленоида длиной l = 0,3 м, если диаметр соленоида D = 0,05 м, напряженность магнитного поля на его оcи H = 15 А/м, напряжение на концах обмотки U = 0,9 В? Диаметр провода d = 10^-3 м.

Решение.

Пусть соленоид имеет N витков. Каждый виток соленоида представляет собой проводник. Сопротивление такого проводника находится по формуле

, (1)

где l₁ – длина одного витка соленоида, S₁ – площадь поперечного сечения витка соленоида, ρ – удельное сопротивление материала, из которого изготовлена обмотка соленоида.

Так как диаметр соленоида равен D, то диаметр витка соленоида тоже равен D. Следовательно, длина одного витка соленоида

. (2)

Поскольку диаметр провода равен d, то площадь поперечного сечения витка соленоида

. (3)

Подставив (2) и (3) в (1), получим

(4)

Так как соленоид состоит из N витков, то сопротивление всего соленоида

(5)

Напряженность магнитного поля на оси соленоида

, (6)

где I – ток, идущий по обмотке соленоида.

По закону Ома

(7)

После подстановки выражения (7) для тока в выражение (6) для напряженности магнитного поля на оси соленоида, выразим искомое значение удельного сопротивления материала ρ, из которого изготовлена обмотка соленоида:

Ответ:

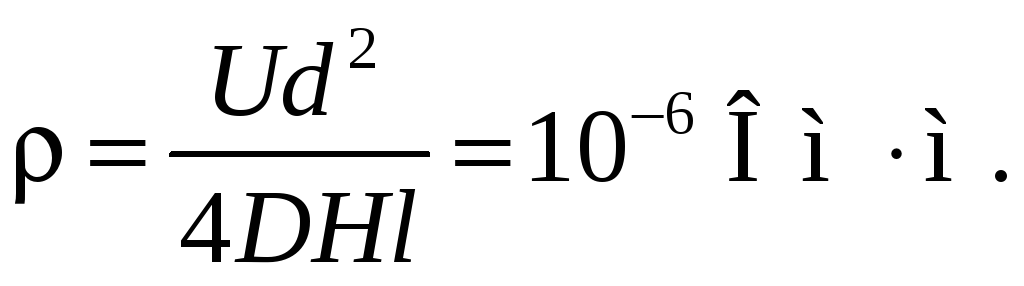
Задача 21.

Под длинной горизонтальной шиной на двух одинаковых пружинах (жесткость каждой равна k) подвешен провод длиной l. Когда в шине и проводе токи отсутствуют, расстояние между ними равно h. Найдите расстояние между шиной и проводом, если по шине течет ток I, а по проводу i. Провод не может выйти из вертикальной плоскости.

Решение.

Жесткость пружин, соединенных параллельно, равна сумме жесткостей отдельных пружин. Следовательно, жесткость двух одинаковых пружин в нашей задаче равна 2k.

В случае, когда токи в шине и проводе отсутствуют, на провод действуют только сила тяжести и силы упругости со стороны пружин. По второму закону Ньютона для провода:

(1)

где – растяжение пружины в случае отсутствия токов I и i.

Пусть – длина пружины в нерастянутом состоянии, тогда

(2)

Подставив (2) в (1), получим:

(3)

а) Пусть токи I и i текут в одну сторону. Тогда, помимо силы тяжести и сил упругости со стороны пружин, на провод со стороны шины будет действовать сила Ампера, притягивающая провод к шине:

(4)

где В – индукция магнитного поля, созданного шиной с током I.

По формуле для индукции магнитного поля прямого проводника с током находим индукцию магнитного поля шины, действующего на провод:

(5)

где x – расстояние от шины до провода.

Подставив (5) в (4) получим

(6)

По второму закону Ньютона для провода:

(7)

где – растяжение пружины,

(8)

Подставив (8) в (7), получим:

При уравнение (7) решений не имеет, т.е. провод притянется к шине.

б) Пусть токи I и i текут в противоположных направлениях. Тогда, помимо силы тяжести и сил упругости со стороны пружин, на провод со стороны шины будет действовать сила Ампера, отталкивающая провод от шины:

(4)

где В – индукция магнитного поля, созданного шиной с током I.

По формуле для индукции магнитного поля прямого проводника с током находим индукцию магнитного поля шины, действующего на провод:

(5)

где x – расстояние от шины до провода.

Подставив (5) в (4) получим

(6)

По второму закону Ньютона для провода:

(7)

где – растяжение пружины,

(8)

Подставив (8) в (7), получим:

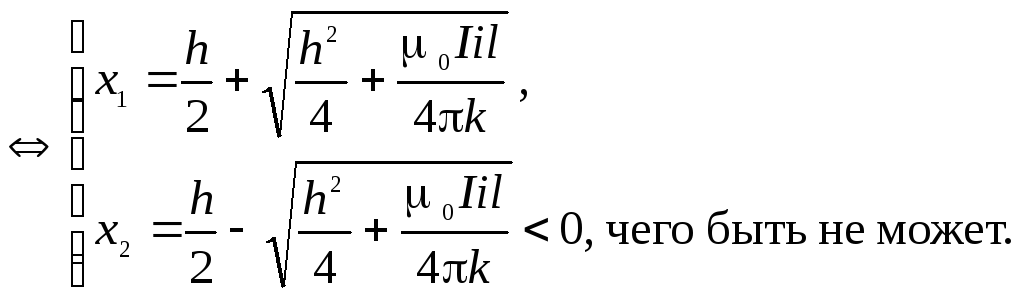
Таким образом, имеется одно решение

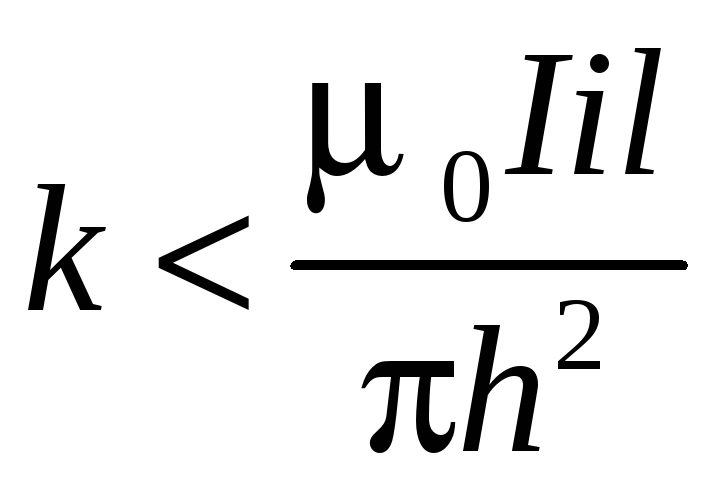Ответ: а) Если токи I и i текут в одну сторону, то расстояние между шиной и проводом может быть: (устойчивое равновесие) или (неустойчивое равновесие). Если , т.е. , провод притянется к шине.

б) Если токи I и i текут в противоположных направлениях, то провод отталкивается от шины и будет в устойчивом равновесии на расстоянии .

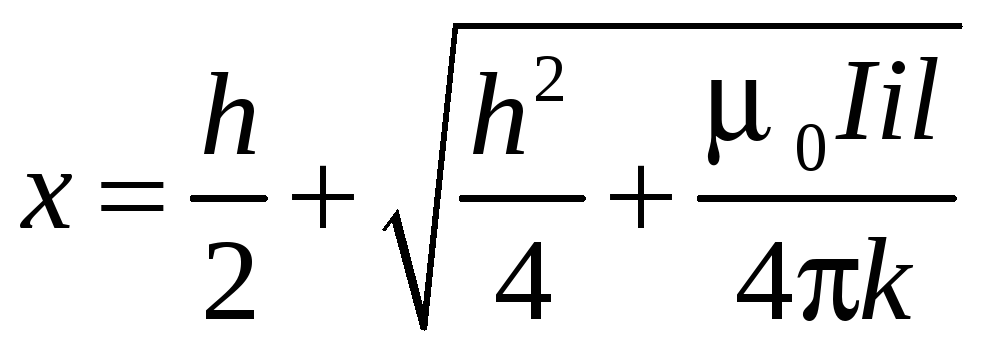Задача 29. 

Д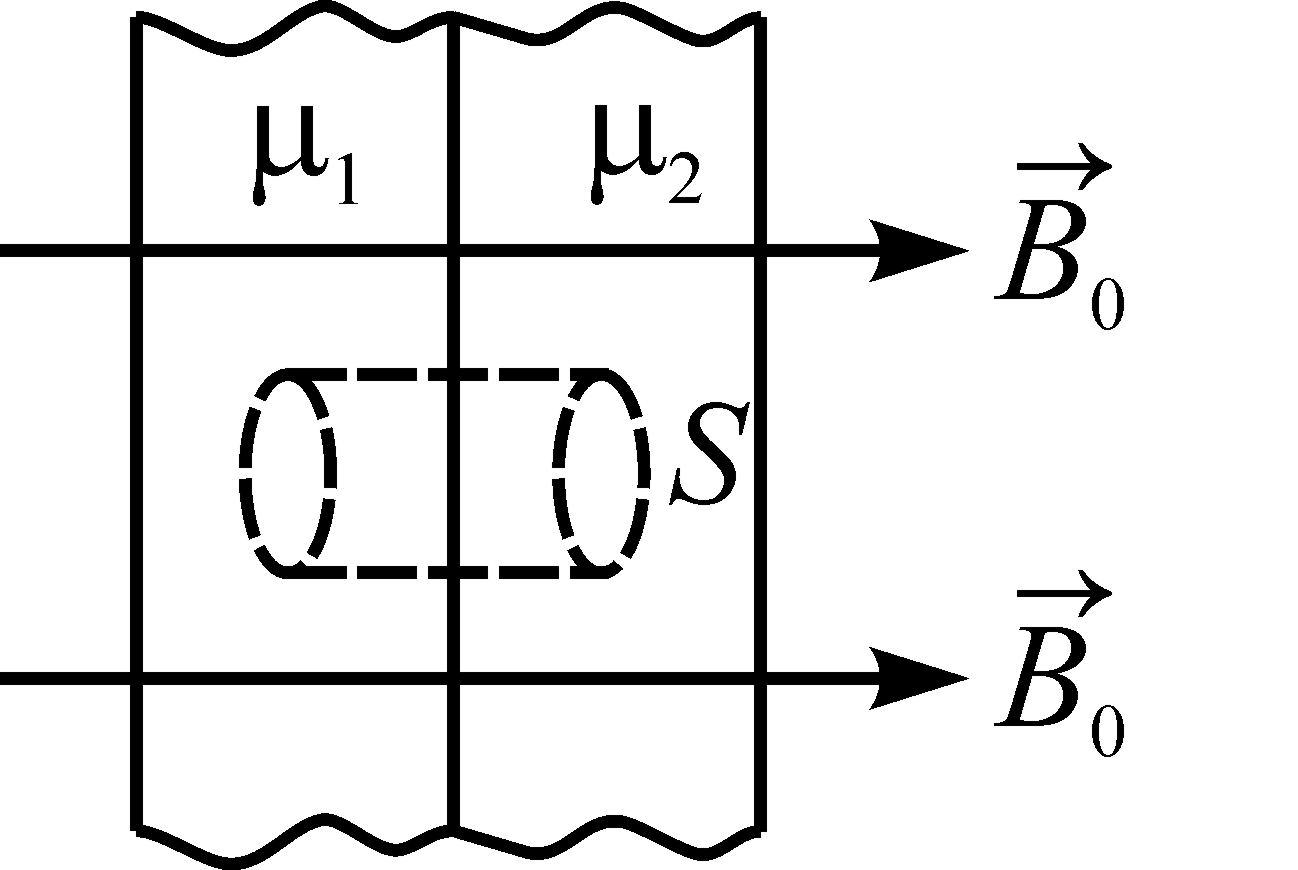ве пластины из магнетиков с проницаемостями µ₁ и µ₂ сложены вместе и помещены в перпендикулярное к ним однородное поле с индукцией В₀ (см. рис.). Штриховой линией показана воображаемая цилиндрическая поверхность с образующими, параллельными В₀, и основаниями площади S, перпендикулярными к В₀. Чему равны поток Ф_В вектора В и поток Ф_Н вектора Н через эту поверхность?

Решение.

Поток вектора магнитной индукции через цилиндрическую поверхность равен сумме потоков через основания и через боковую поверхность цилиндра:

Аналогично, для потока напряженности магнитного поля через цилиндрическую поверхность:

Будем считать первым основанием цилиндра основание, лежащее в пластине из магнетика с проницаемостью µ₁, а вторым – основание, лежащее в пластине из магнетика с проницаемостью µ₂.

В общем случае

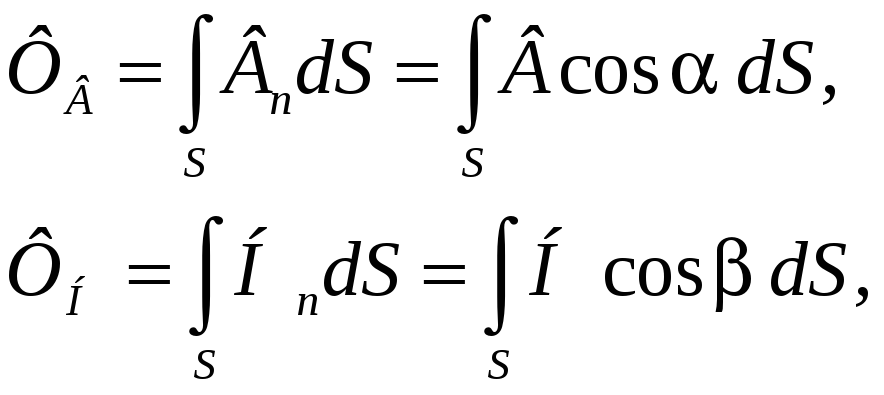
где α – угол между вектором магнитной индукции и нормалью к поверхности S, β – угол между вектором напряженности магнитного поля и нормалью к поверхности S.

Таким образом, необходимо найти нормальные составляющие вектора магнитной индукции и вектора напряженности магнитной индукции через основания цилиндра и через его боковую поверхность.

Так как на границе раздела двух магнетиков нормальные составляющие вектора магнитной индукции не меняются, то внутри магнетиков магнитная индукция равна и по направлению совпадает с магнитной индукцией однородного поля, в которое помещены пластины. Таким образом, магнитная индукция внутри пластин магнетиков перпендикулярна к ним, а значит, перпендикулярна к основаниям цилиндра и параллельна образующим цилиндра. Последнее означает, что _. Тогда

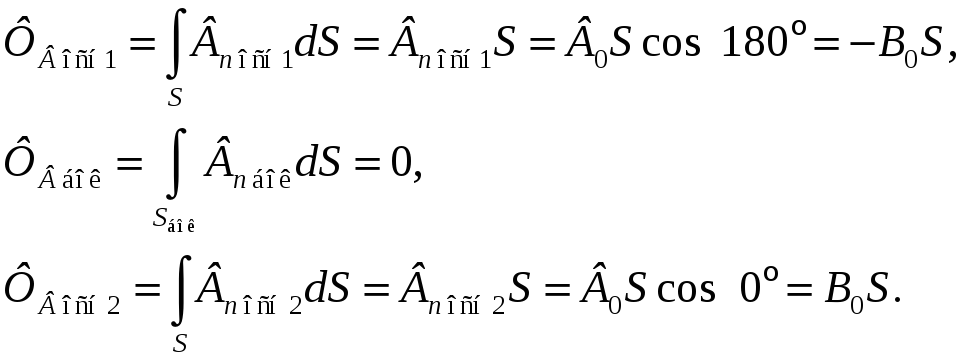
В итоге получим

Найдем теперь поток напряженности магнитного поля Ф_Н.

В первом магне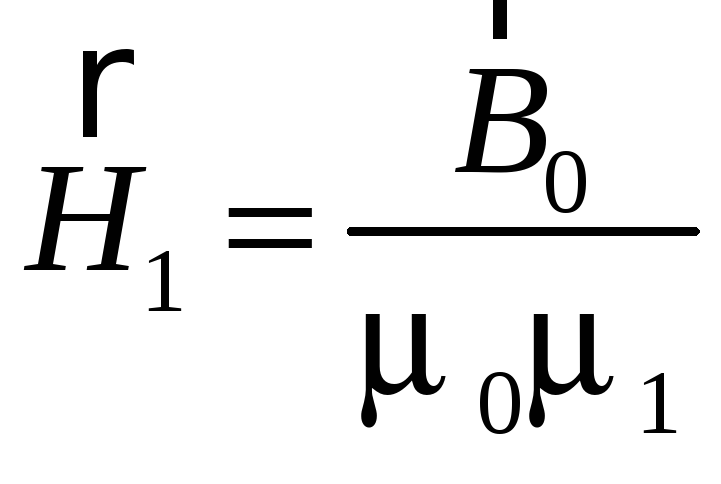тике , во втором магнетике . Тогда

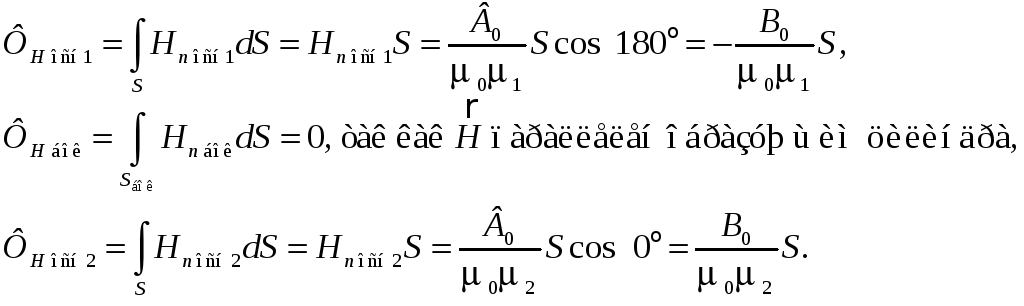
В итоге

Ответ: , .

8