10. Правила Кирхгофа для цепей переменного тока

Первое правило Кирхгофа:

Алгебраическая сумма комплексных токов в узле электрической цепи равна нулю:

Второе правило Кирхгофа:

Алгебраическая сумма комплексных значений э.д.с. в любом контуре электрической цепи равна алгебраической сумме комплексных значений падений напряжений на всех приемниках этого контура:

,

где n – число источников э.д.с. в контуре;

m – число приемников в контуре;

– комплексные падения напряжения на i-том приемнике контура.

Уравнения для цепей переменного тока по правилам Кирхгофа составляются точно так же, как и для цепей постоянного тока.

Правила Кирхгофа справедливы так же для мгновенных значений токов, э.д.с. и напряжений.

11. Полная цепь переменного тока

Полной цепью переменного тока называется цепь, содержащая источник, а также активный, индуктивный и емкостной элементы. Такие цепи часто называют цепями RLC.

Последовательное соединение элементов RLC

Пусть в такой цепи протекает ток

Ур-ие электрического состояния цепи для мгновенных напряжений имеет вид:

Построим векторную диаграмму, соответствующую этому уравнению.

При построении векторных диаграмм стрелки векторов направляются в сторону возрастающего потенциала.

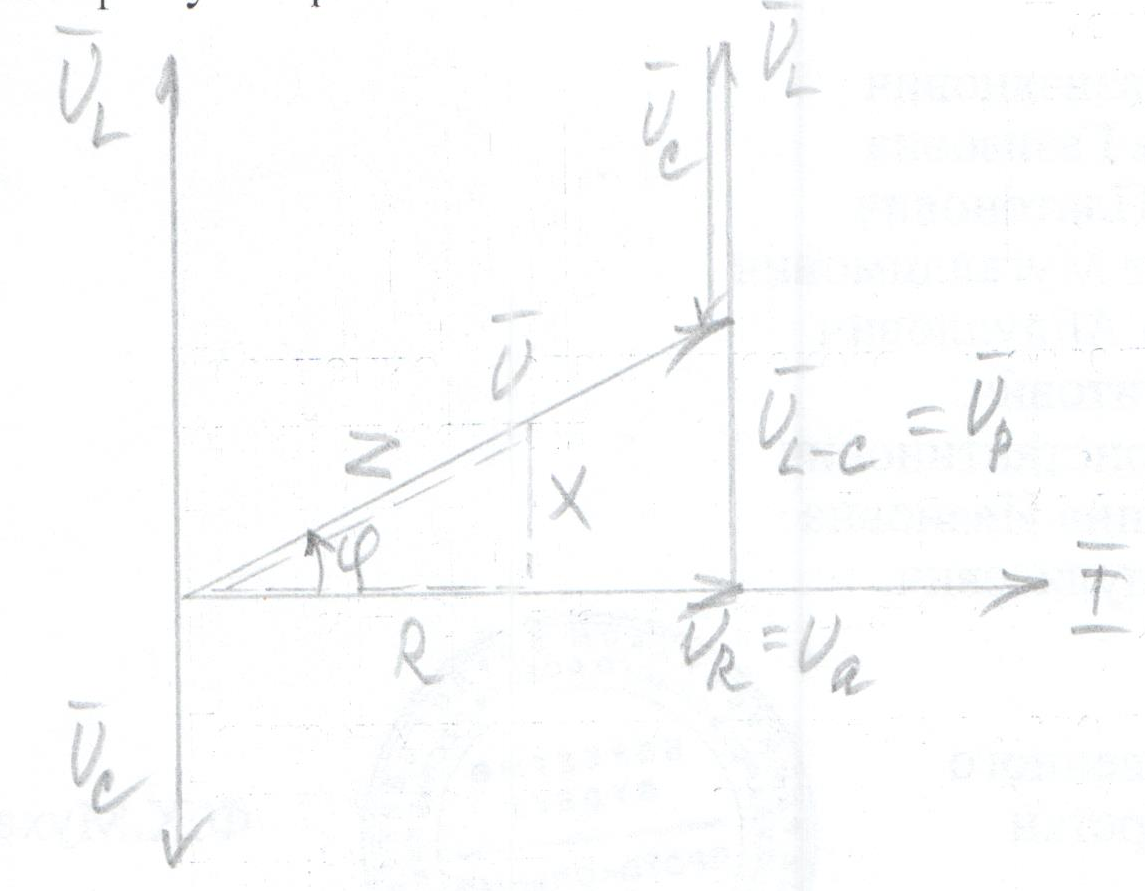
Найдем сумму векторов .

Результирующий вектор равен напряжению источника.

Вектор можно разложить на составляющие: = и , которые называют активной и реактивной составляющей вектора напряжения . Точно также можно разложить и вектор тока .

Векторы , и образуют прямоугольный треугольник (треугольник напряжений), из которого

.

Поделив напряжение на ток, получим модуль полного сопротивления

,

где Z – модуль (численное значение) полного сопротивления.

Х = Х_L – Х_С – реактивное сопротивление электрической цепи.

В нашем случае Х_L > Х_С (нагрузка активно-индуктивная). В случае, если Х_L < Х_С (нагрузка активно-емкостная), .

На векторной диаграмме этому выражению соответствует треугольник сопротивлений (показан пунктиром).

Из треугольника сопротивлений можно определить угол сдвига фаз между током и напряжением. На векторной диаграмме угол φ отсчитывается от вектора I к вектору U. Положительным является направление против часовой стрелки.

или , отсюда

.

Из формулы видно, что угол сдвига фаз зависит только от параметров цепи RLC и не зависит от величины I и U. Этот угол можно изменять, изменяя параметры цепи.

Если Х_L > Х_С (как в нашем случае), реактивное сопротивление положительно, и сопротивление цепи носит активно-индуктивный характер. Если Х_L < Х_С, реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостный характер.

Треугольник напряжений и треугольник сопротивлений в этом случае выглядят:

Закон Ома в комплексной форме:

или

– полное комплексное сопротивление

Комплексное полное сопротивление

Модуль полного сопротивления

,

Т.О, модуль полного сопротивления цепи равен отношению модулей действующих значений напряжения и тока, а аргумент комплексного сопротивления φ – сдвигу фаз меду напряжением и током.

Из треугольника сопротивлений видны следующие соотношения:

, .

Мощность в цепи RLC

Знак φ определяется по формуле

Соответственно

– активная мощность

– реактивная мощность

– полная мощность.

– коэф-нт мощности (показывает долю активной мощности в полной мощности).

Параллельное соединение элементов RLC

Пусть к данной цепи приложено напряжение

Его комплексное действующее значение

В соответствии с 1 правилом Кирхгофа для комплексных действующих значений токов

,

где – активная проводимость,

– индуктивная проводимость,

– емкостная проводимость,

– комплексная проводимость.

Все проводимости измеряются в сименсах (См).

Закон Ома в комплексной форме: .

– если нагрузка индуктивная (Х_L > Х_С);

– если нагрузка емкостная (Х_L < Х_С).