4. Электрическая цепь с активным сопротивлением

Электрический ток проводимости в металлах представляет собой направленное движение свободных электронов. Скорость электронов и направление их движения определяется значением и полярностью приложенного к проводнику напряжения.

При движении электроны сталкиваются с атомами проводника, и их кинетическая энергия превращается в тепловую энергию, которая идет на нагрев проводника и рассеивание в окружающую среду. Этот активный процесс является необратимым и количественно определяется сопротивлением R. Поэтому его называют активным сопротивлением. Как правило, различают активное и омическое сопротивления. При рассмотрении цепей переменного тока сопротивление R называют активным, так как оно больше сопротивления постоянному току. При рассмотрении цепей постоянного тока сопротивление R называют омическим.

(Если через один и тот же проводник пропускать переменный и постоянный ток, то для того, чтобы выделилось одно и то же количество теплоты, величина переменного тока должна быть больше, чем постоянного).

Элементы электрической цепи, обладающие только активным сопротивлением R, называют резисторами. Все элементы электрической цепи – провода, обмотки, реостаты – обладают активным сопротивлением, все они нагреваются при пропускании тока.

Кроме активного сопротивления существует еще индуктивное, емкостное, реактивное, полное.

Пусть к зажимам цепи с активным сопротивлением R приложено напряжение источника питания.

По закону Ома для мгновенных значений для этой цепи

, отсюда

– закон Ома для амплитудных значений.

Разделив левую и правую части этого выражения на , получим

– закон Ома для действующих значений

( , – связь действующего значения с амплитудным).

– закон Ома в комплексной форме.

Комплексное действующее значение тока .

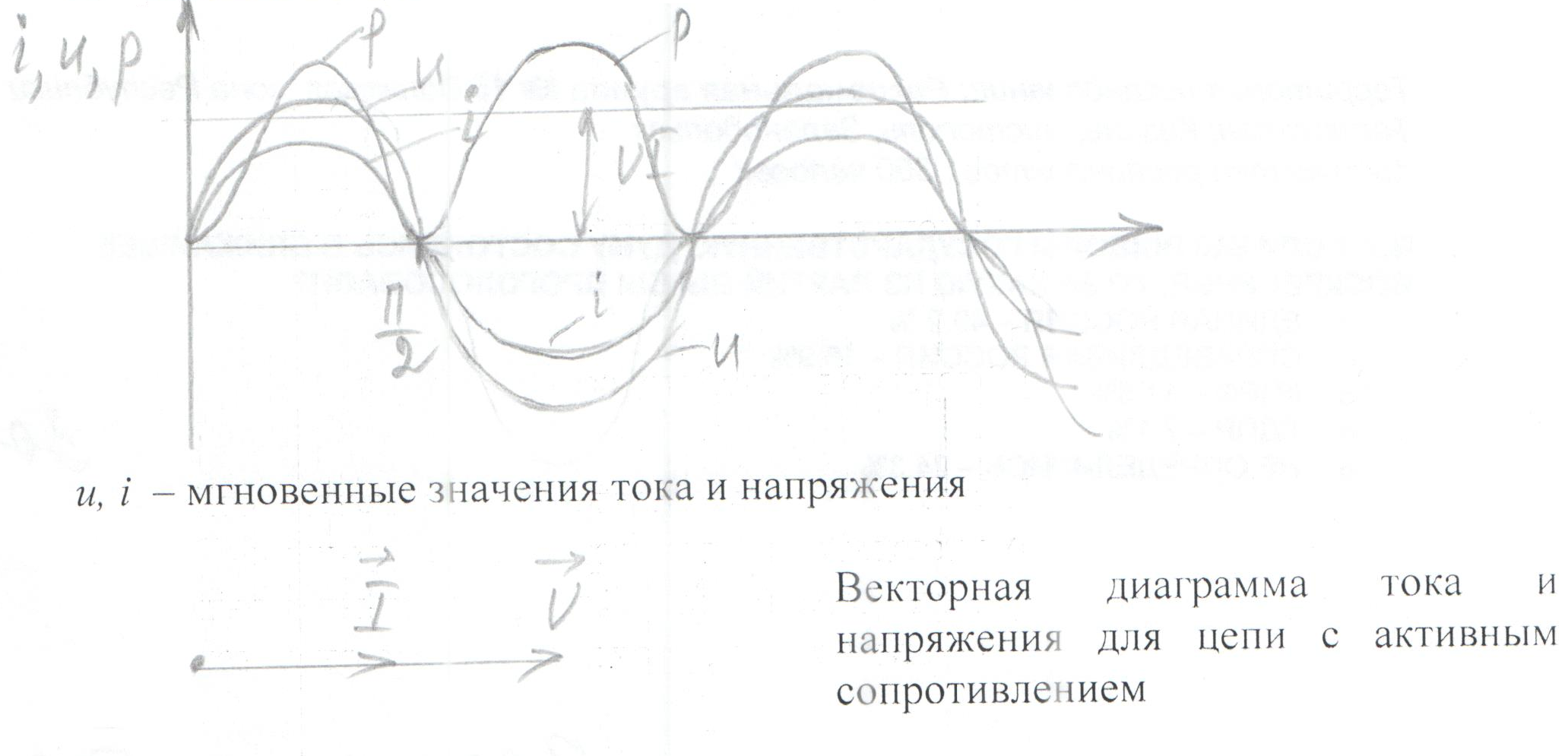
Поскольку ток и напряжение совпадают по фазе, как видно из формул для мгновенных значений, то можно представить изменение тока и напряжения на временной диаграмме следующим образом:

5. Мощность в цепи с активным сопротивлением

Мгновенная мощность

Мощность определяет скорость расхода энергии, и для цепей переменного тока также является переменной величиной.

Т.к. , то

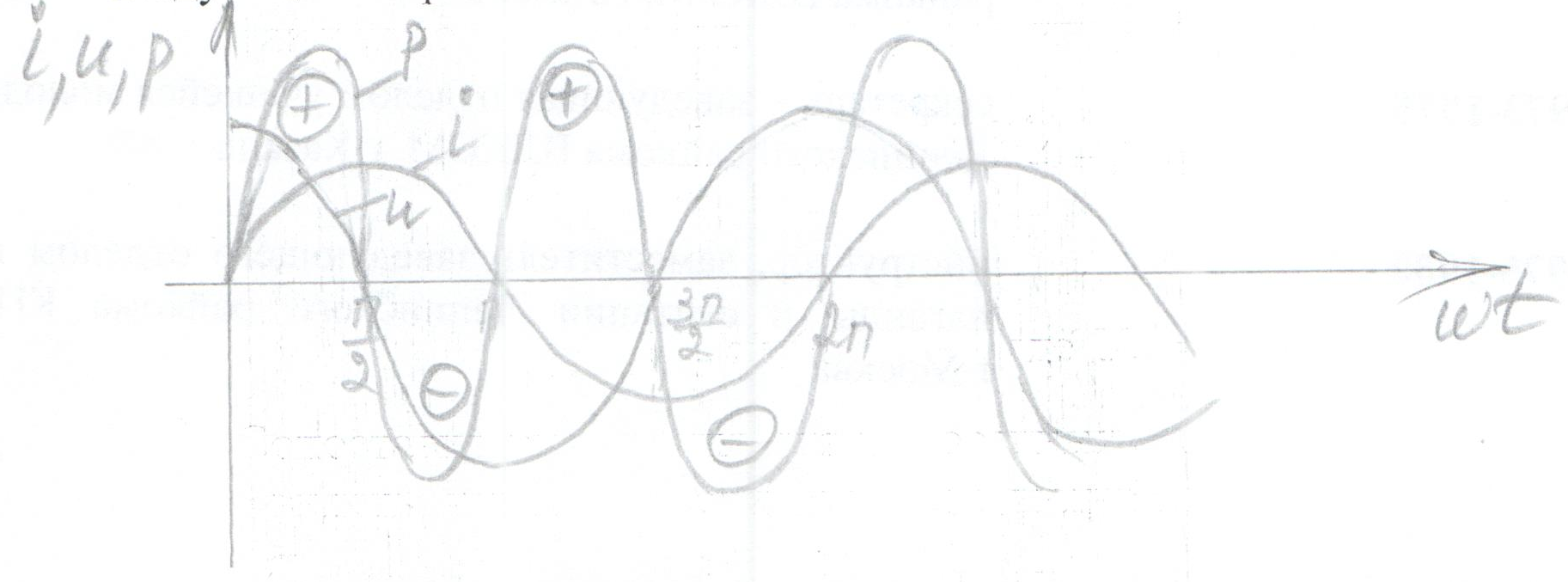
Из формулы видно:мгновенная мощность остается всегда положительной и колеблется около уровня UI (см. график).

С энергетической точки зрения, положительная мощность – это мощность, которая поступает из генератора в нагрузку, а отрицательная – та, которая возвращается обратно. Первая мощность называется активной, вторая – реактивной. Через активное сопротивление проходит только активная мощность.

Средняя мощность

Для определения расхода энергии за длительное время пользуются средним значением мощности. Такую мощность еще называют активной

P = UI.

Активная мощность обозначается [P], единица измерения Ватт (Вт), (кВт), (МВт).

6. Электрическая цепь с индуктивностью

Индуктивность можно определить как меру магнитной инерции элемента в отношении электромагнитного поля. По смыслу индуктивность в электротехнике можно сравнить с массой в механике. Чем больше индуктивность элемента, тем медленнее и тем большую энергию магнитного поля он запасает.

Индуктивностью, индуктивным сопротивлением обладают в разной мере все элементы электрической цепи переменного тока. Особенно велика она у обмоток или катушек, состоящих из большого числа витков. В цепях постоянного тока индуктивность равна нулю, поскольку ток не меняется со временем и проявляется лишь при переходных режимах.

Рассмотрим электрическую цепь, состоящую из источника и катушки индуктивности.

Под действием синусоидального напряжения в цепи протекает синусоидальный ток

В результате этого вокруг катушки возникает переменное магнитное поле, и в катушке наводится э.д.с. самоиндукции.

Если R = 0, то напряжение источника целиком идет на уравновешивание этой э.д.с. Следовательно,

Т.к. по закону электромагнитной индукции , то

или , где .

Сопоставив выражения для мгновенных значений тока и напряжения, можно видеть, что напряжение в цепи с индуктивностью опережает по фазе ток на .

Т.О, временная диаграмма для тока и напряжения выглядит:

Векторная диаграмма тока и напряжения для цепи с индуктивностью

,

– индуктивное сопротивление цепи;

: видно, что с увеличением частоты увеличивается индуктивное сопротивление.

Закон Ома для цепи с индуктивностью

Закон Ома для амплитудных значений для цепи с индуктивностью: .

Разделив левую и правую части этого выражения на , получим закон Ома для действующих значений .

Закон Ома в комплексной форме

,

j обеспечивает сдвиг фаз на между I и U на комплексной плоскости.