Экзамен / Точно билеты ОТС Удачи(2020)

Экзаменационный билет №20

1. Формирователь модулирующих символов (ФМС) для сигналов КАМ16. Сигнальное созвездие КАМ-16. Понятие о коде Грея.

Число точек в созвездии равное 16 представляем в виде , где . Определяем величину – число дискретных значений, которые могут принимать координаты и точек на

сигнальном созвездии, т. е. . Используя (2m −1− M )h, m = 1, 2, ..., M (определение дискретных значений), находим значения координат точек созвездия КАМ-16 на осях I и Q:

–3h,– h ,h ,3h ,где h – заданная величина (34)

Итак, сигнальное созвездие для КАМ-16 содержит 16 точек. Известно также, что существует различных блоков (последовательностей) из 4 двоичных символов, отличающихся друг от друга хотя бы одним символом (битом). Отсюда следует, что каждую точку на сигнальном

созвездии можно связать с одним из 16 символьных блоков. Соответствие между 16 различными блоками из 4 символов (битов) и 16 точками сигнального созвездия можно осуществлять различными способами.

Наиболее рациональное соответствие получается при использовании так называемого ​кода Грея​, когда соседним точкам на сигнальном созвездии соответствуют блоки, отличающиеся друг от друга ​только одним ​символом​. Сигнальное созвездие для КАМ-16 изображено на рис. 14.

Рис. 14. Сигнальное созвездие для КАМ-16

Из 19 билета

Наиболее известным и часто применяемым манипуляционным кодом является код Грея, при котором сигнальным точкам, находящихся на минимальном евклидовом расстоянии, ставятся в соответствие кодовые слова, отличающиеся только одним элементом. Существуют коды Грея

для КАМ сигналов с 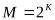при четном 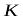. На рис. приведен пример манипуляционного кода Грея для КАМ-1

2. Прямая и обратная теоремы Шеннона о кодировании в канале с помехами. Условная энтропия между входом и выходом в канале и взаимная информация входа и выхода. Информационная емкость и пропускная способность канала связи.

R -​скорость передачи сообщений

C -пропускная способность канала

Per - средняя вероятность ошибки декодирования блока

Rer,max -​максимальная вероятность ошибки декодирования блока

Прямая теорема Шеннона :

Сложная но правильная версия:

Если скорость передачи сообщений меньше пропускной способности канала связи (R<C), то существуют коды Loading… и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности, то естьLoading… при Loading…

Если попросят пояснить:

Для канала с помехами всегда можно найти такую систему кодирования, при которой сообщения будут переданы со сколь угодно большой ​степенью верности​, если только производительность источника не превышает​​пропускной способности канала​.

Обратная теорема:

Если скорость передачи больше пропускной способности, то есть R>C, то не существует таких способов передачи, при которых вероятность ошибки стремится к нулю Loading… при увеличении длины передаваемого блока, Loading…

Условная энтропия между входом и выходом в канале и взаимная информация входа и выхода

Говорят, что канал симметричен по входу, если все строки матрицы Р являются перестановками одного и того же множеств​а чисел Loading…

Для такого канала условная энтропия =

имеет одинаковое значение для всех сигналов bk(k-кононическая) принадлежащих В., Где p(y/b) условная вероятность перехода входного сигнала bk в выходной сигнал у в определенный момент времени.

Среднюю взаимную информацию между входной и выходной вероятностными схемами для симметричного по входу канала можно записать в виде:

Экзаменационный билет №21Классификация случайных сигналов по виду закона распределения. Нормальный закон: формула одномерной ПРВинтеграл вероятности

1. Классификация случайных сигналов по виду закона распределения. Нормальный закон: формула одномерной ПРВ(плотность распределения вероятности), график одномерной ПРВ и ФРВ(функция распределения вероятности). Интеграл вероятностей Ф(*) и функция ошибок

Q(*).

Случайные сигналы подразделяют на стационарные и нестационарные. Случайные стационарные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса. Что касается случайных нестационарных сигналов, то их общепринятой классификации не существует. Как правило, из них выделяют различные группы сигналов по особенностям их нестационарности.

Нормальное распределение относится к одному из наиболее часто встречающихся распределений случайных величин. Отчасти это связано с тем, что распределение суммы большого числа независимых случайных величин, обладающих различными законами распределений, часто встречающееся на практике, приближается к нормальному распределению. В этом случае ПРВ и функция распределения имеют вид

,

плотность распределения вероятностей представляет собой функцию текущего значения случайной величины , выражающую вероятность попадания конкретного значения

случайной величины в малый интервал ее возможных значений , примыкающий к , т.е.

- Интеграл вероятностей​(erf ф-я ошибок) = ф-я​Лапласа

2. Оптимальный прием сигналов на фоне помех. Отношение сигнал /шум на входе и выходе оптимального фильтра. Выигрыш оптимального фильтра в отношении сигнал/шум.

Так как пиковое значение выходного сигнала

где 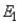-полная энергия сигнала, а мощность шума на выходе

то отношение пика мощности сигнала к мощности выходного шума равно .

Таким образом, отношение сигнал-шум на выходе оптимального фильтра зависит от энергии сигнала на входе и не зависит от его формы, причем в этом случае обеспечивается максимально возможное отношение сигнал-шум, и следовательно, максимально возможная вероятность правильного обнаружения этого сигнала при заданном уровне вероятности ложной тревоги.

Если на входе приемника действует не белый шум, а шум, имеющий неравномерную спектральную плотность мощности, то оптимальный фильтр строится в виде последовательно соединенных двух линейных фильтров (см. рис.7).

Рис. 7 Первый фильтр выбирается таким образом, чтобы шум на его выходе стал белым, т.е. если на входе шум

описывается характеристикой (спектральной плотностью)​, то на выходе фильтра должно выполняться на всех частотах. Следовательно:

, H(w) - ​передаточн характеристики фильтра Для сигнала на выходе первого фильтра будем иметь

Характеристика второго фильтра должны быть согласована с сигналом , т.е.

Частотная характеристика цепочки определяется выражением

Таким образом, такой оптимальный фильтр ослабляет те участки спектра входного колебания, которые соответствуют наиболее интенсивным спектральным составляющим шума.

Отношение сигнал-шум здесь составляет

Выигрыш в отношении сигнал-шум при оптимальной фильтрации численно равен базе входного сигнала, с которым согласован фильтр.

Как известно все сигналы делятся на две группы, в зависимости от величины базы:

-простые Тс [Δfs вх]≈1,

-сложные Тс [Δfs вх]>>1.

Таким образом выигрыш в отношении сигнал-шум получается только для сложных сигналов.

Для простых сигналов выигрыша нет, но нет и проигрыша, который получается при не оптимальном фильтре.

Экзаменационный билет №22

1. Блочный код Хэмминга (7,4). Принцип систематического кодирования. Порядок формирования проверочной матрицы этого систематического кода. Структура порождающей матрица блочного кода в канонической форме.

​Блочный код хэмминга -​Выпишем все различные ненулевые -разрядные двоичные числа как столбцы в возрастающем порядке и используем полученную матрицу в качестве ​проверочной​для

линейного кода. Подобная матрица имеет размер . ,​(m разность параметров кода Хэмминга 7 - 4)

Полученный код называется кодом Хэмминга длины .

Так как число строк проверочной матрицы равно числу проверочных символов, код Хэмминга имеет информационных символов,

т.е. является линейным кодом.

Принцип? ​систематические коды образуют большую группу из блочных, разделимых кодов (в которых все символы слова можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате ​линейных операций​над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.

2. Модели непрерывных каналов с аддитивным шумом: с постоянными параметрами, с неопределенной фазой, с общими и частотно-селективными замираниями.

Канал с аддитивным гауссовским шумом:

n(t) ― случайная аддитивная помеха гауссовский белый (квазибелый) шум с нулевым средним значением и односторонней спектральной плотностью G0(f) = N0

u(t) ― входной сигнал

µ— известные постоянный коэффициент передачи канала τ —время запаздывания сигнала дискретный канал связи

С постоянными параметрами:

С неопределенной фазой:

— сопряженный канал, получаемый посредством преобразования Гильберта от u(t)

Ө = w​τ— случайная фаза, которая, как правило, распределена равномерно на интервале от ​0

0​

до ​2П

Модель канала применяется при случайных колебаниях фазы сигнала, которые вызываются небольшими изменениями протяженности канала, свойств среды, через которую проходит сигнал, а также нестабильностью опорных (задающих) генераторов в передатчиках и приемниках.

С общими и частотно-селективными замираниями:

Общие замирания имеют место, если ширина полосы частот сигнала существенно меньше

интервала корреляции передаточной функции канала по частоте, а

длительность , причем – интервал корреляции функции по времени. Если условие не выполняется, имеют место частотно-селективные замирания, а при невыполнении условия – временные селективные замирания. При одновременном невыполнении условий и имеют место

временные и частотно-селективные замирания. В зависимости от величины отношений и

можно различать медленные и быстрые

селективные замирания.

Экзаменационный билет №23

1. Блочный код Хэмминга (7,4). Структура проверочной матрицы для систематического кода. Принцип кодирования с использованием проверочной матрицы.

Блочный код Хэмминга (7,4):

(n,k)-код: на k входных битов получаем n выходных, то есть вносится n-k=r избыточных (проверочных) битов.

Выпишем все различные ненулевые-разрядные двоичные числа как столбцы в возрастающем порядке и используем полученную матрицу в качестве ​проверочной​для линейного кода. Подобная матрица имеет размер m x (2^m) - 1.

Полученный код называется кодом Хэмминга длины n = (2^m) - 1.

Так как число строк проверочной матрицы равно числу проверочных символов, код Хэмминга имеет k = n - m = (2^m) - m - 1 информационных символов, т.е. является (2^m - 1, 2^m - m - 1) линейным кодом.

Принцип кодирования:

Столбцы проверочной матрицы кода Хэмминга (7,4) это числа от 1 до 7 в двоичной записи:

Чтобы получить кодовое слово, необходимо получить порождающую матрицу G, для этого изменим порядок столбцов проверочной матрицы H, явно выделив единичную матрицу m x m.

Теперь получим систематический вид порождающей матрицы с помощью транспонирования:

Теперь легко закодируем информационное слово “a” с помощью порождающей матрицы и получим кодовое слово u по формуле:

u = aG

2. Межсимвольная интерференция, причины возникновения и способы борьбы с ней. Сигнал Найквиста. Модели каналов с межсимвольными искажениями, принцип получения глазковой диаграммы. Анализ канала по глазковой диаграмме.

Особенностью радиосвязи на большие расстояния часто является передача информации в условиях общих замираний и межсимвольной​​интерференции​.

Межсимвольная интерференция​​(МСИ) это искажения сигнала за счет откликов на более ранние символы, которые могут проявлять себя как помехи. МСИ зависит от вида АЧХ и ФЧХ фильтров в тракте передаче, структуры и параметров кодовой последовательности

7.3.1.