Экзамен / Точно билеты ОТС Удачи(2020)
.pdf
Не зависящее от времени число называют комплексной амплитудой гармонического колебания. С физической точки зрения узкополосные сигналы представляют собой квазигармонические колебания. Следует попытаться так обобщить метод комплексных амплитуд, чтобы иметь возможность
в рамках этого метода описывать сигналы вида
Введем комплексную низкочастотную функцию 
Ну тип А синфазной амплитудой, B квадратурная амплидута
называется комплексной огибающей узкополосного сигнала. Комплексную огибающую, можно представить также в показательной форме: 
Легко непосредственно проверить, что
Полная фазаузкополосного сигнала: 
Выражение для автокорреляционной функции узкополосного сигнала записывается в виде
Где
f0 окрестность несущей частоты
Отметим, что автокорреляционная функция действительного узкополосного сигнала Rх(t) является действительной. Величина Rg(t) представляет автокорреляционную функцию комплексной огибающей сигнала. Соотношение, связывающее Rх(t) с Rg(t) аналогично тому, которое связывает узкополосный действительный сигнал с его комплексной огибающей. Часто целесообразно сначала определить автокорреляционную функцию комплексной огибающей, а затем перейти к корреляционной функции узкополосного сигнала.
Экзаменационный билет №8
1. Корреляционная функция случайного процесса. Определение и основные свойства, формулы расчета для дискретных сигналов, для эргодических непрерывных сигналов.
Корреляционной (ковариационной, автоковариационной, автокорреляционной) функцией случайного процесса X(t) называетсяф-я, которая при каждой паре значений {t1, t2} равна корреляционному моменту соответствующих сечений X(t1) и X(t2):неслучайная функциядвух аргументов K(t1; t2), которая
Свойства:
1.Корреляционная функция при одинаковых значениях аргументов равна дисперсии с.п.
2.Корреляционная функция не меняется относительно замены аргументов, т.е. является
симметрической функцией относительно своих аргументов: 
3. Если к случайному процессу прибавить неслучайную функцию, то корреляционная функция
не меняется, т.е. если 
, то 
. Другими словами является периодической функцией относительно любой неслучайной функции.
4.Модуль корреляционной функции не превосходит произведения с.к.о., т.е.
5.При умножении с.п.X(t) на неслучайный множитель 
её корреляционная функция умножится на произведение f(t1)*f(t2), т.е., если 
, то 
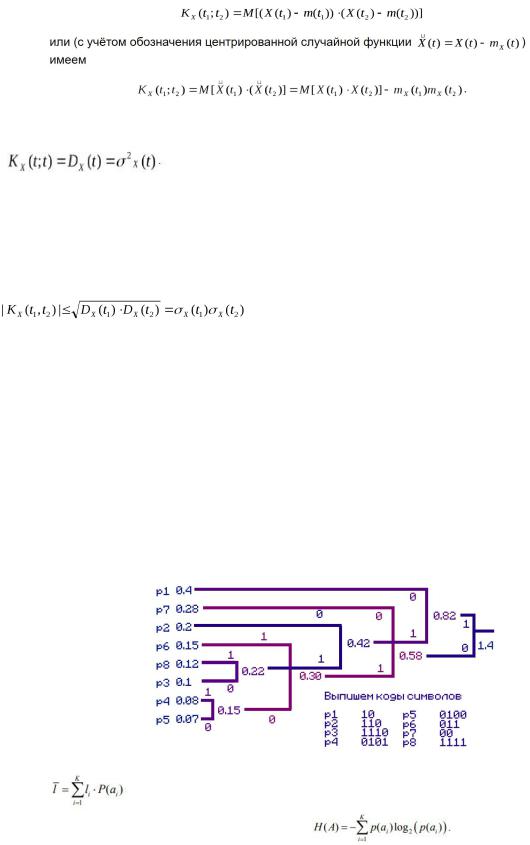
2.Построить дерево эффективного кодирования источника кодом Хаффмена, если вероятности передаваемых символов р1=0.4; р2=0.2; р3=0.1; р4=0,08; р5=0,07; р6=0.15; р7=0.28; р8=0.12. Определить энтропию источника и среднее число бит кода на одно сообщение.
Шаг 1 Упорядочим вероятности передаваемых символов в порядке невозрастания (тупо убывания вот он ах...)
p1 =0.4 ; р7=0.28 ; р2=0.2; р6=0.15; р8=0.12 ; р3=0.1; р4=0,08; р5=0,07.
Шаг 2 Берем два элемента с наименьшими вероятностями и объединяем их (складываем вероятности) наименьшему элементу сопоставляем “0”, наибольшему “1”
p1 =0.4 ; р7=0.28 ; р2=0.2; р6=0.15; р8=0.12 ; р3=0.1; р54=0,15;
Шаг 3 Рассматриваем новую последовательность и повторяем Шаг 2 до тех пор пока не останется один “корень”
p1 =0.4 ; р7=0.28 ; р2=0.2; р6=0.15; р38=0.22 ; р54=0,15;
Определим среднее число бит(цену кодирования: средняя длину кодового слова L)
=2*(0.4+0.28)+3*(0.2+0.15)+4*(0.1+0.08+0.07+0.12)= 3.89 [бит]
Определим энтропию источника по формуле: H(A)=0.528771+0.51422+0.464386+0.410545+0.367067+0.332193+0.291508+0.268555=3.177245[бит]
Экзаменационный билет №9
1. Определение количества информации по Шеннону. Энтропия источника случайных сообщений. Свойства энтропии. Энтропия двоичного источника.
Определение количества информации по Шеннону
Американский инженер-связист Клод Шеннон предложил ввести меру количества информации с помощью статистической формулы энтропии:
,где вероятность Wiпоявления состояния i, Iколичество информации
Энтропия источника случайных сообщений.
Энтропия случайного источника(англ. Shannon entropy) — функция от вероятностей исходов
(оператор объединения) характеризующая количество информации, приходящейся на одно сообщение источника.
Свойства энтропии.
Энтропия двоичного источника. Сделал так-же, как в 11
Случай независимых равновероятных символов
Вероятности: P(a1)=P(a2)=P=0.5 , условные вероятности равны нулю. Энтропия такого источника максимальна:
Hmax=-0.5 * log(0.5)- 0.5 * log(0.5) = log(2) = 1 бит/символ
Таким образом, 1 бит - это максимальное среднее количество информации, которое может переносить один символ источника двоичных сообщений.
Случай независимых неравновероятных символов
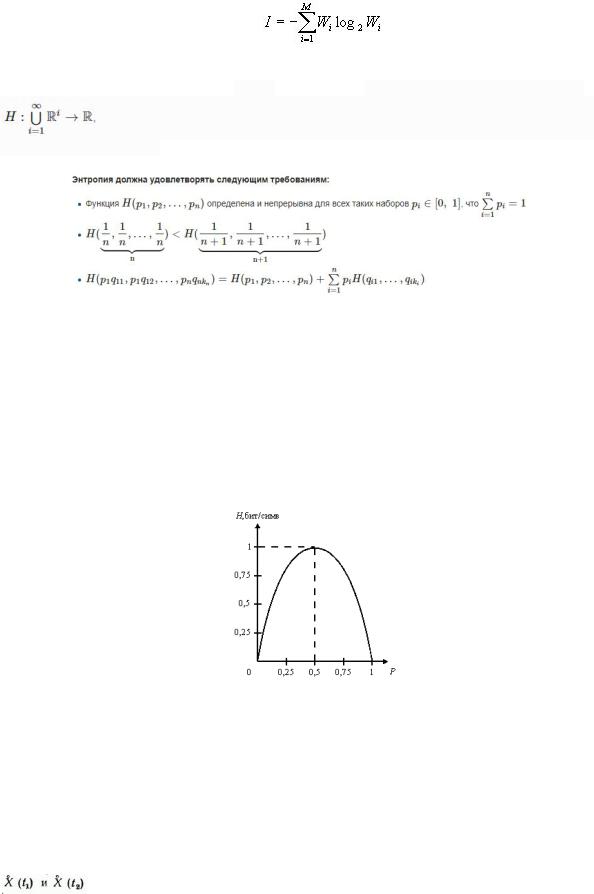
Вероятности: P(a1)=P ; P(a2)=1-P условные вероятности равны нулю. Энтропия такого источника равна: H(P)=-P * log(P) - (1-P) * log(1-P)
Эта зависимость показана ниже на рисунке. Максимум энтропии достигается при P=0.5. Поскольку H(p)< Hmax при P!=0.5, то производительность такого источника меньше максимальной.
Рис. Энтропия двоичного источника сообщений с неравновероятными символами
Случай коррелированных равновероятных символов При некоррелированных равновероятных символах двоичного источника энтропия равна 1
бит/симв. Следовательно, наличие статистических связей между символами приводит к уменьшению энтропии и увеличению избыточности источника.
2. Корреляционная функция стационарного эргодического случайного сигнала. Формула расчета и физический смысл интервала корреляции.
Корреляционная функция стационарного эргодического случайного сигнала.
Корреляционной функцией случайного процесса X(t) называют неслучайную функцию двух аргументов Rx(t1,t2) которая для каждой пары произвольно выбранных значений аргументов (моментов времени) t1 и t2 равна математическому ожиданию произведения двух случайных величин
соответствующих сечений случайного процесса:
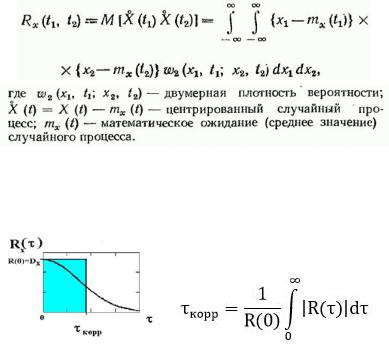
Формула расчета и физический смысл интервала корреляции.
"интервал корреляции" или "время корреляции", под которыми понимается величина временного сдвига, при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента.
Тау - интервал времени; Знак модуля введен для учета случаев, когда R(тау) принимает отрицательные значения
Основание прямоугольника называется интервалом корреляции. На этом интервале можно предсказать случайный сигнал (линейный тренд).
Экзаменационный билет №10
1. Основы спектрально-корреляционной теории случайных сигналов. Понятие спектральной плотности мощности случайного сигнала. Теорема Винера-Хинчина.
Основы спектрально-корреляционной теории случайных сигналов.
Рассмотрим стационарный случайный процесс с нулевым математическим ожиданием: Отдельно взятая реализация этого процесса есть детерминированная функция, которую можно представить в виде,
обратного преобразования Фурье 
с некоторой детерминированной спектральной плотностью. Усредним мгновенные значения сигналов по ансамблю реализаций:
Итак, случайная спектральная плотность отдельных реализаций стационарного случайного процесса должна иметь нулевое математическое ожидание на всех частотах. Теперь нужно определить, при каких условиях функция корреляции зависит лишь от сдвига между сечениями. Воспользуемся тем, что сигнал x(t) вещественный, так что справедливо равенство
Для того чтобы функция не зависела от времени t, необходимо потребовать выполнения следующей пропорциональности:
Таким образом, случайная спектральная плотность стационарного процесса имеет специфическую структуру: ее значения, отвечающие любым двум несовпадающим частотам, некоррелированы между собой. В то же время средний квадрат (дисперсия) случайной спектральной плотности неограниченно велик при любых частотах.
Понятие спектральной плотности мощности случайного сигнала.
Функция Wx(t), играющая фундаментальную роль в теории стационарных случайных процессов, называется спектральной плотностью мощности процесса X(t).
Функции корреляции и спектр мощности стационарного случайного процесса связаны между собой преобразованием Фурье. Поэтому
Теорема Винера-Хинчина.
Автокорреляционную функцию Bx(t) можно представить следующим образом
Но это есть обратное преобразование Фурье, связывающее АКФ случайного процесса с его энергетическим спектром. Очевидно, если существует обратное преобразование, значит, существует и прямое преобразование Фурье
, связывающее энергетический спектр с АКФ. Таким образом, АКФ случайного процесса и его энергетический спектр связаны между собой парой преобразований Фурье. Впервые эта связь была установлена советским математиком А. Хинчиным и независимо от него американским ученым Н. Винером. Поэтому соотношения и носят название теоремы Винера–Хинчина. 2. Принцип помехоустойчивого кодирование канала. Классификация канальных кодов. Отличие блокового кода от сверточного.Обозначение и параметры помехоустойчивых кодов. Кодовое расстояние и его связь с исправляющей и обнаруживающей способностью кода.
Принцип помехоустойчивого кодирования канала.
Для уменьшения количества ошибок, возникающих при передаче информации по каналу с помехами, может быть использовано кодирование в канале, или помехоустойчивое кодирование.
Кодирование с исправлением ошибок представляет собой метод обработки сообщений, предназначенный для повышения надежности передачи по цифровым каналам.
Свойства методов кодирования:
●Количество символов в кодовой последовательности Y всегда больше, чем необходимо для однозначного представления любого сообщения λi из алфавита.
●Свойство усреднения, означающее, что избыточные символы зависят от нескольких
информационных символов, то есть информация, содержащаяся в кодовой последовательности X, перераспределяется также и на избыточные символы.
Существует два больших класса корректирующих кодов – блочные и сверточные.
Определяющее различие между этими кодами состоит в отсутствии или наличии памяти кодера. k-разрядным двоичным словом можно представить 2kвозможных значений из алфавита источника, им соответствует 2kкодовых слов на выходе кодера. Такое множество 2kкодовых слов называется
блочным кодом.
Классификация кодов //А ОТЛИЧИЯ БЛОЧНЫХ ДЕ
Канальные коды можно классифицировать на основе ряда признаков. Первый из них – объем алфавита, согласно которому коды разделяются на двоичные, троичные и т. п.
Другой классификационный признак отражает способ преобразования потока данных (сообщений)
источника в поток кодовых символов. В этом плане коды можно разделить на блоковые и решетчатые (древовидные).В блоковых кодах k битов данных преобразуются в кодовое слово длины n, проверочные символы которого защищают только «свои» k битов данных. В решетчатых (в частности сверточных) кодах текущая группа проверочных символов защищает несколько смежных блоков данных.
В зависимости от явного присутствия битов данных в кодовых словах различают систематические и несистематические коды. Блоковый код из рассмотренного выше примера – систематический, так как первые два символа в любом его слове – «чистые» биты сообщения.
Наконец, название кода часто содержит определение алгоритма построения или имя первооткрывателя: (линейный, циклический, турбокоды, с низкой плотностью проверок на четность, Хэмминга, Голея, Рида-Соломона, БЧХ, и пр.).
Помехоустойчивые (корректирующие) коды классифицируются:
1.По основанию кода m— объему кодового алфавита
2.Блочные и непрерывные
Если длина всех комбинаций блочного кода одинакова - код называют равномерным, в противном случае код является неравномерным
1.Равномерный телеграфный код МТК-2
2.Неравномерные коды Морзе, Хаффмена, Шеннона-Фано
Помехоустойчивый код характеризуют следующими параметрами:
1.Основание кода q – число элементарных символов, выбранных для передачи сообщений.
Например, для двоичного и троичного кода q={0;1}, q={-1;0;1}. 2 3
2.Длина кода n – число символов, выбранных для передачи сообщений.
3.Число информационных позиций в коде, выбранных для передачи данных – k.
4.Число проверочных (контрольных) позиций в коде – l=n-k.
5.Кобщ=2^n – общее количество кодовых последовательностей,
Кразр=2^k – количество разрешенных кодовых последовательностей,
Кзапр=2^1 – количество запрещенных кодовых последовательностей.
6.Скорость передачи кода R=k/n характеризует качество кода.
7.Относительная избыточность кода r=(n-k)/n*100%=(1-R)*100%
Абсолютная избыточность кода l=n-k
8.Вес кодовой последовательности w – количество ненулевых значений позиций кодовой комбинации F(x). Например, F(x)=011101101 Þ w=6 двоичных символов.
9.Кодовое расстояние кода d характеризует возможности кода по контролю ошибок, равно количеству несовпадений в кодовых последовательностях. F1(x)=0111011101
Å |
F2(x)=1011010010 |
|
|
d =11 |
1111=6 |
10. Кратность контролируемой ошибки t (tобн или t_испр). |
|
|
Вероятность ошибки декодирования
Скорость кода
R = logM/nlogm, если m = 2, то R = k/n
Если R <= 1, то код избыточный; если R = 1 - код примитивный
Экзаменационный билет №11
1. Количественное измерение информации. Энтропия дискретного источника и ее свойства. Энтропия двоичного источника.
Ряд задач теории информации относится к определению объема запоминающих устройств, предназначенных для хранения информации. Для решения таких задач нужно научиться измерять количественно объем информации, пропускную способность линии связи и их чувствительность к помехам. Т.О., теория информации представляет собой математическую теорию, посвященную измерению количества информации, преобразованию информации, передаче информации по линиям связи, изучению методов построения различных кодов, и пр.
Энтропия дискретного источника и ее свойства.
На практике встречаются системы, состояния которых непрерывно переходят одно в другое. Для таких систем распределение вероятностей характеризуется плотностью. Такие системы будем называть непрерывными системами.
Рассмотрим систему X, определяемую непрерывной случайной величиной X с плотностью распределения f(x).
Установим некоторый отрезок ∆x, в пределах которого состояния системы X будем считать неразличимыми, т.е. сведем непрерывную систему к дискретной. Это равносильно замене непрерывной кривой на ступенчатую. При этом каждый участок ∆x заменяется одной точкой-представителем xi .
Определим приближенно энтропию системы X рассматриваемой с точностью до дельта x
Свойства:
1)Энтропия — неотрицательное вещественное число. Н(A) ≥ 0 Прямое следствие того,
что 0≤ pi≤ 1,i=1,...,N и свойств функции |
. |
2)Энтропия равна 0, если с вероятностью, равной единице, всегда выбирается один и тот
же символ.
3)Энтропия максимальна, если все символы источника сообщений появляются независимо и равновероятно.
;H - энтропия, p(a) вероятность символа.
4)Энтропия аддитивна (энтропия нескольких независимых источников равна сумме энтропий этих источников)
Энтропия двоичного источника.
Случай независимых равновероятных символов
Вероятности: P(a1)=P(a2)=P=0.5 , условные вероятности равны нулю. Энтропия такого источника максимальна:
Hmax=-0.5 * log(0.5)- 0.5 * log(0.5) = log(2) = 1 бит/символ
Таким образом, 1 бит - это максимальное среднее (ANAL) - количество информации, которое может переносить один символ источника двоичных сообщений.
Случай независимых неравновероятных символов
Вероятности: P(a1)=P ; P(a2)=1-P условные вероятности равны нулю. Энтропия такого источника равна: H(P)=-P * log(P) - (1-P) * log(1-P)
Эта зависимость показана ниже на рисунке. Максимум энтропии достигается при P=0.5. Поскольку H(p)< Hmax при P!=0.5, то производительность такого источника меньше максимальной.
Рис. Энтропия двоичного источника сообщений с неравновероятными символами
Случай коррелированных равновероятных символов
Вероятности: P(a1)=P(a2)=P=0.5 , условные вероятности равны отличны от нуля:
Условная энтропия с учетом соотношения равна:
Где где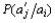 
- условная вероятность появления символа 
после символа 
Например, если 
, то
При некоррелированных равновероятных символах двоичного источника энтропия равна 1 бит/симв. Следовательно, наличие статистических связей между символами приводит к уменьшению энтропии и увеличению избыточности источника.
2. Дисперсия случайного сигнала. Определение, формулы расчета для дискретных и непрерывных сигналов, физический смысл дисперсии, единицы измерения.
Дисперсия случайного сигнала.
Дисперсия– второй центральный момент плотности распределения вероятностей; центральный момент второго порядка.Определение, формулы расчета для дискретных и непрерывных сигналов,
физический смысл дисперсии, единицы измерения.
Физический смысл:дисперсии заключается в том, что она является средней мощностью флуктуаций(любое случайное отклонение какой-либо величины) случайного сигнала,
воздействующего на сопротивление в 1 ОМ.
Экзаменационный билет №12
1. Понятие корреляции случайного сигнала. Определение, формулы расчета для дискретных, непрерывных и эргодических сигналов. Особенности АКФ эргодического сигнала. Физический смысл автокорреляционной функции случайного сигнала.
Корреляционной (ковариационной, автоковариационной, автокорреляционной) функцией случайного процесса X(t) называетсянеслучайная функциядвух аргументов K(t1; t2), которая при каждой паре значений {t1, t2} равна корреляционному моменту соответствующих сечений X(t1) и X(t2):
Свойства:
1.Корреляционная функция при одинаковых значениях аргументов равна дисперсии с.п.
2.Корреляционная функция не меняется относительно замены аргументов, т.е. является
симметричной функцией относительно своих аргументов: 
3. Если к случайному процессу прибавить неслучайную функцию, то корреляционная функция
не меняется, т.е. если 
, то 
. Другими словами является периодической функцией относительно любой неслучайной функции.
4.Модуль корреляционной функции не превосходит произведения ср.кв.о., т.е.
5.При умножении с.п.X(t) на неслучайный множитель 
её корреляционная функция умножится на
произведение f(t1)*f(t2), т.е., если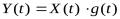 
, то 
Корреляционная функция стационарного эргодического случайного сигнала.
Корреляционной функцией случайного процесса X(t) называют неслучайную функцию двух аргументов Rx(t1,t2) которая для каждой пары произвольно выбранных значений аргументов (моментов времени) t1 и t2 равна математическому ожиданию произведения двух случайных величин
соответствующих сечений случайного процесса:
Формула расчета и физический смысл интервала корреляции.
"интервал корреляции" или "время корреляции", под которыми понимается величина временного сдвига, при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента.
Тау - интервал времени; Знак модуля введен для учета случаев, когда R(тау) принимает отрицательные значения.
Основание прямоугольника называется интервалом корреляции. На этом интервале можно предсказать случайный сигнал (линейный тренд).