Линейное апробование
Это последовательный перебор сегментов
таблицы с некоторым фиксированным
шагом:
адрес=h(x)+ci, где i – номер попытки
разрешить коллизию;
c – константа,
определяющая шаг
перебора.
При шаге, равном единице, происходит последовательный перебор всех
сегментов после текущего.
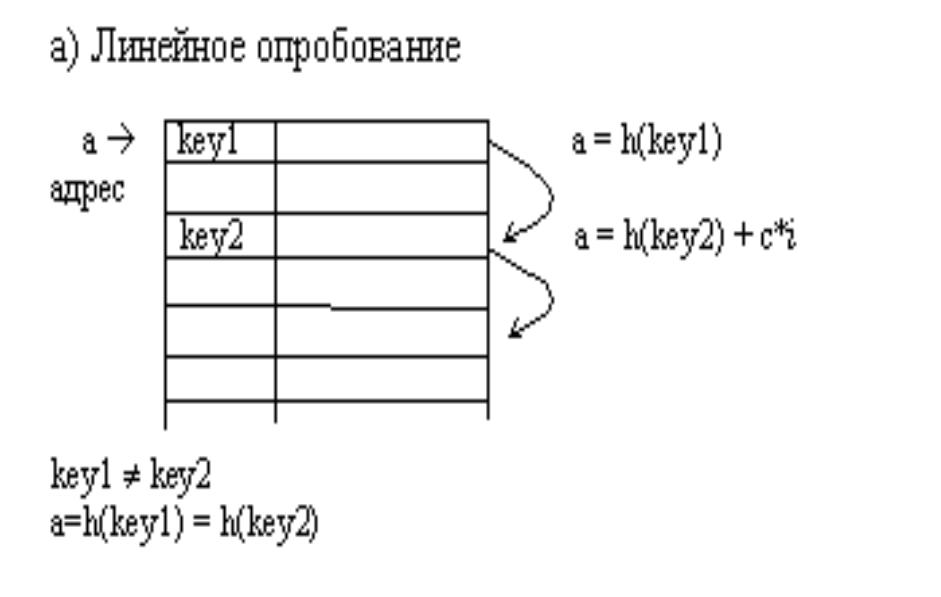
Разрешение коллизий: линейное опробование
Поиск, Linear Probing
•Search for key=20.
–h(20)=20 mod 13 =7.
–Go through rank 8, 9, …, 12, 0.
•Search for key=15
•Example:
–h(x) x mod 13
–Insert keys 18, 41, 22, 44, 59, 32, 31, 73, 12, 20 in this order
–h(15)=15 mod 13=2.
–Go through rank 2, 3 and
return null. |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 |
20 
41 
18 44 59 32 22 31 73 12
0 1 2 3 4 5 6 7 8 9 10 11 12
Квадратичное апробование
отличается от линейного тем, что шаг перебора сегментов нелинейно зависит от номера попытки найти свободный сегмент:
адрес=h(x)+ci+di2, где i – номер попытки разрешить коллизию,
c и d – константы. Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-
синонимов.
Однако, даже относительно небольшое число проб
может быстро привести к выходу за адресное
пространство небольшой таблицы вследствие
квадратичной зависимости адреса от номера
попытки.
Разрешение коллизий: квадратичное опробование
Двойное хэширование
Основана на нелинейной адресации, достигаемой за счет
суммирования значений основной и дополнительной хэш-
функций: адрес=h(x)+ih2(x).
Очевидно, что по мере заполнения хэш-таблицы будут
происходить коллизии, и в результате их разрешения очередной адрес может выйти за пределы адресного пространства таблицы.
Чтобы это явление происходило реже, можно пойти на увеличение длины таблицы по сравнению с диапазоном
адресов, выдаваемым хэш-функцией. С одной стороны, это
приведет к сокращению числа коллизий и ускорению работы с хэш-таблицей, а с другой – к нерациональному расходованию памяти.
Даже при увеличении длины таблицы в два раза по сравнению с областью значений хэш-функции нет гарантии
того, что в результате коллизий адрес не превысит
длину таблицы. При этом в начальной части таблицы
может оставаться достаточно свободных сегментов.
Поэтому на практике используют циклический переход к началу таблицы.
Разрешение коллизий: двойное хеширование
Обработка Коллизий
Метод цепочек
Каждая ячейка в хеш-таблице теперь может содержать список элементов вместо одного элемента
Когда хеш-значения нескольких элементов попадают в одну и ту же ячейку таблицы, они помещаются в список в этой ячейке
Это требует накладных расходов в виде дополнительного списка для каждого слота, который содержит один или более элементов
Метод цепочек
Hash Table contains two items
Data
0
1
2
3
4
2.8
123
John Doe
Jane Doe
3.4
202
Метод цепочек
Insert "Some Guy" with ID = 401
|
|
Data |
|
|
0 |
|
|
1 |
|
Student |
2 |
|
|
|
Name |
Some Guy |
3 |
|
|
|
GPA |
3.5 |
4 |
|
|
ID
401
2.8
123
Jane Doe
John3.Doe4
202