
лекции по физике Родин / ЛЕКЦИЯ № 14 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
.pdf
ЛЕКЦИЯ № 14 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. КВАЗИСТАЦИОНАРНЫЕ ТОКИ.
СВОБОДНЫЕ КОЛЕБАНИЯ В КОНТУРЕ БЕЗ АКТИВНОГО СОПРОТИВЛЕНИЯ.
ЭЛЕКТРОМАГНИТНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.
Среди различных электрических явлений важное место занимают электромагнитные колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически.
Для возбуждения и поддержания электромагнитных колебаний существуют определенные системы, простейшая из которых колебательный контур – цепь, состоящая из последовательно включенных катушки с индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.
Будем считать, что мгновенные значения тока практически одинаковы на всех участках цепи, т.е. ток будет квазистационарным. При этом все изменения тока I во времени настолько медленны, что распространение электромагнитных колебаний происходит мгновенно. Если l – длина цепи, то на ее прохождение электромагнитное возмущение затрачивает время:
cl ,
где с – скорость света, т.е. << T (условие квазистационарности), T – период изменения силы тока I. Это позволит нам использовать формулы, полученные в
статических полях (закон Ома). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим процессы в колебательном контуре. |
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть вначале верхняя обкладка заряжена |
|
|
|
|
K |
|
|
|
|
|
|
K |
|||
положительно «+», а нижняя отрицательно «–». |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При этом вся энергия колебательного контура со- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
средоточена в конденсаторе. Замкнем ключ К. |
|
C L |
|
|
|
C |
|
L |
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
Конденсатор будет разряжаться, и через ка- |
|
|
|
|
|
|
|
||||||||
- |
- - |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
тушку L потечет ток. Электрическая энергия кон- |
|
|
|
|
R |
|
|
|
|
|
|
R |
|||
денсатора начнет превращаться в магнитную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
энергию катушки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wэ=>Wм; ( 2C1 q2 => 12 LI2 ).
Этот процесс закончится, когда конденсатор полностью разрядится. Затем ток, не меняя направления, начнет убывать, но прекратится не сразу, так как его будет поддерживать ЭДС самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Затем ток прекратится, а заряд на конденсаторе станет максимальным. С этого момента конденсатор опять начнет разряжаться, ток потечет в обратном направлении и т.д. – процесс будет повторяться.
При R = 0 в контуре будут совершаться строго периодические колебания. Периодически изменяется заряд на обкладках конденсатора, напряжение на нем и ток через катушку. Колебания сопровождаются взаимным превращением энергии электрического и магнитного полей.
Если R 0 , то будут дополнительные потери на тепло Джоуля-Ленца.
Найдем уравнение электромагнитных колебаний в контуре. |
|
|
|
|
|
|
R |
||
Пусть в контуре содержится внешняя переменная ЭДС ε. |
C |
|
|
|
|
|
|||
1 |
|
|
|
||||||
Выберем положительное направление обхода по контуру по ча- |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
совой стрелке. |
q |
2 |
|
|
|
||||
Ток в цепи (знаки совпадают): |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
I |
dq |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt |
|
|
|
|
|
|
|
|
если I > 0, и dq > 0.
По закону Ома для участка цепи 1RL2
|
|
RI 1 2 S . |
||||||||
В нашем случае S |
L |
dI |
; |
2 1 = |
q |
= UC. |
||||
dt |
|
|
||||||||
|
|
|
|
|
|
C |
||||
Тогда (2) примет вид: |
|
L |
dI |
RI |
q |
. |
||||
|
|
|
||||||||
|
|
|
|
|
dt |
|
|
C |
||
Учитывая, что I dqdt получим уравнение колебательного контура:
L( |
d2q |
) R |
dq |
|
1 |
q , |
dt2 |
|
|
||||
|
|
dt |
|
C |
||
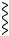 L
L
(1)
(2)
(3)
это линейное дифференциальное, неоднородное уравнение второго порядка.
Найдя с его помощью q(t) , мы можем вычислить U |
|
|
|
q |
– напря- |
|||||||
C |
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
1 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жение на конденсаторе и силу тока I по формуле (1). |
|
|
|
|
|
|||||||
Уравнению (3) можно придать иной вид: |
|
|
|
|
|
|
|
|
||||
q 2 q 2q |
|
, |
|
|
|
|
|
|
(4) |
|||
|
|
|
|
|
||||||||
0 |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где введены обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
2β |
R |
; 2 |
|
1 |
. |
|
|
|
|
(5) |
||
|
|
|
|
|
|
|||||||
|
L |
0 |
|
|
LC |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
Величину 0 называют собственной частотой контура, – коэффициентом затухания.
Если = 0, то колебания называют свободными. При R = 0 колебания будут
незатухающими а при R 0 затухающими.
Из (4), когда = 0 и R = 0, получаем дифференциальное уравнение свобод-
ных гармонических колебаний заряда q в контуре:
q 0q 0 |
(6) |
|
|
2 |
|
Решением этого уравнения является функция: |
|
|
q = qm cos( 0t + ), |
(7) |
|
для тока и напряжения:
I dqdt Im cos( 0 t 2 ) ,
2

UC Cq Umcos( 0 t ) ,
где qm – амплитудное значение заряда на обкладках контура; 0 – собственная частота; – начальная фаза; qm и – определяются начальными условиями. Видно, что при свободных незатухающих колебаниях ток I опережает по фазе напряжение на конденсаторе на /2.
Согласно (5) 2 |
|
1 |
поэтому период свободных незатухающих колебаний: |
|||||
|
||||||||
0 |
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
T |
=> T 2 LC |
(8) |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
(формула Томсона). |
|
|
|
|
|
|
|
|
СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ. ЛОГАРИФМИЧЕСКИЙ ДЕКРЕМЕНТ ЗАТУХАНИЯ.
ДОБРОТНОСТЬ.
Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, расходуется на нагрев. Свободные колебания будут затухающими. Уравнения этих колебаний получают из (4) полагая 0 :
q 2 q 2q 0 , |
(9) |
||
|
|
0 |
|
где – коэффициент затухания. |
|
|
|
Решение этого однородного дифференциального уравнения при β2<ω02(т.е. |
|||
(ω02 – β2)>0) имеет вид: |
|
|
|
q q |
m |
e- t cos( t ) , |
(10) |
|
0 |
|
|
где 
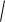 02 2
02 2 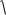
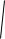 LC1 ( LCR )2 .
LC1 ( LCR )2 .
График функции (10) показан на рис. 1. Видно, что эта функция не периодическая, она определяет затухающие колебания. Величину T = 2 / называют периодом затухающих колебаний:
q |
q e t |
|
|
|
|
|
|
|
T |
|
2 |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
q m |
|
|
|
|
|
|
|
|
2 2 |
|||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q q |
m |
e t |
cos( t ) |
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
0 |
|
|
|
e- t |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Множитель |
q |
m |
в (10) называют ампли- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
тудой затухающих колебаний. Зависимость |
|||||||
|
|
|
|
|
|
|
|
ее от времени показана пунктиром на рис. 1 |
||||||||
qm |
|
|
|
T |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q |
m |
e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ.1. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Зная зависимость q(t), можно найти напряжение на конденсаторе и ток в контуре. Расчет показывает, что при наличии активного сопротивления R ток в контуре опережает по фазе напряжение на конденсаторе более чем на /2.
3
ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ ЗАТУХАНИЕ.
1.Коэффициент затухания и время релаксации промежуток времени,
втечение которого амплитуда колебаний уменьшается в е раз. Нетрудно видеть,
что = 1/ .
2. Логарифмический декремент затухания . Он определяется как нату-
ральный логарифм отношения двух значений амплитуд, взятых через период колебания Т:
ln |
A(t) |
T или = 1/Ne, |
A(t T) |
где А амплитуда соответствующей величины (q, U, I), Ne число колебаний за время , т.е. за время, в течение которого амплитуда колебаний уменьшается в е раз.
3. Добротность Q колебательного контура:
Q N ,e
где логарифмический декремент затухания. Чем меньше затухание, тем боль-
ше Q. При слабом затухании 2 2 |
добротность Q |
1 |
|
|
L |
|
. |
|
|
||||||
0 |
|
R |
|
|
C |
||
|
|
|
|
||||
В заключение отметим, что при 2 02 вместо колебаний будет происхо-
дить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим:
Rкр = 2 
 L / C .
L / C .
ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ. ВЕКТОРНАЯ ДИАГРАММА.
РЕЗОНАНСНЫЕ КРИВЫЕ ДЛЯ НАПРЯЖЕНИЯ И СИЛЫ ТОКА
Рассмотрим случай, когда в контур включена внешняя переменная ЭДС , зависящая от времени по гармоническому закону:
R |
L |
C |
mcos t . |
|
(11) |
||
В данном случае уравнение колебательно- |
|||||||
|
|
|
|||||
|
|
го контура записывается как: |
|
||||
U R |
U L |
U C |
L dI |
RI q |
mcos t , |
(12) |
|
|
|
|
dt |
C |
|
|
|
|
|
или |
q 2 q 2q m cos t . |
(13) |
|||
|
|
|
|
0 |
L |
|
|
|
|
|
|
|
|
||
Решение этого уравнения представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения. Нас интересуют установившиеся колебания, т.е. частное решение этого уравнения (общее решение однородного уравнения равно нулю)
q qmcos( t ) , |
(14) |
где qm – амплитуда заряда на конденсаторе; – разность фаз между колебаниями заряда и внешней ЭДС .
4

Расчеты показывают, что qm и определяются только свойствами самого контура и вынуждающей ЭДС , причем оказывается, что >0, поэтому q всегда отстает по фазе от .
Из последнего уравнения дифференцированием по t получаем:
|
I q |
sin( t ) q |
m |
cos( t ) |
(15) |
|
m |
|
2 |
|
|
|
I Im cos( t ) , |
|
|
||
или |
|
|
(16) |
||
где Im амплитуда тока; сдвиг по фазе между током и внешней ЭДС : |
|
||||
|
Im = qm, |
|
(17) |
||
|
2 |
||||
|
Представим исходное уравнение (12) в виде: |
|
|||
|
UL + UR + UС = mcos t, |
(18) |
|||
где слева записана сумма напряжений на индуктивности L, сопротивлении R и емкости С. Таким образом, мы видим, что сумма этих напряжений равна в каждый момент внешней ЭДС . Учитывая соотношения (17), запишем:
|
|
|
|
|
UR = RI = RImcos( t ), |
|
|
|
(19) |
||||||||||
|
|
|
|
|
UC |
= |
q |
|
qm |
cos( t ) |
Im |
cos( t ) , |
(20) |
||||||
|
|
|
|
|
|
|
|
C |
|||||||||||
|
|
|
|
|
|
|
C |
C |
0 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
UL |
= L |
dI |
|
LIm sin( t ) LIm cos( t ) . |
(21) |
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из последних трех формул видно, что: |
||
LI |
m |
|
|
|
|
|
|
|
|
|
|
|
|
UR находится в фазе с током I; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UC отстает по фазе от I на /2; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
m |
|
|
|
( L |
)Im |
UL опережает I на /2. |
|
|||||||
|
|
|
|
|
|
|
|
C |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все это можно наглядно представить с |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
помощью векторной диаграммы, изобразив |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
амплитуды напряжений: |
|
|||
|
Im |
|
|
|
RI m |
|
Îñü |
òîêà |
|
|
URm = RIm, UCm = Im/ C, ULm = LIm |
||||||||
|
|
|
|
и их векторную сумму, равную согласно (18) |
|||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Ðèñ.2 |
|
|
|
|
|
|
|
|
|
вектору величины m (рис. 2.). |
|
||||||
Из прямоугольного треугольника этой диаграммы легко получить следующие выражения для Im и :
Im |
|
|
m |
|
, |
(22) |
|
|
|
|
|
||||
R 2 |
( L 1/ C)2 |
||||||
|
|
|
|
|
|||
tg |
L 1/ C . |
|
|
(23) |
|||
|
|
|
R |
|
|
|
|
Заметим в заключение, что полученная нами векторная диаграмма оказывается весьма полезной при решении многих конкретных вопросов. Она позволяет наглядно, легко и быстро анализировать различные ситуации.
5
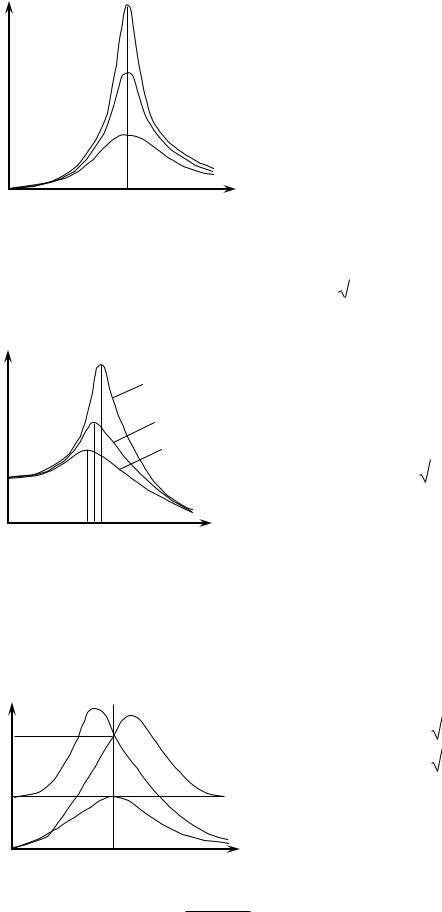
Im
0 |
0 |
|
|
Ðèñ. 3 |
|
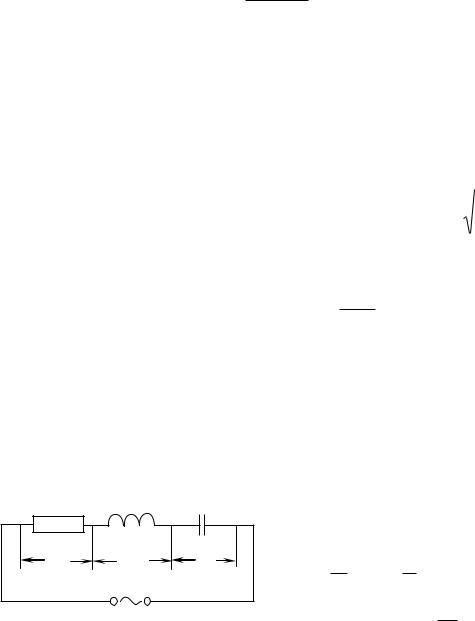
Рассмотрим резонансные кривые, т.е. графики зависимостей от частоты внешней ЭДС амплитуд следующих величин: тока I, заряда q на конденсаторе и напряжений UR, UC и UL, определяемых формулами (19) (21).
Резонансные кривые для силы тока Im( ) показаны на рис. 3. Как видно из выражения (22), амплитуда силы тока имеет максимальное значение при L 1/ С = 0.
Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура:
|
|
|
|
|
Iрез = 0 = 1/ LC . |
|
|
|
|
Максимум при резонансе оказывается тем выше и острее, чем меньше ко- |
|||||
эффициент затухания = R/2L. |
|
|
|
||||
q m |
|
|
|
Резонансные кривые для заряда на конден- |
|||
|
1 |
|
саторе qm( ) показаны на рис. 4. (резонансные |
||||
|
|
|
|
||||
|
|
|
2 |
|
кривые для напряжения UCm на конденсаторе име- |
||
|
|
|
|
ют такой же вид). Максимум амплитуды заряда |
|||
|
|
|
3 |
|
достигается при резонансной частоте: |
||
|
|
|
|
|
|
|
|
q |
0 |
|
|
|
qрез = |
02 2 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которая по мере уменьшения все больше при- |
||
|
|
|
|
|
ближается к 0. |
|
|
|
|
|
|
|
|
||
|
0 |
0 |
|
|
|||
|
1 < 2 < 3, т.е. чем меньше R. |
||||||
|
|
Ðèñ. 4 |
|
|
|||
|
|
|
|
|
|
|
|
Теперь посмотрим, как перераспределяются амплитуды напряжений UR, UC и UL в зависимости от частоты внешней ЭДС.
Эта картина изображена на рис. 5. Резонансные частоты для UR, UC и UL определяются следующими формулами:
|
|
|
|
|
Rрез = 0 |
||||||
|
|
|
|
|
Cрез = 0 |
|
|
|
|
|
|
Q m |
|
|
|
|
|
1 2( / )2 |
|||||
|
|
ULm |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
Lрез = 0 |
|
|
|
||||
|
UCm |
|
1 2( / )2 |
||||||||
|
|
|
|
|
|
0 |
|
|
|||
m |
|
|
|
Чем меньше , тем ближе резонансные частоты |
|||||||
|
|
|
всех величин к значению 0. |
||||||||
|
|
|
|
||||||||
|
|
URm |
|
Из |
векторной |
диаграммы наблюдается |
|||||
|
|
|
|
явление резонанса, например Im (qm ) , при сов- |
|||||||
0 |
0 |
||||||||||
падении собственной частоты контура и часто- |
|||||||||||
|
|
|
|
||||||||
Ðèñ. 5 |
ты внешней вынуждающей силы ЭДС. |
|
Для qm( ) => ðåç 
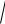 02 2 2 и т.д.
02 2 2 и т.д.
6
Явление резонанса в нашем случае это возбуждение сильных колебаний при частоте внешней ЭДС или напряжения, равной или близкой к собственной частоте колебательного контура. Резонанс используют для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т.е. изменением С и L колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.
С явлением резонанса связана и опасность: внешняя ЭДС или напряжение могут быть малы, однако при этом напряжения на отдельных элементах кон-
тура (на емкости или индуктивности) могут достигать опасного для жизни значения. Об этом необходимо всегда помнить!
7
