лекции по физике Родин / LEKTsIYa__04_ELEKTRIChESKIJ_DIPOL

ЛЕКЦИЯ № 4

ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ.

ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ДИПОЛЯ.

Электрический диполь – это система двух одинаковых по модулю разноимённых точечных зарядов +q и –q, находящихся на расстоянии l друг от друга. Прямая, проходящая через оба заряда, называется осью диполя. Когда говорят о поле диполя, предполагают сам диполь точечным, то есть считают расстояние r от диполя до интересующей точки М значительно больше l: r >> l.

Поле диполя обладает осевой симметрией, и картина поля в любой плоскости, походящей через ось диполя, одна и та же, и вектор лежит в этой плоскости. Найдём потенциал поля диполя, а затем его напряжённость.

Согласно выражению для потенциала поля точечного заряда в точке М потенциал определяется как:

. (1)

Так как r >> l, то из рисунка видно, что и произведение r_r₊ = r², где r – расстояние от точки M до диполя (он точечный). С учётом этого:

, (2)

то есть потенциал определяется q и l.

Величину p = ql называют электрическим моментом диполя, или дипольным моментом. Этой величине сопоставляют вектор, направленный по оси диполя от отрицательного заряда к положительному.

(3)

где q > 0 и вектор направлен в ту же сторону, т. е.

(4)

Для нахождения поля диполя воспользуемся формулой:

(5)

полученной из соотношения: ; записав , где dl =  элементарный путь, E_e  проекция вектора на перемещение . Символ частной производной подчёркивает, что производная потенциала берется по данному направлению.

Вычислим проекции вектора на два взаимно перпендикулярных направления вдоль ортов и :

(6)

.

(Подробнее см. Савельев И.В. Курс физики т.2, §10 стр. 44).

Из рисунка и выражения (6) модуль вектора :

(7)

В частности при  = 0 и  = /2, мы получим выражения для проекций и

и , (8)

т. е. при одном и том же r напряжённость вдвое больше .

СИЛА, ДЕЙСТВУЮЩАЯ НА ДИПОЛЬ.

Поместим диполь во внешнее неоднородное электрическое поле. Пусть E₊ и E_  напряжённости в точках, где расположены положительный и отрицательный заряды диполя.

Тогда результирующая сила , действующая на диполь, равна

Разность  это приращение вектора на отрезке, равном длине диполя l, в направлении вектора . Вследствие малости этого отрезка можно записать:

.

После подстановки этого выражения в формулу для получим, что сила действующая на диполь:

. (9)

Производная  довольно сложная математическая операция, поэтому не будем вдаваться в подробности, а займёмся сутью полученного результата.

В однородном поле , поэтому = 0, т. е. сила действует на диполь только в неоднородном электрическом поле. Направление вектора в общем случае не совпадает ни с вектором , ни с вектором . Совпадает лишь с элементарным приращением , взятым в направлении вектора или .

Если нас интересует проекция на некоторое направление х, то (9) достаточно записать в проекциях на это направление .

П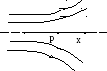усть диполь с моментом расположен вдоль оси симметрии неоднородного поля . Ось х имеет положительное направление. Так как приращение проекции E_х в направлении вектора отрицательно, то F_х<0, а значит вектор направлен влево  в сторону, где напряжённость поля больше.

МОМЕНТ СИЛ, ДЕЙСТВУЮЩИЙ НА ДИПОЛЬ.

Выясним, как ведёт себя диполь во внешнем электрическом поле в своей системе центра масс. Для этого найдём момент внешних сил относительно центра масс диполя (чтобы исключить момент сил инерции).

По определению момента сил: ; , относительно точки C:

,

где и  радиус-векторы зарядов +q и –q относительно точки C. При достаточно малом расстоянии между зарядами диполя и .

Так как. и , то

. (10)

Этот момент сил стремится повернуть диполь так, чтобы его электрический момент установился по направлению поля , такое положение диполя является устойчивым.

ИТАК, в неоднородном электрическом поле:

1. под действием момента сил (10) диполь стремится установиться по полю

;

2. под действием результирующей силы диполь переместится в направлении, где по модулю больше;

3. оба движения будут совершаться одновременно.

ЭНЕРГИЯ ДИПОЛЯ В ПОЛЕ.

Энергия точечного заряда q во внешнем поле

,

где  потенциал поля в точке нахождения заряда q.

Диполь – это система из двух зарядов, поэтому его энергия во внешнем поле:

,

где  потенциал в точке расположения q₊ и q_ с точностью до величины второго порядка малости

,

где  производная потенциала по направлению вектора .

Выражение перепишем как и тогда:

.

Теперь энергию точечного заряда можем представить как скалярное произведение векторов и

.

Из этой формулы следует, что минимальную энергию W_min= pE диполь имеет в положении . При отклонении от этого положения возникает момент внешних сил, возвращающий диполь к положению равновесия.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.

Истинное электрическое поле в любом веществе называют микрополем, потому что оно редко изменяется как в пространстве, так и во времени. Для многих целей достаточно пользоваться усреднённым микрополем по физически бесконечно малому объёму. Это поле называют макрополем. При этом сглаживаются все изменения микрополя на расстоянии порядка атома, и сохраняется плавное изменение макрополя на макроскопических расстояниях.

.

Физически бесконечно малый объём – это объём, содержащий большое число атомов, но имеющий размеры много меньшие, чем те расстояния, на которых макрополе меняется заметно.

При внесении любого проводника в электрическое поле, в этом проводнике происходит смещение положительных и отрицательных зарядов (электронов, ядер), что в свою очередь приводит к частичному разделению этих зарядов.

Пусть имеем нейтральное незаряженное тело (пластинка рис. а).

Мы подносим заряженное тело к нейтральному и оно заряжается (рис. б), т. е. новых зарядов не возникает, а происходит их разделение.

Это явление возникновения не скомпенсированных зарядов разного знака называют электростатической индукцией, а появившиеся заряды – индуцированными зарядами. Эти индуцированные заряды создают дополнительное электрическое поле, которое совместно с внешним полем образует результирующее.

Зная E_внешн и распределение индуцированных зарядов, можно при нахождении результирующего поля не обращать внимание на наличие самого вещества, т. к. его роль уже учтена с помощью индуцированных зарядов.

ПОЛЕ ВНУТРИ ПРОВОДНИКА И НА ЕГО ПОВЕРХНОСТИ.

РАСПРЕДЕЛЕНИЕ ЗАРЯДА В ПРОВОДНИКЕ.

При внесении проводника во внешнее электрическое поле (или сообщении ему некоторого заряда) на заряды в проводнике будет действовать электрическое поле, в результате чего они начнут перемещаться. Отрицательные заряды (электроны) сместятся против поля. Такое перемещение зарядов (ток в течение сотых долей секунды) будет продолжаться до тех пор, пока не установится определённое распределение зарядов, при котором электрическое поле внутри проводника во всех точках обратится в нуль. То есть в статическом случае (неподвижных зарядов) электрическое поле внутри проводника отсутствует ().

Так как в проводнике , то плотность избыточных (нескомпенсированных) зарядов внутри проводника так же равно нулю ( = 0). Это ясно из теоремы Гаусса:

или .

Внутри , т.е. сквозь любую замкнутую поверхность внутри проводника поток Ф = 0, а значит и  = 0, т. е. избыточных зарядов внутри проводника нет.

Избыточные заряды появляются лишь на поверхности проводника с некоторой плотностью , различной в разных точках его поверхности (в поверхностном слое  12 межатомных расстояний). Отсутствие поля внутри проводника означает согласно связи E и  ( = ), что потенциал  в проводнике одинаков во всех его точках.

Таким образом, любой проводник в электростатическом поле представляет собой эквипотенциальную область, и его поверхность является эквипотенциальной.

У поверхности проводника поле направлено по нормали к ней в каждой точке.

Примеры:

1) проводник в виде сферы; 2) плоская металлическая пластина.

ИТАК: 1) Внутри проводника ; а   0;

2) Напряженность у поверхности направлена по нормали E=E_n.

Величина поля у поверхности проводника определяется выражением:

,

что следует из теоремы Гаусса. Линии перпендикулярны поверхности, поэтому возьмём в качестве замкнутой поверхности цилиндрическую поверхность. Поток через эту поверхность будет равен потоку через «наружный» торец (Ф_Sбок и Ф_{Sнижн. осн.} равны нулю). В этом случае теорема Гаусса записывается в виде:

E_nS =  E_n = .

Графически, нейтральный проводник, внесённый в электрическое поле, разрывает часть линий напряжённости: они закончатся на отрицательных индуцированных зарядах и вновь начнутся на положительных зарядах.

Так как в состоянии равновесия внутри проводника (отсутствуют заряды), то создание внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Поле внутри полости равно нулю. Если проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т. е. полость полностью изолирована от влияния внешних электростатических полей. На этом основана электростатическая защита – экранирование тел (измерительных приборов).

Если в полости имеются заряды, то индуцированные на поверхности заряды располагаются так, чтобы скомпенсировать поле внутри полости (∑q = 0) и E = 0, как внутри, так и снаружи. Как бы мы их внутри полости не перемещали, поле снаружи не изменится, т. е. замкнутая проводящая оболочка разделяет всё пространство на внутреннюю и внешнюю части в электрическом отношении не зависящие друг от друга.

6