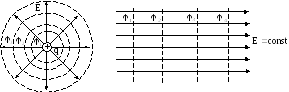лекции по физике Родин / LEKTsIYa__03_TEOREMA_O_TsIRKULYaTsII_VEKTORA_E_POTENTsIAL

ЛЕКЦИЯ № 3

ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА . ПОТЕНЦИАЛ.

Из механики Вы знаете, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а зависит только от положения начальной и конечной точек. Именно таким свойством обладает электростатическое поле  система неподвижных зарядов.

Е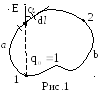сли в качестве пробного заряда переносимого из точки 1 поля в точку 2 выбрать единичный положительный заряд q₀ = 1 (рис.1), то элементарная работа сил поля на перемещении определяется выражением:

dA = = q₀ = , т.к. = q₀

и вся работа сил поля на пути от 1 к 2 определится:

A₁₂ = q₀.

При q₀ = 1 работа A₁₂ определяется интегралом:

(1)

Этот интеграл берётся по некоторой линии (пути) поэтому его называют линейным. Из-за независимости линейного интеграла (1) от формы пути между двумя точками следует, что по произвольному замкнутому пути 1-a-2-b-1 (рис.1) этот интеграл равен нулю. Интеграл (1) по замкнутому пути называют циркуляцией вектора и обозначают .

Величина в случае единичного положительного заряда совпадает с работой кулоновских сил на элементарном перемещении указанного заряда:

dA = =q₀.

Следовательно, физический смысл циркуляции вектора  это работа по перемещению единичного положительного заряда вдоль замкнутой траектории в поле кулоновских сил.

Итак, в любом электростатическом поле циркуляция вектора равна нулю: (2)

Это утверждение называют теоремой о циркуляции вектора .

Можем доказать, что на пути 1-a-2 и 2-b-1 выражение (1) равно нулю.

Поле, обладающее свойством (2) называют потенциальным и, следовательно, любое электростатическое поле является потенциальным.

Теорема о циркуляции позволяет сделать ряд выводов, практически не прибегая к расчётам.

ПРИМЕРЫ: 1. Линии электростатического поля не могут быть замкнутыми,  они начинаются на положительных («+») зарядах и заканчиваются на отрицательных («») зарядах. Если бы линии электростатического поля были замкнуты то, взяв циркуляцию вдоль линии поля, мы получили бы .

2. Не может существовать поле, в котором силовые линии имеют разную плотность (рис.2).

На вертикальных участках и , на горизонтальных участках , т.к. значения разные по модулю на нижнем (реже) и верхнем (гуще) участках.

Мы описывали поле до сих пор с помощью вектора . Существует и другой способ описания поля с помощью потенциала φ. Эти способы однозначно соответствуют друг другу.

Тот факт, что интеграл (1) представляющий собой работу сил поля при перемещении единичного положительного заряда из точки 1 в точку 2 не зависит от формы пути между этими точками, позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат φ(), убыль которой:

φ₁ – φ₂ = (3)

где φ₁ и φ₂ – значения функции φ в точках 1 и 2. Определенная таким образом величина φ() называется потенциалом поля.

Из сопоставления выражения (3) с выражением для работы сил потенциального поля (которое равно убыли потенциальной энергии частицы в поле) можно записать:

A₁₂ = W₁ – W₂,

где W₁ – W₂ есть убыль потенциальной энергии.

Можно сказать, что потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля:

, (4)

где φ – скалярная величина. Единицей потенциала является вольт (В).

Потенциал φ определяется с точностью до произвольной аддитивной постоянной. Для потенциала также справедлив принцип суперпозиции:

 = _i. (5)

Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

У Савельева И.В. определение потенциала даётся исходя из выражения:

A_∞ = q φ. (6)

Потенциал численно равен работе, совершаемой силами поля над положительным единичным зарядом при удалении его из данной точки на бесконечность.

ВЫВОДЫ: Потенциал – это энергетическая характеристика электрического поля, в то время как напряженность электрического поля – силовая характеристика.

ПОТЕНЦИАЛ ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА И СИСТЕМЫ ЗАРЯДОВ.

Выражение (3) содержит не только определение потенциала, но и способ нахождения этой функции. Для этого достаточно вычислить интеграл по любому пути между двумя точками и представить, затем полученный результат в виде убыли некоторой функции, которая и есть φ(r).

Воспользуемся тем, что (3) справедлива и для элементарных перемещений . Тогда элементарная убыль потенциала на этом перемещении:

–dφ = (7)

и, следовательно, можно записать:

φ₂ – φ₁ =.

Таким образом, если известно поле (r), то для нахождения φ нужно представить (путём преобразований) как убыль некоторой функции. Эта функция и есть φ.

Найдём этим способом потенциал поля неподвижного заряда:

, т.к. .

Тогда

,

где  орт радиус вектора проведённого от заряда в данную точку ( = 1).

З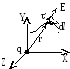апишем ()_r= dr, т.к. проекция вектора на вектор (а значит и на ) равна приращению вектора , т.е. dr.

Следовательно,

.

Величина, стоящая под знаком дифференциал (в круглых скобках) и есть φ(r), а так как аддитивная постоянная const никакой физической роли не играет, то её убирают, и можно записать ( = 1):

 =. (8)

Потенциал уединённого точечного заряда можно ввести и другим способом. Воспользуемся рисунком, на котором представлен перенос единичного заряда из точки 1 в точку 2.

По определению:

φ₁  φ₂=.

В нашем случае:  и dl = dr = r₂  r₁, cos() = 1, поэтому величина .

Подставим это выражение

.

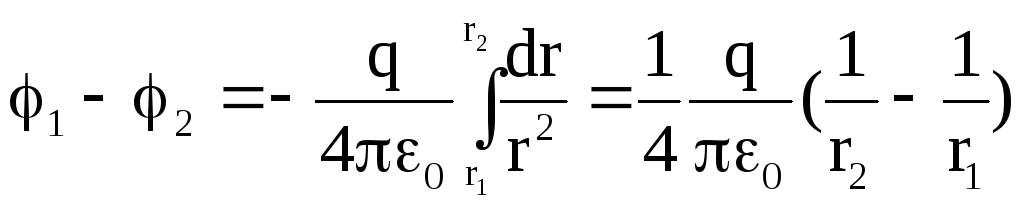Физический смысл имеет разность потенциалов, и можно придать потенциалу в какой-то точке произвольное значение, например, φ₂ = 0 при r₂ = ∞. Тогда потенциал уединённого точечного заряда равен:

φ =.

К такому же результату можем прийти, вычисляя работу силы поля по перемещению заряда на участке (Савельев И.В. Курс физики 1989 г., т.2, § 8).

Для системы неподвижных зарядов, используя принцип суперпозиции, имеем:

, (9)

где r_i  расстояние от точечного заряда q_i до интересующей точки.

Если заряды распределены непрерывно, по всему объёму пространства, то:

. (10)

Если заряды только на поверхности то

. (11)

ДОШЛИ!!!

СВЯЗЬ ПОТЕНЦИАЛА И НАПРЯЖЕННОСТИ

ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

Зная потенциал φ(r) данного электрического поля можно восстановить и само поле (r). Связь между потенциалом φ и напряженностью электрического поля можно установить с помощью уравнения (7).

П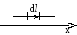усть перемещение параллельно оси X. Тогда , где  орт оси X, dx  приращение координаты X. В этом случае , где E_x  проекция вектора на орт (а не на перемещение ).

Сопоставив последнее выражение с (7) получим:

E_x = , (12)

где символ частной производной подчёркивает, что функцию φ(x,y,z) надо дифференцировать только по x, считая y и z при этом постоянными.

Рассуждая аналогично, можно получить соответственное выражение для проекций E_y и E_z , а определив E_x , E_y и E_z легко найти и сам вектор :

= . (13)

Величина, стоящая в скобках, есть не что иное как градиент потенциала φ (grad φ или ),  произведение символического вектора  на скаляр φ.

В этом случае уравнение (13) можно представить в виде:

= grad φ или = . (14)

Напряжённость поля равна со знаком «» градиенту потенциала.

Знак «» обозначает, что вектор направлен в сторону убывания потенциала.

Для графического изображения потенциала электростатического поля, как и в случае поля тяготения, пользуются понятием эквипотенциальные поверхности (ЭПП)  поверхностями, во всех точках которых потенциал φ имеет одно и то же значение:

φ(x,y,z) = const.

Линии напряженности вектора всегда нормальны к эквипотенциальным поверхностям, да и проекция вектора на любое направление касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это означает, что работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

ВЫВОДЫ:

1) ЭПП расположены перпендикулярно линиям напряжённости ;

2) Вокруг каждого заряда можно провести большое множество ЭПП;

3) ЭПП проводят так, чтобы разности потенциалов между 2-мя соседними поверхностями были одинаковы. Следовательно, густота ЭПП характеризует напряженность электростатического поля, где эти поверхности гуще, там модуль вектора больше.

5