erovenko_va_osnovy_vysshei_matematiki_dlia_filologov

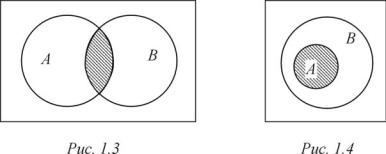
Примером упорядоченного множества является предложение, если под ним понимать совокупность конечного числа слов, расставленных в определенном порядке. Например:

1.Эта юноша молодая.

2.Эта девушка прекрасна.

Определение пересечения множеств. Пересечением двух множеств A и B, обозначается A B, называется множество, которое состоит из всех элементов, принадлежащих каждому из множеств A и B:

def

A B {x : x A è x B}.

Символ «равенства с def» в этой формуле означает «равенство по определению», т.е. то, что стоит слева от этого символа, определяется через то, что стоит справа, а def — это сокращение от латинского слова definito — определение.

Например, если A — «множество студентов 3-го курса филологиче- ского факультета», а B — «множество девушек, которые учатся на филоло-

гическом факультете», то A B — «множество девушек-студенток 3-го курса, которые учатся на филологическом факультете». Если A — «множе-

ство четных чисел», а B — «множество двузначных чисел», то A B — «множество четных двузначных чисел».

Операция пересечения множеств широко применяется в лексикографической практике, в частности, при составлении двуязычных и многоязычных словарей.

Если множества A è B не имеют общих элементов, то их пересечение

пусто, A B = , и в таком случае говорят, что множества A и B не пересекаются. На рис. 1.3 и 1.4 приведены диаграммы Эйлера–Венна для двух

множеств A è B в случаях, когда соответственно A B è A B. Множе-

ñòâó A B на этих рисунках соответствует заштрихованная часть диаграмм.

Операция «пересечение» множеств обладает рядом свойств, напоминающих свойства операции «умножения» чисел. Однако некоторые свой-

32

ства пересечения множеств отличаются от соответствующих свойств умножения.

Åñëè A подмножество множества B, ò. å. A B, òî A B = A (см. рис. 1.4), поскольку общими для множеств A è B будут все элементы множества A и только они. Отметим свойства пересечения справедливые для любых множеств A, B è C:

A B A è A B B.

Кроме того, из включения A B следует включение A C B C. В частности, для любого множества A имеет место равенство A = . Также верно равенство A A = A (идемпотентность пересечения), поэтому нет смысла говорить, например, о «степени» множества в том смысле, в каком говорят о степени числа. Эти свойства отличают операцию пересече- ния множеств от операции умножения чисел и легко проверяются на различных множествах.

Пример. Пусть A — «множество, состоящее из различных букв русского алфавита, входящих в первую строку “Евгения Онегина”», B — «множество, состоящее из различных букв, входящих во вторую строку

этого романа в стихах». Найдем пересечения этих множеств A B. Множество A состоит из 18 различных букв:

A = {М, О, Й, Д, Я, С, А, Ы, Х, Ч, Е, Т, Н, П, Р, В, И, Л}, а множество B состоит из другой совокупности 13 букв:

B = {К, О, Г, Д, А, Н, Е, В, Ш, У, Т, З, М}. Пересечением этих множеств является следующий набор из 8 букв:

A B = {Ì, Î, Ä, À, Å, Ò, Í, Â},

который содержится как во множестве A, так и во множестве B.

Замечание. В предложениях естественного языка возможны относящиеся к подлежащему определения, которые не ограничивают его зна- чения и являются отдельными множествами, задаваемыми характеристическими свойствами.

Например, с помощью имеющихся у нас понятий «подмножество» и «пересечение множеств» запишем на языке теории множеств математиче- скую формулировку предложения: «Онегин, добрый мой приятель, родил-

ся на брегах Невы».

Пусть универсальным множеством будет все множество людей. Обозначим через A — «одноэлементное множество, состоящее из Онегина», B — «множество добрых приятелей автора», C — «множество людей, родивших-

33

ся на брегах Невы». Тогда математической формулой данной строки из «Евгения Онегина» в терминах теории множеств будет включение:

A (B C).

Напомним, что в пересечении множеств использована связка « è ».

Определение объединения множеств. Объединением двух множеств A и B, обозначается A B, называется множество, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств A и B:

def

A B {x : x A èëè x B}.

Например, если A — «множество всех девушек, которые учатся на филологическом факультете», а B — «множество всех юношей, которые учатся на том же факультете», то A B — «множество всех студентов филологического факультета». Если A — «множество всех нечетных натуральных чисел», а B — «множество всех четных натуральных чисел», то A B — «множество всех натуральных чисел».

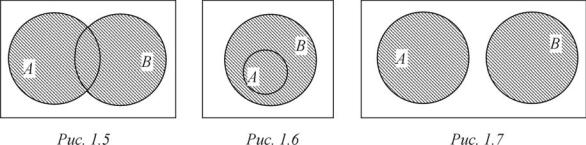
В рассмотренных примерах объединяемые множества не имели общих элементов, т. е. их пересечение было пусто. Если какой-нибудь элемент входит в множество A и в множество B, ò. å. A B , òî в их объединение A B он входит один раз. На рис. 1.5—1.7 приведены диаграммы Эйлера – Венна для двух множеств A è B в случаях, когда A B , A B è A B = . Множеству A B на этих рисунках соответствует заштрихованная часть диаграмм.

Операция «объединение» множеств обладает рядом свойств, напоминающих свойства операции «сложения» чисел. Однако некоторые свойства объединения множеств отличаются от соответствующих свойств сложения чисел.

Åñëè A подмножество множества B, ò.å. A B, òî A B = B (см. рис. 1.6), так как элементы из множества A принадлежат множеству B и второй раз включать их в объединение не надо. Отметим свойства объединения, справедливые для любых множеств A, B è C:

34

A A B è B A B.

Кроме того, из включения A B следует включение A C B C. В частности, для любого множества A имеют место равенства: A A = A

(идемпотентность объединения), а также A = A.

Пример. Пусть A — «множество, состоящее из различных букв русского алфавита, входящих в первую строку “Евгения Онегина”», B — «множество, состоящее из различных букв, входящих во вторую строку

этого романа в стихах». Найдем объединение этих множеств A B.

Множество A состоит из 18 различных букв:

A = {М, О, Й, Д, Я, С, А, Ы, Х, Ч, Е, Т, Н, П, Р, В, И, Л}, а множество B состоит из другой совокупности 13 букв:

B = {К, О, Г, Д, А, Н, Е, В, Ш, У, Т, З, М}. Объединением этих множеств является следующий набор из 23 букв:

A B = {Ì, Î, É, Ä, ß, Ñ, À, Û, Õ, ×, Å, Ò, Í, Ï, Ð, Â, È, Ë, Ê, Ã, Ø, Ó, Ç}.

Поскольку 8 букв М, О, Д, А, Е, Т, Н, В, принадлежащих пересечению множеств A è B, вошли в объединение этих множеств только один раз, то поэтому мы получили только 23 буквы, а не 18 + 13 = 31 букву, т. е. (18 + 13) – 8 = 23.

Замечание. Союз «или» в русском языке может использоваться в двух смыслах: исключающем è неисключающем. В определении объединения множеств союз «или» используется в неисключающем смысле.

В естественном языке союз «или» порою используется как раздели тельная связка: «то или другое, но не оба вместе». Используя союз èëè, мы можем иметь в виду исключающее или. Например, когда мы говорим: «студент сдаст зачет по математике или он не сдаст этот зачет», то, конечно, предполагаем, что он сделает что-то одно. В логике исключающее или используется довольно редко, и мы, за редким исключением, будем обходиться без него. Для хозяев был довольно неожиданным вполне логичный ответ Ходжи Насреддина на вопрос: «Что желаете поесть: плова или бешбармака?» — «А разве у вас всего один котел?» На следующем примере проиллюстрируем еще одну тонкость в определении объединения и пересечения множеств.

Пример. Пусть A — «множество студентов филфака, прогуливающих занятия по высшей математике», B — «множество студентов филфака, надеющихся получить “зачет” по математике». Найдем объединение A B и пересечение A B этих множеств A и B.

35

Напомним, что формально определения для объединения и пересече- ния множеств отличаются только союзами « èëè » è « è », соединяющими условия x A и x B. В формальном определении важную смысловую нагрузку имеет словосочетание «соединяющие условия». Поскольку множества A è B описаны не в виде {x : x обладает свойством Ð}, òî ñîþç « è » без «соединяющих условий» может оказаться двусмысленным. Рассмотрим, например, следующие два множества:

C — «множество студентов филфака, прогуливающих занятия по математике èëè надеющихся получить “зачет” по математике».

D — «множество студентов филфака, прогуливающих занятия по математике è надеющихся получить “зачет” по математике».

Очевидно, что C = A B, но так как в множестве D перечисляются или различные студенты из множеств A è B, или одни и те же студенты из этих множеств, то, по существу, это тоже объединение множеств A è B, ò. å. D = A B. Рассмотрим еще одно множество.

E — «множество студентов филфака, прогуливающих занятия по математике, которые надеются получить “зачет” по математике».

Студенты из множества E принадлежат каждому из множеств A è B, поэтому E = A B.

Соответствующий вывод: При работе с неформально описанными множествами следует пользоваться неформальной, но содержательной частью определений операций над множествами.

Замечание. Выражение «A и B» в естественном языке при перечислении однородных членов часто означает совокупность, в которую вклю- чаются объекты множеств A и B. На математическом языке принадлежность к такой совокупности выражается через A B.

В естественном языке практически все слова многозначны. Смысл слова зачастую невозможно понять, вырвав его из контекста предложения, в которое оно входит. Поэтому при переводе с естественного языка на язык математического формализма нужно пытаться понять смысл переводимого предложения.

Определение разности множеств. Разностью двух множеств A и B, обозначается A \ B (èëè A – B), называется множество, которое состоит из всех элементов, принадлежащих множеству A, но не принадлежащих множеству B:

def

A / B {x : x A è x B}.

В определении разности множеств не предполагается, что множество B является подмножеством множества A. Например, если A è B —

36

«множество студентов филологического факультета, изучающих соответственно английский и немецкий языки», то A \ B — «множество студентов филологического факультета, которые изучают английский язык, но не изучают немецкий язык». Если множество A = {x : x 1} и множество B = {x : x 0}, тогда разность A \ B = {x : 0 x 1}.

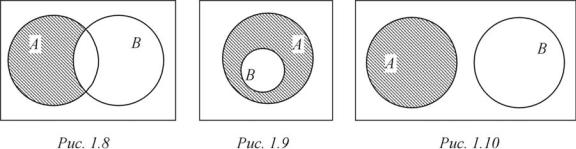
Åñëè A подмножество множества B, ò. å. A B, то тогда A \ B = . На рис. 1.8–1.10 приведены диаграммы Эйлера – Венна для двух множеств A è B в случаях, когда соответственно A B , B A è A B = . Множеству A \ B на этих рисунках соответствует заштрихованная часть диаграмм.

Операция «разность» множеств обладает рядом свойств напоминающих свойства операции «вычитания» или «разности» чисел. Но следует обратить внимание на то, что разность множеств не является операцией,

обратной объединению множеств, которую иногда называют «сложением» множеств. В этом можно убедиться, доказав следующие соотношения (см. для наглядности рис. 1.8—1.10):

(A \ B) B = A B è (A \ B) (A B) = A.

В частности, если B A, òî A B = B и из предыдущего равенства следует, что (A \ B) B = A (см. рис. 1.9). Если множества A è B не пересекают-

ñÿ, ò. å. A B = , òî A \ B = A, поскольку в этом случае множество A не содержит элементов множества B (см. рис. 1.10). Отметим свойство разности, справедливое для любых множеств A, B è C:

A \ B A.

Кроме того, из включения A B следуют включения (A \ C) (B \ C) è (C \ B) (C \ A). В частности, для любого множества A имеют место равенства:

A \ A = , A \ = A è \ A = .

Пример. Пусть A — «множество, состоящее из различных букв русского алфавита, входящих в первую строку “Евгения Онегина”», B — «множество, состоящее из различных букв, входящих во вторую строку этого романа в стихах». Найдем разность этих множеств A \ B.

37

Множество A состоит из 18 различных букв:

A = {М, О, Й, Д, Я, С, А, Ы, Х, Ч, Е, Т, Н, П, Р, В, И, Л}, а множество B состоит из другой совокупности 13 букв:

B = {К, О, Г, Д, А, Н, Е, В, Ш, У, Т, З, М}. Разностью этих множеств вида A \ B является набор из 10 букв:

A \ B = {É, ß, Ñ, Û, Õ, ×, Ï, Ð, È, Ë},

которые принадлежат множеству A, но не содержатся в множестве B. Так как только 8 букв М, О, Д, А, Е, Т, Н, В принадлежат пересечению A B, т. е. содержатся в множестве A и множестве B, то множество A \ B содержит 18 – 8 = 10 букв, а не 18 – 13 = 5 букв.

Замечание. Операция разности множеств «несимметрична» относительно множеств A и B, в том смысле, что

A \ B B \ A, кроме того (A \ B) (B \ A) = .

Например, в предыдущем примере разность A \ B = {Й, Я, С, Ы, Х, Ч, П, Р, И, Л}, а разность B \ A = {К, Г, Ш, У, З}. Убедимся в этом на еще одном примере.

Если в операциях объединения и пересечения оба множества участвуют равноправно, то операция разности, как говорят математики, некоммутативна. Ничего удивительного здесь нет, так как арифметическая разность чисел тоже некоммутативна.

Пример. Пусть A — «множество студентов-филологов, слушавших лекции по курсу “Основы высшей математики”», а B — «множество людей, изучавших медицинскую латынь». Найдем следующие разности мно-

жеств A \ B и B \ A.

Тогда A \ B — «множество студентов-филологов, слушавших лекции по “Основам высшей математики”, но не изучавших медицинскую латынь», а B \ A — «множество людей, изучавших медицинскую латынь, не являющиеся студентами-филологами, которые слушали лекции по “Основам высшей математики”».

Замечание. «Вычитание» из множества A множества B сводится к «удалению» из множества A общей части A и B, т. е. множества A B:

A \ B = A \ (A B).

С такой операцией над множествами мы часто сталкиваемся в реальной жизни. Проанализируем следующий эпизод из работы инспектора

Варнике.

38

Полицейский инспектор Варнике осмотрел сейф, закурил свою трубку и сказал: «Электродрелью вскрывают сейфы только пять взломщиков: Алек Кунце, Фриц Шмидт, Густав Хойгер, Генрих Кунтцман и Томас Мюллер. Но Алек, Фриц и Густав сейчас находятся в тюрьме Моабит. Придется спросить Генриха и Томаса, где они провели прошлую ночь…»

Если обозначить через A — «множество подозреваемых взломщиков, пользующихся электродрелью», а через B — «множество подозреваемых, находившихся в тюрьме Моабит», то, удалив из множества A все элементы множества B, инспектор Варнике сузил круг подозреваемых в ограблении преступников. Его метод рассуждения основан на применении операции разности множеств.

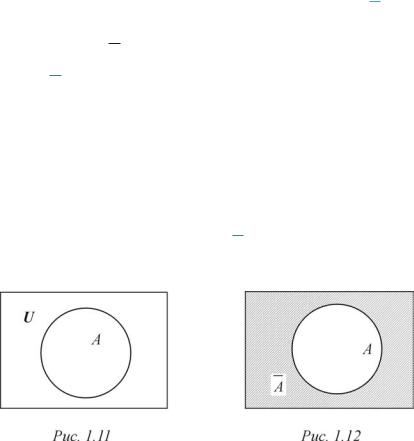
Определение дополнения множеств. Если обозначить через U —

универсальное множество, содержащее множество A, то разность U \ A

называется дополнением множества A и обозначается A:

def

A {x : x U è x A}.

Дополнение A множества A — это множество элементов фиксированного универсального множества U, не входящих в A. Например, если U — множество всех действительных чисел R, то дополнением множества всех

рациональных чисел в множестве действительных чисел будет множество всех иррациональных чисел.

Напомним, что при графической иллюстрации универсальное множество представляется обычно прямоугольником на плоскости, а множества — кругами, лежащими внутри этого прямоугольника (рис. 1.11). На рис. 1.12 дополнению множества A, ò. å. A, соответствует заштрихованная часть этого прямоугольника.

Чтобы избежать трудностей при изображении дополнения множества будем следовать правилу Джона Венна: «Не следует стараться

заштриховать всю внешнюю часть диаграммы». Тем более что в реальных ситуациях дополнение может оказаться не таким уж «большим» множеством.

39

Например, Марина Цветаева â «Записных книжках» писала: «Меня презирают — (и в праве презирать) — все.

Служащие — за то, что не служу, писатели — за то, что не печатаю, прислуга — за то, что не барыня, барыни — за то, что в мужицких сапогах (прислуги и барыни!).

Кроме того — все — за безденежье.

1/4 презирают, 1/4 презирает и жалеет, 1/2 — жалеет. (1/2 + 1/4 + 1/4 = 1)

А то, что уже вне единицы — Поэты! — восторгаются».

Заметим, что такая операция, как дополнение, отсутствует в обыч- ной алгебре. Вообще говоря, в теории множеств дополнений у множеств тоже нет, но о них тем не менее говорят, имея в виду дополнение до фиксированного подразумеваемого множества U.

Отметим следующие свойства дополнения, справедливые для любого множества A, и содержащего его универсального множества U:

A A = U è A A = .

Кроме того, дополнение пустого множества совпадает с универсальным множеством, а дополнение универсального множества — с пустым множеством.

Пример. Пусть A — «множество, состоящее из различных букв русского алфавита, входящих в первую строку “Евгения Онегина”», а универсальное множество U — «множество всех букв русского алфавита».

Найдем дополнение множества A, т. е. множество A = U \ A.

Множество A состоит из 18 различных букв русского алфавита: A = {Ì, Î, É, Ä, ß, Ñ, À, Û, Õ, ×, Å, Ò, Í, Ï, Ð, Â, È, Ë}.

Поскольку в русском алфавите 33 буквы, то дополнением является следующее множество, состоящее из 15 букв:

A = {Á, Ã, ¨, Æ, Ç, Ê, Ó, Ô, Ö, Ø, Ù, Ú, Ü, Ý, Þ}.

Замечание. Для разности произвольных множеств A и B справедливо следующее равенство:

A \ B = A B,

т. е. разность множеств A \ B есть пересечение множества A и дополне-

ния множества B.

С помощью понятия «дополнение» и имеющихся у нас понятий «подмножество» и «пересечение подмножеств» дадим на языке теории множеств формальное определение хорошего поступка. Будем считать, что

«хороший поступок — это такой поступок, который приносит добро хотя бы некоторым людям и не приносит зла никому».

40

Пусть универсальным множеством U будет множество всех поступков. Обозначим через A — «множество хороших поступков», B — «множество поступков, приносящих добро хотя бы одному человеку», а через C — «множество поступков, приносящих зло хотя бы одному человеку». Тогда математической формулой данного выше определения хорошего поступка будет соотношение:

A B \ C .

Замечание. Чем «больше» само множество, тем «меньше» элементов остается в его дополнении, т. е.

A B B A.

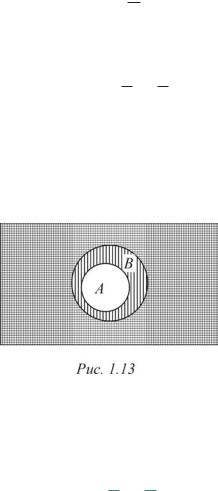
Для понимания этого утверждения воспользуемся следующей графи- ческой иллюстрацией диаграммы Эйлера – Венна. На рис. 1.13 универсальное множество U изображено в виде прямоугольника, а множества A è B в виде кругов, где A B.

Дополнение к множеству A состоит из точек прямоугольника, лежащих вне меньшего круга (обозначено вертикальной штриховкой), а дополнение к множеству B состоит из точек прямоугольника, лежащих вне большего круга (обозначено горизонтальной штриховкой). ßñíî, ÷òî äëÿ ýòèõ

дополнений справедливо включение B A.

Определение симметрической разности множеств. Симметриче- ской разностью двух множеств A и B, обозначается A B, называется множество, которое состоит из всех элементов, принадлежащих ровно одному из множеств A и B:

def

A B (A \ B) (B \ A).

Например, если A è B — «множество студентов филологического факультета, изучающих соответственно английский и немецкий языки», то A B — «множество студентов филологического факультета, которые изуча- ют английский, но не изучают немецкий язык, или изучают немецкий язык,

41