Рекомендации к решению заданий

1. Найдем частное решение дифференциального уравнения удовлетворяющее начальному условию у(0)=0.

Заданное уравнение является линейным. Полагаем и Подставим в исходное уравнение, получим

(1)

Подберем функцию так, чтобы выражение, содержащиеся в скобках, обращалось в нуль:

После интегрирования получим При равенство (1) обратится в уравнение

Общее решение исходного уравнения будет или . Используя начальные условия, вычислим соответствующее ему значение постоянной С: .

Тогда частное решение имеет вид у=sin x.

2. Найдем частные решения линейных однородных уравнений второго порядка:

a) ;

б) ;

в) .

a) составим характеристическое уравнение Корни этого уравнения поэтому общее решение записывается в виде . Чтобы получить частное решение, необходимо подставить начальные данные в выражение для Получим , откуда следовательно, искомое решение будет иметь вид ;

б) cоставим характеристическое уравнение к²–2к+1=0. Оно имеет два равных корня к₁=к₂=1, тогда общее решение записывается в виде у=с₁ е^х+с₂хе^х, откуда . Учитывая начальные условия, получим откуда с₂=1. Искомое частное решение будет иметь вид у =е^х+хе^х;

в) cоставим характеристическое уравнение к²+4к +13=0. Это уравнение не имеет вещественных корней. Тогда общее решение записывается в виде .

В нашем случае т. е. .

Для нахождения частного решения дифференциального уравнения вычислим первую и вторую производные от найденного общего решения: .

Воспользовавшись заданными начальными условиями, получим:

откуда с₁ = 0, .

Частное решение будет иметь вид .

Задание 13

Задачи 241–260. Найти: а) частное решение дифференциального уравнения первого порядка; б) частное решение линейного однородного уравнения второго порядка.

241. ; .	; .
242. ; .	.
243. ; .	.
244. ; .	.
245. .	.
246. ; .	.
247. а) .	.
248. .	.
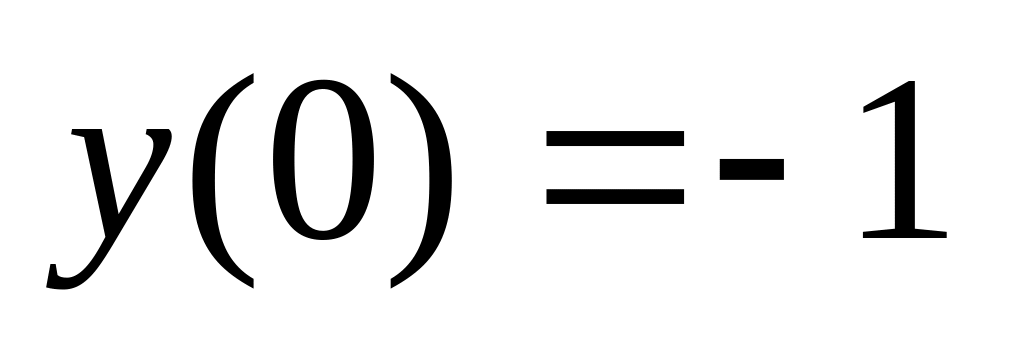249.	.
250. ; .	.
251.	.
252.	.
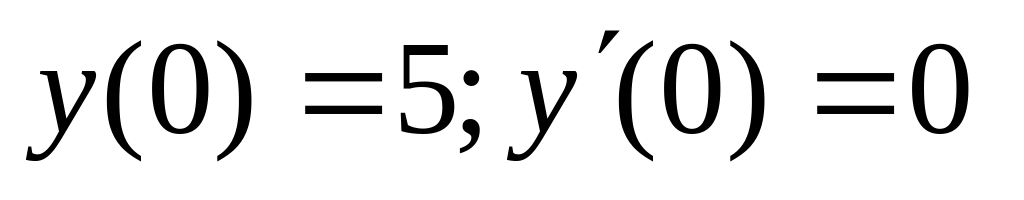253.	.
254.	.
255.	.
256.	.
257. .	.
258.	.
259.
260.