69

замкнутые ломаные незамкнутые ломаные

Простые ломаные

Рис. 61

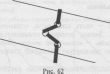
полнении такого задания: «Имеются модели реки, островков, мос­тиков. Нужно помочь зайчику перебраться на другой берег» (рис. 62).

Обычно дети трех-четырех лет легко выделяют круг среди других фигур и правильно его называют. Дошкольники характеризуют круг в сравнении с многоугольником: «У круга нет углов, нет сторон». Окружность называют «границей круга», а центр — «серединой кру­га».

Круг — это фигура, состоящая из всех точек плоскости, расстоя­ние от которых до данной точки не больше заданного. Данная точка О называется центром круга, а заданное расстояние R — радиусом круга (рис. 63).

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Круг можно определить как фигуру, состоящую из окружности и ее внутренней области.

Окружность — это множество точек плоскости, равноудаленных от заданной точки. Данная точка О называется центром окружнос­ти, а заданное расстояние R — ее радиусом (рис. 64).

В детском саду дети также знакомятся с овалом («фигурой, похо­жей на круг тем, что у нее нет углов и сторон, но отличающейся от круга своей вытянутостью»), В геометрии такой термин не рассмат­ривается, но изучается эллипс. Его нецелесообразно предлагать де­тям из-за сложности построения. Так как в быту часто используют слова «овал», «предмет овальной формы», знания об овале необхо­димы детям как элемент сенсорного воспитания и речевого раз­вития.

4. Многоугольники

Многоугольник - часть плоскости, ограниченная простой за­мкнутой ломаной. Звенья ломаной называются сторонами много­угольника, а вершины — вершинами многоугольника. Границу много­угольника (простую замкнутую ломаную) также называют многоу­гольником.

В работе с дошкольниками обычно рассматриваются модели фигур из картона, пластмассы или дерева, предлагаются задания по рисованию многоугольников при помощи трафаретов и обводок, за­крашиванию фигур. В процессе этой деятельности дети знакомятся с названиями фигур, их структурой и некоторыми свойствами, ис­пользуют такие термины, как: граница фигуры, внутренняя область фигуры и др.

Выпуклый многоугольник лежит в одной полуплоскости от­носительно любой прямой, содержащей его сторону (рис. 65).

выпуклый .многоугольник нсвыпуклый многоугольник

71

Рис. 66

Дети в своей деятельности сталкиваются как с выпуклыми, так и с невыпуклыми многоугольниками (рис. 66):

Правильный многоугольник — выпуклый многоугольник, у кото­рого все стороны равны и все углы равны.

Например: правильный треугольник — это равносторонний тре­угольник, правильный четырехугольник — это квадрат.

Задание 39

1. Какие из многоугольников, изображенных на рисунке 66, явля­ются выпуклыми?

2. Определите объем понятия «правильный многоугольник».

ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Многоугольники классифицируются по числу сторон или углов: треугольники (рис. 67), четырехугольники (рис. 68), пятиугольники (рис. 69) и т.д.

Задание 40

1. Какой геометрической фигурой является:

• вершина многоугольника,

• сторона многоугольника,

• вершина угла,

• сторона угла.

2. Назовите известные вам виды многоугольников, изображенных на рисунках 65, 66, 67.

Дошкольники, знакомясь с треугольником, квадратом и други­ми многоугольниками, учатся показывать и считать их углы и сто­роны.

Например, при знакомстве с треугольником может происходить такая беседа:

• Как называется эта фигура? — Треугольник.

• Почему она так называется? - У нее 3 угла.

• Что еще есть у треугольника? — Стороны.

• Сколько сторон? — 3 стороны.

Вывод: «Треугольник — это фигура, у которой 3 стороны и 3 угла».

Это, конечно, не математическое определение треугольника, а описание его свойств.

Треугольник — это многоугольник, у которого 3 угла.

Равносторонний треугольник — треугольник, у которого все сто­роны равны.

Равнобедренный треугольник — треугольник, у которого две сто­роны равны.

Задание 41

Дайте определения остроугольного, тупоугольного и прямоуголь­ного треугольников.

С остроугольным, тупоугольным, прямоугольным треугольниками можно знакомить детей только после изучения видов углов. С гра­